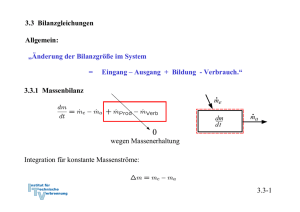
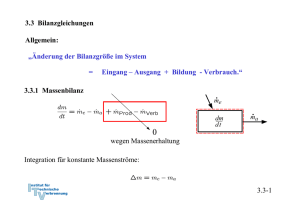
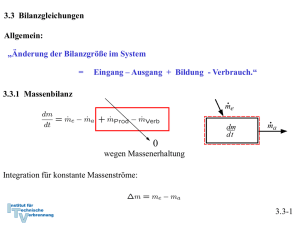
4.1.1 Energie und Arbeit Arbeit einer Kraft Die auf dem Weg von 1

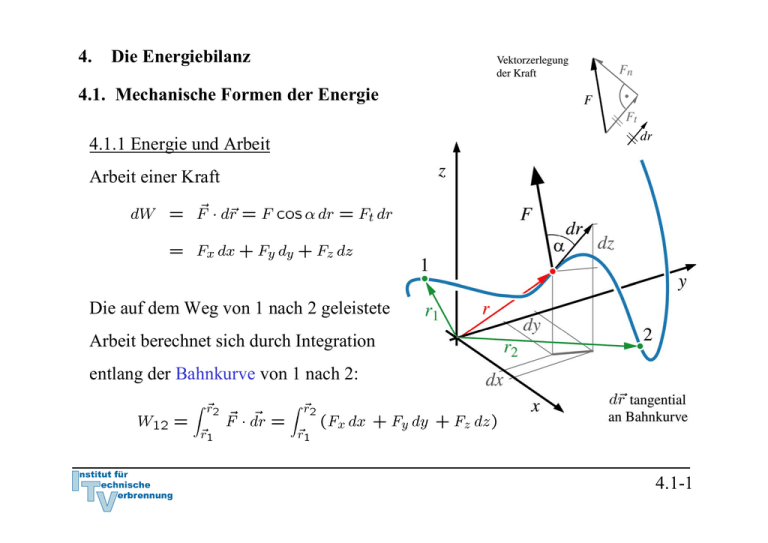
4.
Die Energiebilanz
4.1. Mechanische Formen der Energie
4.1.1 Energie und Arbeit
Arbeit einer Kraft
Die auf dem Weg von 1 nach 2 geleistete
Arbeit berechnet sich durch Integration
entlang der Bahnkurve von 1 nach 2:
4.1-1
Wenn das angegebene Koordinatensystem ein Inertialsystem ist, sind nach Newton
Beschleunigung und Kraft verknüpft:
Definition Geschwindigkeit:
Definition Beschleunigung:
Es gilt mit der Kettenregel:
Arbeit der Kraft:
Dies ist der Arbeitssatz oder Energiesatz der Mechanik.
4.1-2
Definition kinetische Energie:
Damit ist nach dem Arbeitssatz der Mechanik die Arbeit der Kraft mit der Änderung
der kinetischen Energie des Massenpunktes verknüpft:
4.1-3
Beispiel: Bremsweg eines PKW bei konstanter Bremskraft
(68iger Modell, Bremsen vorne kaputt)
Die Arbeit der Bremskraft erwirkt eine Änderung der kinetischen Energie
Befreiung des Systems PKW
Bremsweg
4.1-4
Spezialfall:
Arbeit der Gewichtskraft eines Massenpunktes bei
Lageveränderung im Schwerefeld der Erde
Falls z2 > z1 ist die vom System (Masse m)
geleistete Arbeit negativ:
Dies entspricht der auch in der Thermodynamik üblichen Vorzeichenkonvention, dass einem
System zugeführte Arbeiten positiv, abgegebene Arbeiten dagegen negativ bewertet werden.
4.1-5
Definition:
Potentielle Energie
(Energie der Lage, die im System gespeichert)
Wir erhalten damit:
Falls z2 > z1 hat das System (Masse m) Arbeit gegen die Gewichtskraft geleistet, also
Arbeit abgegeben. Nach dem Arbeitssatz muss dies einer Abnahme der kinetischen
Energie des Systems entsprechen:
4.1-6
Die in einem einfachen mechanischen System insgesamt gespeicherten Energie
setzt sich nach den getroffenen Definitionen aus der potentiellen und der
kinetischen Energie zusammen:
Offensichtlich bleibt ohne die Arbeit weiterer äußerer Kräfte die gesamte
mechanische Energie aus kinetischer und potentieller Energie konstant.
Dies ist die Aussage des Energieerhaltungssatzes.
4.1-7
Beispiel: Pendelversuch von Galilei
Zustand 0:
Zustand 1:
Fadenkraft leistet keine Arbeit am System, da
sie stets senkrecht auf der Bahnkurve steht
⇒ Energieerhaltung:
Zustand 2:
Freischnitt des Systems
in allgemeiner Lage
Eine Kenntnis der Zwischenzustände ist nicht nötig!
4.1-8
Der Arbeitssatz der Mechanik kann auch für ein thermodynamisches System
angewandt werden.
Wir müssen dazu jedoch voraussetzen, dass keine anderen inneren Energien des
Systems in kinetische und potentielle Energie umgesetzt werden.
Am System sollen neben der Gewichtskraft
andere äußere Kräfte angreifen.
Der Arbeitssatz liefert:
4.1-9
Reibung
Makroskopische Bewegungen sind immer mit Reibungsverlusten verbunden. Die
Reibungsarbeit
wird in Wärme umgewandelt. Die Wärme steht dann nicht mehr
unmittelbar als mechanische Energie zur Verfügung.
Siehe Folie 4.1-9 mit der Reibkraft als äußerer Kraft:
Da die Reibkraft der Bewegung immer entgegen gerichtet ist, ergibt das Integral
einen negativen Wert
oder
4.1-10
Potentielle Energie und mechanisches Gleichgewicht
Ein Körper ist im Gleichgewicht, wenn er seinen Bewegungszustand nicht mehr ändert.
Alle an ihm angreifenden Kräfte und Momente müssen dann in der Summe
verschwinden.
Aus der Erfahrung:
Die Kugel kann an der Position 1 nicht
in Ruhe verharren, wohl aber in Position
2 → stabiler Gleichgewichtszustand.
Da die Bahnkurve auch gleichzeitig den
Verlauf der potentiellen Energie darstellt,
kann das Auftreten eines lokalen
Minimums der potentiellen Energie als
Bedingung für das stabile Gleichgewicht abgelesen werden.
Darüberhinaus unterscheidet man noch labiles (3) und indifferentes
Gleichgewicht (4). In jedem Fall verschwindet die Ableitung:
4.1-11
Dem stabilen Gleichgewicht (1) kommt gegenüber den anderen Gleichgewichtslagen
eine Sonderstellung zu:
Wird das System in den Position 3 gestört, so gelangt es in instabile Zustände und die
Störung wird verstärkt → labiles Gleichgewicht.
Nach der Störung sich selbst überlassen, wird der Körper freiwillig in eine stabile
Lage übergehen.
In Position 4 wird die Störung, wenn von Reibung abgesehen wird, nicht gedämpft
oder verstärkt → indifferentes Gleichgewicht.
Es ist nun die wesentliche Aufgabe der Thermodynamik, Gleichgewichte und
Stabilitätsaussagen wie dEpot/dx = 0 abzuleiten, bei denen nicht nur mechanische
Energieformen und einfache Körper sondern alle Energieformen und ganze Systeme
betrachtet werden (vergl. Kapitel 8).
4.1-12
Wir haben die Arbeit äußerer Kräfte
bereits auf ein thermodynamisches System statt auf einen einfachen Massenpunkt
angewandt.
Wir konnten die Arbeit äußerer Kräfte für die Änderung von kinetischer und
potentieller Energie des Systems verantwortlich machen, die deshalb auch als
äußere Energien bezeichnet werden.
Der Zusammenhang ist korrekt, solange die Kräfte nicht auch Änderungen des
inneren Zustands des Systems bewirken oder sich der innere Zustand des Systems
selbst ändert .
Dies ist bei thermodynamischen Systemen jedoch typischerweise der Fall und
erfordert eine Verallgemeinerung des Energiesatzes der Mechanik.
4.1-13
Schon etwas komplexere mechanische Systeme können solche inneren
Zustandsänderungen aufweisen.
Ein Beispiel:
Mechanisches System aus Rad, Wagenkasten
und vorgespannter Feder.
Start (Zustand 1) aus der Ruhe auf
horizontalem Untergrund.
Arbeitssatz:
4.1-14
Festlegung des Systems und Freischnitt
Arbeiten äußerer Kräfte beim
verlustlosen Rollen der Räder:
Energien zu den verschiedenen Zeitpunkten:
Kinetische Energie zum Zeitpunkt 2 durch
Entspannen der Feder:
Bem.: Diese kinetische Energie setzt sich zusammen aus der Rotationsenergie der Räder und der Translationsenergie
von Rädern und Wagenkasten.
4.1-15
Wir werden im Abschnitt 4.2 sehen, dass äußere Kräfte auch den inneren Zustand eines
Systems verändern können, nämlich schon dann, wenn die Abmessungen des Systems
durch diese Kräfte verändert werden.
Das wird im Abschnitt 4.2 mit der Volumenänderungsarbeit (vergl. 4.2-9) eingeführt.
Umgekehrt kann die Änderung des inneren Zustands des Systems auch auf die
Änderung äußerer Energien des Systems Einfluss nehmen. Dies geschieht zum Beispiel
bei Fahrzeugen. Hier wird durch Verbrennung von Kraftstoff oder Umwandlung
gespeicherter elektrischer Energie ein Teil der im System gespeicherten Energie in
Bewegungsenergie und Energie der Lage umgewandelt.
Die Einbeziehung aller möglicher Energieformen und -wandlungen in den
Energieerhaltungssatz wird durch den 1. Hauptsatz der Thermodynamik geleistet.
4.1-16
4.2 Erster Hauptsatz der Thermodynamik
„Die Gesamtenergie E eines Systems ändert sich durch Zu- und Abfuhr von
Energie über die Systemgrenzen.“
Im Folgenden: Spezifizierung der verschiedenen Energieströme.
Dabei werden wir uns auf die wichtigsten Energieformen beschränken.*)
*)
Vorzeichenregelung: zugeführte Energien werden positiv bewertet
4.2-1
4.2.1 Gesamtenergie oder Energieinhalt eines Systems
Die Gesamtenergie E eines thermodynamischen Systems setzt sich zusammen aus den
äußeren Energien Ea bestehend aus
kinetischer Energie des Systems Ekin
und potentieller Energie des Systems Epot
und der im System gespeicherten Energie U, der inneren Energie
Es lassen sich wieder molare und spezifische Größen formulieren:
Gesamtenergie:
Innere Energie:
4.2-2
Die innere Energie U
Wie der Druck, das Volumen und die Temperatur ist auch die innere Energie
eine Zustandsgröße. Es besteht deshalb z. B. der funktionale Zusammenhang
Eine solche Beziehung heißt kalorische Zustandsgleichung. Die innere Energie
ist eine Zustandsgröße.
Über die thermische Zustandsgleichung
sind Volumen, Druck und
Temperatur voneinander abhängig, so dass die innere Energie auch wahlweise
als Funktion der anderen Zustandsgrößen geschrieben werden kann.
4.2-3
Da die innere Energie eine Zustandsfunktion ist, besitzt sie ein vollständiges
Differential.
Falls die innere Energie als Funktion der
Temperatur und des spezifischen
Volumens gegeben ist
lautet das vollständige Differential:
oder:
4.2-4
Spezialfall: Die kalorische Zustandsgleichung des idealen Gases
Beim idealen Gas beschreibt die innere Energie die thermische Energie
des Systems auf Grund der Bewegung von Molekülen (Billardkugelmodell).
Innere Energie
Molare innere Energie
.
Für ein einatomiges, ideales Gas hatten wir
gefunden:
Es folgt für die molare innere Energie
und für die spezifische innere Energie:
Für ein ideales Gas ist daher die innere Energie nur eine Funktion der Temperatur.
4.2-5
Die äußeren Energien Ea
Die kinetischen und potentiellen Energien beziehen sich auf die Bewegung des
Systems als Ganzes relativ zu einem festen Bezugssystem (vergl. 4.1-5).
Sie spielen bei geschlossenen Systemen, da diese meist ortsfest sind, oft keine Rolle.
Zudem können vielfach alleine die Arbeiten äußerer Kräfte, für deren Änderung
verantwortlich gemacht werden.
Die Bilanz
kann deshalb oft von der Energiebilanz für das System abgespalten werden (vergl. die
Bemerkung auf Folien 4.1-11 und 4.1-12).
Diese Möglichkeit besteht jedoch nicht immer, so dass eine genaue Betrachtung im
Einzelfall notwendig ist.
4.2-6
4.2.2 Verschiedene Arbeitsformen
Exemplarisch ohne Anspruch auf Vollständigkeit seien aufgezählt:
-
Arbeit äußerer Kräfte bei festen Systemgrenzen
Wir können uns hier auf die Vorüberlegungen zu den mechanische Energieformen
beziehen (vergl. 4.1-5).
Alle Kräfte, die von außen auf das System einwirken, wollen wir
als äußere Kräfte bezeichnen.
Durch diese Kräfte ändern sich kinetische und potentielle
Energien des Systems als Ganzes.
Die Arbeit der Gewichtskraft ist für die Änderung der potentiellen Energie maßgeblich:
4.2-7
- elektrische Arbeit
Zum Beispiel durch Zufuhr elektrischer Energie an Motor M aus der Umgebung
Wel > 0 oder Abgabe an ein Leitungsnetz außerhalb des Systems erzeugt durch
einen Generator G innerhalb des Systems Wel < 0.
4.2-8
- Wellenarbeit
Übertragen durch eine über die Systemgrenze ragende Welle
Eine Welle, angetrieben von einem außerhalb des Systems stehenden Motor M, wird
Arbeit ins System einspeisen W > 0.
Eine Welle, die einen Generator G außerhalb des Systems antreibt, entzieht dem
System Arbeit W < 0.
Durch die Welle eines Rührwerks wird von außen Arbeit in das System Welle
übertragen W > 0.
Bei den bisherigen Beispielen sind feste Systemgrenzen angenommen worden.
Im Folgenden: Geschlossene Systemen mit bewegten Systemgrenzen
4.2-9
Volumenänderungsarbeit (Verschiebearbeit) und Nutzarbeit
Betrachtet wird exemplarisch ein System aus
Zylinder und Kolben. Die Kraft an der Kolbenstange
leistet die Arbeit
Bei quasistatischer, reversibler Zustandsänderung
durchläuft das System eine Reihe von Gleichgewichtszuständen.
Die träge Masse des Kolbens spielt dann keine Rolle.
Eine Kräftebilanz am Kolben liefert deshalb
für die Kraft:
4.2-10
Nutzarbeit und Volumenänderungsarbeit
Die an die Kolbenstange abgeführte Arbeit, die
Nutzarbeit, bei quasistatischer, reversibler
Zustandsänderung ist daher:
Der erste Term ist die Volumenänderungsarbeit des im
Zylinder eingeschlossenen Gases:
oder da m=const:
Die Volumenänderungsarbeit des eingeschlossenen Gases wird bei Volumenvergrößerung von diesem an die Umgebung abgegeben:
4.2-11
Verschiebearbeit
Der zweite Term ist die von der Umgebung
aufgenommene Verschiebearbeit
Sie entspricht der Volumenänderungsarbeit der
Umgebung, wenn, wie in der Skizze angedeutet, die
Umgebung als Bilanzsystems herangezogen wird.
Die Verschiebearbeit ist also die Volumenänderungsarbeit gegen einen konstanten
Druck. Der Begriff tritt bei vom Fluid durchströmten Systemen, also offenen Systemen,
nochmals in Erscheinung (vgl. 4.2-14).
Die Nutzarbeit ist nur ein Teil der vom System abgegebenen Arbeit.
Ein Anteil der vom Gas abgegebenenVolumenänderungsarbeit wird als
Verschiebearbeit an die Umgebung übergeben und kann nicht genutzt werden.
4.2-12
Volumenänderungsarbeit als reversible Arbeit
Die gegebene Definition zur Volumenänderungsarbeit zeigt, dass sich die
Volumenänderungsarbeit durch Umkehrung der Kolbenbewegung vollständig
zurückgewinnen lässt.
Solche Vorgänge werden als verlustlos oder reversibel bezeichnet.
Die Volumenänderungsarbeit ist also eine reversible Arbeit.
Die Umkehrbarkeit des Kompressionsprozesses für das System „Gas“ setzt voraus,
dass keine Verwirbelung durch innere Reibung im Gas auftritt.
Die Kolbenbewegung muss dazu sehr langsam, eigentlich unendlich langsam
erfolgen. Es besteht zu jedem Zeitpunkt mechanisches Gleichgewicht.
Bemerkung: Der Verluste durch Reibung zwischen Kolben und Wand spielt für das System „Gas“
keine Rolle. Der Kolben gehört ja gar nicht zum System! Erst bei der Betrachtung der Nutzarbeit am
System „Kolben“ macht diese Reibung ihren Einfluss geltend und verringert die erzielbare Nutzarbeit.
Der Terminus „reibungsfreier Kolben“ meint oft lax die Vernachlässigung aller Verluste.
4.2-13
Volumenänderungsarbeit pro Zeiteinheit
beim Ein- und Ausschieben einer Masse
Geschlossenes System mit mitbewegten Grenzen wird zu zwei Zeitpunkten 1 und 2
im Abstand dt (gedachte Kolben am Ein und Austritt) betrachtet.
Volumenänderungsarbeit während des Zeitintervalls dt im Eintritt,
Kraft F1 = p1 A , Wegänderung dx = c dt :
Volumenänderungsarbeit pro Zeiteinheit im Eintritt:
4.2-14
Die im geschlossenen System enthaltene Masse bleibt konstant.
Deshalb sind die Massenströme am Ein- und Austritt gleich und die
Massenstromdichten ρ c gekoppelt:
Volumenänderungsarbeit oder Verschiebearbeiten pro Zeiteinheit im Eintritt:
und am Austritt:
Summe der Verschiebearbeiten pro Zeiteinheit zwischen Ein- und Austritt:
4.2-15
Übergang vom geschlossenen System zum offenen Kontrollraum
Die am geschlossenen System abgeleiteten Verschiebearbeiten pro Zeiteinheit
können als Arbeitsströme gedeutet werden, die zu jedem Zeitpunkt einem System
mit durchströmter Bilanzhülle (Kontrollraum), dem offenen System , zu- bzw.
abgeführt werden.
Diese Arbeitsströme sind an die Massenströme, welche die Kontrollgrenzen
überschreiten, gekoppelt.
Die spezifischeVerschiebearbeit ist durch gegeben.
4.2-16
Ergebnis:
Die ein- und austretenden Massenströme
führen mit:
- Kinetische und potentielle Energien,
- Innere Energien,
- Verschiebearbeiten
Die eintretenden Energieströme liefern an das System
die Energie
die austretenden Ströme entfernen den Energiestrom
4.2-17
Die Enthalpie H
Wir definieren die Summe aus innerer Energie U und Verschiebearbeit pV als neue
Größe:
Die molaren und spezifischen Größen lauten:
Wie die innere Energie ist auch die Enthalpie eine Zustandsgröße:
Sie besitzt deshalb wie diese ein vollständiges Differential (vergl. 4.2-4):
4.2-18
Spezialfall: ideales Gas (vergl. 4.2-5)
Aus
folgt mit der thermischen Zustandsgleichung des idealen Gases
und der inneren Energie
sofort, dass auch die Enthalpie beim idealen Gas nur eine Funktion der Temperatur
ist:
Entsprechend gilt für die spezifischen Größen:
4.2-19
Totalenthalpie
Als Summe aus Enthalpie und kinetischer und potentieller Energie wird auch
die Totalenthalpie eingeführt:
Für die molaren und spezifischen Größen gilt:
Entsprechend wird die Energiebilanz am
Kontrollvolumen noch kompakter
darstellbar:
4.2-20
4.2.3 Wärmeströme
Physikalische Deutung des Wärmestroms über Wände ins Bilanzsystem
Wärmestrom
J/s , 1 J = 1 Nm
Wärmeleitung (Fouriersches Gesetz) ,
z. B. in der ebenen Wand
Wärmeleitfähigkeit: λ
[λ] = J/(msK)
4.2-21
Wärmestrom bei Konvektion
Wärmeübertragung
Wärmeübergangskoeffizient α
[α] = J/(m2sK)
Temperaturprofil T(r) wird durch die mittlere Temperatur Tm ersetzt,
α wird empirisch für verschiedene Strömungen bestimmt.
4.2-22
Wärmetransport und Irreversibilität
Die vorgenannten Prozesse der Wärmeübertragung haben, wie die Erfahrung lehrt,
eine eindeutige, vorgegebene Richtung.
Wärme fließt stets vom heißeren zum kälteren Körper. Zwischen dem thermodynamischen System und der Umgebung wird es zu einem Temperaturausgleich kommen.
Die dargestellten Prozesse der Wärmeleitung und Konvektion sind also nicht
umkehrbar oder irreversibel.
4.2-23
Reversibler Wärmetransport
Dieser Begriff erscheint nach der vorstehenden Bemerkung sinnlos. Wir werden aber
sehen, dass er für theoretische Konzepte eine wichtige Rolle spielt.
Reversibler Wärmetransport erfordert eine verschwindende Temperaturdifferenz ΔT
zwischen System und Umgebung. Der Wärmestrom tendiert mit ΔT → 0 selbst gegen
Null. Damit geht aber ein unendlich langsamer Temperaturausgleich einher.
Sind praktisch keine Temperaturunterschiede vorhanden, ist der Wärmefluss im
Prinzip umkehrbar.
System und Umgebung sind bei der reversiblen Wärmezufuhr zu jedem Zeitpunkt im
thermischen Gleichgewicht.
(Vergl. auch die Bemerkung zur reversiblen Arbeit Folie 4.2-11)
Wir werden bei der späteren Quantifizierung von Irreversibilitäten darauf geführt, dass
das Maß für die Irreversibilitäten proportional zu ΔT 2 ist und damit von höherer
Ordnung gegen Null tendiert als der Wärmestrom (Abschnitt 5).
4.2-24
Erster Hauptsatz der Thermodynamik
Damit können wir die Energiebilanz endgültig formulieren:
„Die Gesamtenergie eines Systems ändert sich durch die mit den
Massenströmen über die Systemgrenzen transportierte Totalenthalpien und
durch Arbeits- und Wärmeströme über die Systemgrenzen.“
4.2-25
4.3 Verschiedene Formen des 1. Hauptsatzes
4.3.1 Geschlossenes System ohne Änderung äußerer Energien
Keine Massenflüsse über Systemgrenze, m = const,
Keine Änderung von kinetischen und potentiellen Energien des Systems
⇒ Die Änderung der inneren Energie wird betrachtet: e = u.
Abstraktion und Freischnitt:
4.3-1
Erster Hauptsatz:
mit
Volumenänderungsarbeit:
(reversibel)
Reibungsarbeit:
(irreversibel)
4.3-2
Der während eines Zeitintervalls 1-2 zugeführte spezifische Wärmestrom wird als
bezeichnet
(analog für die Volumenänderungsarbeit und die Reibungsarbeit)
Da die innere Energie eine Zustandsfunktion ist, braucht nur die Änderung der inneren
Energie zwischen den Zeitpunkten
betrachtet zu werden.
1. Hauptsatz für geschlossene Systeme in differentieller und integraler Form
Die Änderung der inneren Energie eines geschlossenen Systems ist gleich der
Summe aus Wärme, die über die Systemgrenze zugeführt wird, der
Volumenänderungsarbeit des Systems und aller irreversibel zugeführten Arbeiten.
4.3-3
Im Allgemeinen können sich auch die äußeren Energien des Systems ändern
und äußere Kräfte
Arbeit leisten.
Sind diese Energieformen zu berücksichtigen lautet der 1. Hauptsatz in differentieller
Form
und in integraler Form
4.3-4
Spezialfall:
1. Hauptsatz für geschlossene Systeme bei reversibler Prozessführung
keine mechanischen Verluste und Wärmezufuhr reversibel
(vergl. die Bemerkungen auf Seite 4.2-13 und 4.2-22)
4.3-5
Beispiel: Kolben-Zylindersystem im Schwerefeld der Erde
Ein Kolben mit Masse mK schließt einen mit Gas,
Masse mG, gefüllten Zylinder nach oben ab.
Der Kolben werde ein kleines Stück dz langsam nach oben
bewegt, so dass das Gas im Inneren stets im Gleichgewicht
sei. Der Kolben gleite ferner reibungsfrei.
Formulieren Sie die differenzielle Energiebilanz für diesen
Prozess!
Der 1. Hauptsatz für ein geschlossenes System mit Änderung
äußerer Energien lautet:
4.3-6
Nebenstehend sind zwei mögliche Systemabgrenzungen
skizziert.
Für beide Systeme sollen die Bilanzen formuliert werden.
Da beide Systeme bei dem als langsam angenommenen
Vorgang stets im Gleichgewicht stehen und auch der
Kolben reibungsfrei gleitet, kann die Reibarbeit δwR in
beiden Fällen vernachlässigt werden.
Die Systeme besitzt ebenfalls keine kinetische Energie.
4.3-7
Die Bilanz lautet unter diesen Voraussetzungen für beide Systeme:
System 1:
Bei Verschiebung der oberen Grenze gewinnt das Gas die
potentielle Energie:
Die Volumenänderungsarbeit ist:
Die Arbeit der äußeren Kräfte verschwindet, da die Differenz der
Druckkräfte der Gewichtskraft des Gases das Gleichgewicht hält
(Hydrostatik).
Die resultierende äußere Kraft also verschwindet:
Die Bilanz für System 1 lautet also:
4.3-8
System 2:
Bei Verschiebung der oberen Grenze gewinnen das Gas und der
Kolben die potentielle Energie:
Die Volumenänderungsarbeit ist Verschiebearbeit gegen die
Umgebung:
Die resultierende äußere Kraft
leistet die Arbeit:
Die Bilanz für System 2 lautet also:
Wegen der hydrostatischen Aussage
folgt wieder wie für System 1:
4.3-9
4.3.2 Stationärer Fließprozess in offenen Systemen
Annahmen:
1.
Stationär → Masse im System konstant:
2.
Arbeit ist die dem System durch Wellen übertragene Arbeit:
4.3-10
Bilanz am stationären offenen System:
Zugeführter Wärmestrom:
Zugeführte Leistung:
4.3-11
Mit der Enthalpie
folgt der 1. Hauptsatz für stationären Fließprozess
Die Summe aus zugeführter Wärme und zugeführter technischer Arbeit ist
gleich der Änderung der Enthalpie, der kinetischen und der potentiellen
Energie des Mediums, das in einem stationären Fließprozess durch einen
Kontrollraum strömt.
4.3-12
Vergleich mit 1. Hauptsatz für geschlossene Systeme
Die Bilanz am offenen System lautet:
Für das mitschwimmende Massenelement (grün), das
bei 1 ein- und bei 2 austritt, liefert der 1. Hauptsatz für
das geschlossene System
mit
Die Differenz der beiden Formulierungen ergibt für die
technische Arbeit:
4.3-13
Die Differenz ergibt für die technische Arbeit:
Mit der Produktregel der Differentiation lassen sich die ersten beiden Terme auf
der rechten Seite zusammenfassen.
4.3-14
Die technische Arbeit
besitzt demnach zwei Anteile
reversibler Anteil
irreversibler Anteil
Bem.: Der reversible Anteil beinhaltet die kinetischen und potentiellen Energien der Massenströme.
Die gespeicherte potentielle Energie in einem hochgelegen Reservoir wird zum Beispiel als
technische Arbeit bei Wasserkraftanlagen in einer Turbine umgesetzt.
4.3-15
Spezialfall:
1. Hauptsatz für stationären Fließprozess bei reversibler Prozessführung
keine mechanischen Verluste und Wärmezufuhr reversibel
(vergl. die Bemerkungen auf Seite 4.2-13)
4.3-16
Spezialfall:
Adiabater Strömungsprozess (q12 = 0)
ohne technische Arbeit (wt12 = 0),
Bei einem solchen Prozess bleibt die Totalenthalpie konstant.
Das heißt, die Summe der austretenden Totalenthalpieströme ist gleich der Summe
der eintretenden Totalenthalpieströme.
4.3-17
4.4 Die spezifischen Wärmekapazitäten
4.4.1 Änderung der inneren Energie auf Grund von Temperaturänderung
Wegen des 1. Hauptsatz
ist es zweckmäßig isochore Prozesse zu
betrachten, da dann die Volumenänderungsarbeit verschwindet (vgl. 4.7-2):
Bei reversibler Prozessführung ist dann die Änderung der inneren Energie allein
durch die Wärmezufuhr bestimmt:
Wir betrachten
und definieren wegen (*):
spezifische und molare Wärmekapazität bei konstantem Volumen
4.4-1
Bei konstantem Volumen gilt:
Bemerkung:
Wir haben die Änderung der inneren Energie mit der zugeführten Wärme
gekoppelt, indem wir einen isochoren Prozess betrachtet haben:
Für ideale Gase ist die Einschränkung auf einen isochoren Prozess aber nicht
notwendig, da hier wegen
gilt und damit immer:
Der 1. Hauptsatz liefert für ideale Gase:
4.4-2
4.4.2 Änderung der Enthalpie auf Grund von Temperaturänderung
Änderung der Enthalpie auf Grund von Temperaturänderungen bei konstantem
Druck, isobare Prozesse (vgl. 4.7-3):
Wir definieren wegen (*):
spezifische und molare Wärmekapazität bei konstantem Druck
Bei konstantem Druck gilt:
4.4-3
Eine Sonderrolle kommt wieder dem idealen Gas zu:
Wir haben die Änderung der Enthalpie mit der zugeführten Wärme gekoppelt,
indem wir einen isobaren Prozess betrachtet haben:
Für ideale Gase ist die Einschränkung auf einen isobaren Prozess aber nicht
notwendig, da hier wegen
gilt und damit immer:
Der 1. Hauptsatz liefert für ideale Gase:
4.4-4
4.4.3 Spezifische Wärmekapazitäten idealer Gase
Bei idealen Gasen sind die innere Energie und die Enthalpie ausschließlich
Funktionen der Temperatur.
Daher müssen auch die molaren und spezifischen Wärmekapazitäten reine
Temperaturfunktionen sein:
Es gilt ferner:
4.4-5
Ableitung
Ebenso
Verhältnis der spezifischen Wärmen: κ ∗)
Es ergibt sich:
Das Billardkugelmodell des idealen Gases beschreibt im angegebenen Temperaturbereich den Wert für einatomige Gase richtig (vergl. 4.2-19):
Verhältnis der spezifischen Wärmen κ spielt eine besondere Rolle. Wir werden sehen, dass für die
idealen Gase κ gleich dem Isentropenxponenten k ist (vergl. 4.7-6)
*) Das
4.4-6
Das Verhältnis der spezifischen oder der molaren Wärmen
nimmt bei Umgebungstemperatur näherungsweise folgende Zahlenwerte an:
Einatomige Gase:
κ = 5/3 = 1,66
Zweiatomige Gase: κ = 7/5 = 1,4
4.4-7
Für mehratomige Gase zeigen Messungen, dass die spezifischen Wärmekapazitäten
deutlich größer und deutlich temperaturabhängig sind:
Für zweiatomige Gase bei Raumtemperatur liest man im vorstehenden Diagramm
folgenden Wert ab:
Zweiatomige Gase können bei diesen Temperaturen noch als starres Hantelmodell
dargestellt werden. Da die innere Energie als die Summe der Energien der frei
betrachteten Moleküle dargestellt werden kann, kommt bei zweiatomigen Gasen zu
den drei Energieanteilen der Translation des Billardkugelmodell noch die
Rotationsenergie um zwei Achsen hinzu.
Nach dem Gleichverteilungssatz erhält im statistischen Mittel jeder Freiheitsgrad
die gleiche innere Energie. Daher ist:
Noch höhere Temperaturen regen Molekülschwingungen und bisher eingefrorene
Freiheitsgrade an, so dass die Wärmekapazitäten mit der Temperatur weiter ansteigen.
4.4-8
Translatorische und rotatorische Freiheitsgrade
Einatomige Gase (Beispiel Edelgase wie He, Ar etc)
Freiheitsgrade der Translation:
3
Freiheitsgrade der Rotation:
alle eingefroren*)
Zweiatomige Gase (Beispiel Gase wie N2, O2 etc)
Freiheitsgrade der Translation:
3
Freiheitsgrade der Rotation:
2 (einer eingefroren*))
Dreiatomige Gase mit gewinkelter Struktur
(Beispiel Gase wie H2O, SO2 etc)
Freiheitsgrade der Translation:
3
Freiheitsgrade der Rotation:
3
Aus den Messwerten lässt sich deshalb folgern, dass CO2 keine
gewinkelte Struktur wie H2O oder SO2 hat!
*) Die Tatsache, dass einige rotatorische Freiheitsgrade eingefroren sind, ist ein quantenmechanischer Effekt und lässt sich
mit der klassischen Physik nicht erklären. Die Quantisierung des Drehimpulses erfordert bei kleinem Trägheitsmoment eine
ausreichend hohe Temperatur, um die Rotation um die entsprechende Achse anzuregen. Alle klassischen Erklärungen
widersprechen dem Gleichverteilungssatz, nachdem jeder Freiheitsgrad die gleiche Energie aufnimmt.
4.4-9
4.4.2 Spezifische Wärmekapazitäten idealer Flüssigkeiten
Annahme: inkompressibel, d. h. konstantes Volumen: dv = 0
1. Hauptsatz liefert mit pdv = 0:
Die innere Energie für ideale Flüssigkeiten ist also nur
von der Temperatur abhängig.
4.4-10
Folgerung für die Enthalpie idealer Flüssigkeiten und cp
Definition der Enthalpie:
Vollständiges Differential:
Vergleich:
⇒ Wärmekapazitäten cp und cv sind gleich für ideale Flüssigkeiten.
Die Enthalpie für ideale Flüssigkeiten ist also von der Temperatur und
vom Druck abhängig:
4.4-11