Aussage

3. Mathematische Aussagen, Notation
Zusammenfassung
Die Mathematik beschäftigt sich mit gewissen "idealen" Objekten (z.B. Zahlen, geometrischen Figuren, ...), ihren Eigenschaften und den zwischen ihnen bestehenden Beziehungen.
Da sich solche Eigenschaften und Beziehungen verbal (umgangssprachlich) oft nur umständlich in Sätzen beschreiben lassen, bedient
sich die Mathematik (wie auch andere Wissenschaften) einer eigenen Fachsprache samt zugehöriger Notation.
Grundvoraussetzung für ein Verständnis von Mathematik ist es daher, ihre "Sprache verstehen" und ihre "Notation entschlüsseln" zu lernen.
In diesem Kapitel befassen wir uns mit der Sprachweise bzw. Notation, mit der die Mathematiker Eigenschaften von Objekten
bzw. Beziehungen zwischen ihnen beschreiben.
Die Kenntnis dieser Notation wird uns im weiteren Verlauf des Unterrichts viel Schreibarbeit abnehmen.
Dabei lernen wir im Folgenden insbesondere die folgende Symbole und Definitionen kennen:
"
$
$!
fl
fi
Ÿ
a fl b
añb
a›b
:a
,
Allquantor; für alle ...
Existenzquantor; für mindestens ein ...
für genau ein ...
Und Verknüpfung, Konjunktion
Oder Verknüpfung, Disjunktion
Verneinung HNegationL einer Aussage
wenn a, dann b
a genau dann, wenn b
a nur dann, wenn b
gilt a
wobei ...
Als Anwendung dieser Notation werden wir uns mit mathematischen Aussagen und Grundbegriffen der mathematischen
Logik beschäftigen. Es gilt:
Eine Aussage kann entweder wahr oder falsch sein.
Allaussagen behaupten, dass die Aussage aHxL für die ganze Grundmenge G gilt: " x œ G : aHxL
Esistenzaussagen behaupten, dass es mindestens ein Element mit der angegebenen Eigenschaft aHxL gibt: $ x œ G : aHxL
Aussage
Die Eigenschaften von mathematischen Objekten oder Beziehungen zwischen ihnen werden in sogenannten Aussagen (in
Form von Behauptungen) verbal oder formalisiert angegeben.
Eine Aussage ist ein Satz, der (in der zweiwertigen Logik) entweder wahr oder falsch ist. Man sagt auch, die Aussage hat einen der
Wahrheitswerte "wahr" oder "falsch" (oder in Zahlen ausgedrückt "1" oder "0").
2
Beispiel für wahre Aussage:
formalisiert:
p>3
verbal:
p ist grösser als 3
Beispiel für falsche Aussage: "4 ist eine Primzahl".
Jeder Aussage a kann somit ein Wahrheitswert wHaL (wahr oder falsch) zugeordnet werden.
Eine Aussageform ist eine Vorstufe einer Aussage. Sie enthält mindestens eine Variable, für welche Zahlen oder allgemeiner gewisse
Elemente eingesetzt werden können. Wird dies getan entsteht eine Aussage, die nun wahr oder falsch sein kann. Gleichungen und
Ungleichungen sind wichtige Beispiele für Aussageformen.
Beispiel
† die Gleichung 2 x + 1 = 9 ist eine Aussageform;
† wenn man x = 4 in die Gleichung einsetzt entsteht eine wahre Aussage 2 * 4 + 1 = 9
† wenn man x = 3 in die Gleichung einsetzt entsteht eine falsche Aussage 2 * 3 + 1 = 9
Die Menge aller Zahlen einer Grundmenge, die eine Aussageform A zu einer wahren Aussage machen, nennt man die Lösungsmenge
HaL (oder auch Erfüllungsmenge) dieser Aussageform.
Zwei Aussageformen a und b sind genau dann äquivalent, wenn HaL = HbL.
Eine Aussage kann eine Eigenschaft für ein einzelnes, konkretes Objekt (wie oben für p) oder aber auch für mehrere Objekte
gleichzeitig behaupten.
Beispiel: Gerade Zahlen sind durch 2 teilbar.
Die Gesamtheit dieser Objekte (bei mehreren Objekten) nennt man die Grundmenge G der Aussage. Solche Aussagen
formuliert man mittels Variablen (z.B. x) und Quantoren (z.B. Allquantor ", Existenzquantor $) . Dabei unterscheidet man
zwischen Allaussagen und Existenzaussagen.
Allaussagen
Allaussagen behaupten, dass die Aussage für die ganze Grundmenge G gilt. Dies kann prägnant mit dem Allquantor " formuliert
werden: " x œ G : aHxL
Hier ist " der Allquantor, G die Grundmenge und aHxL die Eigenschaft.
† allgemein
formalisiert: " x œ G : aHxL
verbal: "Alle x von G haben die Eigenschaft aHxL", "Jedes x von G hat die Eigenschaft aHxL" oder auch "Für alle x von G
gilt die Eigenschaft aHxL".
† speziell
formalisiert: " x œ : 1 » x
verbal: "Alle ganzen Zahlen sind durch 1 teilbar"
† Eine Allaussage ist als falsch entlarvt, wenn man auch nur ein einziges Gegenbeispiel angeben kann. Man sagt dann, dass
die Allaussage falsifiziert wurde. Nachzuweisen, dass eine Allaussage wahr ist, ist meist viel schwieriger durchzuführen.
3
Existenzaussagen
Esistenzaussagen behaupten, dass es mindestens ein Element aus der Grundmenge G mit der angegebenen Eigenschaft gibt. Dies kann
prägnant mit dem Existenzquantor $ formuliert werden: $ x œ G : aHxL
Hier ist $ der Existenzquantor, G die Grundmenge und aHxL die Eigenschaft.
† allgemein
formalisiert: $ x œ G : aHxL
verbal: "Es gibt (mindestens) ein x von G mit der Eigenschaft aHxL"
† speziell
formalisiert: $ x œ : x2 < 5
verbal: "Es gibt mindestens eine ganze Zahl, deren Quadrat kleiner als 5 ist."
† Eine Existenzaussage ist als wahr bestätigt, wenn man auch nur ein einziges Beispiel angeben kann. Man sagt dann, dass
die Existenzaussage verifiziert wurde. Nachzuweisen, dass eine Existenzaussage falsch ist, ist meist viel schwieriger
durchzuführen.
† Wenn man behaupten will, dass die Aussage für genau ein Element gelten soll, verwendet man (statt des Symbols $) das
Symbol $! und schreibt formal: $ ! x œ G : aHxL und spricht "Es gibt genau ein x aus G mit der Eigenschaft aHxL."
Kombination von Allquantor und Existenzquantor
Allquantoren und Existenzquantoren können auch kombiniert werden.
So heisst zum Beispiel
" x œ : $ y œ : y > x in Worten:
† "Zu jeder natürlichen Zahl x gibt es (mindestens) eine natürliche Zahl y, die grösser als x ist."
† oder einfacher ausgedrückt: "Es gibt keine grösste natürliche Zahl"
Bequeme Schreibweise
Aus Bequemlichkeit werden oftmals die Quantoren weggelassen oder in einer kürzeren Form geschrieben. Gemeint ist dabei
das Gleiche. Man schreibt z.B. für das Kommutativgesetz:
† " a, b œ : a + b = b + a
† a + b = b + a, a, b œ oder
oder
† a+b=b+a
Ebenso ist genaugenommen die Gleichung x + 4 = 5 eine Existenzaussage, da wir behaupten, dass es (mindestens) eine (uns
noch unbekannte) Zahl x gibt, welche diese Gleichung erfüllt: d.h. $ x œ : x + 4 = 5.
Negation von Aussagen
Wie in jeder anderen Wissenschaft bemüht man sich auch in der Mathematik, wahre Aussagen zu machen. Wenn eine Aussage a falsch ist, ist die Negation (Verneinung) der Aussage bzw. die Gegenaussage oder gegenteilige Aussage (symbolisch
Ÿ a, gesprochen "nicht a", "non a") wahr.
Die Negation einer Aussage aHxL kann prägnant mit dem Negationssymbol Ÿ bezeichnet werden: Ÿ aHxL.
Es gibt mehrere Möglichkeiten eine Aussage a formal zu verneinen:
† Durch Voranstellen des Negationssymbols: Ÿ a
† Durch Durchstreichen des Symbols: z.B. –
4
† Durch Verwenden der gegenteiligen Eigenschaft: z.B. < statt ¥
Es gilt:
† Die Negation einer Existenzaussage führt auf eine Allaussage bezüglich der gegenteiligen Eigenschaft Ÿ aHxL: d.h.
Ÿ H$ x œ G : aHxLL = " x œ G : Ÿ aHxL.
† Die Negation einer Allaussage führt zu einer Existenzaussage bezüglich der gegenteiligen Eigenschaft Ÿ aHxL: : d.h.
Ÿ H" x œ G : aHxLL = $ x œ G : Ÿ aHxL.
† Die doppelte Verneinung Ÿ HŸ aL stimmt mit der ursprünglichen Aussage a überein: d.h. Ÿ HŸ aL = a.
Verknüpfung von Aussagen
Wenn für Elemente x einer Grundmenge G mehrere Aussagen aHxL, bHxL, ... möglich sind, lassen sich auch verschiedene
Verknüpfungen dieser Aussagen bilden, d.h. dass beispielsweise zwei (allein für sich bestehende) (Teil)aussagen zu einer
neuen Aussage verknüpft werden.
Beispiel:
G = 8Alice, Bob, Claudia, Daniel<
aHxL : x ist männlich, bHxL : x ist älter als 20 Jahre alt
aHxL fl bHxL : x ist männlich und x ist älter als 20 Jahre alt.
Jede Teilaussage (a, b, ...) kann dabei den Wahrheistwert wahr oder falsch (1 oder 0) haben. Ebenso kann die neue Aussage
den Wahrheitswert wahr oder falsch haben.
Bei zwei Teilaussagen (a, b) gibt es 4 verschiedene Kombinationen von Wahrheitswerten (00, 01, 10, 11). Jede dieser
Kombination kann als Ergebnis die zwei Werte 0 oder 1 haben: es gibt also insgesamt 24 = 16 verschiedene logische Verknüpfungen. Die gebräuchlichsten (die auch eine Anlehnung an den Sprachgebrauch haben) sind: And, Or, Nand, Nor, Xor.
Es kann gezeigt werden, dass mit der Negation (¬, !, Not) sowie den beiden logischen Verknüfungen "Und" (And) und
"Oder" (Or) alle diese Kombinationen abgedeckt werden können.
In den nächsten Abschnitten werden die wichtigsten Verknüpfungen und die dazugehörigen Verknüpfungszeichen (auch
Junktoren genannt) kurz besprochen. Die genaue (mathematische) Definition der besprochenen Verknüpfungen kann dem
Abschnitt "Wahrheitstafeln" entnommen werden.
Und Verknüpfung (Konjunktion, And)
Logische Und Verknüpfung (Konjunktion): a fl b bedeutet "a und b" bzw. "sowohl a als auch b"
Die Aussage a fl b ist genau dann wahr, wenn sowohl a als auch b wahr sind.
Oder Verknüpfung (Disjunktion, Or)
Logische Oder Verknüpfung (Disjunktion): a fi b heisst "a oder b" bzw. "entweder a oder b oder auch beides"
Die Aussage a fi b ist genau dann wahr, wenn entweder a oder b oder auch beide wahr sind.
Wenn - Dann Verknüpfung (fi, Subjunktion)
Die "wenn a, dann b" Aussage verknüpft die beiden Aussagen a und b. Die Argumentation und die Herleitung der Wahrheitstafel ist hier etwas subtiler.
5
Wir können beispielsweise von den folgenden Aussagen ausgehen:
a: Wenn "2 + 2 = 0" gilt, dann gilt "3 ÿ 3 = 9"
(01 führt auf wahre Verknüpfung)
b: Wenn "2 + 2 = 0" gilt, dann gilt "3 ÿ 3 = 0"
(00 führt auf wahre Verknüpfung)
c: Wenn "2 + 2 = 4" gilt, dann gilt "3 ÿ 3 = 9"
(11 führt auf wahre Verknüpfung)
d: Wenn "2 + 2 = 4" gilt, dann gilt "3 ÿ 3 = 0"
(10 führt auf falsche Verknüpfung)
Zu a, b: Man kann nichts dagegen einwenden, wenn jemand aus einer falschen Aussage etwas Wahres oder auch etwas
Falsches folgert. Denn der Fall, in dem man die Voraussetzung antrifft und akzeptiert, tritt nie ein. Wir können daher hier
auch nie eine falsche Folgerung durchführen. Daher müssen wir wahr als Wahrheitswert für die Verknüpfung akzeptieren.
Zu c, d:Aus etwas Wahrem können wir natürlich etwas Wahres folgern. Doch aus etwas Wahrem dürfen wir nichts Falsches
ableiten, das hiesse ja Fehler machen. Man sollte in der Logik aus Wahrheiten nicht Unsinn gewinnen können.
Logische Wenn-Dann Verknüpfung (Subjunktion): a fi b heisst "wenn a gilt, dann gilt auch b" oder "wenn a dann b". Das Symbol fl
wird auch mit Implikationszeichen oder Folgepfeil bezeichnet.
Wenn x die Eigenschaft aHxL besitzt, dann besitzt es automatisch auch die Eigenschaft bHxL. Man sagt in diesem Fall, aHxL ist eine
hinreichende Bedingung für bHxL.
Man kann obige Verknüpfung aHxL fl bHxL auch von rechts lesen: bHxL › aHxL. Sprachlich drückt man dies folgendermassen
aus.
Nur dann, wenn x die Eigenschaft bHxL hat, kann es auch die Eigenschaft aHxL haben. bHxL ist eine notwendige Bedingung für aHxL.
Wir wollen uns im Folgenden jedoch nicht mit der dazugehörigen Wahrheitstafel beschäftigen, sondern uns mehr auf die
Anwendungen konzentrieren.
Wir schauen uns die folgenden zwei Aussagen etwas Genauer an:
aHxL:
x teilt die Zahl 10
bHxL:
x teilt die Zahl 50
aHxL fl bHxL Wenn x die Zahl 10 teilt, dann teilt x auch die Zahl 50.
Genau - Dann - Wenn Verknüpfung (ï, Bijunktion)
Die Verknüpfung a ñ b kann man sich als "Wenn-Dann" Verknüpfung vorstellen, die gleichzeitige in beide Richtungen gilt:
d.h. a fl b und b fl a
Wenn a gilt, dann gilt auch b. Wenn b gilt, dann gilt auch a. Die beiden Aussagen a und b sind also gleichwertig.
Logische Genau Dann - Wenn Verknüpfung (Bijunktion): a ï b heisst "b gilt genau dann, wenn a gilt".
Wenn es sich bei den Aussagen a und b um Eigenschaften handelt, dann sind die beiden Eigenschaften äquivalent.
Die Eigenschaft a ist sowohl eine notwendige als auch eine hinreichende Eigenschaft für die Eigenschaft b.
Beispiel (x œ ): aHxL : x = ÅÅÅÅ23 und bHxL : 3 x = 2. Diese beiden Aussagen sind äquivalent.
6
Weitere Verknüpfungen
Weitere bekannte Verknüpfungen sind:
† Nand (Not And, Verneintes Und, kurz ): hier wird einfach der Output von And (Und) negiert (d.h. aus 0 wird 1 und aus
1 wird 0).
† Nor (Not Or, Verneintes Oder, kurz ): hier wird einfach der Output von Or (Oder) negiert.
† Xor (eXclusive Or, Ausschliessendes Oder, kurz ): im Gegensatz zum Oder gilt hier: " a oder b, aber nicht beide ".
Alle diese Verknüpfungen lassen sich auch allein mit den drei Junktoren ¬, fl und fi ausdrücken.
Beispielsweise gilt:
Nand@a, bD = a NAnd b = a b = Ÿ a fi Ÿ b
Xor@a, bD = a Xor b = a b = Ha fl Ÿ bL fi Hb fl Ÿ aL
Nor@a, bD = a Nor b = a b = Ÿ a fl Ÿ b
Mit den sogenannten Waheitstafeln lassen sich alle diese Verknüpfungen anschaulich darstellen.
NAnd () Gatter
NAnd-Gatter spielen in der Digitaltechnik die Rolle eines Standardbausteins, da sich bereits allein mit ihnen alle logischen
Verknüpfungen und somit auch komplexere Schaltungen (wie Addierer, Multiplexer etc.) zusammenstellen lassen. Es gilt:
Ÿa=a a
a fl b = Ha bL Ha bL
a fi b = Ha aL Hb bL
Dadurch, dass sich mit diesem Baustein alle anderen ersetzen lassen, wird eine Schaltung wesentlich preisgünstiger.
Muss z. B. ein Eingangssignal lediglich negiert werden, so muss kein neuer IC gekauft werden, sondern man legt die Eingangspins (Anschlüsse) so zusammen, dass nur noch ein Eingang zur Verfügung steht. Damit ist ein Nicht-Gatter entstanden. Mit
einer geringeren IC-Anzahl können also Schaltungen umgesetzt werden, da die Hardware-Bausteine komplett ausgenutzt
werden können.
Wahrheitstafeln
Um möglichen Missverständnissen (z.B. bei der Oder Verknüpfung) vorzubeugen, werden in der Logik alle überhaupt
denkbaren logischen Verknüpfungen mittels Wahrheitstafeln (wo die Outputs für die verschiedenen Input Kombinationen
angegeben werden) definiert und mit speziellen Symbolen dargestellt.
In diesen Tabellen bedeutet 0, dass die Aussage falsch ist, und 1, dass die Aussage wahr ist.
Wahrheitstafel für logische Verknüpfungen
7
a
b
Not
¬a
0
1
0
1
0
0
1
1
1
0
1
0
Und Oder Nand aflb afib
¬(aflb)
0
0
0
1
0
1
1
1
1
1
1
0
Nor ¬(afib)
Xor ⇒
1
0
0
0
0
1
1
0
1
0
1
1
1
0
0
1
Bemerkung:
† In obiger Tabelle bedeutet beispielsweise, dass a fl b nur dann 1 (wahr) ist, wenn sowohl a als auch b wahr sind.
† Bei Nor wird einfach der Eintrag von Oder (Or) verneint: d.h. aus 0 wird 1 und aus 1 wird 0.
† Bei zwei Inputs (a und bL gibt es ingesamt i = 22 verschiedene Input Kombinationen und o = 2i = 24 = 16 verschiedene
Outputs.
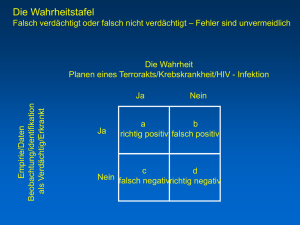
Wenn nur eine Verknüpfung dargestellt werden soll, kann man dies auch mit einer sogenannten Vierfeldertafel machen.
Diese Tafel hat etwas weniger Einträge als die entsprechende Wahrheitstafel.
aflb
0
1
0
1
0
0
0
1
Es lassen sich auch zusammengesetzte Ausdrücke mit mehreren Junktoren bilden (z.B. a fl b fi c). In solchen Fällen sind aus
Eindeutigkeitsgründen Klammerungen sinnvoll. Es gilt ausserdem die folgende Vereinbarung:
¬ bindet stärker als fl
fl bindet stärker als fi
fi bindet stärker als fl
fl bindet stärker als ñ
Weiters wird bei gleichen Junktoren von links geklammert (sog. Linksassoziativität).
8
Aufgaben
3.1 Wahre Aussage
Setzen Sie eines der Zeichen œ , – , = , < bzw. > so dass eine wahre Aussage entsteht:
2
81, 2, 3<
4
81, 2, 3<
p
22
ÅÅÅÅ
ÅÅ
7
ÅÅÅÅ34
0.75
0.3
ÅÅ13ÅÅ
10002
1003
3.2 In Worten
Wie lautet die folgende Aussage in Worten:
a.
$ xœ:
b.
" xœ:$ yœ: y> x
15 < x < 19 fl x œ (wobei die Menge der Primzahlen ist)
Lösung
a. "Es gibt (mindestens) eine ganze Zahl, die grösser als 15, kleiner als 19 und eine Primzahl ist."
b. "Zu jeder natürlichen Zahl x gibt es (mindestens) eine natürliche Zahl y, die grösser als x ist."
oder einfacher ausgedrückt: "Es gibt keine grösste natürliche Zahl"
3.3 Doppelte Verneinung
Drücken Sie den Sachverhalt einfacher (d.h. ohne doppelte Verneinung) aus:
1.
Es gilt nicht: 2 ist nicht Teiler von 25
2.
Ÿ H1 – L
3.
± x œ : x ist nicht Teiler von x
Lösung
1.
Es gilt: 2 ist Teiler von 25
2.
1œ
3.
$ x œ : x» x
3.4 Wahrheitstafel
Überprüfen Sie mit Hilfe einer Wahrheitstafel, ob a fl Hb fi cL = Ha fl bL fi c gilt.
9
Lösung
Wie man der folgenden Wahrheitstafel entnehmen kann, gilt diese Beziehung a fl Hb fi cL = Ha fl bL fi c nicht.
a
1
1
1
1
0
0
0
0
b
1
1
0
0
1
1
0
0
c
1
0
1
0
1
0
1
0
b fi v
LHS
afl(bfic)
a fl b
RHS
Ha fl bL fi c
1
1
1
0
1
1
1
0
1
1
1
0
0
0
0
0
1
1
0
0
0
0
0
0
1
1
1
0
1
0
1
0
3.5 Wahrheitstafel
Überprüfen Sie mit Hilfe einer Wahrheitstafel, ob Ÿ Ha fl bL = Ÿ a fl Ÿ b gilt.
Lösung
Wie man der folgenden Wahrheitstafel entnehmen kann, gilt diese Beziehung (Ÿ Ha fl bL = Ÿ a fl Ÿ b) nicht.
a
0
0
1
1
b
0
1
0
1
a fl b ¬ Ha fl bL ¬a
LHS
0
0
0
1
1
1
1
0
1
1
0
0
¬ b ¬ a fl ¬ b
RHS
1
0
1
0
1
0
0
0
3.6 Wahrheitstafel
Zeigen Sie mit Hilfe einer Wahrheitstafel, dass sich Nand, Nor und Xor auch allein mit den Junktoren ¬, fl und fi in der
folgenden Form ausdrücken lassen.
Nand@a, bD = a b = Ÿ a fi Ÿ b
Xor@a, bD = a b = Ha fl Ÿ bL fi Hb fl Ÿ aL
Nor@a, bD = a b = Ÿ a fl Ÿ b
Lösung
a b = Ÿ a fi Ÿ b
10
a
0
0
1
1
b
a fl b ¬ Ha fl bL ¬a
= ab
0
1
0
1
0
0
0
1
1
1
1
0
¬ b ¬ a fi ¬ b
1
1
0
0
1
0
1
0
1
1
1
0
a b = Ha fl Ÿ bL fi Hb fl Ÿ aL
a
0
0
1
1
b
a b ¬a
0
1
0
1
0
1
1
0
¬ b a fl ¬ b b fl ¬ a RHS
1
1
0
0
1
0
1
0
0
0
1
0
0
1
0
0
0
1
1
0
a b = Ÿ a fl Ÿ b
a
0
0
1
1
b
a fi b ¬ Ha fi bL ¬a
= ab
0
1
0
1
0
1
1
1
1
0
0
0
1
1
0
0
¬ b ¬ a fl ¬ b
1
0
1
0
1
0
0
0
3.7 Existenzquantor
Schreiben Sie die folgenden Aussagen unter Verwendung des Symbols $. Im Falle einer wahren Behauptung ist mindestens
ein Beispiel anzugeben.
a. Es gibt ein x œ : ÅÅÅÅ1x < x
b. Es gibt ein x œ : ÅÅÅÅ1x < 1
1
c. Es gibt ein x œ : ÅÅÅÅ1x < ÅÅÅÅ
ÅÅÅÅÅÅ
x-1
1
d. Es gibt ein x œ : ÅÅÅÅ1x < ÅÅÅÅ
ÅÅÅÅÅÅ
x+1
Lösung
a. $ x œ : ÅÅ1xÅÅ < x
Bsp. ÅÅÅÅ15 < 5
b. $ x œ : ÅÅÅÅ1x < 1
Bsp. ÅÅÅÅ15 < 1
1
c. $ x œ : ÅÅÅÅ1x < ÅÅÅÅ
ÅÅÅÅÅ
x-1
Bsp. ÅÅÅÅ15 < ÅÅÅÅ14
1
d. $ x œ : ÅÅÅÅ1x < ÅÅÅÅ
ÅÅÅÅÅÅ
x+1
Bsp. ÅÅÅÅ-11ÅÅÅÅ < ÅÅÅÅ11ÅÅ fl -2 < 2
ÅÅÅÅ2ÅÅÅ
ÅÅ2ÅÅ
11
3.8 Äquivalenz (ï) und Implikation (fi)
Überprüfen Sie, ob die angegebenen Paare von Bedingungen äquivalent sind oder nicht.
a. G = : x > 2 sowie x2 > 4
b. G = : x > 2 sowie x2 > 4
c. G = : 3 x = 56 sowie 6 x + 5 = 15
d. G = : xHx - 2L = 0 sowie 5 x - 10 = 0
e. G = , n œ : x = 2 n sowie "x ist gerade"
Lösungen
a. Hx > 2L ñ Hx2 > 4L
Dies ist eine sowohl hinreichende als auch notwendige Bedingung.
b. Hx > 2L fl Hx2 > 4L
Dies ist eine hinreichende Bedingung. Sie ist jedoch nicht notwendig: Gegenbeispiel x = -3.
56
c. Die Lösungen sind ÅÅÅÅ
ÅÅ bzw. ÅÅÅÅ53 . Sie sind nicht äquivalent.
3
d. Die Lösungen sind {0, 2} bzw. {2} . Sie sind nicht äquivalent.
e. Die beiden Bedingungen sind äquivalent.
3.9. Präzedenz und Linksassoziativität
Berechnen Sie:
0 fi 1 fl 1
0 fl 1 fl 1
Ÿ 0 fl 1 fi 0
1 fl H0 fl 1L
1 fl Ÿ 0 fl 1
1 fl Ÿ H0 fi 1L
Lösung
Die Lösungen sind:
0 fi 1 fl 1 = 0 fi 1 = 1
0 fl 1 fl 1 = 0 fl 1 = 0
Ÿ 0 fl 1 fi 0 = 1 fl 1 fi 0 = 1 fi 0 = 1
1 fl H0 fl 1L = 1 fl 0 = 0
1 fl Ÿ 0 fl 1 = 1 fl 1 fl 1 = 1
1 fl Ÿ H0 fi 1L = 1 fl Ÿ 1 = 1 fl 0 = 0
12
3.10 NAnd Gatter
Zeigen Sie, dass gilt:
Ÿa=a a
a fl b = Ha bL Ha bL
a fi b = Ha aL Hb bL
Lösung
Ÿa=a a
a
¬a
afla
¬(afla)
0
1
1
0
0
1
1
0
a fl b = Ha bL Ha bL
a
b
0
0
1
1
a fl b a b (ab)(ab)
0
1
0
1
0
0
0
1
1
1
1
0
0
0
0
1
a fi b = Ha aL Hb bL
a
0
0
1
1
b
0
1
0
1
a fi b a a b b Ha aL Hb bL
0
1
1
1
1
1
0
0
1
0
1
0
0
1
1
1
3.11 NAnd Gatter
Warum sind NAnd Gatter in logischen Schaltungen so wichtig?
Lösung
Mit logischen Gattern lassen sich alle anderen logischen Gatter realisieren.
Auf einem IC (Integrated Circuit) müssen deshalb nur NAnd Gatter aufgebracht werden und durch entsprechende Verknüpfung dieser Gatter (wird durch sogenanntes Brennen erreicht) lässt sich dann jede logische Schaltung realisieren.