Grundlagen der Elektrotechnik II

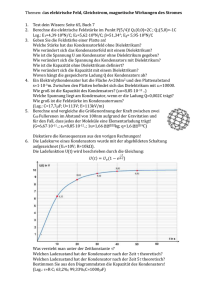
Grundlagen der Elektrotechnik II
Übungsaufgaben
1) Lorentz-Kraft
q = −e = −1.602 · 10−19 As iegt mit der
schwindigkeit ~
v = (vx , vy , vz ) = (0, 35, 50) km/s durch ein
~ = (Bx , By , Bz ) = (0, 0, −20)
gnetfeld mit der Flussdichte B
Ein
a)
Elektron
Berechnen Sie die Kraft, die auf das Elektron wirkt.
GeMamT.
(Lsg.:
112 · 10−18 N)
2) TV-Röhre
In einer Fernsehbildröhre wird der Elektronenstrahl
durch magnetische Ablenkfelder gesteuert. Ein Elektron
wird
in
der
gezeigten
Röhre
durch
das
elek-
trische Feld zwischen Kathode (K) und Anode (A)
auf die Geschwindigkeit
sieren
cke
der
der
Anode
beschleunigt. Nach Pas-
durchläuft
d=5
Dicke
v
cm
ein
es
auf
homogenes
B = 0.6
sches Ablenkfeld der Stärke
einer
Stre-
magneti-
mT, wo es auf
einen Kreisbogen vom Radius R = m · v/q · B gezwun4
−31
gen wird (l = 0.5 m, v = 10 km/s, m = 9.1 · 10
kg,
−19
q = −1.602 · 10
As).
a)
Berechnen Sie die Ablenkung x auf dem Schirm.
(Lsg.:
32.4 cm)
3) Magnetfeldstärke
Ein gerader Leiter der Dicke
Stärke
a)
I = 3.5 A
d = 6 mm
wird von einem Gleichstrom der
durchossen.
Berechnen Sie die magnetische Feldstärke im Abstand
r3 = 20 cm,
von der Leiterachse.
(Lsg.:
r1 = 5 cm, r2 = 10 cm
und
11.14 A/m , 5.57 A/m , 2.78 A/m)
b)
Berechnen Sie die Induktion an diesen Orten. (Lsg.: 14·10−6 V s/m2 , 7·10−6 V s/m2 , 3.5·10−6 V s/m2 )
c)
Berechnen Sie die magnetische Feldstärke auf der Leiteroberäche. (Lsg.: 185.7 A/m)
d)
Stellen Sie
H(r)
auÿerhalb des Leiters grasch dar.
4) Magnetfeld, (gegensinnig)
Zwei parallel verlaufende dünne Drähte (Hin- und Rückleiter) im
Abstand von
a)
cm führen je 25 A.
Berechnen Sie die magnetische Feldstärke zwischen den Leitern in den Punkten
b = 10
b)
x = 35
cm,
c=5
cm und
d = 17.5
cm.
(Lsg.:
45.47 A/m , 55.71 A/m , 92.84 A/m , 22.74 A/m)
Berechnen Sie die magnetische Flussdichte in diesen Punkten.
(Lsg.:
57.1 µT , 70 µT , 116.7 µT , 28.6 µT )
1
a = 17.5
cm,
5) Magnetfeld, (gleichsinnig)
Zwei parallel verlaufende dünne Drähte (Hin- und Rückleiter) im
Abstand von
a)
cm führen je 25 A.
Berechnen Sie die magnetische Feldstärke zwischen den Leitern in den Punkten
b = 10
b)
x = 35
cm,
c=5
cm und
d = 17.5
cm.
(Lsg.:
a = 17.5
0 A/m , 23.87 A/m , 66.32 A/m , 22.74 A/m)
Berechnen Sie die magnetische Flussdichte in diesen Punkten.
(Lsg.:
0 T ,
30 µT , 83.34 µT , 28.6 µT )
6) Magnetfeld, mittig zwischen zwei Leitern
Zwei parallel verlaufende dünne Drähte (Hin- und Rückleiter) im
Abstand
a)
2a
führen je den Strom
I1 = I2 = I .
Geben Sie den Verlauf der magnetische Feldstärke
Funktion von y an.
(Lsg.:
H(a, y) =
H(a, y)
entlang der y-Achse als
a·I
)
π(a2 +y 2 )
7) Biot-Savart, Rechteckleiter
Eine quadratisch geformte Leiterschleife mit der Seitenlänge
wird von einem Gleichstrom
a)
I = 2.5 A
2a = 12 cm
durchossen.
Berechnen Sie die magnetische Feldstärke im Zentrum der Schleife.
(Lsg.:
18.76 A/m)
8) Biot-Savart, Ringleiter
Ein Ringleiter, bestehend aus einem sehr dünnen Draht, wird von einem
Gleichstrom
I
durchossen.
a)
Geben Sie den Verlauf der magnetische Feldstärke
q
I
x 2 3
) · (1 + ( R
) ) )
(Lsg.: H = ( 2R
b)
Stellen Sie den Verlauf der Funktion
H( Rx )
2
H( Rx )
grasch dar.
entlang der x-Achse an.
cm,
9) Kraft, Drei-Leitersystem
Drei parallel verlaufende Leiter sind so angeordnet, dass sie Ecken
a = 20 cm bilden.
I1 = 20 A, I2 = 40 A und
eines gleichseitigen Dreiecks mit der Seitenlänge
In den Leitern ieÿen die Gleichströme
I3 = 60 A.
a)
Berechnen Sie die magnetischen Feldstärken auf den Achsen der einzelnen Leiter.
(Lsg.:
b)
42 A/m, 42 A/m, 42 A/m)
Berechnen Sie pro Meter Leiterlänge die an den Leitern angreifenden Kräfte.
(Lsg.:
1.06 · 10−3 N/m, 2.12 · 10−3 N/m, 3.18 · 10−3 N/m)
10) Kraft, Leiterwinkel
In einem homogenen Magnetfeld mit der Induktion
B = 1.2 T
ben-
det sich ein rechtwinkliges Stück eines Drahtleiters, das vom Strom
I = 1 A durchossen wird. Die Gesamtlänge des Drahtwinkels beträgt
2 · L = 6 cm.
a)
Berechnen Sie den Betrag der Kraft, die an einem Drahtschenkel angreift. (Lsg.: 36·10−3 N)
b)
Berechnen Sie die Gesamtkraft auf den Drahtwinkel. (Lsg.: 51 · 10−3 N)
c)
Welche Richtung hat die Gesamtkraft? (Lsg.: )
11) Drehspul-Messinstrument
I = 1 mA ieÿt durch die rechteckförmige Spu(N = 200 Wdgn, l = 10 mm, b = 10 mm) eines Messinstruments.
Ein Gleichstrom
le
Die
Spule
(BL
=1
a)
bendet
sich
im
Luftspalt
eines
T). Das Federgegenmoment ist
MG =
Permanentmagneten
0.4 · 10−6 Nm/Skt.
Berechnen Sie den Zeigerausschlag des Drehspulmesswerks.
(Lsg.:
50 Skalenteile)
12) Motorstrom
Auf dem Anker (Durchmesser
D = 44
cm) einer Gleichstrommaschi-
ne benden sich 200 stromdurchossene Stäbe (Länge: je 20 cm) im
Luftspalt der Maschine. Die Flussdichte im Luftspalt ist
das Drehmoment beträgt
a)
Md = 150
BL = 0.72
T,
Nm.
Berechnen Sie den Strom, der durch die Ankerwicklung ieÿt.
3
(Lsg.:
23.66 A)
13) Induktion, bewegter Stab
l = 4 cm wird mit der Geschwindig◦
Winkel von α = 60 durch ein homogenes
Ein metallischer Stab der Länge
v = 80 cm/s in einem
Feld (B = 0.5 T ) bewegt.
keit
a)
Berechnen Sie die Spannung an den Stabenden.
(Lsg.:
13.8 mV)
14) Induktion, bewegter Rahmen
= 57 · 106 S/m) mit der
Drahtstärke d = 2 mm bendet
Ein quadratischer Kupferrahmen (γCu
tenlänge
a = 4 cm
und der
Seisich
im homogenen Feld eines Permanentmagneten mit der Induktion
B = 1.6 T .
Der Rahmen wird schlagartig (v
= 5 m/s)
quer zu den
Feldlinien aus dem Feld herausgezogen.
a)
Berechnen Sie den ohm'schen Widerstand des Rahmens.
b)
Berechnen Sie den induzierten Strom im Rahmen und die erforderliche Kraft.
(Lsg.:
(Lsg.:
0.89 mΩ)
359.5 A , 23 N)
15) Induktion, Kurzschlussring
Ein Kurzschlussring (R
= 1.6 mΩ, D = 16 mm)
liegt
voll im Luftspalt eines Elektromagneten. Der Magnet
wird eingeschaltet und baut innerhalb von
die Flussdichte
1.2 T
35 ms linear
auf.
a)
Berechnen Sie den induzierten Strom im Ring.
b)
Der Ring wird zu einer ∞ verdreht (keine Berührung im Kreuzungspunkt der Drähte). Wie groÿ ist der Strom jetzt?
(Lsg.:
0 A)
4
(Lsg.:
4.3 A)
16) Magnetfluss, Koax-Leitung
Gegeben ist eine koaxiale Leitung mit den Abmessungen:
D = 16 mm
d = 7 mm,
Da = 18 mm. Die Leitung
führt einen Gleichstrom I = 3.5 A. Berechnen Sie pro 1 m Leiterlänge
den magnetischen Fluss φ
a)
und dem Auÿendurchmesser
im Raum zwischen Innen- und Auÿenleiter.
(Lsg.:
578.7 nVs)
17) Magnetfluss, Dreieckschleife
Ein gerader, langer Leiter führt den Strom
I = 25 A. Im Abstand
a = 10 cm bendet sich eine Leiterschleife. Sie hat die Form eines
gleichschenkligen Dreiecks mit den Abmessungen h = 16 cm und
g = 20 cm.
a)
Berechnen Sie den magnetischen Fluss durch die Leiterschleife.
18) Zylinderspule, Solenoid
l = 30 cm und der
Stärke 0.8 mm dicht
Eine langgestreckte Zylinderspule der Länge
Dicke
d=5
cm ist mit einem Draht der
an dicht einlagig über ihre volle Länge bewickelt. Innerhalb der
Spule beträgt die Induktion
5
mT.
a)
Berechnen Sie die Induktivität der Spule.
b)
Berechnen Sie den Spulenstrom.
(Lsg.:
(Lsg.:
1.157 mH)
3.18 A)
19) Toroidspule
Auf
einem
l = 200 mm
Kunststoring
ist eine Spule mit
mit
dem
N = 1000
mittleren
Umfang
Windungen (gleichmä-
ÿig, dicht an dicht auf dem Umfang verteilt) aufgebracht. Die von
2
einer Windung eingeschlossene Fläche beträgt A = 175 mm . In
der Spule soll durch Einspeisung eines Stroms
−6
Fluss von φ = 1.5 · 10
W b erzeugt werden.
a)
I
ein magnetischer
Berechnen Sie die erforderliche Stromstärke I.
5
(Lsg.:
1.36 A)
(Lsg.:
4 · 10−7 Vs)
20) Spule auf Ferritkern
Eine Wicklung mit
I = 10
a)
N = 1000
Wdgn erzeugt mit einem Strom von
−4
mA im Ferritkern einen Gesamtuss von φ = 3 · 10
Vs.
Berechnen Sie die Induktivität der Spule.
(Lsg.:
30 H)
21) Spule auf Ringkern
Ein
N = 1000
a)
(lRe
Ringkern
= 10
AF e = 1 cm2 ,
cm,
µr = 5000)
ist
mit
Wdgn bewickelt.
Berechnen Sie die Induktivität der Spule.
(Lsg.:
6.28 H)
22) Induktivität, Koax-Kabel
l = 15 cm und den
ri = 0.4 mm ist an ihrem
Eine luftgefüllte Koax-Leitung mit der Länge
Querabmessungen
ra = 3.25
mm und
Ende kurzgeschlossen.
a)
Berechnen Sie die äuÿere Induktivität
b)
Berechnen Sie die äuÿere Induktivität
Ferritmaterial (µr
(Lsg.:
= 2000)
La der Leitung. (Lsg.:
La , wenn die Leitung
aufgefüllt ist.
62.88 µH )
23) Gegeninduktivität
Ein Übertrager besteht aus 2 Wicklungen mit den Induktivitäten
320
mH und
erhält man
445
800
mH. Bei Reihenschaltung der Wicklungen
mH.
a)
Berechnen Sie die Gegeninduktivität
b)
Berechnen Sie den Koppelfaktor.
M.
(Lsg.:
(Lsg.:
0.667)
6
337.5 mH)
62.85 nH)
über die halbe Länge mit