PHYSIK GRUNDWISSEN 8

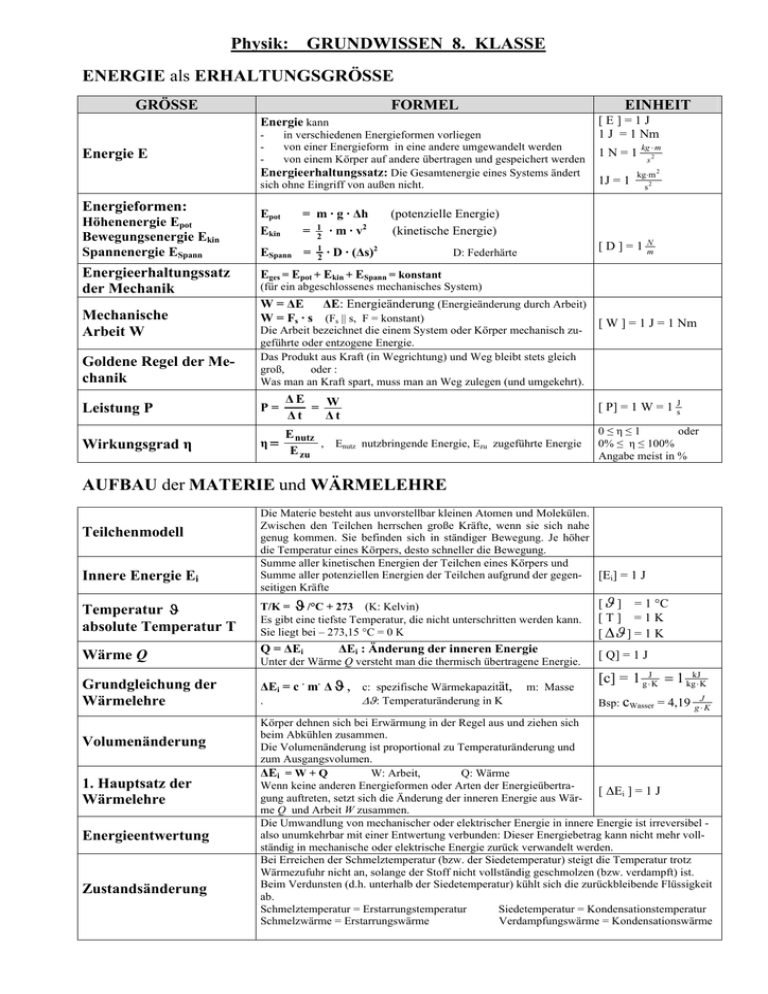
Physik:
GRUNDWISSEN 8. KLASSE
ENERGIE als ERHALTUNGSGRÖSSE
GRÖSSE
FORMEL
EINHEIT
Energie kann
Energie E
Energieformen:
Höhenenergie Epot
Bewegungsenergie Ekin
Spannenergie ESpann
Energieerhaltungssatz
der Mechanik
Mechanische
Arbeit W
-
in verschiedenen Energieformen vorliegen
von einer Energieform in eine andere umgewandelt werden
von einem Körper auf andere übertragen und gespeichert werden
Energieerhaltungssatz: Die Gesamtenergie eines Systems ändert
sich ohne Eingriff von außen nicht.
Epot
Ekin
= m · g · Δh
= 12 · m · v2
ESpann =
1
2
[E]=1J
1 J = 1 Nm
1N=1
1J = 1
kg ⋅ m
s2
kg⋅m 2
s2
(potenzielle Energie)
(kinetische Energie)
· D · (Δs)2
[D]=1
D: Federhärte
N
m
Eges = Epot + Ekin + ESpann = konstant
(für ein abgeschlossenes mechanisches System)
W = ΔE ΔE: Energieänderung (Energieänderung durch Arbeit)
W = Fs · s (Fs || s, F = konstant)
[ W ] = 1 J = 1 Nm
Goldene Regel der Mechanik
Die Arbeit bezeichnet die einem System oder Körper mechanisch zugeführte oder entzogene Energie.
Das Produkt aus Kraft (in Wegrichtung) und Weg bleibt stets gleich
groß,
oder :
Was man an Kraft spart, muss man an Weg zulegen (und umgekehrt).
Leistung P
P=
ΔE
W
=
Δt
Δt
[ P] = 1 W = 1 sJ
Wirkungsgrad η
η=
E nutz
, Enutz nutzbringende Energie, Ezu zugeführte Energie
E zu
0≤η≤1
oder
0% ≤ η ≤ 100%
Angabe meist in %
AUFBAU der MATERIE und WÄRMELEHRE
Teilchenmodell
Innere Energie Ei
Die Materie besteht aus unvorstellbar kleinen Atomen und Molekülen.
Zwischen den Teilchen herrschen große Kräfte, wenn sie sich nahe
genug kommen. Sie befinden sich in ständiger Bewegung. Je höher
die Temperatur eines Körpers, desto schneller die Bewegung.
Summe aller kinetischen Energien der Teilchen eines Körpers und
Summe aller potenziellen Energien der Teilchen aufgrund der gegen- [Ei] = 1 J
seitigen Kräfte
Temperatur ϑ
absolute Temperatur T
T/K = ϑ /°C + 273 (K: Kelvin)
Es gibt eine tiefste Temperatur, die nicht unterschritten werden kann.
Sie liegt bei – 273,15 °C = 0 K
[ ϑ ] = 1 °C
[T] =1K
[ Δϑ ] = 1 K
Wärme Q
Q = ΔEi
[ Q] = 1 J
Grundgleichung der
Wärmelehre
ΔEi = c . m. Δ ϑ , c: spezifische Wärmekapazität,
Volumenänderung
1. Hauptsatz der
Wärmelehre
Energieentwertung
Zustandsänderung
ΔEi : Änderung der inneren Energie
Unter der Wärme Q versteht man die thermisch übertragene Energie.
.
Δϑ: Temperaturänderung in K
m: Masse
[c] = 1 g ⋅JK = 1 kgkJ⋅ K
Bsp: cWasser = 4,19
J
g⋅K
Körper dehnen sich bei Erwärmung in der Regel aus und ziehen sich
beim Abkühlen zusammen.
Die Volumenänderung ist proportional zu Temperaturänderung und
zum Ausgangsvolumen.
ΔEi = W + Q
W: Arbeit,
Q: Wärme
Wenn keine anderen Energieformen oder Arten der Energieübertra[ ΔEi ] = 1 J
gung auftreten, setzt sich die Änderung der inneren Energie aus Wärme Q und Arbeit W zusammen.
Die Umwandlung von mechanischer oder elektrischer Energie in innere Energie ist irreversibel also unumkehrbar mit einer Entwertung verbunden: Dieser Energiebetrag kann nicht mehr vollständig in mechanische oder elektrische Energie zurück verwandelt werden.
Bei Erreichen der Schmelztemperatur (bzw. der Siedetemperatur) steigt die Temperatur trotz
Wärmezufuhr nicht an, solange der Stoff nicht vollständig geschmolzen (bzw. verdampft) ist.
Beim Verdunsten (d.h. unterhalb der Siedetemperatur) kühlt sich die zurückbleibende Flüssigkeit
ab.
Schmelztemperatur = Erstarrungstemperatur
Siedetemperatur = Kondensationstemperatur
Schmelzwärme = Erstarrungswärme
Verdampfungswärme = Kondensationswärme
ELEKTRISCHE ENERGIE
GRÖSSE
Elementarladung e
Elektrische
Stromstärke I
Elektrische
Spannung U
Elektrischer
Widerstand R
Ohmsches Gesetz
FORMEL
EINHEIT
Das Elektron (Proton) ist Träger einer Elementarladung. Jede in der
Natur beobachtbare elektrische Ladung ist ein ganzzahliges Vielfaches der Elementarladung.
I=
N⋅e
ΔQ
=
Δt
Δt
Q: elektrische Ladung
N: Anzahl der Ladungsträger (Elektronen)
U=
e = 1,6 . 10-19 C
[Q] = 1 C = 1 As
(Amperesekunde)
[ I ] = 1 A (Ampere)
Die elektrische Spannung U einer elektrischen
[ U ] = 1 V (Volt)
Energiequelle gibt an, wie viel potentielle Energie
1 V = 1 CJ
pro Ladung Q zur Verfügung steht.
Δ E pot
Q
Jedes elektrische Bauteil setzt dem Stromfluss einen Widerstand R
entgegen.
R = U
I
In der Regel hängt der Widerstand R von der Temperatur des Leiters
und damit indirekt von der Stromstärke I ab.
[R ] = 1 Ω
1V
1Ω =
1A
U~ I
U = konstant
I
Bei konstanter Temperatur ist der Widerstand eines metallischen Leiters konstant.
Elektrische
Leistung Pel
Pel = U . I
[ P ] = 1 W (Watt)
1 W = 1 VA
Elektrische
Energie Eel
Eel = Pel . Δt = U . I . Δt
[E] = 1 J
1 J = 1Ws
1 kWh = 3,6 ⋅ 106 J
Unverzweigter
Stromkreis
V
U1
U2
R1
(Reihenschaltung von
Widerständen)
Verzweigter
Stromkreis
U
U2
U1
(Parallelschaltung von Widerständen)
A
V
I = I1 = I2
R2
U = U1 + U2
I
R = R1 + R2
R2
A
R1
A
U
A
I2
I = I1 + I2
I1
I
U = U1 = U2
1
R
= R11 + R12
Musteraufgaben
1)
Innere Energie
Mit Hilfe von Eiswürfeln der Temperatur 0,00°C sollen 300 g Apfelsaft von 25°C auf 13°C abgekühlt werden.
Berechne die erforderliche Menge Eis, wenn der Apfelsaft die gleiche spezifische Wärmekapazität wie Wasser
besitzt, und 10 g Eis beim Schmelzen die Wärme 3,34 kJ aufnehmen.
Musterlösung:
Gegeben: Saft: m S = 300 g ;
Eis:
Gesucht:
ϑ S = 25°C ;
ϑ E = 0,0°C ; Δϑ E = 13K ;
Δϑ S = 12 K ;
cW = 4,19
J
gK
Schmelzenergie : E Sch = 334
J
⋅ mE
g
mE
J
m E + cW m E Δϑ E
g
Vom Saft abgegebene Energie : E ab = c w m S Δϑ S
J
J
E auf = E ab ⇔ 334 m E + cW m E Δϑ E = c w m S Δϑ S ⇔ m E (334 + cW Δϑ E ) = c w m S Δϑ S ⇔
g
g
J
4,19
⋅ 300 g ⋅ 12 K
c w m S Δϑ S
gK
mE =
⇔ mE =
⇔ m E = 39 g
J
J
J
334 + cW Δϑ E
334 + 4,19
⋅ 13K
g
g
gK
Lösung: Von Eis und Schmelzwasser aufgenommene Energie : E auf = 334
2)
Schaltung von Widerständen, elektrische Leistung
Der Messbereich des Demonstrationsamperemeters aus der Physiksammlung kann auf folgende Weise von seinem empfindlichsten Messbereich von 2 mA auf den Messbereich von 30 mA erweitert werden:
Weil das empfindliche Messwerk mit dem Widerstand RM = 50,0 Ω höchstens mit der Stromstärke von 2,00 mA
belastet werden darf, leitet man den überschüssigen Strom von 28,0 mA am Messwerk vorbei. Dazu benützt man
einen geeignet geschalteten Widerstand RS, der in der Fachsprache „Shunt“ heißt.
a)
Ist der Shunt in Reihe oder parallel zum Messwerk zu schalten? Begründe deine Antwort.
b)
Welche Spannung fällt am Messwerk des Amperemeters bei Vollausschlag ab?
c)
Berechne den Widerstand des Shunts für die Messbereichserweiterung von 2 mA auf 30 mA.
d)
Berechne den Innenwiderstand des Amperemeters mit dem Messbereich 30 mA unter Berücksichtigung des zugeschalteten Shunts.
e)
Für welche elektrische Leistung muss der Shunt geeignet sein? Was würde passieren, wenn ein Widerstand verwendet würde, der für die maximale Leistung von 1 mW ausgelegt ist?
f) Schaltet man einen Shunt mit dem Widerstand von 4,95 kΩ zwischen Eingangsbuchse und Messwerk, dann
schlägt der Zeiger des Instruments erst bei Anlegen einer relativ hohen Spannung voll aus. Berechne diese
Spannung. In dieser Bauform ist das Instrument ein Voltmeter. Welches ist sein Messbereich?
Musterlösung:
a) Der Shunt ist parallel zum Messwerk zu schalten, da der Strom der Stärke 28mA um das Messwerk herumgeleitet
werden muss.
b) Gegeben:
Maximal erlaubter Strom durch das Messwerk : I M = 2,00 mA
RM = 50,0 Ω
Gesucht: U
Lösung: U
= RM I M ⇔ U = 50,0 Ω ⋅ 2,00 mA ⇔ U = 100 m V
c) Gegeben: Am Messwerk durch den Shunt vorbei geleiteter Strom : I S = 28,0 mA
Spannungsa bfall am Shunt ebenso groß wie am Messwerk ( Parallelsc haltung ) : U = 100 mV
Gesucht: RS
Lösung: RS =
100 mV
U
⇔ RS =
⇔ RS = 3,57 Ω
IS
28,0 mA
⎛ 1
1
1
1
1 ⎞
⎟⎟
d) Lösung:
=
+
⇔ R = ⎜⎜
+
R RM RS
⎝ 50,0 Ω 3,57Ω ⎠
−1
⇔ R = 3,33 Ω
e) Lösung: P = UI S ⇔ P = 0,100 V ⋅ 0,028 A ⇔ P = 2,8 mW
Die elektrische Leistung im Shunt würde die maximal zulässige Leistung von 1,0 mW übersteigen. Der Shunt
würde sich übermäßig erhitzen und möglicherweise durchbrennen.
f) Gegeben: Shuntwiders tan d :
RS ´ = 4950 Ω
Lösung: Gesamtwide rs tan d der Re ihenschalt ung aus Shunt und Messwerk :
R ges = RS ´+ RM ⇔ Rges = 5000 Ω
U = R ges I M ⇔ U = 5000V ⋅ 0,0020 A
⇔ U = 10,0V
3) Energieumwandlungen
Ein Spielzeugfrosch (m = 20 g) wird mit einem Saugnapf unter Spannen einer Feder an einer Tischkante befestigt.
Nach kurzer Zeit springt er in die Höhe, weil der Saugnapf nicht mehr hält. Seine Flugbahn ist etwas seitlich, so dass
er beim Herabfallen die Tischkante verfehlt und bis zum Boden fällt. Die Feder ( D = 5,0
N
cm
) wird vor dem Start um
3,0 cm eingedrückt.
a) Beschreibe allgemein die auftretenden Energieumwandlungen.
b) Berechne die Spannenergie.
c) Welche Geschwindigkeit hat der Frosch zu Beginn des Abhebens?
d) Welche Höhe über dem Tisch erreicht der Frosch?
e) Die Tischkante ist 0,85 m über dem Fußboden. Mit welcher Geschwindigkeit kommt der Frosch am Fußboden an?
Musterlösung:
a) Die anfangs vorhandene Spannenergie der Feder wird beim Entspannen vollständig in die kinetische Energie des
Frosches verwandelt. Diese wandelt sich in Höhenenergie um, welche am höchsten Punkt maximal ist. Die Höhenenergie wird beim Fallen allmählich in kinetische Energie umgewandelt.
b) Gegeben: Δs = 3,0 cm = 0,030 m;
D = 5,0
N
cm
= 500
N
m
;
Gesucht: ESpann
Lösung: ESpann =
1
1
· D · (Δs)2 = · 500
2
2
N
m
· (0,030m)2 = 0,23 J
c) Gegeben: m = 20 g = 0,020 kg;
Gesucht: v
Lösung: ESpann = Ekin
ESpann =
v2 =
1
· m · v2
2
2 ⋅ E Spann
m
d) Gegeben: ESpann;
=
2⋅ 0,23 J
= 4,8
0,020 kg
m = 20 g = 0,020 kg;
m
s
g = 9,8
N
kg
Gesucht: h
Lösung: ESpann = Epot
ESpann = m · g · h
h=
E Spann
m⋅g
=
0,23 J
= 1,2 m
0,020 kg ⋅ 9,8 kgN
e) Gegeben: hT = 0,85 m;
h = 1,2 m;
m = 20 g = 0,020 kg;
Gesucht: vEnde
Lösung: Epot = Ekin
m·g·h=
v=
1
· m · v2
2
2 ⋅ g ⋅ (h + hT ) =
2 ⋅ 9,8 kgN ⋅ 2,05 m = 6,3
m
s
g = 9,8
N
kg