Rudolf-Koch-Schule Physik 12 Gk 1.) Die Dichte der Feldlinien pro

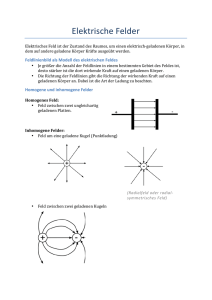
Rudolf-Koch-Schule
Physik 12 Gk
Lösungen: Übung für die Arbeit
1.) Die Dichte der Feldlinien pro
Quadratzentimeter (E) ist ein Maß für die
elektrische Feldstärke. Wir gehen davon
aus, dass die Feldlinien in gleichmäßigen
Abständen radial aus der Mantelfläche des
geladenen Zylinders austreten (Abb.) Der
Zylinder habe die Höhe h und es sollen N
Feldlinien aus dem geladenen Zylinder
austreten. Wir legen um den geladenen
Zylinder einen gedachten Zylinder mit
Radius r und der gleichen Höhe h
(gestrichelt). Seine Mantelfläche A ist
durch das Produkt der Länge der Berandungslinie l und der Zylinderhöhe h gegeben:
A  l h
l  2r

A  2r  h
Im Abstand r von der Mitte des Zylinders ist daher die Dichte der austretenden
Feldlinien E(r) damit durch
N
N 1


E(r)=
2r  h 2h r
gegeben. Da E(r) ein Maß für die elektrische Feldstärke ist, fällt die Feldstärke
1
ebenfalls mit
nach außen ab.
r
2.) Die graue geladene Kugel hat ein radiales
elektrisches Feld. Die gestrichelte Linie
stellt eine Äquipotentiallinie dar. Der dicke
schwarze Punkt ist ein geladener Körper,
der am Anfang und am Ende der Bewegung
entlang der durchgezogenen Linie in
Richtung der Pfeile auf der gestrichelten
Äquipotentiallinie liegt. Da sich die Ladung
des Körpers unterwegs nicht verändert und
die potentielle Energie des Körpers am
Anfang und am Ende der Bewegung gleich
seiner Ladung multipliziert mit dem
elektrischen Potential auf der
Äquipotentiallinie ist, ist diese potentielle Energie insbesondere am Anfang und am
Ende der Bewegung gleich. Hätte der Körper unterwegs Energie verloren oder
hinzugewonnen, dürfte der Energiezustand des Körpers am Ende der Bewegung nicht
genauso sein, wie am Anfang. Es wird lediglich die potentielle Energie des Körpers
unterwegs zum Teil in kinetische Energie umgewandelt, die am Ende der Bewegung
wieder vollständig in potentielle Energie übergeht.
hen, 07.04.2017
phy12-07.doc
Rudolf-Koch-Schule
Physik 12 Gk

3.) Wenn an einem Ort x ein Elektrisches Feld besteht, heißt das, dass, sobald man einen
geladenen Körper an diesen Ort bringt, dieser eine Kraft erfährt. Diese Kraft ist umso

größer, je größer die Feldstärke E dem Betrage nach ist. Die Kraft muss in irgendeine
Richtung wirken. Man schreibt dem Elektrischen Feld die Richtung zu, in der ein
positiv geladener Körper eine Kraftwirkung erfahren würde. Das Feld hat also
Richtung und Betrag. Größen mit diesen beiden Eigenschaften werden durch Vektoren
beschrieben.
d  2  10 15 m
4.) Kernfusion:
a) F 
Q2
. Einsetzen von
40 d 2
1
Q  1,6  10 19 C , d  2  10 15 m und
 0  8,8  10
12
C2
liefert
N m2
F  57,87 N .
b) W  F  d  1,2  10 13 J (Um in einem Protonenplasma den Protonen diese
Energie zu geben, muss man das Plasma auf etwa 10 9 C aufheizen (eine
Milliarde Grad Celsius!!!)
5.) Ein Elektron im Wasserstoffatom:
mv2
1 Q2
a)

r
40 r 2

Länge 2r , dann ist v 
2r

T
v
2r
, wenn T die Umlaufzeit ist. Einsetzen ergibt
T
Q2
bzw. T 
40 m  r
1
Q2
. Ein voller Umlauf hat die
40 m  r
1
2r
Q2
40 m  r
. Einsetzen ergibt:
1
T  3,92  10 16 sec .
1sec
 2,55  1015 Umläufe pro Sekunde.
b) Es schafft
T
2r
m
v
 1,6  10 6
c) v 
und  0,005 , v beträgt also etwa 5 Promille der
T
sec
c
Lichtgeschwindigkeit.
6.) F 
Q2
40 d 2
1
hen, 07.04.2017

Q  F  40  d 2  2,6  10 7 C .
phy12-07.doc