Parametrische Schwingungserregung Haben Sie sich eigentlich

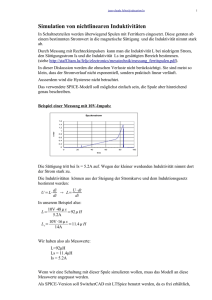
Parametrische Schwingungserregung
Haben Sie sich eigentlich schon einmal gefragt, wie es möglich ist, eine Schaukel auf der man,
sitzt in Schwingung zu versetzen ? Dabei gibt es ja keine Wechselwirkung mit der Umgebung,
wenn man den Luftwiderstand einmal vernachlässigt.
Das ist ein Fall, wie er nicht mit den Newton'schen Gesetzen erklärt werden kann. Denn laut
diesen, muss jede Kraft eine gleich große Gegenkraft besitzen. Das ist aber im Fall der Schaukel
nicht möglich, da keine mechanische Verbindung besteht, über welche die Gegenkraft wirken
könnte. Der Aufhängepunkt nimmt ja nur die Gewichtskraft auf. Alle internen Kräfte, die auf der
Schaukel entstehen müssten sich gegenseitig aufheben, so dass sie sich nie bewegen könnte.
Dass es aber wirklich funktioniert, wird sicher jeder aus seinen Kindheitserfahrungen bestätigen
können.
Nun haben sie die Erklärung für dieses Phänomen schon gefunden ?
Theoretischer Hintergrund
Der Fachausdruck für dieses Phänomen lautet, wie auch der Titel dieser Seite, parametrische
Schwingungserregung. Wie der Name schon sagt, geht es dabei um die Parameter eines
Schwingkreises, welche ja die Schwingungsfrequenz festlegen. Es ist nämlich möglich, durch
periodische Änderungen eines Parameters den Schwingkreis anzuregen. Die Änderungen müssen
natürlich im Takt der Schwingung (welche durch die Resonanzfrequenz vorgegeben ist)
erfolgen, so dass sie sich weiter aufschaukelt.
Das gilt natürlich auch für ein Pendel, welches ja ein mechanischer Schwinger ist. Die
Parameter, die die Schwingfrequenz bestimmen, sind bei einem idealen Pendel nur die Länge des
Pendels (Lage des Massepunktes) und die Schwerkraft. Da eine Schaukel mit einem Pendel
vergleichbar ist, ist es möglich durch richtige Veränderung des Schwerpunktes die Schaukel in
Schwingung zu versetzen. Obgleich auch eine Erregung des Pendels durch
Gravitationsänderung, wie z.B. mit der Gravitationsabschirmung durch Supraleiter, sehr
interessant wäre, aber nicht so einfach zu realisieren ist. Dabei ist dann vielleicht die zur
Änderung der Gravitation nötige Kraft geringer, als der Energiegewinn im Pendel. Dabei ist
dann vielleicht die zur Änderung der Gravitation nötige Kraft geringer, als der Energiegewinn im
Pendel. Wenn man dazu den Supraleiter nur unter dem Pendel hin- und herschiebt, sehe ich
keine Rückwirkung und wenn, dann nur in der vertikalen Richtung wo keine Leistung umgesetzt
werden kann. Bei der klassischen Erregung über Schwerpunktverlagerung ist es, wenn man
selbst auf der Schaukel sitzt, relativ leicht die richtige Gewichtsverlagerung zu finden, um die
Schwingung anzuregen. Das kann jedes Kind auch ohne diese theoretischen Erklärungen.
Um die Schaukel in Schwingung zu versetzen, muss man ihr Energie
zuführen. Energie ist bekanntlich Kraft mal Weg. Als Weg hat man nur die Verschiebung des
Körperschwerpunktes zur Verfügung, doch die Kraft kann sich mechanisch nirgends abstützen.
Nur die Fliehkraft stellt die nötige Gegenkraft zur Verfügung, damit Energie umgesetzt werden
kann.
Ist die Schaukel am Todpunkt, so beginnt man sich zurückzulehnen, was den Schwerpunkt nach
unten verlagert. Erreicht die Schaukel ihren Maximalausschlag, steht man wieder auf und hält
dann den Schwerpunkt hoch, bis sie wieder den Todpunkt erreicht. Dann beginnt das gleiche
Spiel in rückwärtiger Richtung. Nur sehr geübte Schaukler schaffen es, auch den hinteren
Arbeitsgang auszuführen. Der bewegliche Massepunkt auf der Schaukel beschreibt bei richtiger
Masseverlagerung eine liegende Acht. Daraus lässt sich ein wichtiges Merkmal jeder
parametrischen Schwingung erkennen, nämlich die unterschiedlichen Frequenzen des Erregers
und des Schwingkreises. Die Schaukel muss für eine vollständige Periode, ausgehend von einem
Punkt maximaler Auslenkung, einmal hin und auch wieder zurückschwingen. In dieser Zeit führt
der bewegliche Massepunkt aber zwei volle Perioden, von seiner Mittellage aus gesehen, aus.
Im Nulldurchgang ist die Fliehkraft am größten (größte Geschwindigkeit), so dass man von
selbst nach unten gezogen wird. Im Endpunkt ist sie am geringsten und man kann fast verlustfrei
aufstehen. Nur aus der Phasenverschiebung des Tiefpunktes der Masse zum Todpunkt der
Schaukel wird Energie umgesetzt. Wenn die Schaukel verlustfrei schwingt, pendelt die Energie
nur noch zwischen Massepunkt und Schaukel hin und her. Das kann man sich dann so vorstellen,
dass der Massepunkt an einer Feder befestigt ist und nur durch die Fliehkraft bewegt wird. Die
dann entstehende Bahn des Massepunktes ist nur noch eine, der Fliehkraft entsprechende, uförmige Bahn mit der gleichen Frequenz wie die Schaukel. Die beiden Linien, der Acht schieben
sich dann zu einer zusammen. Erst wenn Energie zum Antrieb der Schaukel zugeführt wird, ist
wieder die doppelte Frequenz notwendig. Sie stellt sozusagen die Asymmetrie dar, durch die
Energie ausgekoppelt werden kann.
Das gleiche Prinzip ist auch in der Elektrotechnik anwendbar, wenn die
Induktivität oder die Kapazität eines Schwingkreises verändert wird. Dazu habe ich das
abgebildete Modell gebaut. Es besteht aus einer sehr kuriosen Zusammenschaltung von zwei
Ferrittrafos. Sie sind primär so gepolt, dass sich sekundär ihre Spannungen einander aufheben.
All diejenigen, die dieses Modell sahen, (und die Prinzipien der Spannungsinduktion verstanden)
versicherten mir, dass es nicht funktionieren könnte.
Dennoch wird der Lastwiderstand schon nach kurzer Betriebszeit sehr heiß, und zeigt uns somit,
dass doch Leistung übertragen werden kann. (Es ist fast nichts unmöglich)
Auf den ersten Blick kann diese Schaltung schon nach einem Trick
aussehen. Die Spannung Uq teilt sich gleichmäßig in U1 und U2 auf die beiden Trafos Tr1 und
Tr2 auf. Trafos übersetzen immer mit 180° Phasendrehung, wodurch U1' und U2' gegenpolig
erscheinen. Durch den gegenphasigen Anschluss des Trafos Tr2 tritt aber U2' so auf, dass sie
sich mit U1' zu Null addiert. Am Ausgang dürfte also nie die Spannung UL auftreten. Aber wenn
man erkennt, dass der Lastkreis eigentlich ein Schwingkreis ist, kommt man vielleicht auch
hinter die Funktionsweise. Das Problem ist nur, dass die parametrische Schwingungserregung
relativ unbekannt ist, und deshalb hatte eigentlich jeder dem ich das zeigte so seine Probleme
damit. Warum hört man so etwas nicht in der HTL ! (Vorwurf an die Elektrotechnik- und
Physiklehrer)
Für all diejenigen, die das noch immer nicht glauben können, ist hier der
Beweis mit der Halogenlampe. Wird sie anstelle des Widerstandes eingeschaltet, so leuchtet sie
beim Einsetzen der Schwingung sofort auf. Es ist schon verblüffend, zu sehen, wie zwei Trafos
Leistung übertragen, obwohl sich ihre Ausgangsspannungen eigentlich aufheben sollten !
Wird die Lampe allerdings ohne Kondensator parallel zu den beiden
Trafowicklungen geschaltet, dann tritt das ein, was eigentlich jeder auch schon vorher erwartet
hätte. Es tut sich nämlich gar nichts mehr. Die Trafos pfeifen zwar mit der Oszillatorfrequenz
vor sich hin, da sich ihre Spannungen aber aufheben, gibt es keinen Strom durch die Lampe, und
sie bleibt finster.
Funktion
Die Ferrittrafos werden primärseitig durch kurze Stromimpulse erregt. Diese sind so hoch, dass
das Material dabei in die magnetische Sättigung gelangt. Das hat zu Folge, dass die Induktivität
der Spulen abnimmt. Das ist auch aus folgender Formel ersichtlich:
Ein gesättigter Kern kann keine weiteren Feldlinien mehr aufnehmen, da bereits alle
Elementarmagnete ausgerichtet sind. Siehe zum Verhalten des Eisens im Magnetfeld auch
Barkhausensprünge. Da µ gleich B/H ist, und B in der Sättigung mit Erhöhung von H nicht mehr
ansteigen kann, wirkt sich die Sättigung direkt auf µ aus. Dadurch sinkt auch die Induktivität mit
steigendem Strom ab.
In den Sekundärspulen hebt sich zwar die induzierte Spannung auf, die Induktivität beider
Spulen addiert sich aber wegen der Serienschaltung und der magnetischen Trennung beider
Spulen. Die beiden Sekundärspulen stellen somit eine veränderliche Induktivität dar, welche
durch einen Strom in den Primärspulen verkleinert werden kann. Das ganze funktioniert
natürlich auch in der umgekehrten Richtung. Dann sind nur die Polaritäten an den beiden Spulen
anders.
Das folgende Diagramm zeigt die Kennlinie der Induktivität in Abhängigkeit vom Erregerstrom.
Die Induktivität wurde mit einer Messbrücke bei 1kHz gemessen. Die erregende Gleichspannung
selbst hat auf die Messung keinen Einfluss. Das zeigt schon allein die Tatsache, dass man die
Primärspulen kurzschließen kann, ohne dabei die Anzeige zu ändern. Die induzierten
Spannungen heben sich eben vollständig auf, so dass es keine Spannung gibt, die
kurzgeschlossen werden könnte. Die erregende Gleichspannung selbst kann wegen der
galvanischen Trennung der Trafos auch nicht in die Messbrücke gelangen.
Über diese einstellbare Induktivität kann jetzt ein Schwingkreis nach dem parametrischen
Prinzip erregt werden. Dazu ist keine Spannung am Schwingkreis notwendig. Diese entsteht erst
durch die Schwingung selbst, was mit der Schaukel verglichen werden kann, die ja auch
niemand von außen anstoßen muss. Theoretisch müsste ein kleiner Strom in der Induktivität
fließen, wenn sie sich ändert, denn sonst kann an ihr keine Spannung nach der Formel
auftreten. Da aber immer kleine Spannungen wegen der geringen Unterschiede der beiden Trafos
induziert werden, erregt sich der Schwingkreis in der Praxis immer von selbst.
Aus der obigen Formel ist auch der Term ersichtlich, der für die parametrische Erregung
verantwortliche ist. dL/dt ist in diesem Fall nämlich nicht konstant, und kann ebenfalls eine
Spannung "induzieren". In der Elektrotechnik wird üblicherweise L als Konstante angenommen,
so dass dieser Term wegfällt. Eine Vereinfachung, die nicht immer zutreffend ist, wie man sieht.
Schaltungsbeschreibung
Das Wichtigste an dieser Schaltung ist der Rechteckgenerator,
der die Steuerimpulse für den Schalttransistor erzeugt. Sein Tastverhältnis muss verstellbar sein,
ohne die Frequenz zu beeinflussen. Deshalb wurde hier ein etwas hochwertigerer Generator
(kein NE555, würde damit aber auch funktionieren) verwendet. Er besteht aus einem OPV
TL081, der als Schmitt-Trigger geschaltet ist. Ein Kondensator wird abhängig vom
Ausgangszustand entweder geladen oder entladen, wodurch eine Rechteckschwingung entsteht.
Durch ändern der Verstärkung wird die Kippspannung eingestellt, und somit die Frequenz des
Rechtecksignals. Über einen Rückkoppelwiderstand, der durch zwei Dioden aufgeteilt wird,
kann die Zeit für den Lade- bzw. Entladevorgang getrennt eingestellt werden. Wird dazu wie
hier nur ein Potentiometer verwendet, dann ändert sich die Frequenz mit dem Tastverhältnis
nicht.
Der Nachteil von OPV-Schaltungen ist natürlich die doppelte Versorgung, die sie benötigen. Das
wurde hier mit einem zweiten OPV gelöst, der die 24V in die Hälfte teilt, und somit die
künstliche Masse zu Verfügung stellt.
Der Ausgang des Rechteckgenerators treibt dann den MOSFET-Schalttransistor BUK 453.
Dieser benötigt unbedingt eine Beschaltung gegen Überspannungen, da sich im ausgeschalteten
Zustand kein Freilaufkreis bilden kann, der die Energie aus der Induktivität in den Glättungselko
oder in die Last zurückfließen lässt. Auf der Sekundärseite gibt es ja überhaupt keine induzierte
Spannung !
Das wurde hier mit einem 220Ohm Widerstand R11 und einem 15nF Kondensator C6 gelöst. In
einem gewissen Bereich funktioniert das auch sehr gut. Eine bessere Lösung wäre aber eine
Brückenschaltung, welche die Spannung an der Induktivität zur "Entladung" umpolen kann.
Messungen
An dieser Schaltung wurde eine Reihe von Messungen mit einem Speicheroszilloskop
durchgeführt.
Als erstes gibt es eine Reihe von Bildern, die zeigen, wie die Kerne mit steigendem
Tastverhältnis in Sättigung kommen. Dazu wurde der Primärstrom der Trafos, und die
Steuerimpulse des Transistors oszillografiert. Je größer das Tastverhältnis wird, desto höher ist
auch der erreichte Spitzenwert des Stromes. Ab etwa 30mA Spitzenwert, ist dann eine
überproportionale Zunahme des Stromes zu sehen. Bei 200mA ist die Abweichung von der
idealen Dreieckform bereits so groß, dass nur noch kurze Stromspitzen zu erkennen sind.




Bild 1: Tastverhältnis 25,6%, Spitzenstrom 12mA, keine Sättigungserscheinung
Bild 2: Tastverhältnis 40,0%, Spitzenstrom 25mA, keine Sättigungserscheinung
Bild 3: Tastverhältnis 55,0%, Spitzenstrom 70mA, einsetzen des überproportionalen
Stromanstieges
Bild 4: Tastverhältnis 58,8%, Spitzenstrom 200mA, nadelförmiger Stromverlauf
Wird der Strom (durch das Tastverhältnis) noch weiter erhöht, dann setzt die parametrische
Schwingung schlagartig ein. Nach Einsetzen der Schwingung kann man das Tastverhältnis sogar
wieder etwas zurücknehmen, ohne dass die Schwingung abreißt.
Dann sieht der Strom ganz anders aus, als man erwarten würde.

Bild 5: Tastverhältnis 53,2%, Spitzenstrom 1,2A, sinusförmiger Schwingkreisstrom
Der sinusförmige Primärstrom kommt natürlich aus dem Lastschwingkreis, und wird ebenfalls
parametrisch zurückübertragen. Das nächste Bild zeigt das sehr schön.
Auffällig und charakteristisch für eine parametrische Schwingung ist die
halbe Frequenz des Schwingkreisstromes (in CH1) gegenüber dem erregenden Strom (in CH2).
Der Grund, dafür ist, dass die Induktivität in einer Periode der Lastschwingung zweimal
verändert werden muss (vergl. mit Schaukel), was der doppelten Frequenz für den Primärstrom
entspricht. Das ist eine sehr unübliche Betriebsart eines Transformators. Denn in allen
Betrachtungen wird ja immer von ein und derselben Frequenz auf der Primär- und Sekundärseite
ausgegangen. Man sieht aber, dass er auch so funktionieren kann, und sogar auf sehr seltsame
Weise Leistung übertragen kann. Für alle, die meinen, die doppelte Frequenz kommt nur daher,
da die Trafos mit Gleichstromimpulsen erregt werden, zeigt das nächste Bild die Spannungen an
den Sekundär- und Primärwicklungen.
Zu beachten ist, dass an einer Drossel nie ein Gleichspannungsanteil abfallen
kann (außer ohmschen Verlusten). Die Nulllinie für CH2 liegt deshalb genau im arithmetischen
Mittel der Primärspannung, die somit eine reine Wechselspannung ist. Der Grund für die
einseitige Aussteuerung des Primärstromes liegt in der Freilaufschaltung mit dem RC-Glied.
Dadurch kann sich die Stromrichtung nie Umkehren, sondern es wird fast die gesamte
gespeicherte Energie aus der Drossel am Widerstand umgesetzt. Ein kleiner Teil kann jedoch
auch wieder zurück in den Glättungskondensator fließen. Bei kleinen Strömen funktioniert das
besser, so dass dann auch der Strom ein Wechselstrom ist. (siehe Bild 1,2,3)
Als nächstes wurde versucht mit dem Oszilloskop die Leistung auf der Lastseite zu messen.
Dazu wird der Verlauf von Spannung und Strom (Der Strom wird hier als Spannung am
Lastwiderstand gemessen) miteinander multipliziert, so dass sich die zeitabhängige Leistung
P(t) ergibt. Wird von dieser noch der arithmetische Mittelwert berechnet, so erhält man die
Effektivleistung. Diese Messmethode lässt sich auf der Sekundärseite sehr leicht überprüfen, da
hier ja ein konstanter Widerstand die Leistung umsetzt.

Bild 8: Zeigt die Leistungsmessung auf der Sekundärseite (abgegebene Leistung)
Die folgenden Formeln zeigen, wie die Leistung auf herkömmlicher Weise berechnet werden
kann. Es wurde ja für CH2 der Effektivwert mit 8,84V gemessen. Daraus ergibt sich die
Leistung:
Der errechnete U²-Wert muss nur noch mit dem Shuntwiderstand, der hier gleichzeitig der
Lastwiderstand ist umgerechnet werden. Damit ergibt sich mit dieser Messmethode folgende
Leistung:
Wir sehen also, dass diese Messmethode auch relativ gute Ergebnisse bringt. Deshalb wurde sie
auch auf der Primärseite angewandt. Dort ist eine Spannungsmessung wegen des nicht
konstanten Widerstandes der Trafos nicht mehr möglich. Ein Wattmeter würde bei diesen
Frequenzen auch schon falsche Werte liefern. So bleibt eigentlich nur mehr diese Methode übrig.
Das Bild zeigt wieder die Primärspannung und den dazugehörigen Strom. Dieser wurde jetzt als
Spannungsabfall an einem 1 Ohm Widerstand gemessen. Dabei ergibt sich nur das Problem, dass
man das Oszi in der Mitte Erden muss, und so die Spannung die falsche Richtung erhält. Da bei
eingeschalteter Rechenfunktion leider kein invertieren der Kanäle möglich ist, ergibt sich ein
negativer Wert für den Mittelwert der zeitabhängigen Leistung.

Bild 9: Zeigt die Leistungsmessung auf der Primärseite (aufgenommene Leistung)
Daraus kann man wieder die Leistung wie schon oben nach der Formel
errechnen. Aus diesen beiden Leistungen lässt sich schließlich auch noch der Wirkungsgrad noch
folgender Formel errechnen:
Wenn man die Tatsache berücksichtigt, dass sich die induzierten Spannungen eigentlich
aufheben sollten (!!) ist das ein ganz beachtlicher Wirkungsgrad. Er kommt fast an den Wert bei
Normalbetrieb eines Ferrittrafos heran. Dieser liegt bei weit höheren Frequenzen etwa bei 90%.
Für diese niedrige Frequenz ist also 72% durchaus ein Wert, der auch im Normalbetrieb
entstehen würde.
Messung mit sinusförmiger Spannung
Die bisherigen Betrachtungen beschränkten sich alle auf eine
rechteckförmige Primärspannung. Um zu zeigen, dass dieser ungewöhnliche Betriebsfall eines
Trafos auch bei sinusförmiger Spannung möglich ist, wurde der Aufbau über einen
Frequenzgenerator mit nachgeschaltetem Audioverstärker versorgt. Bei einer Primärspannung
von 37,3V und 7,018kHz stellte sich der optimale Betriebspunkt ein. CH1 zeigt die Spannung an
dem 15Ohm Lastwiderstand. CH2 zeigt die Primärspannung und CH3 den Primärstrom. Um die
Trafos ausreichend stark in die Sättigung zu steuern, war es notwendig, einen geringen
Gleichanteil der Spannung zu überlagern, weil die Ausgangsspannung des Verstärkers nicht
hoch genug war. Aus diesem Grund enthält der Primärstrom nur die negativen Halbwellen.
Die zugeführte Leistung beträgt 12,79W, am Lastwiderstand wird eine Leistung von 8,66W
umgesetzt. Somit ergibt sich auch für den Betrieb mit sinusförmiger Spannung ein beachtlicher
Wirkungsgrad von 67,7%.
Weitere Versuche
Eine Hoffnung hat sich allerdings nicht erfüllt. Der Wirkungsgrad blieb unter 100%. Im Internet
wird viel davon geschrieben, dass für die Änderung der Induktivität weniger Energie benötigt
wird, als letztendlich gewonnen werden kann. Obwohl das Schwingungsverhalten und die
gleichrichtende Wirkung sehr interessant ist, konnte bei diesem Modell kein Wirkungsgrad von
größer 100% gemessen werden. Der Laststrom wirkt sich sehr wohl auf den Eingang aus. Das ist
hauptsächlich dadurch begründet, dass der jeweils in Sättigung gebrachte Trafo quasi einen
Kurzschluss darstellt und sich so die Spannung am Ausgang, durch den Wegfall der
gegengerichteten Spannung, nicht mehr aufheben kann.
Wenn man etwas nicht kennt, ist man leicht dazu geneigt, es als unmöglich einzustufen, wenn es
einem in der Logik widerspricht. Das habe ich bemerkt, als ich das Modell vorführte. Unbekannt
sollte aber nicht mit unmöglich gleichgesetzt werden. Es ist schon allein wegen der riesigen
Informationsmengen nicht möglich alles zu wissen. Das soll aber nicht dazu führen, sich vor
dem neuen und unbekannten zu verschließen. Das Leben ist ein ständiger Lernprozess, der nie
aufhört. Doch gerade in der Technik erscheint alles so logisch und erklärbar, dass man leicht den
Eindruck bekommt, dass es nichts Neues und Unbekanntes mehr gibt.
Die parametrische Schwingungserregung findet sich auch in diesem
Buch, wo versucht wird, durch Grundlagenexperimente und neue
theoretische Ansätze mehr Licht in das Thema der Freien Energie zu
bringen. Nähere Informationen zum Buch.
Titel:
Grundlagen und Praxis der Freien Energie
Alternative Theorien und interessante Experimente
Autoren: Harald Chmela und Wolfgang Wiedergut
Verlag:
Erschienen im August 2004 im Franzis Verlag
ISBN
Nr.:
3-7723-4400-3
Elektrotechnikseite