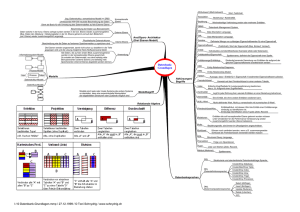
1. Organisatorisches und Datenmodellierung (Teil 1)
Werbung
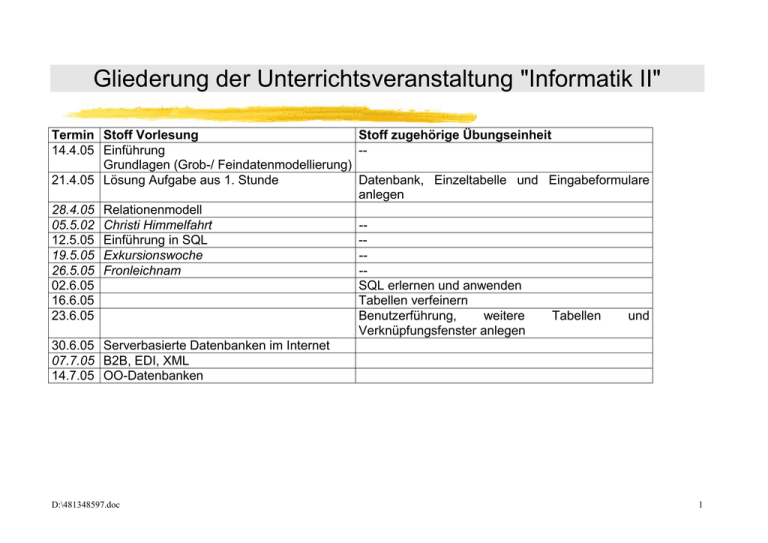
Gliederung der Unterrichtsveranstaltung "Informatik II" Termin Stoff Vorlesung Stoff zugehörige Übungseinheit 14.4.05 Einführung -Grundlagen (Grob-/ Feindatenmodellierung) 21.4.05 Lösung Aufgabe aus 1. Stunde Datenbank, Einzeltabelle und Eingabeformulare anlegen 28.4.05 Relationenmodell 05.5.02 Christi Himmelfahrt -12.5.05 Einführung in SQL -19.5.05 Exkursionswoche -26.5.05 Fronleichnam -02.6.05 SQL erlernen und anwenden 16.6.05 Tabellen verfeinern 23.6.05 Benutzerführung, weitere Tabellen und Verknüpfungsfenster anlegen 30.6.05 Serverbasierte Datenbanken im Internet 07.7.05 B2B, EDI, XML 14.7.05 OO-Datenbanken D:\481348597.doc 1 D:\481348597.doc 2 Datenmodellierung Grundelemente von Datenmodellen - Entitäten = welche Objekte sind betroffen (z.B. Touristen) - Beziehungen zwischen Entitäten (ein Unternehmen des Übernachtungsgewerbes kann einen oder mehrere Touristen aufnehmen) - Attribute zur Charakterisierung von Entitäten (Übernachtungsidentifikationsnummer, Datum der Übernachtung, Vergünstigung usw.) - Schlüssel (Übernachtungsidentifikationsnummer) D:\481348597.doc 3 Entitäten a) Eine Entität ist ein Element der Datenwelt, welches ein reales oder ein gedankliches Einzelphänomen in einem betrachteten Realitätsausschnitt repräsentiert (z.B. der Frühbuchungsrabatt, der Tourist 007 usw.). b) Eine Entitätsmenge (entity set) faßt alle Entitäten zusammen, die durch gleiche Merkmale, nicht notwendigerweise aber durch gleiche Merkmalsausprägungen, charakterisiert werden. (z.B. Beherbergungsbetriebe, ...). c) Graphische Darstellung: Beherbergungsbetriebe Touristen Beziehungen zwischen Entitäten Eine Assoziation a(E1, E2) gibt an, wieviele Entitäten der Entitätsmenge E2 einer beliebigen Entität der Entitätsmenge E1 zugeordnet sein können. D:\481348597.doc 4 In der Datenmodellierung gebräuchliche Assoziationstypen: Bezeichnung des Assoziationstyps A(E1, E2) einfach konditionell multipel multipel-konditionell D:\481348597.doc Symbol Anzahl der Entitäten in E2, die der Entität E1 zugeordnet werden können 1 c m mc genau eine keine oder eine, d.h. c=0 oder c=1 mindestens eine, d.h. m >=1 keine, eine oder mehrere, d.h. mc >=0 5 Attribute Ein Attribut beschreibt eine bestimmte Eigenschaft, die sämtliche Entitäten einer Entitätsmenge oder sämtliche Einzelbeziehungen einer Beziehung aufweisen. Der Wertebereich (domain) eines Attributs besteht aus der Menge der Datenwerte, die das Attribut für die Entitäten der zugrundeliegenden Entitätsmenge annehmen kann. Entitätsmenge Übernachtungsanbieter (4. Grades mit 2 Beispielstupeln) Attribute TourismusName Identifikation Entität 1 Entität 2 D:\481348597.doc 4657894 4658995 Art Kategorie Pension Garni Hirsch Frühstückspension einfach Bayerischer Hof Hotel gehoben Freising 6 Identifikationsschlüssel Der Unterschied zwischen zwei Entitäten einer Entitätsmenge drückt sich in unterschiedlichen Attributwerten aus. Zumindest für ein Attribut müssen zwei Entitäten unterschiedliche Werte annehmen, damit sie als individuelle Exemplare unterscheidbar sind. Ein Identifikationsschlüssel besteht aus einem Attribut oder aus einer Kombination von Attributen, welche jede Entität einer Entitätsmenge eindeutig identifiziert. Zu unterscheiden sind einfache und zusammengesetzte Identifikationsschlüssel. D:\481348597.doc 7 Entity Relationsship-Modell (Chen) Grundlegende Elemente: - Entitäten - Beziehungen - Rollen (roles = Funktionen, welche Entitäten in einer Beziehung erfüllen) Beispiele: zu Entitäten Übernachtungsanbieter Kunden zu Beziehungen n:m-Beziehung Übernachtungen zwischen Kunden und Übernachtungsanbieter, d.h.: Ein Kunde kann bei einem/mehreren Übernachtungsanbietern übernachten. Ein Übernachtungsanbieter bietet Übernachtungen für einen/mehrere Kunden an. zu Rollen Beispielsweise die Funktion "Vollpension" in der Beziehung Übernachtungen D:\481348597.doc 8 Schreibweise für Relationen Relationsname(Attribut1, Attribut2, Attribut3,...) Übernachtungsanbieter(TourismusID,Name,Art,Kategorie) - Die Anordnung der Attribute ist nicht signifikant (Da die Attribute durch Namen identifiziert werden). - Sämtliche Tupel sind gleichberechtigt; die Anordnung der Tupel einer Relation ist folglich ebenfalls nicht signifikant. - Identische Tupel treten nicht auf; zwei beliebige Tupel unterscheiden sich daher in mindestens einem Attributwert. - Daraus folgt: Es existieren stets ein oder mehrere Attribute, deren Werte jeden Tupel der Relation eindeutig identifizieren (=Schlüsselkandidat = candidate key). - Die Werte der Attribute sind atomar, d.h. ein Attribut nimmt in einer Relation genau einen Wert und nicht etwa eine Folge von Werten an. D:\481348597.doc 9 Behandlung netzwerkartiger Beziehungen Touristen mc mc Anbieter Umformung durch Einführung einer Hilfsrelation Touristen Anbieter 1 1 m mc Übernachtungen D:\481348597.doc 10