PDF_4

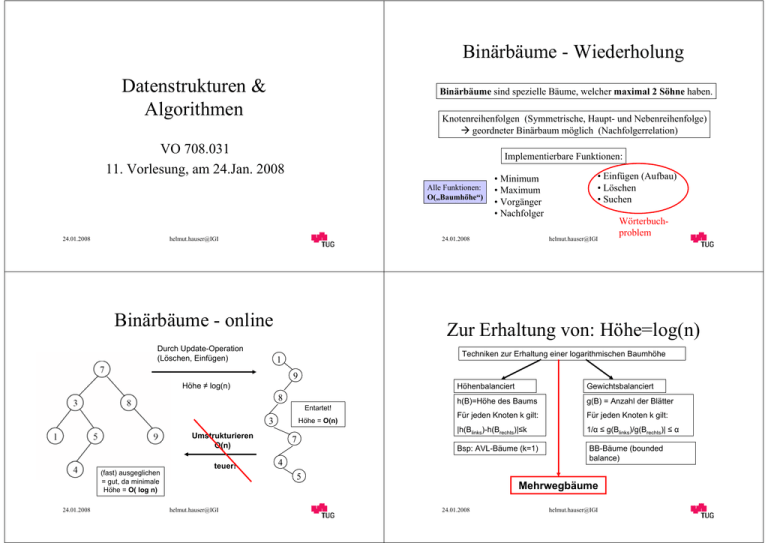
Binärbäume - Wiederholung
Datenstrukturen &
Algorithmen
Binärbäume sind spezielle Bäume, welcher maximal 2 Söhne haben.
Knotenreihenfolgen (Symmetrische, Haupt- und Nebenreihenfolge)
Æ geordneter Binärbaum möglich (Nachfolgerrelation)
VO 708.031
11. Vorlesung, am 24.Jan. 2008
Implementierbare Funktionen:
Alle Funktionen:
O(„Baumhöhe“)
24.01.2008
helmut.hauser@IGI
• Minimum
• Maximum
• Vorgänger
• Nachfolger
24.01.2008
Binärbäume - online
Durch Update-Operation
(Löschen, Einfügen)
• Einfügen (Aufbau)
• Löschen
• Suchen
helmut.hauser@IGI
Wörterbuchproblem
Zur Erhaltung von: Höhe=log(n)
Techniken zur Erhaltung einer logarithmischen Baumhöhe
1
9
Höhe ≠ log(n)
8
Entartet!
3
Höhe = O(n)
Umstrukturieren
O(n)
(fast) ausgeglichen
= gut, da minimale
Höhe = O( log n)
24.01.2008
teuer!
7
Höhenbalanciert
Gewichtsbalanciert
h(B)=Höhe des Baums
g(B) = Anzahl der Blätter
Für jeden Knoten k gilt:
Für jeden Knoten k gilt:
|h(Blinks)-h(Brechts)|≤k
1/α ≤ g(Blinks)/g(Brechts)| ≤ α
Bsp: AVL-Bäume (k=1)
4
5
helmut.hauser@IGI
BB-Bäume (bounded
balance)
Mehrwegbäume
24.01.2008
helmut.hauser@IGI
Definition:
(2-4)-Bäume
(2-4)-Bäume
Ein (2-4)-Baum ist ein Baum mit folgenden Eigenschaften:
Höhe=O(log n)
Enthalten nur
Hilfsinformationen.
4,6
(1) Alle Äste sind gleich lang.
(2) Die max. Anzahl der Söhne eines Knotens ist gleich 4.
1,2
10,11
5
(3) Innere Knoten haben ≥ 2 Söhne.
1
2
4
5
6
10
11
24
(4) Die Blätter enthalten v.l.n.r. die Werte aufsteigend sortiert.
(5) Jeder innere Knoten mit t Söhnen (2 ≤ t ≤ 4) speichert t-1
Hilfsinformationen x1, …, xt-1, wobei xi = größter Wert im Teilbaum
des i-ten Sohnes von links.
24.01.2008
helmut.hauser@IGI
Daten werden in den Blättern gespeichert.
24.01.2008
helmut.hauser@IGI
(2-4)-Bäume
(2,4)-Bäume - Suchen
Wir wollen damit das Wörterbuchproblem lösen:
8
11
SUCHEN, EINFÜGEN, ENTFERNEN
Achtung:
Nach den Update-Funktionen (Einfügen, Entfernen)
muss wieder ein korrekter 2-4-Baum vorliegen !
2
2
4
4
5
5
10
8
10
12
11
siehe später
helmut.hauser@IGI
24
Pro Knoten maximal 3 Vergleich Æ O(1)
Æ Höhe garantiert Θ(log n) Æ T(n)=Θ(log n)
Æ Zeitlicher Mehraufwand, der sich aber rentiert Æ Amortisierte Kosten
24.01.2008
12
24
24.01.2008
helmut.hauser@IGI
31
(2,4)-Bäume - Einfügen
(2,4)-Bäume - Entfernen
Zwei Fälle (nach dem Entfernen):
Definition:
1.) Falls α(k) ≥ 2 Æ fertig !!
α(k) ist die Ordnung des k-ten Knoten (=Anzahl der Söhne)
2.) Falls α(k) < 2 Æ Bedingung verletzt (underflow) Æ
Zwei Fälle (nach! dem Einfügen):
STEHLEN (wenn α(k‘) ≥ 3)
oder VERSCHMELZEN (α(k‘) = 2)
1.) Falls α(k) ≤ 4 Æ fertig !!
k’
2.) Falls α(k) > 4 Æ Bedingung verletzt Æ SPALTEN
v
v
24.01.2008
helmut.hauser@IGI
Analyse der Operationen
k’
k’
O(log n)
O(log n)
O(log n)
Speicher:
O(n)
k’
VERSCHMELZEN
Mischbare Warteschlangen
Definition:
•
•
•
•
EINFÜGEN (S,x)
MAXIMUM (S)
ENTFERNE_MAX (S)
MISCHE (S,S‘)
Halde Æ 3 Operationen in O(log n)
Mit Baum alle Operation Æ O(log n)
helmut.hauser@IGI
k
helmut.hauser@IGI
Mischen aber teuer !! Æ O(n)
24.01.2008
k
v
k
24.01.2008
Wörterbuchproblem
Suchen:
Einfügen:
Entfernen:
STEHLEN
v
v’
k
k
k
24.01.2008
helmut.hauser@IGI
Mischbare Warteschlangen
9
3
3
9
1
9
8
5
2
6
Mischbare Warteschlangen
-Unsortierter (2,4)-Baum
Mische (S, S‘): Æ Beides 2-4-Bäume mit der Höhe h und h‘
- innere Knoten speichert
Maximum in seinen Teilbaum
und Zeiger darauf
1.Fall: h = h‘
2.Fall: h > h‘
Neue Wurzel = O(1)
Check α(v) Æ O(log n)!!
8
Entferne Maximum Æ Update der
Information O(log n)
Maximum trivial Æ
in Wurzel O(1)
v
k
w’
8
h’
Einfügen ist
Spezialfall von
Mischen!
5
3
24.01.2008
T
8
1
5
2
6
T’
8
helmut.hauser@IGI
24.01.2008
helmut.hauser@IGI
Amortisierte Kosten
2-4-Bäume benötigen zusätzliche Operation, damit sie 2-4-Bäume
bleiben und damit garantiert h=O(log n) besitzen.
Danke für Ihre Aufmerksamkeit!
Bis zum nächsten Mal.
Potentielle Laufzeit:
O(m*log(n))
( Donnerstag, 31.Jan.2008, i13 )
Beobachtung: z.B. nach Spalt-Operation ist der Baum „ausgeglichener“.
Æ Investierte Zeit rentiert sich später Æ Amortisierungsanalyse.
Durchschnittliche Zeit über alle Operation
(in unserem Fall: Einfügen, Löschen) im schlimmsten Fall.
24.01.2008
helmut.hauser@IGI
24.01.2008
helmut.hauser@IGI