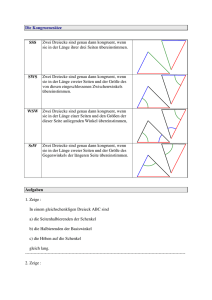
Übungen zur Kongruenz und Konstruktionen

Werdenfels – Gymnasium – 2011/2012
Vermischte Aufgaben
1. Zeichne für jede Teilaufgabe jeweils eine nichtmaßstabsgereue Skizze des ∆ABC
und des ∆A1 B1 C1 . Trage übereinstimmende Stücke mit gleicher Farbe in dies
Skizzen ein und entscheide, ob sie kongruent sind. Gib ggf. den entsprechneden
Kongruenzssatz an.
a) c = b1 , a = c1 und b = a1 .
b) b = c1 , α = γ1 und γ = β1
c) b = c1 , c = a1 und α = β1
d) a = b1 , γ = γ1 und α = β1
e) c = c1 , b = a1 und γ = γ1 .
Außerdem gilt c > b und c1 > a1
2. ∆ABC ist ein gleichschenklige Dreieck. D ist ein Punkt auf der Basis AB. Dadurch
entstehen die Dreiecke ∆ADC und ∆BDC.
a) Zeichne eine sorgfältige, nicht maßstabsgetreue Skizze, die dem obigen Sachverhalt Rechnung trägt.
b) ∆ACD und ∆BDC stimmen in drei Stücken überein. Finde sie heraus und
begründe, warum diese beiden Teildreiecke im allgemeinen nicht kongruent
sind.
c) Was muss D für ein spezieller Punkt sein, damit die beiden Teildreiecke kongruent sind. Begründe deine Aussage sorgfältig.
3. Fertige für jede Teilaufgabe eine Planzeichnung, die Konstruktion und einen Konstruktionsplan an.
a) a = 6,0 cm, b = 5, cm und c = 7,5 cm
b) b = 9 cm, c = 6 cm und α = 65◦
c) c = 7 cm, α = 80◦ und β = 40◦
d) a = 4 cm, b = 7 cm und c = 9,5 cm.
e) a = 4,5 cm, b = 6,5 cm und γ = 70◦
f) c = 5 cm, α = 30◦ und γ = 20◦
g) b = 5,5 cm, β = 45◦ und γ = 70◦
4. Bei einem gleichschenkligen Dreieck ∆ABC ist der Winkel an der Spitze C um
30% größer als ein Basiswinkel.
Berechne die Größe der Innenwinkel α, β und γ.
1
Werdenfels – Gymnasium – 2011/2012
5. Begründe, dass in einem gleichschenkligen Dreieck ∆ABC mit der Basis c die
Winkelhalbierenden auf die Schenkel gleichlang sind.
Aufgaben zum Begründen
1. Begründe durch Kongruenz, dass die Symmetrieachse eines gleichschenkligen Dreiecks dieses in zwei kongruente Teildreiecke zerlegt.
2. Ein Drachenviereck ist ein achsensymmetrisches Viereck.
a) Zeichne das Drachenviereck ABCD.
b) Zeige, dass die Symmetrieachse das Drachenviereck ABCD in zwei kongruente
Teildreiecke zerlegt.
3. Begründe, dass ein rechtwinkliges und ein gleichseitiges Dreieck nicht kongruent
sein können.
4. Begründe die richtigen Aussagen mit Hilfe von Kongruenzssätzen und gib zu den
falschen Aussagen jeweils ein Gegenbeispiel an:
a) Alle gleichseitigen Dreiecke mit gleichlanger Seite sind zueinander kongruent.
b) Alle rechtwinkligen Dreiecke mit einem 30◦ Winkel sind zueinander kongruent.
c) Alle gleichschenkligen Dreiecke, die in einer Seitenlänge und einem Winkel
übereinstimmen sind kongruent.
d) Alle rechtwinkligen Dreiecke mit zwei gleichlangen Seiten sind zueinander
kongruent.
Aufgaben zum Konstruieren
Allgemeiner Hinweis:
Fertige für jede Konstruktion eine sorgfältige Planskizze an, in die du alle gegebenen
Stücke einträgst. Führe die Konstruktion nur mit Zirkel, Lineal und gespitzen Bleistift
an. Erstelle im Anschluss an die Konstruktion einen mathematisch formulierten Konstruktionsplan.
1. rechtwinklige Dreiecke:
a) Konstruiere ein rechtwinkliges Dreieck mit der Hypothenuse 5 cm und α =
40◦ .
b) Konstruiere ein gleichschenklig- rechtwinkliges Dreieck ABC mit der Hypothenuse c = 6 cm.
c) Konstruiere ein ∆ABC mit γ = 90◦ und c = 6 cm
2
Werdenfels – Gymnasium – 2011/2012
2. Knifflige Dreieckskonstruktionen
a) Konstruiere das Dreieck ∆ABC aus c = 5 cm, ha = 3 cm und α = 40◦ .
b) Konstruiere ein ∆ABC aus c = 4 cm, sa = 3 cm und β = 50◦ .
c) Konstruiere ein Dreieck ∆ABC aus b = 5 cm, hc = 3 cm und α = 40◦
3. Gleichschenklige Dreiecke
a) Konstruire ein gleichschenkliges Dreieck ∆ABC mit der Basis a = 6 cm und
dem Basiswinkel γ = 35◦
b) Konstruiere ein gleischenkliges Dreieck aus der Basis c = 5 cm, hb = 3 cm.
c) Konstruiere ein gleichschenkliges Dreieck ∆ABC aus c = b = 4 cm und α =
30◦ .
4. Tangentenkonstruktionen
a) Zeichne in ein Koordinatensystem die Punkte P (−3|2) und M (2| − 2) ein.
Zeichne k(M ; r = 3 cm und konstruiere die Tangenten an diesen Kreis, die
durch den Punkt P verlaufen.
b) Zeichne den Punkt P (4|2) und A(−3|2) in ein Koordinatensystem ein. A
ist ein Berührpunkts der Tangente an einen Kreis mit Radius r = 3 cm.
Konstruiere den Mittelpunkt dieses Kreises.
3