Die Kongruenzsätze SSS Zwei Dreiecke sind genau dann

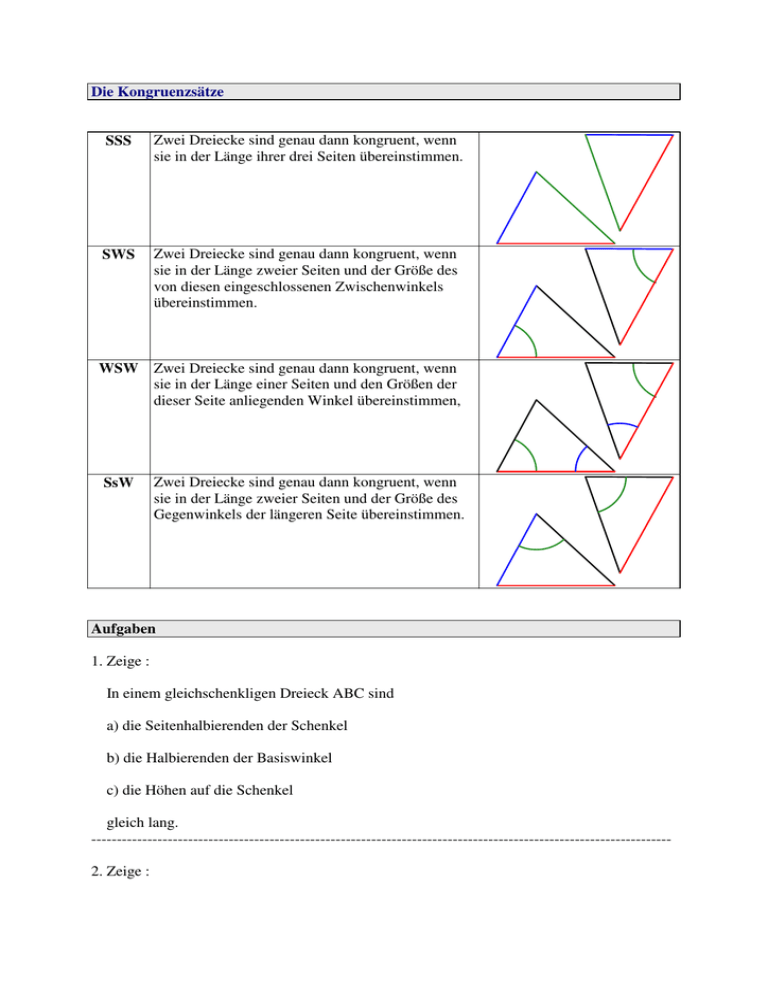
Die Kongruenzsätze
SSS
Zwei Dreiecke sind genau dann kongruent, wenn
sie in der Länge ihrer drei Seiten übereinstimmen.
SWS
Zwei Dreiecke sind genau dann kongruent, wenn
sie in der Länge zweier Seiten und der Größe des
von diesen eingeschlossenen Zwischenwinkels
übereinstimmen.
WSW Zwei Dreiecke sind genau dann kongruent, wenn
sie in der Länge einer Seiten und den Größen der
dieser Seite anliegenden Winkel übereinstimmen,
SsW
Zwei Dreiecke sind genau dann kongruent, wenn
sie in der Länge zweier Seiten und der Größe des
Gegenwinkels der längeren Seite übereinstimmen.
Aufgaben
1. Zeige :
In einem gleichschenkligen Dreieck ABC sind
a) die Seitenhalbierenden der Schenkel
b) die Halbierenden der Basiswinkel
c) die Höhen auf die Schenkel
gleich lang.
-----------------------------------------------------------------------------------------------------------------2. Zeige :
Ein Punkt auf der Winkelhalbierenden eines Winkels ist von den Schenkeln des Winkels
gleich weit entfernt.
-----------------------------------------------------------------------------------------------------------------1. Konstruiere ein Dreieck ABC aus
a) β = 60°, wβ = 4 cm und a = 7 cm
b) a = 7 cm, b = 8 cm und sb = 6 cm
c) α = 90°¦, wα = 4 cm und β = 60°
d) c = 10 cm, hc = 4 cm und sc = 5 cm
e) a = 5 cm, β = 40° und b = 4 cm
f) Umkreisradius ρ = 4 cm, a = 7,5 cm und ha = 1,5 cm
-----------------------------------------------------------------------------------------------------------------2. Konstruiere ein gleichschenkliges Dreieck ABC mit der Basis AB aus
 
a) a = 6 cm und hc = 4 cm
b) γ = 105° und hc = 3,5 cm
c) β = 75° und hc = 4 cm
d) a = 8 cm und β = 30°
e) c = 5 cm und ha = 4 cm
-----------------------------------------------------------------------------------------------------------------3. Konstruiere ein gleichseitiges Dreieck ABC mit
a) h = 5 cmh=5cm
b) Umkreisradius r = 3 cm
c) Inkreisradius ρ = 1,5 cm?=1.5cm
-----------------------------------------------------------------------------------------------------------------4. Von einem gleichschenkligen Dreieck sind die Symmetrieachse; ein auf der Basis liegender
und jeweils ein auf den Schenkeln liegender Punkt gegeben.
Wie lässt sich das Dreieck konstruieren.
-----------------------------------------------------------------------------------------------------------------5. Konstruiere ein Rechteck mit
a) a = 4 cm und e = AC = 5 cm
b) dem Umkreisradius r = 4 cm und einem Schnittwinkel der Diagonalen von 60°.
-----------------------------------------------------------------------------------------------------------------6. Konstruiere ein gleichschenkliges Trapez (ABhCD) mit
a) a = 7 cm, b = 5 cm und c = 3 cm
b) a = 8 cm, β = 60° und b = 2 cm
c) a = 5 cm, h = 1,5 cm und e = AC = 4 cm
d) a = 4 cm, β = 120° und e = AC = 7 cm
-----------------------------------------------------------------------------------------------------------------7. Konstruieren eine Raute mit
a) e = 7,8 cm und f = 4,2 cm
b) a = 2,8 cm und α = 45°
c) a = 6 cm und e = 8 cm
-----------------------------------------------------------------------------------------------------------------8. Konstruiere ein ein Drachenviereck (Symmetrieachse AC) mit
a) a = 3,6 cm, b = 4,8 cm und f = 5 cm
b) a = 3 cm, b = 4 cm und α = 60°
c) c = 3 cm, β = 90° und e = 7 cm
-----------------------------------------------------------------------------------------------------------------9. Konstruiere ein Quadrat mit
a) der Diagonale d = 5 cm
b) dem Inkreisradius ρ = 1,5 cm=1.5cm
-----------------------------------------------------------------------------------------------------------------10. Konstruiere ein Parallelogramm mit
a) a = 5 cm, b = 3 cm und e = 6 cm
b) α = 40°, ha = 3 cm und hd = 2 cm
-----------------------------------------------------------------------------------------------------------------11. Ein Parallelogramm liegt in einem Streifen der Breite 3cm. Die eine Diagonale misst 7cm
und schneidet die andere unter einem Winkel von ε = 70°.
Konstruiere das Parallelogramm.
------------------------------------------------------------------------------------------------------------------
12. Von einem Parallelogramm kennt man drei Seitenmittelpunkte Ma, Mb und Mc.
Wie lässt sich das Parallelogramm konstruieren ?
___________________________________________________________________________