Datenstrukturen

Datenstrukturen
Mariano Zelke
Sommersemester 2012
Graphen
(Link)
(a) Ein ungerichteter Graph G = (V , E ) besteht aus einer endlichen
Menge
und einer Teilmenge
V von Knoten (engl.: vertices)
E ⊆ {u, v } u, v ∈ V , u 6= v von Kanten (engl.: edges).
I
I
Die Endpunkte u, v einer ungerichteten Kante {u, v } sind
gleichberechtigt.
u und v heißen dann Nachbarn.
Wir sagen auch: u und v sind adjazent.
(b) Für die Kantenmenge E eines gerichteten Graphen G = (V , E ) gilt
E ⊆ {(u, v ) | u, v ∈ V , u 6= v }.
I
I
Mariano Zelke
Der Knoten u ist Anfangspunkt und der Knoten v Endpunkt der
Kante (u, v ).
v heißt auch ein direkter Nachfolger von u und u ein direkter
Vorgänger von v .
Datenstrukturen
2/18
Wichtige Begriffe
Sei G = (V , E ) ein gerichteter oder ungerichteter Graph.
I
Eine Folge (v0 , v1 , ..., vm ) heißt ein Weg in G ,
falls für jedes i (0 ≤ i < m) gilt
I
I
(vi , vi+1 ) ∈ E (für gerichtete Graphen) bzw.
{vi , vi+1 } ∈ E (für ungerichtete Graphen).
Die Weglänge ist m, die Anzahl der Kanten. Ein Weg heißt einfach,
wenn kein Knoten zweimal auftritt.
I
Ein Weg heißt ein Kreis, wenn v0 = vm und (v0 , ..., vm−1 ) ein
einfacher Weg ist. G heißt azyklisch, wenn G keine Kreise hat.
I
Ein ungerichteter Graph heißt zusammenhängend, wenn je zwei
Knoten durch einen Weg miteinander verbunden sind.
Mariano Zelke
Datenstrukturen
3/18
Das Königsberger Brückenproblem
1
2
3
4
Mariano Zelke
Datenstrukturen
4/18
Graph-Implementierungen
I
I
Welche Datenstruktur sollten wir für die Darstellung
eines Graphen G wählen?
Welche Operationen sollen schnell ausführbar sein?
I
I
Ist e eine Kante von G ? Die Adjazenzmatrix wird sich als eine gute
Wahl herausstellen.
Bestimme die Nachbarn, bzw. Vorgänger und Nachfolger eines
Knoten: Die Adjazenzlistendarstellung ist unschlagbar.
Besonders die Nachbar- und Nachfolgerbestimmung ist wichtig, um
Wege zu durchlaufen.
Mariano Zelke
Datenstrukturen
5/18
Die Adjazenzmatrix
Für einen Graphen G = (V , E ) (mit V = {0, ..., n − 1}) ist
1
wenn {u, v } ∈ E (bzw. wenn (u, v ) ∈ E ),
AG [u, v ] =
0
sonst
die Adjazenzmatrix AG von G .
Eine Kantenfrage ist (u, v ) eine Kante?“ wird sehr schnell
”
beantwortet, nämlich in Zeit O(1).
Die Bestimmung aller Nachbarn oder Nachfolger eines Knoten v ist
hingegen langwierig:
I
I
Die Zeile von v muss durchlaufen werden.
Zeit Θ(n) selbst dann, wenn v nur wenige Nachbarn hat.
Speicherplatzbedarf Θ(n2 ) auch für Graphen mit relativ wenigen
Kanten:
Die Datenstruktur passt sich nicht der Größe des Graphen an!
Mariano Zelke
Datenstrukturen
6/18
Die Adjazenzliste
G wird durch ein Array A von Listen dargestellt.
Die Liste A[v ] führt alle Nachbarn von v auf, bzw. alle Nachfolger von v
für gerichtete Graphen.
Die Nachbar- bzw. Nachfolgerbestimmung für Knoten v gelingt in
Zeit proportional zur Anzahl der Nachbarn oder Nachfolger.
Der benötigte Speicherplatz ist O(n + |E |): Die Datenstruktur passt
sich der Größe des Graphen an.
Für die Beantwortung der Kantenfrage ist (u, v ) eine Kante?“
”
muss die Liste A[u] durchlaufen werden: Die benötigte Zeit ist also
proportional zur Anzahl der Nachbarn oder Nachfolger.
Da die Nachbar- bzw. Nachfolgerbestimmung für das Durchlaufen von
Wegen benötigt wird, ist die sich der Größe des Graphen anpassende
Adjazenzliste oft die Datenstruktur der Wahl.
Mariano Zelke
Datenstrukturen
7/18
Suche in Graphen
Wie durchsucht man ein Labyrinth?
I
Können wir das Preorder-Verfahren benutzen?
I
I
I
Preorder terminiert nicht, wenn ein ungerichteter Graph einen Kreis
besitzt: Preorder erkennt nicht, dass es Knoten bereits besucht hat!
Um Preorder anzupassen, sollten wir für jeden Knoten v vermerken,
ob v bereits besucht wurde.
Wir erhalten Tiefensuche = Preorder + Knotenmarkierung“.
”
Mariano Zelke
Datenstrukturen
8/18
Tiefensuche: Die globale Struktur
I
Der gerichtete oder ungerichtete Graph G werde durch seine
Adjazenzliste A repräsentiert.
I
Im Array besucht wird vermerkt, welche Knoten bereits besucht
wurden.
void Tiefensuche(){
for (int k = 0; k < n; k++) besucht[k] = 0;
for (int k = 0; k < n; k++)
if (! besucht[k])
tsuche(k);
}
I
Jeder Knoten wird besucht,
I
aber tsuche(v) wird nur dann aufgerufen, wenn v nicht als
besucht“ markiert ist.
”
Mariano Zelke
Datenstrukturen
9/18
tsuche()
Die Knoten des Graphen werden definiert durch
struct Knoten {
int name;
Knoten *next; }
I
Als erste Aktion von tsuche(v) wird v als besucht markiert.
I
Dann wird tsuche(v) für alle unmarkierten Nachbarn/Nachfolger
von v rekursiv aufgerufen.
void tsuche(int v){
besucht[v] = 1;
Knoten *p;
for (p = A[v]; p !=0; p = p->next)
if (!besucht [p->name])
tsuche(p->name);
}
Mariano Zelke
Datenstrukturen
10/18
Der Wald der Tiefensuche: ungerichtete Graphen
Wir veranschaulichen das Vorgehen von Tiefensuche.
I
Eine Kante {v , w } ∈ E heißt eine Baumkante, falls tsuche(w) in der
Schleife von tsuche(v) aufgerufen wird.
I
Eine Kante {v , w } ∈ E heißt eine Rückwärtskante, falls {v , w }
keine Baumkante ist und tsuche(w) während der Ausführung von
tsuche(v) aufgerufen wird.
Die Baumkanten definieren einen Wald, den wir den Wald der
Tiefensuche nennen.
I
I
Wir können uns die (eigentlich ungerichteten) Kanten von WG auch
gerichtet vorstellen, jede Kante in WG vom früher zum später
markierten Knoten gerichtet. Dann können wir in WG von
Nachfolgern, Nachfahren, Vorgängern und Vorfahren sprechen.
Sind alle Kanten des Graphen entweder Baum- oder Rückwärtskanten?
Mariano Zelke
Datenstrukturen
11/18
Tiefensuche: Beispiel
(und noch eins hier)
@ Nordturm
V
@
A 54
V53
A V55@
@
H
H
B
B
V35 A
V17
V52
V32 B
B
H
@ H
H
H @
B
@
@ V51
@ V B V1
V
@
@ 16 B
@P 31
PP V @
PP 15 @
P
P
V30
Ostturm
V37
V36 @
@
A V38 @
@
H
H
@
@
@
@ V
@
@
@
@
@
@
V18
@
39
@
@
@
@
@
@
@
@
@
V19
H
H
@ V40
V2
V3 A H
H V20 @
@
@
A V4 @
@
@
V14
V0
V5
V21
V6
V22
Innenhof
V29
V13
@
@
@
A V12
@
H
H V
11
V
@
@ 28
V50 @
V10
@
@
@ V27 V49
@
V34 @
V26
@
@
V46
@ V48 @
@
V
47
@
@
Westturm
Mariano Zelke
P
P
PP
P
@
@ V7 PP
B
@
@
V23
B V8 V41@
P
V9 B
PP
@
@
P @
@
BB V24
V42
B
V33
V25
B
H
B
H
@ V45 BB
V43
@
A
V44
@
Südturm @
Datenstrukturen
12/18
Tiefensuche: Beispiel
(und noch eins hier)
54
53
52
37
55
35
51
17
18
19
16
1
2
3
0
4
20
30
14
5
21
29
13
6
22
28
12
7
23
34
11
10
9
8
27
26
25
24
46
47
41
33
45
Datenstrukturen
39
40
15
48
Mariano Zelke
32
38
31
50
49
36
42
43
44
12/18
Tiefensuche: Beispiel
(und noch eins hier)
54
53
52
37
55
35
51
Baumkante
Rückwärtskante
17
18
19
16
1
2
3
0
4
20
30
14
5
21
29
13
6
22
28
12
7
23
34
11
10
9
8
27
26
25
24
46
47
41
33
45
Datenstrukturen
39
40
15
48
Mariano Zelke
32
38
31
50
49
36
42
43
44
12/18
Tiefensuche: Beispiel
(und noch eins hier)
54
53
52
37
55
35
51
Wald der
Tiefensuche:
17
18
19
16
1
2
3
0
4
20
30
14
5
21
29
13
6
22
28
12
7
23
34
11
10
9
8
27
26
25
24
46
47
41
33
45
Datenstrukturen
39
40
15
48
Mariano Zelke
32
38
31
50
49
36
42
43
44
12/18
Tiefensuche für ungerichtete Graphen I
Sei G = (V , E ) ein ungerichteter Graph und {v , w } sei eine Kante von
G . WG sei der Wald der Tiefensuche für G .
(a) tsuche(v ) werde vor tsuche(w ) aufgerufen. Dann ist w ein
Nachfahre von v in WG .
(b) G besitzt nur Baum- und Rückwärtskanten.
(a) Warum ist w ein Nachfahre von v in WG ?
I
I
I
tsuche(v ) wird vor tsuche(w ) aufgerufen: Knoten w ist zum
Zeitpunkt der Markierung von Knoten v unmarkiert.
tsuche(v ) kann nur dann terminieren, wenn w markiert wird.
w muss irgendwann während der Ausführung von tsuche(v) markiert
werden.
(b) Warum besitzt G nur Baum- und Rückwärtskanten? Wenn {v , w }
eine Kante ist, dann ist v Vorfahre oder Nachfahre von w .
Mariano Zelke
Datenstrukturen
13/18
Tiefensuche für ungerichtete Graphen II
Tiefensuche besucht jeden Knoten genau einmal.
I
Das Programm Tiefensuche wird von einer Schleife gesteuert, die
tsuche(v) für alle noch nicht besuchten Knoten v aufruft.
I
Wenn aber tsuche(v) aufgerufen wird, dann wird v sofort markiert:
Nachfolgende Besuche sind ausgeschlossen.
Der Baum von v in WG enthält genau die Knoten der
Zusammenhangskomponente von v in G . Die Bäume von WG
entsprechen genau den Zusammenhangskomponenten von G .
I
T sei ein Baum im Wald WG und T besitze v als Knoten.
I
v erreicht jeden Knoten in T , denn T ist zusammenhängend.
Also ist die Zusammenhangskomponente von v in G eine Obermenge der
Knotenmenge von T .
I
Wenn v = v0 , v1 , . . . , vs = u ein Weg in G ist, dann gehören v0 , v1 , . . . , vs
zum selben Baum von WG . Die Komponente von v ist also auch eine
Untermenge der Knotenmenge von T . Also sind sie gleich.
Mariano Zelke
Datenstrukturen
14/18
Labyrinthe
Tiefensuche löst jedes Labyrinth-Problem, das sich als ungerichteter
Graph interpretieren lässt.
I
Wenn es möglich ist, vom Eingang den Ausgang zu erreichen, dann
befinden sich Eingang und Ausgang in derselben
Zusammenhangskomponente.
I
Dann besitzt der Baum in WG mit dem Eingangsknoten einen Weg
von Eingangs- zum Ausgangsknoten.
Wie schnell findet man aus einem Labyrinth heraus?
Wie schnell ist Tiefensuche?
Mariano Zelke
Datenstrukturen
15/18
Die Laufzeit von Tiefensuche
Tiefensuche terminiert nach höchstens O(|V | + |E |) Schritten.
I
Zuerst muss der Aufwand für die Schleife in Tiefensuche bestimmt
werden: O(n) Schritte.
I
Wie viele Schritte werden direkt von tsuche(v) ausgeführt?
O(grad(v )) Operationen, wobei grad(v ) die Anzahl der Nachbarn
von v ist.
I
Wie viele Operationen werden insgesamt ausgeführt?
X
X
X
O(
(1 + grad (v ) ) = O(
1+
grad (v ))
v ∈V
v ∈V
v ∈V
= O(|V | + |E |).
Tiefensuche ist sehr schnell.
Mariano Zelke
Datenstrukturen
16/18
Anwendungen der Tiefensuche
Sei G = (V , E ) ein ungerichteter Graph. Dann kann in Zeit O(|V | + |E |)
überprüft werden,
(a) ob G zusammenhängend ist:
I
I
I
G ist genau dann zusammenhängend, wenn G genau eine
Zusammenhangskomponente hat.
Die Bäume von WG entsprechen genau den
Zusammenhangskomponenten von G .
G ist also genau dann zusammenhängend, wenn WG aus genau
einem Baum besteht, d.h. wenn tsuche(0) alle Knoten besucht.
(b) ob G ein Wald ist:
I
I
Mariano Zelke
G ist genau dann ein Wald, wenn G keine Rückwärtskanten hat.
Überprüfe, dass für jede Kante {v , w } entweder tsuche(w) direkt in
tsuche(v) aufgerufen wird oder dass tsuche(v) direkt in tsuche(w)
aufgerufen wird.
Datenstrukturen
17/18
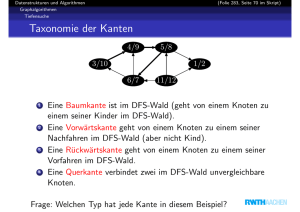
Tiefensuche für gerichtete Graphen I
Wald der
Tiefensuche:
0
1
2
4
0
1
3
4
2
3
Angenommen, die Tiefensuche startet im Knoten 0 und in jeder
Adjazenzliste sind die Knoten aufsteigend sortiert. Dann erhalten wir vier
verschiedene Kantentypen:
I
I
I
I
Baumkanten: (0, 1), (0, 2) und (2, 3), sie bilden den Wald WG der
Tiefensuche
Rückwärtskante: (3, 0), sie verbindet einen Knoten mit seinem
Vorgänger in WG
Querkanten: (3, 1) und (4, 2), sie verbinden zwei Knoten, die in WG
nicht miteinander in einer Nachfolger-Vorgänger-Beziehung stehen.
Vorwärtskante: (0, 3), sie verbindet einen Knoten mit einem
Nachfahren in WG , der kein Kind ist.
Mariano Zelke
Datenstrukturen
18/18