Tutoriumsaufgaben 1. Zwei Holzkugeln verschiedener Masse m1
Werbung
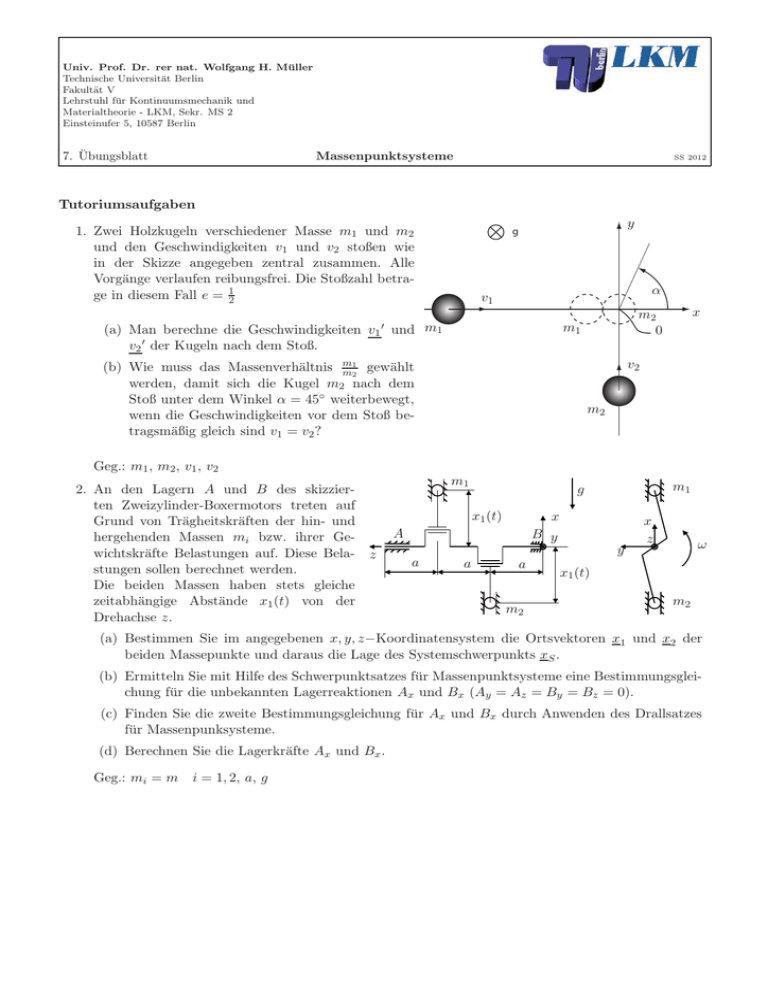
Univ. Prof. Dr. rer nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 7. Übungsblatt Massenpunktsysteme SS 2012 Tutoriumsaufgaben 1. Zwei Holzkugeln verschiedener Masse m1 und m2 und den Geschwindigkeiten v1 und v2 stoßen wie in der Skizze angegeben zentral zusammen. Alle Vorgänge verlaufen reibungsfrei. Die Stoßzahl betrage in diesem Fall e = 12 y g α v1 (a) Man berechne die Geschwindigkeiten v1 ′ und m1 v2 ′ der Kugeln nach dem Stoß. x m2 0 m1 v2 m1 gewählt (b) Wie muss das Massenverhältnis m 2 werden, damit sich die Kugel m2 nach dem Stoß unter dem Winkel α = 45◦ weiterbewegt, wenn die Geschwindigkeiten vor dem Stoß betragsmäßig gleich sind v1 = v2 ? m2 Geg.: m1 , m2 , v1 , v2 2. An den Lagern A und B des skizzierten Zweizylinder-Boxermotors treten auf Grund von Trägheitskräften der hin- und hergehenden Massen mi bzw. ihrer Gewichtskräfte Belastungen auf. Diese Bela- z stungen sollen berechnet werden. Die beiden Massen haben stets gleiche zeitabhängige Abstände x1 (t) von der Drehachse z. m1 m1 g x1 (t) x A B y y a a a m2 x z ω x1 (t) m2 (a) Bestimmen Sie im angegebenen x, y, z−Koordinatensystem die Ortsvektoren x1 und x2 der beiden Massepunkte und daraus die Lage des Systemschwerpunkts xS . (b) Ermitteln Sie mit Hilfe des Schwerpunktsatzes für Massenpunktsysteme eine Bestimmungsgleichung für die unbekannten Lagerreaktionen Ax und Bx (Ay = Az = By = Bz = 0). (c) Finden Sie die zweite Bestimmungsgleichung für Ax und Bx durch Anwenden des Drallsatzes für Massenpunksysteme. (d) Berechnen Sie die Lagerkräfte Ax und Bx . Geg.: mi = m i = 1, 2, a, g Univ. Prof. Dr. rer nat. Wolfgang H. Müller Technische Universität Berlin Fakultät V Lehrstuhl für Kontinuumsmechanik und Materialtheorie - LKM, Sekr. MS 2 Einsteinufer 5, 10587 Berlin 7. Übungsblatt Massenpunktsysteme SS 2012 Hausaufgaben 3. Zwei Autos stoßen unter einem Winkel α zusammen und rutschen ineinander verkeilt (ohne Rotation) nach dem Zusammenstoß mit blockierten Rädern eine Strecke XR , bis sie zum Stillstand kommen. XR m1 β α Geg.: • Massen und Geschwindigkeitsbeträge der Autos vor dem Zusammenstoß: m1 , v1 , m2 und v2 m2 • Reibbeiwert beim Rutschen µ • Winkel vor dem Stoß α (a) In welche Richtung rutschen die Autos nach dem Zusammenstoß? (b) Wie lang ist die Rutschstrecke XR ? (c) Ein Golf m1 = 1000kg und ein Mercedes m2 = 2000kg stoßen unter α = 45◦ zusammen. Der Golf hat seine Bewegungsrichtung beim Zusammenprall um β = 30◦ geändert. Aus der Rutschstrecke konnte die Geschwindigkeit der ineinander verkeilten Autos unmittelbar nach dem Zusammenstoß bestimmt werden, sie betrug 20 ms . Wie schnell waren die Autos vor dem Zusammenstoß? 4. Das dargestellte System besteht aus einer Punktmasse m, die auf einem Klotz 1 der Masse M1 liegt. Zwischen der Punktmasse und Klotz 1 wirkt der Gleitreibungskoeffizient µ, die Unterlage sei reibungsfrei. Klotz 1 ist über ein undehnbares massloses Seil und eine masselose Rolle mit einem weiteren Klotz 2 der Masse M2 verbunden. Das System wird zum Zeitpunkt t = 0 losgelassen und setzt sich derart in Bewegung, daß die Masse auf dem Klotz 1 zu gleiten beginnt. Nach der Zeit t∗ schlägt der Klotz 2 auf den Boden auf. µ m Punktmasse g reibungsfrei M1 M2 Klotz 1 Klotz 2 h ∗ der Punktmasse und v ∗ des Bestimmen Sie mit Hilfe des Impulssatzes die Geschwindigkeit vm M ∗ Klotzes 1 zum Zeitpunkt t , an dem Klotz 2 auf den Boden aufprallt. q Geg.: g, m, M1 = M2 = 52 m, µ = 15 , t∗ = 2 2 hg


