Die Arbeitspunkteinstellung beim Bipolartransistor
Werbung

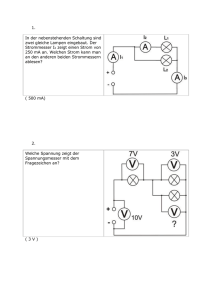
Die Arbeitspunkteinstellung beim Bipolartransistor In der Schaltungstechnik stellt sich immer wieder das Problem der Arbeitspunkteinstellung eines Bipolartransistors (BJT). Bauteiltoleranzen des Transistors und der Temperaturbereich, in welcher die Schaltung ihre Eigenschaften beibehalten soll, erschweren die Aufgabenstellung. Im Folgenden wird eine Berechnungsmethode vorgestellt, mit welcher der Autor ausgezeichnete Erfahrungen gemacht hat. Es ist die Aufgabe, den Arbeitspunkt eines npn-Transistors unter Zuhilfenahme von Emitterwiderständen, also mit Stromgegenkopplung einzustellen und in einem vorgegebenen Temperaturbereich so festzuhalten, dass die Schwankungen auf Grund von Exemplarstreuungen oder Temperaturschwankungen innerhalb des vorgegebenen Bereichs bleiben. Bild 1: Verstärkerschaltung mit Bipolartransistor R1 und R2 sind die klassischen Widerstände des Basisspannungsteilers. RS ist bei der Bootstrap-Schaltung (zur Erhöhung des Eingangswiderstandes) notwendig. Soll RS nicht zum Einsatz kommen, ist er im Weiteren durch einen Kurzschluss (RS = 0 Ω) zu ersetzen. RE' und RE'' dienen zur Gleichstromgegenkopplung, RE' zur Wechselstromgegenkopplung. RC ist der Kollektorwiderstand, der einerseits die Spannungsverstärkung und den Ausgangswiderstand der Stufe bestimmt, andererseits die Kollektor-Emitterspannung UCE bestimmt. RG ist der Innenwiderstand des Generators (Quelle), die die Spannung UE liefert, RL ist der Lastwiderstand. UB ist die Betriebsspannung und vom Systemdesign festgelegt. Zur Berechnung ihrer Eigenschaften wird die Schaltung in eine Gleichstrom- und in eine Wechselstrom-Ersatzschaltung aufgespalten. Für die Arbeitspunkteinstellung ist die Gleichstrom-Ersatzschaltung von Interesse, die Wechselstromeigenschaften der Schaltung werden in dieser Arbeit nicht behandelt. Alle Kapazitäten werden durch Unterbrechungen ersetzt, alle Induktivitäten werden durch einen Kurzschluss ersetzt. Durch die Spannungsquelle UE und den Generatorwiderstand RG sowie durch den Lastwiderstand RL kann kein Gleichstrom fließen, da die Koppelkondensatoren CK1 und CK2 für Gleichstrom einen unendlich hohen Widerstand darstellen. Auch durch CE kann kein Gleichstrom fließen. Das Ergebnis ist die Gleichstrom-Ersatzschaltung aus Bild 2. Der Spannungsteiler aus R1 und R2 mit der Betriebsspannung UB werden in eine Ersatzspannungsquelle umgerechnet, die Widerstände RE' und RE'' werden zum Widerstand RE zusammengefasst. Die Rechnung ergibt für den Spannungsteiler aus R1 und R2 eine Hilfsspannungsquelle mit der R2 R1∗R2 Leerlaufspannung U H =U B∗ und dem Innenwiderstand R12= , der ParallelR1R 2 R1R 2 schaltung aus R1 und R2. Bild 3: Schaltung mit Hilfsspannungsquelle Bild 2: Gleichstromersatzschaltung Mit diesen Vorbereitungsschritten wird die Ersatzschaltung wesentlich übersichtlicher. R12R S =Ri liefert die BerechnungsDie Substitution grundlage aus Bild 4. Es gilt die Maschengleichung U H =U BE I B∗Ri I E∗R E =U BE I E∗ Bild 4: Berechnungsgrundlage Ri RE B1 . Im Allgemeinen ist der Emitterstrom IE gegeben, der Spannungsabfall UBE an der Basis-Emitterdiode und die Stromverstärkung B können aus den Datenblättern des Transistors abgelesen werden. UH, Ri und RE sind die Größen, die es zu bestimmen gilt. Da nur eine Gleichung für die drei Unbekannten vorhanden ist, kann die Aufgabe nicht eindeutig gelöst werden. Diese Gleichung muss aber auch bei der minimalen und maximalen Arbeitstemperatur erfüllt werden. Bei der minimalen Temperatur Tmin soll der kleinste Emitterstrom IETmin fließen. Der Spannungsabfall an der Basis-Emitterdiode ist dabei UBETmin, Die Stromverstärkung ist BTmin. Bei der maximalen Arbeitstemperatur Tmax fließt der größte Emitterstrom IETmax, es fällt UBETmax an der BasisEmitterdiode ab und die Stromverstärkung ist BTmax. Es lassen sich also zwei Gleichungen für die von der Temperatur unabhängigen Hilfsspannung UH anschreiben und aus welchen UH eliminiert wird und anschließend auf Ri umgestellt wird U H =U BETmin I ETmin∗ Ri Ri R E =U BETmax I ETmax∗ RE B Tmin1 BTmax 1 liefert nach der Umstellung R i= U BETmax−U BETmin I ETmax −I ETmin ∗R E I ETmin I − ETmax BTmin1 BTmax 1 In dieser Gleichung ist RE frei wählbar. Wird RE zu klein gewählt, erhält man für Ri negative Werte. Die Schaltung wäre nicht realisierbar. Es muss RE U BETmin −U BETmax I ETmax −I ETmin gewählt werden. Die maximal erlaubte Schwankung des Spannungsabfalls an R E muss größer sein als die Schwankung der Basis-Emitterspannung am Transistor. Wird RE zu groß gewählt, ist die Kollektor-Emitterspannung möglicherweise zu klein oder RC wird zu klein. Es kann auch sein, dass aus der Berechnung von RC ein negativer Wert resultiert. Es gibt einen sinnvollen Wertebereich für RE zur brauchbaren Realisierung der Arbeitspunkteinstellung. Nun sind RE und Ri festgelegt. Die Hilfsspannung UH entspricht der Leerlaufspannung des Spannungsteilers. Ihr Wert wird aus einer der beiden Maschengleichungen bestimmt. Sie kann nur dann einfach gemessen werden, wenn die Basis des Transistors nicht angeschlossen ist. Da Ri aus der Serienschaltung von R12 und RS besteht, können die Widerstände R1 und R2 aus R1= UB ∗ Ri−R S UH R 2= und UB ∗ Ri− RS . U B−U H Tmin, Tmax, IETmin und IETmax und UB sind vom Design festgelegt. Die Basis-Emitterspannung ist in den Datenblättern nur durch einen Bereich festgelegt, in welchem sich der tatsächliche Wert bewegt. Dieser Wertebereich wird bei der Messtemperatur T0, die in den Daten zu finden ist und typisch 20°C beträgt, angegeben. Die Minimale Spannung bei der Messtemperatur ist U BEmin, die maximale U BE Spannung UBEmax. Die Änderung wird mit bezeichnet und ist typisch -2.2mV/°C bei SiliT ziumhalbleitern. Da die Flussspannung des pn-Übergangs mit steigender Temperatur kleiner wird, gilt bei der maximalen Temperatur Tmax U BETmax =U BEmin U BE ∗ T max −T 0 T und bei der minimalen Temperatur Tmin U BETmin =U BEmax U BE ∗ T min −T 0 . T Die Gleichstromverstärkung B liegt bei der Temperatur T0 zwischen den Werten Bmin und Bmax. Als 1% 1% Daumenregel gilt, dass sie um bzw. steigt. Das bedeutet, dass °C K BTmax =B max∗1.01 T max −T 0 1K und BTmin= Bmin∗1.01 T min −T 0 1K ist. Nun sind alle Kenngrößen vorhanden und die Berechnung kann eindeutig durchgeführt werden. Es ist aber noch immer de Kollektorwiderstand RC unbestimmt. Es gibt einige Möglichkeiten, RC sinnvoll zu bestimmen. Ist die Spannung UCE am Transistor vorgegeben, ist der Widerstand aus RC =2∗ U B −U CE − RE I ETmax I ETmin zu berechnen. Ist UCE nicht vorgegeben, kann RC für maximale Aussteuerung aus RC = bestimmt werden. UB R − E I ETmax I ETmin 2 Beispiel: Der Transistor BFR91A soll im Temperaturbereich von Tmin = -20°C bis Tmax = 70°C bei einem Emitterstrom von IETmin = 5.5mA bis IETmax=6.5mA eingesetzt werden. Die Versorgungsspannung ist mit UB=10V vorgegeben. Der Bootstrap-Widerstand RS wird nicht benötigt. Es handelt sich um einen Silizium-Transistor. Bei diesen gilt U BE 2.2mV 2.2mV . =− =− T °C °K RS wird durch einen Kurzschluss (0Ω) ersetzt. Aus den Datenblättern erhält man bei der Messtemperatur T0=20°C die Werte für UBEmin=0.6V, UBEmax=0.65V und Bmin=40 und Bmax=90. Die Gleichungen für UBE liefern U BETmin =U BEmax U BE ∗ T min −T 0 =0.65V−0.0022V∗−20−20 =0.738V T U BETmax =U BEmin U BE ∗ T max −T 0 =0.60V−0.0022V∗70−20 =0.490V T und aus den Formeln für Stromverstärkung erhält man BTmax =B max∗1.01 BTmin= Bmin∗1.01 RE muss größer als T max −T 0 1K T min −T 0 1K =90∗1.0170−20 =148.0 =40∗1.01−20−20 =26.87 U BETmin −U BETmax 0.738−0.490 = k =248 sein. I ETmax −I ETmin 6.5−5.5 Wählt man RE = 470Ω, wird Ri = U BETmax−U BETmin I ETmax −I ETmin ∗R E 0.490V−0.738V 6.5−5.5 mA∗470 = =1.444k I ETmin I ETmax 5.5mA 6.5mA − − 26.871 1481 BTmin1 BTmax 1 U H =U BETmin I ETmin∗ Ri 1444 R E =0.738V5.5mA∗ 470 =3.608V . B Tmin1 1481 Die Widerstände für den Basisspannungsteiler sind R1= UB 10V ∗ Ri−R S = ∗ 1444−0 =4.00k UH 3.608V mit dem nächstliegenden Normwert aus E12: 3.9kΩ R2= R i−R S ∗ UB 10V = 1444−0 ∗ =2.26k U B−U H 10V−3.608V mit dem nächst liegenden Normwert aus E12: 2.2kΩ. Da UCE nicht vorgegeben ist, wird RC = UB R 10V 470 − E= − =598 I ETmax I ETmin 2 6.5mA5.5mA 2 mit dem nächstgelegenen Normwert aus E12: 560Ω. In der Tabelle 1 ist mit Hilfe eines Tabellenkalkulationsprogramms die Arbeitspunkteinstellung für verschiedene Emitterwiderstände RE durchgeführt worden. Tmin °C -20 Tmax °C 70 UBEmin V 0,600 T0 °C 20 IETmin mA 5,5 IETmax mA 6,5 UB V 10 UCE V UBEmax V 0,650 Bmin / 40 Bmax / 90 dUBE/dT mV/K -2,2 UBETmin V 0,738 UBETmax V 0,490 BTmin / 26,87 BT max / 148,02 RS Ohm 0 RE Ohm 100 120 150 180 220 270 330 390 470 560 680 820 1000 1200 1500 1800 2200 2700 3300 3900 4700 5600 6800 10000 Ri Ohm -963 -833 -637 -442 -182 143 533 924 1444 2029 2810 3720 4891 6192 8143 10094 12696 15948 19850 23752 28956 34809 42614 63426 UH V 1,098 1,234 1,437 1,641 1,912 2,251 2,658 3,065 3,608 4,219 5,033 5,982 7,203 8,560 10,595 12,630 15,344 18,736 22,806 26,876 32,303 38,408 46,549 68,257 R1 Ohm -8766,6 -6748,1 -4434,9 -2695,6 -952,4 635,6 2006,3 3013,0 4001,9 4810,3 5583,0 6218,8 6789,9 7233,3 7685,5 7992,0 8274,2 8511,9 8703,9 8837,7 8963,7 9062,9 9154,7 9292,3 R2 Ohm -1081,3 -949,7 -744,4 -529,1 -225,2 184,7 726,4 1331,8 2258,9 3509,9 5656,2 9259,6 17488,6 43000,6 -136812,7 -38376,3 -23757,9 -18255,9 -15500,7 -14074,6 -12982,8 -12253,1 -11659,4 -10887,4 RC Ohm 783,3 773,3 758,3 743,3 723,3 698,3 668,3 638,3 598,3 553,3 493,3 423,3 333,3 233,3 83,3 -66,7 -266,7 -516,7 -816,7 -1116,7 -1516,7 -1966,7 -2566,7 -4166,7 UCE V 4,70 4,64 4,55 4,46 4,34 4,19 4,01 3,83 3,59 3,32 2,96 2,54 2,00 1,40 0,50 -0,40 -1,60 -3,10 -4,90 -6,70 -9,10 -11,80 -15,40 -25,00 RE'+RE'' Ohm 446 Ri Ohm 1288 UH V 3,445 R1 Ohm 3737,9 R2 Ohm 1964,6 RC Ohm 610,3 UCE V 3,66 Tabelle 1: Berechnung mit Hilfe eines Tabellenkalkulationsprogramms. Die Werte in den doppelt umrahmten Feldern sind vom Anwender einzugeben. Die Zeilen in schwarzer Schrift enthalten die physikalisch realisierbaren Werte, Felder mit roter Schrift enthalten Rechenwerte, welche für die Arbeitspunkteinstellung sinnlos sind.