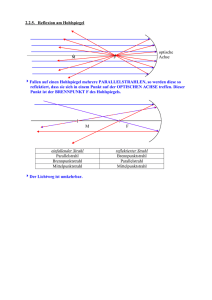
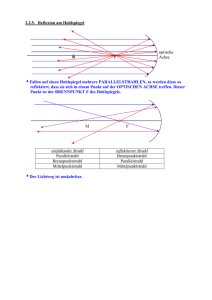
¨Ubungen zu Materialwissenschaften II

Übungen zu Materialwissenschaften II
Prof. Alexander Holleitner
Übungsleiter: Jens Repp / Eric Parzinger
Kontakt: [email protected] / [email protected]
Blatt 2, Besprechung: 23.04.2014 / 30.04.2014
Aufgabe 2.1: Wiederholung: komplexer Brechungsindex
Die komplexe Permittivität ˜ kann durch das Drude- Modell und das Lorenz- Modell
beschrieben werden. Erläutern Sie, ausgehend von den Bewegungsgleichungen, die Unterschiede zwischen den beiden Theorien.
Lösung
Der Brechungsindex n0 ist eine komplexe Funktion mit einem Realteil n und einem Imaginärteil κ:
n0 = n − iκ
Im folgenden soll der komplexe Brechungsindex an der Grenzfläche eines Metalls betrachtet werden. Dazu wird der Wellenvektor k mit Hilfe der Dispersionrelation k = ωc n0 =
ω
(n − iκ) ausgedrückt. Für eine ebene einlaufende Welle gilt:
c
E = E0 exp[i(ωt − kr)]
(n − iκ))]
E = E0 exp[i(ωt − ωr
c
ωr
κ]
E = E0 exp[i(ωt − c n)] exp[− ωr
c
Neben dem Schwingungsterm mit komplexer Exponentialfunktion gibt es zusätzlich noch
einen Term mit reeller, negativer Exponentialfunktion. Die elektromagnetische Welle
nimmt exponentiell ab, wenn sie auf ein Medium mit komplexem Brechungsindex trifft.
Der Imaginärteil κ ist für die Absorption verantwortlich. Der Brechungsindex ist die Wur√
zel der Dielektrischen Funktion n = . Diese soll nun an Hand der Bewegungsgleichung
für ein Elektron hergeleitet werden:
Im Lorenzmodell wird angenommen, dass ein an den Atomkern gebundenes Elektron
von der einfallenden elektromagnetischen Welle zur Schwingung angeregt wird. Die Bewegungsgleichung beschreibt dabei einen getriebenen, harmonischen Oszillator:
2
m ddt2x + mγ dx
+ mω02 x = −eE0 exp (iωt)
dt
Daraus kann die dielektrische Funktion abgeleitet werden (siehe Aufgabe 1.2 auf Übungsblatt
1):
1
(ω) = 1 +
nV e2
1
0 m (ω0 −ω 2 )−iγω
In der nachfolgenden Figur ist jeweils der Realteil und der Imaginärteil der Dielektrischen Funktion gezeichnet:
Lediglich in der unmittelbaren Nähe einer Resonanzfrequenz ω0 (Also der Eigenfrequnz der gebundenen Elektronen) nimmt der Realteil der dielektrischen Funktion negative
Werte und der Imaginärteil von Null verschiedene Werte an. Da der Brechungsindex die
Quadratwurzel der dielektrischen Funktion ist, hat er daher nur in der Nähe einer Resonanzfrequenz einen Imaginärteil, d.h. dort tritt Absorption auf.
Im Drude-Modell werden frei bewegliche, nicht an einen Kern gebundene Elektronen
angenommen, wie sie typischerweise in Metallen vorkommen. In der Bewegungsgleichung
kann daher der lineare Term, der die Rückstellkraft der Atomkerne berücksichtigt, vernachlässigt werden. Die dielektrische Funktion nimmt dann folgende Gestalt an (siehe
Aufgabe 1.2 auf Übungsblatt 1):
(ω) = 1 −
nV e2
1
0 m ω(ω+iγ)
wobei ωp =
q
=1−
ωp2
ω(ω+iγ)
nV e2
0 m
als Plasmafrequenz bezeichnet wird. Unter Vernachlässigung der
q
2
√
Dämpfung (γ = 0) gilt n = = 1 − ωωp . Der Brechungsindex hängt somit von
der Plasmafrequenz ab. Für ω < ωp wird der Brechungsindex rein imaginär, d.h. R → 1,
die Reflektion wird maximal. Für ω > ωp wird der Brechungsindex reel, es findet keine
Absorption mehr statt und die Reflektion nimmt ab. In Metallen sind sowohl gebundene
als auch freie Elektronen vorhanden. Reflektion und Absorption sind durch die Frequenz
der einfallenden elektromagnetischen Welle bestimmt. Für Frequenzen unterhalb der Plasmafrequenz kann die Reflektion durch das Hagen-Rubens-Gesetz angenährt werden (siehe
Aufgabe 1.2 auf Übungsblatt 1). Oberhalb der Plasmafrequenz werden Metalle transparent. Absorption tritt bei bestimmten Resonanzfrequenzen auf. In der nachfolgenden
Abbildung ist ein typisches Reflektionsspektrum für ein Metall gezeigt.
2
Aufgabe 2.2: λ/2 - Platte
Für eine λ/2 - Platte verwendet man einen doppelbrechenden Kristall, der so geschnitten
ist, dass die optische Achse parallel zur Oberfläche und senkrecht zur Ausbreitung des
Lichts liegt. Es soll aus einem Quarzkristall no = 1, 5442, ne = 1, 5533 eine λ/2-Platte
für λ = 530nm hergestellt werden. Der Unterschied des optischen Weges der Platte sei
gegeben als ∆l = d(n0 − ne ) mit Dicke d und den Brechungsindizes n0 und ne .
(a) Wie dick muss der Quarzkristall geschnitten werden, wenn der Gangunterschied zwischen ordentlichem und außerordentlichem Licht λ/2 betragen soll?
(b) Wie dick muss ein Kalkspatkristall (no = 1, 658, ne = 1, 486 ) geschnitten werden, um
daraus eine λ/2-Platte herzustellen? Warum werden in der Praxis λ/2-Platten nicht
aus Kalkspat hergestellt?
(c) Bei welchem Winkel zwischen optischer Achse und Polarisationsrichtung des einfallenden Lichts wird die Polarisationsrichtung um 90◦ gedreht?
(d) Wie kann die Drehung der Polarisationsrichtung um willkürliche Winkel (6= 90◦ ) erreicht werden?
Lösung
Doppelbrechende Materialien haben die Eigenschaft, ein Lichtbündel in zwei senkrecht zueinander polarisierte Teilbündel zu trennen. Fällt unpolarisiertes Licht senkrecht auf ein
doppelbrechendes Material, so gibt es neben dem ordentlichen Strahl, der entsprechend
des Snelliusschen Brechungsgesetz nicht gebrochen wird, noch einen außerordentlichen
Strahl, der auch bei senkrechtem Einfall an der Grenzfläche gebrochen wird. Doppelbrechende Materialien besitzen für unterschiedliche Polarisation und Richtung der einfallenden elektromagnetischen Welle einen unterschiedlichen Brechungsindex. Es gibt daher
3
zwei unterschiedliche Ausbreitungsgeschwindigkeiten: eine zur optischen Achse senkrechte
Ausbreitungsgeschwindigkeit v⊥ und eine zur optischen Achse parallele vk .
Die Polarisationsebene ist nun ausschlaggebend, ob der Strahl gebrochen wird oder nicht.
Die Bei Licht, das parallel zur Zeichenebene polarisiert ist (Figur oben rechts), bilden
die Elementarwellen entsprechend des Huygensschen Prinzips aufgrund der unterschiedlichen Ausbreitungsgeschwindigkeiten Rotationsellipsoide. Die resultierende Wellenfront
wird gegenüber der einfallenden Wellenfront gebrochen. Ist das licht senkrecht zur Zeichenebene polarisiert gibt es keine unterschiedlichen Brechungsindizes, die Elementarwellen sind Kugelwellen, der Strahl wird nicht gebrochen und gehorcht dem Snelliusschen
Brechungsgesetz. Die Brechungsindizes können aus den Ausbreitungsgeschwindigkeiten
berechnet werden:
nao = vck
no = vc⊥
Doppelbrechende Materialien werden für Verzögerungsplatten verwendet. Hier sind die
Kristalle so geschnitten, dass die optische Achse parallel zur Oberfläche und senkrecht
zur Ausbreitung des Lichts liegt. Außerordentlicher und ordentlicher Strahl werden in
diesem Fall nicht gebrochen. Die unterschiedlichen Brechungsindizes führen jedoch zu unterschiedlichen Ausbreitungsgeschwindigkeiten entsprechend ihrer Polarisationsebene. Die
Schwingungsebene, in der die Ausbreitungsgeschwindigkeit am größten ist, wird schnelle
Achse, die Ebene senkrecht dazu als langsame Achse bezeichnet. Parallel zur schnellen
Achse polarisiertes Licht durchläuft den Kristall schneller als Licht, das senkrecht dazu
polarisiert ist.
4
Einfallendes Licht kann nun entsprechend der obigen Zeichnung in zwei linear polarisierte
Komponenten parallel und senkrecht zur optischen Achse aufgeteilt werden. Nach dem
beide Wellen die Verzögerungplatte durchlaufen haben, weisen sie eine Phasenverschiebung zueinander auf:
∆l = d · (nlangsam − nschnell )
∆ϕ = 2π
· d · (nlangsam − nschnell ) Die beiden Wellen überlagern sich hinter dem Kristall
λ
(Interferenz) zum ausgehenden Licht. Durch die (kohärente) Überlagerung dieser beiden
Wellen ergibt sich eine neue Polarisation des Lichtes
(a) Damit der optische Wegunterschied zwischen ordentlichem und außerordentlichen
Strahlt genau λ/2 beträgt muss gelten:
∆l = d(n0 − ne ) =
→d=
λ
2
λ
/(n0 − ne ) = 530nm/(1, 5533 − 1, 5442) = 2, 912 · 10−5 m
2
(b) Für die Dicke eines Kalkspatkristalls gilt analog
λ
d = | /(n0 − ne )| = |530nm/(1, 486 − 1, 657)| = 1, 54068 · 10−6 m
2
Durch den großen Unterschied der Brechungsindizes von ordentlichem und außerordentlichen Strahl ergeben sich sehr kleine Schichtdicken, die technisch sehr aufwendig
herzustellen sind. Daher werden bevorzugt Materialien verwendet, deren Brechungsindizes sich nur geringfügig unterscheiden.
(c) Entsprechend der Figur oben kann Licht, das unter einem Winkel α zur optischen
Achse polarisiert ist, in Komponenten senkrecht und parallel zur optischen Achse aufgespalten werden. Nach dem der Lichtstrahl die λ/2-Platte durchlaufen hat, ist der
5
ordentliche Strahl gegenüber dem außerordentlichen Strahl um λ/2 verzögert, was
einem Phasenunterschied von π entspricht. Dadurch ändert sich für eine Komponente
des elektrischen feldes, z.B. E⊥ das Vorzeichen. Dadurch ändert sich die Polarisationsrichtung des auslaufenden E-Feldes gegenüber des einlaufenden Feldes um 2α.
Um eine Drehung der Polarisationsrichtung von 90◦ zu erreichen muss der Winkel
zwischen Polarisationsrichtung und einfallender Achse α = 90◦ /2 = 45◦ betragen.
(d) wie oben beschrieben wird die Polarisationsrichtung des ausfallenden Lichts gegenüber
der Polarisationsrichtung des einfallende Licht um 2α gedreht. Durch geeignete Wahl
von α ist somit jede beliebige Polarisationsrichtung möglich.
6