Vorlesung 22

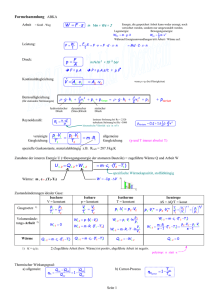
Heißluftmotor als Kältemaschine
Oberem Raum wird Wärme entzogen!
Kühlwasser
Arbeitsgas oben
a-b:Expansion: Arbeitsgas
entzieht der Umgebung Wärme
b-c: Verdrängerkolben hoch T2
Kupferwolle wird Wärme entzogen
c-d: Kompression àWärme geht ins Kühlwasser
d-a: Verdrängerkolben nach unten T1
Kupferwolle nimmt Wärme auf,Gas kühlt ab
Der Heißluftmotor als Wärmepumpe
Unterem Raum wird Wärme entzogen und oben zugefügt
Arbeitsgas unten:
a-b: Expansion: Wärme aus
dem Kühlwasser
b-c: Verdrängerkolben nach unten
T2 Kupferwolle wird Wärme entzogen
c-d: Kompression àWärme an oberen Zylinderraum
Wärme an oberen Zylinderraum
5.8.Thermodynamische Arbeit
Gas (P,V,T),(P,V,T) sind die Zustandsgrößen
1,2,3,4 sind Gleichgewichtszustände
Wir betrachten quasistatischen Prozess:
Änderung von P,T,V ''sehr
langsam, sehr klein''
Prozess ist reversibel!
z.B: Sand: + Sandkörnchen
Kolben runter
- Sandkörnchen
Kolben zurück
Irreversible Prozesse:
z.B: Chemische Reaktionen, Parfüm à
Luft
Die vom System geleistete Arbeit
5.9.Der Carnot -Zyklus
(Der effizienteste Wärmezyklus)
Wärmeaustausch möglich oder unterbrochen!
1,3: Isotherm
2,4: Adiabatisch
Prozesse reversibel!
1:
positiv,
2:
positiv,
3:
4:
für die adiabatischen
Prozesse gilt:
Insgesamt:
Wirkungsgrad der CARNOT- Maschine
mit
=
Volumen nach Durchlaufen von 1 etc.)
analog:
Resultat: Nur ein Teil von
kann in Arbeit umgewandelt
werden!
Es ist unmöglich einen thermodynamischen Prozess
zu durchlaufen, dessen einziges Resultat es ist, Wärme
aus einem Resevoir ganz in Arbeit umzuwandeln!
Kelvin(1824-1907)
5.10. Zweiter Hauptsatz der Thermodynamik
R. Claudius (1822-1888) ab 1865 in Bonn:
Nicht alle energieerhaltenden Prozesse sind möglich
Wärme, wenn keine Arbeit geleistet wird, fließt immer
von hoher zu niedriger Temperatur!
Clausius führte den Begriff der Entropie S ein.
mit
oder
Reversibel!
da (s.o):
Irreversible Prozesse haben
Clausius: 1. Die Energie der Welt ist konstant
2. Die Entropie der Welt strebt einem Maximum zu!''
5.11. Entropie und Wahrscheinlichkeit (Boltzmann)
N=
Beispiel:
N Teilchen in I und II
Wahrscheinlichkeit
II
in I und
z.B.: N=8
Eine Möglichkeit 8 in I
8 Möglichkeiten 1 in I, 7 in II
Bei Gleichverteilung:
d.h: 4 in I 4 in II
je größer P, desto kleiner
P maximal:
Bei
sind alle anderen Zustände höchst
unwahrscheinlich!
Realisierungsmöglichkeiten P
allgemein:
Boltzmann: Irreversibles Wachstum von S entspricht
wachsender molekularer Unordnung!
Zusammenhang zwischen P und S
S= k* lnP
im obigen Beispiel, ist der Endpunkt einer
irreversiblen Entwicklung!
Entropie wächst in Richtung Zukunft, nicht Vergangenheit
Pfeil für die Zeit!
5.12. Dritter Hauptsatz der Thermodynamik
Der thermodynamische Gleichgewichtszustand am
absoluten Nullpunkt ist ein Zustand maximaler Ordnung,
der nur eine Realisierungsmöglichkeit P=1 hat!