5. Akustische Wellen Die Geschwindigkeit akustischer Wellen ist in

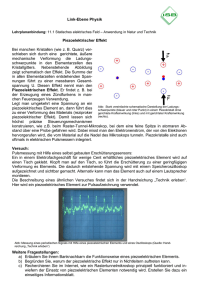
Werkstoffe und Sensorik
37
________________________________________________________________________________________________________________________
5. Akustische Wellen
Die Geschwindigkeit akustischer Wellen ist in hohem
Maße von der Dichte des Mediums und damit der Anwesenheit chemischer Teilchen abhängig. Um neben der
universellen Dichte Informationen über spezifische chemische Teilchen zu erhalten, wird ein selektives Adsorbent benötigt und die Möglichkeit, die Stoffe räumlich zu
konzentrieren, wo sich die akustischen Wellen fortbewegen.
Die hohe Empfindlichkeit kann dazu dienen, physika-
Abb. 5.1.
lische, chemische und biologische Größen zu messen. In
vielen Fällen ist das Ausgangssignal eine Frequenz, die
einfach und präzise messbar ist.
Die ersten Ultraschall-Dampf- und Gas-Sensoren verwendeten schwingende piezoelektrische Kristallplatten,
die frequenzmessende Elemente elektronischer Oszillatoren waren. Darauf wurden spezifische Schichten aufgetragen, um den Dampf oder das Gas zu adsorbieren.
Die Resonanzfrequenz hängt von der Zahl und der Art
der Moleküle ab.
In neuerer Zeit werden besonders die Vorzüge anderer
38
Werkstoffe und Sensorik
________________________________________________________________________________________________________________________
Sensorkonfigurationen genutzt, z. B. die Bewegung der
Ultraschallwelle entlang der Oberfläche eines Festkörpers
oder in einer sehr dünnen Membran oder Platte (s. Abbildung 5.1.).
Bewegung elastischer Wellen
Unbegrenzter Festkörper: Nur Longitudinal- und Transversalwellen (analog zu Druckwellen). Die Bewegung
der Atome wird als klein gegenüber wenigen Ångström
Abstand zwischen den Atomen angenommen. Es gilt
dann das Hookesche Gesetz mit einem linearen Zusammenhang zwischen Wellendruck und -verschiebung.
Tij = C ijkl S kl
(5.1)
Tij: Druck entlang der i-Koordinate auf einer Oberfläche
mit der Normalen senkrecht zur xj-Achse, Skl: Verschiebung, definiert durch:
S kl =
1
2
È∂u k
∂ui ˘
Í ∂x + ∂x ˙
Î 1
k ˚
(5.2)
u: Verschiebung in Richtung k, cijkl: elastische Steifigkeitskonstante.
Mit der Newton´schen Kraftgleichung
Fi =
∂Tij
∂2u
= p 2k
∂x j
∂t
(5.3)
läßt sich die elastische Wellengleichung für homogene
elastische Festkörper ableiten
p
∂ 2 ui
∂2 u k
=
c
ijkl
∂t2
∂x i ∂x j
(5.4)
r: Dichte des Mediums. Lösungen sind der Realteil von
[
]
u = A exp ik (l i ri - vt)
(5.5)
Die Lösung liefert die Phasengeschwindigkeit v der Volumenwellen.
Eine Oberflächenwelle (SAW) breitet sich entlang der
Oberfläche eines semi-infiniten Festkörpers aus. Die
Geschwindigkeit ist unabhängig von der Frequenz (wie
für Volumenwellen). Die Teilchenbewegung einer SAW
ist nahe der Oberfläche am größten und nimmt innerhalb
1 Å praktisch auf 0 ab. Die Kräfte auf der Seite der freien
Oberfläche verschwinden.
Die SAW-Geschwindigkeit ist in jedem Festkörper
geringfügig geringer als die der TransversalVolumenwelle. Liegt der Ausbreitungsvektor xk in der Ebene
einer Kristallsymmetrie, so bewegen sich die Teilchen an
der Oberfläche entlang elliptischer Pfade in der Ebene
senkrecht zur Oberfläche (wie Wellen auf Wasseroberflächen).
Abb. 5.2.
Bei einer Platte verschwinden die Kräfte an beiden Oberflächen. Die Lösungen heißen Lambwellen, deren Geschwindigkeit vom Plattenmaterial und dem Verhältnis
Plattendicke/Wellenlänge abhängt. Diese Platten-Moden
können in symmetrische und unsymmetrische eingeteilt
werden, abhängig von der Symmetrie der Bewegungs-
Werkstoffe und Sensorik
39
________________________________________________________________________________________________________________________
- Orientierung des angewandten elektrischen Feldes
relativ zur kristallographischen Achse
- relative Anordnung der kammähnlichen Elektroden und
des Substrats, wenn ein piezoelektrischer Film auf einem nicht piezoelektrischen Substrat verwendet wird
- Verhältnis räumlich periodischer Abstands / Wellenlänge für SAW und Platten-Moden.
Für einen piezoelektrischen Festkörper wird das einfache
Hookesche Gesetz durch die piezoelektrischen Zustandsgleichungen ersetzt.
Tij = cijkl Skl - eijm Em
Dn = enkl Skl - enm Em
Abb. 5.3.
Typische SAW-Teilchen-Verschiebung (hor. + ver.) für Wellen,
(5.6)
(eijm: Elemente des piezoeletrischen Tensors des Materials, Em: elektrisches Feld, Dn: elektrische Verschiebung,
enm: dielektrische Permittivität).
die sich horizontal in einem isotropen Medium ausbreiten.
komponente senkrecht zur Plattenoberfläche (s. Abbildung). Die Geschwindigkeit ist stark von der Plattendicke
abhängig. Die höchste Enpfindlichkeit für den Nachweis
von Gasen wird für die antisymmetrische Mode der geringsten Ordnung erreicht für eine sehr dünne Platte.
Eine bequeme Ankopplung elektrischer Stromkreise an
elastische Wellen stellen piezoelektrische Effekte dar.
Die frühesten Volumenwellen-Sensoren waren Platten
aus kristallinem Quarz SiO2. Für Oberflächenwellen ist
die Auswahl größer: Kristallines Quarz, Ferroelektrische
Einkristalle von LiNbO3, dünne Filme aus ZnO.
Die Größe des piezoelektrischen Effekts hängt von
den verwendeten Elektroden ab. Um eine Volumenmode
elektrisch anzuregen, wird eine Wechselspannung zwischen großflächigen Elektroden an den beiden gegenüberliegenden Flächen einer Kristallplatte angelegt. Die
piezoelektrischen Drücke werden an der Grenzfläche
Platte/leitende Elektroden erzeugt, die bei der Betriebsfrequenz üblichen Weise eine halbe Wellenlänge entfernt
sind. Daher addieren sich die Wellen, die an jeder Elektrode erzeugt werden, in Phase während sie die Dicke des
Teils durchqueren. Es bauen sich resonante Schwingungen auf.
Für SAW und Platte-Moden sind die übertragenden
Elektroden entweder interdigital oder unipolar kammähnlich, mit Abständen gleich der Wellenlänge oder
ganzzähligen Vielfachen davon.
Die Stärke der Kopplung eines gegebenen piezoelektrischen Materials hängt von mehreren Faktoren ab:
- piezoelektrische und elastische Eigenschaften des Materials selbst
Eine Welle eines elektrischen Feldes begleitet jetzt die
elastische Welle. Die Wellengeschwindigkeit hängt von
den elastischen, piezoelektrischen und dielektrischen
Eigenschaften ab. Das Medium verhält sich "steifer"
durch die zusätzliche potentielle Energie, die von der
piezoelektrischen Kopplung herrührt. Die Geschwindigkeiten sind höher als ohne Kopplung ("piezoelektrische
Versteifung"). Elastische Versteifung
cversteift = c (1 + K2)
K2 = e2/ce
∆ (eijmEm)
(5.7)
K 2 = e2 / c e
=elektromechanischer Kopplungskoeffi-
zient. Durch Anwendung des Newtonschen Kraftgesetzes
läßt sich zeigen, daß die Kraft die Form — (eijmEm) hat.
D. h., die Schallwellen in piezoelektrischen Materialien
sind die Gebiete, wo lokale Änderungen piezoelektrischer
Kopplungskoeffizienten e oder des elektrischen Feldes
auftreten. Im Volumen treten beide Änderungen dort auf,
wo die leitfähigen Elektroden den Kristall kontaktieren.
In SAW und Plattenmoden sind die stärksten Quellen
dort, wo die Elektroden den Kristall berühren oder an den
Elektrodenkanten, wo das elektrische Feld am stärksten
konzentriert ist.
Es wird beobachtet, daß folgende Beziehung für die
Phasengeschwindigkeit der elastischen Welle besteht:
u=
Steifheit/Dichte
(5.8)
Piezoelektrische Kopplung erhöht die Geschwindigkeit.
Temperaturerhöhung erniedrigt die Geschwindigkeit.
40
Werkstoffe und Sensorik
________________________________________________________________________________________________________________________
Tab. 5.1. Factors that affect ultrasonic wave velocity. B, S, and P denote bulk, surface and
flexural plate modes respectively
Ebenso erniedrigen Erniedrigungen der Dichte die Phasengeschwindigkeit. Die Tabelle 5.1. zeigt einige Größen,
die die Geschwindigkeit beeinflussen.
Volumensensoren: Änderungen durch Adsorption von
Gasmolekülen nur an der Oberfläche.
∆u/ures = Sm∆m
(5.9)
Bequemste Methode der Verknüpfung elektrischer Stromkreise mit elastischen Wellen:
Piezoelektrischer Effekt (elektrische Polarisationsladungen
¤ mechan. Druck)
Piezoelektrizität zeigen
Materialien mit asymmetrischer ionischer Polarisation
als Ergebnis der Wechselwirkung zwischen CoulombKräften und elastischen Kräften.
Beispiele:
Natürlicher Quarz, LiNbO3
(ferroelektrisch), PZT (Sinterkörper), CdS, ZnO (Dünnschichten), Polymere (Poly (Vinyl-Fluorid)).
Für Sensor-Anwendungen erforderlich:
- Hoher piezoelektrischer Kopplungs-Wirkungsgrad
- Gute Temperatur-Stabilität
- Geringe Ausbreitungsverluste
- Chemische Stabilität
Sm: Proportionalitätsfaktor. Beispiel: Die Frequenz eines
6-MHz AT-geschnittenen Quarzkristallresonators nimmt
um ein Hz ab, wenn 12 ng-Gasmoleküle/cm2 auf eine der
Flächen adsorbiert sind.
Selektivität
Neben einem "aktiven Sensor" wird ein "Referenzsensor"
verwendet, der der gleichen Umgebungstemperatur und
dem gleichen Druck unterworfen ist, während das aktive
Element alleine auf die Meßgröße reagiert. Beispiele: s.
Tabelle 5.2.
Akustische Wellen-Sensoren bestehen aus den beiden
Elementen:
- Akustische Sonde
- Selektive Beschichtung
Abb. 5.4.
Diese Kriterien werden von vielen Materialien erfüllt
(besonders SiO2, LiNbO3, ZnO auf SiO2).
Unterschiedliche Massenempfindlichkeiten: Sie ist für
YX-Quarz 1.8 x höher als für ZX-ZnO und 2.5 x höher
als für YZ-LiNbO3.
Wahl des piezoelektrischen Materials und der Orientierung abhängig von der gewünschten Ausbreitung der
Welle:
- AT- und BT-geschnittener Quarz vibriert parallel zu
den Ebenen, die eine Scherung zeigen. fi Bulk-modesensors . (Ebenfalls: keine Temperaturabhängigkeit)
- ST-geschnittener Quarz: Æ SAW (Ebenfalls: keine
Temperaturabhängigkeit)
LiNbO3 hat wesentlich höhere piezoelektrische Kopplung als Quarz, aber eine relativ hohe Temperaturabhängigkeit der Geschwindigkeit. Gesputtertes ZnO hat
eine mittlere Kopplung, und es ist möglich, (für einen
engen Wellenlängenbereich) die Temperaturabhängigkeit
von LiNbO3 zu kompensieren.
Werkstoffe und Sensorik
41
________________________________________________________________________________________________________________________
Tab. 5.2. Possible approaches for obtaining selective gravimetric response
n: Zahl der Moleküle/Zeitund Flächeneinheit, t :
mittlere Zeit der Haftung
eines Moleküls an der Oberfläche,
t hat eine exponentielle
Abhängigkeit von der
Sorptionsenergie.
ii) Lösungs-Konzept:
Für flüssige oder amorphe
Festkörper oberhalb der
Erweichungstemperatur
(z.B. elastomere Polymere)
kann die Löslichkeit des
Gases herangezogen werden. Frequenzverschiebung
für SAW-Sensor:
∆ƒn = ∆ƒsCnK/r
(5.10)
∆ƒn: Frequenzverschiebung
durch Beschichtung, Cn : GasKonzentration, K: Verteilungskoeffizient, r: Beschichtungsdichte.
Verteilungskoeffizienten können der Gas-ChromatographieLiteratur entnommen werden.
Der Verteilungskoeffizient ist
stark temperaturabhängig.
Selektive Beschichtung:
Kritischer Aspekt ist die Stabilität. Oft werden organische
Polymere verwendet, die in Luft oxidieren können. Die
Sensitivität wird durch die Fähigkeit zu sorbieren kontrolliert. Irreversible Wechselwirkungen sind zu vermeiden (außer für Dosimeter). Poröse Materialien mit großer
Oberfläche zeigen schnellere Ansprechzeiten. Die gleichen Beschichtungen sind für alle Moden anwendbar.
Die Energie der Sorption reicht von schwachen vander-Waals Bindungen (< 0.1 kcal/mol) bis zu kovalenten
Bindungen (> 100 kcal/mol). Mittlere Wechselwirkungsenergien sind bevorzugt, z. B. Wasserstoffbindung, Charge-Transfer-Komplexbildung.
Zwei Konzepte für das Design selektiver Beschichtungen:
i) Dynamisches Adsorptions-Konzept.
Langmuir: Kinetische Theorie der Gasadsorption,
Zahl der Moleküle pro Flächeneinheit:
s = nt
Abb. 5.5.