Grundlagen der Programmierung 2 Typen und Typcheck

Grundlagen der Programmierung 2
Typen und Typcheck
Prof. Dr. Manfred Schmidt-Schauÿ
Künstliche Intelligenz und Softwaretechnologie
15. Mai 2007
Haskell, Typen, und Typberechnung
ZIELE dieses Kapitels
Haskells Typisierung
Milners Polymorpher Typcheck
Grundlagen der Programmierung 2
- 1 -
Typisierung in Haskell
Haskell hat eine starke, statische Typisierung.
•
jeder Ausdruck muss einen Typ haben
•
Der Typchecker berechnet Typen
und prüft Typen zur Compilezeit
•
die Theorie sagt:
Es gibt keine Typfehler zur Laufzeit
d.h. kein dynamischer Typcheck nötig.
Grundlagen der Programmierung 2
- 2 -
Typisierung:
sprachen)
Begriffe
(andere
Programmier-
Monomorphe
Typisierung
Alle Objekte, Funktionen haben einen
eindeutigen Typ
Typvariablen gibt es nicht
Konsequenz: verschiedene Längenfunktionen für Listen von unterschiedlichem Typ
Polymorphe
Typisierung
Funktion arbeitet auf mehreren Daten-Typen
Typvariablen: Mittel zur Schematisierung.
parametrischer Polymorphismus.
Eine einzige Längenfunktion für alle Listen reicht aus
Ist auch in Java 5 für generische Typen anwendbar
Grundlagen der Programmierung 2
- 3 -
Bemerkungen zu anderen Programmiersprachen
Verwendung der arithmetischen Operatoren
Überladung von +, ∗, . . .
Manche Programmiersprachen nutzen automatische (dynamische)
Typkonversion
Haskell:
keine Typkonversion
eingegebene Zahlkonstanten sind überladen
eine eingegebene 8 wird vom Compiler
(fromInteger 8) eingefügt
als
Typkonversion von Hand einfügen:
Z.B. pi + 2%3 ergibt einen Typfehler,
pi + (fromRational (2%3)) ergibt 3.80825932::Double
Grundlagen der Programmierung 2
- 4 -
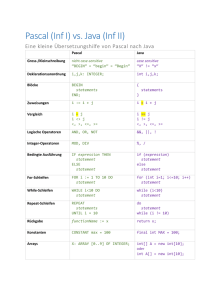
Java und Typisierung
Java 1.4 ist streng getypt. Das Typsystem ist monomorph.
die Java-Klassen entsprechen den elementaren Typen.
Zusätzlich gibt es einen Untertyp-Begriff für Klassen.
Die dynamischen Typfehler sind meist (cast)-Fehler.
Java 5 ist streng getypt. Das Typsystem ist polymorph.
Zusätzlich gibt es einen Untertyp-Begriff für Klassen.
Kompliziertere statische Typangaben nötig
Weniger dynamische Typfehler.
Grundlagen der Programmierung 2
- 5 -
Typisierung, Begriffe
polymorph:
Ein Ausdruck kann viele Typen haben (vielgestaltig,
polymorph).
Die (teilweise unendliche) Menge der Typen entspricht
einem schematischen Typausdruck
[a]->Int ist das Schema
Instanzen sind z.B.
[Int]->Int, [Char]->Int,
Grundlagen der Programmierung 2
[[Char]]->Int
- 6 -
Syntax von Typen in Haskell (ohne Typklassen)
hTypi
::= hBasistypi | (hTypi) | hTypvariablei
| hTypkonstruktorni{hTypi}n
(n = Stelligkeit)
hBasistypi ::= Int | Integer | Float | Rational | Char
Grundlagen der Programmierung 2
- 7 -
Syntax von Typen
Typkonstruktoren können benutzerdefiniert sein (z.B. Baum a)
Vordefinierte
Liste
Typkonstruktoren: Tupel
Funktionen
[·]
(.,...,.)
· → · (Stelligkeit 2, Infix)
Konvention zu Funktionstypen mit →
a→b→c→d
bedeutet:
Grundlagen der Programmierung 2
a → (b → (c → d)).
- 8 -
Bemerkungen und Wiederholung
spezielle syntaktische Konventionen für Tupel und Listen.
Beispiel:
(Int, Char)
[Int]
Typangabe
•
•
•
t :: τ
Basistypen nennt man elementare Typen
Grundtyp: Typ ohne Typvariablen (auch monomorph)
polymorph wenn der Typ Typvariablen enthält.
Grundlagen der Programmierung 2
- 9 -
Beispiele
[1,2,3]
::
[Int]
map
::
(a → b) → [a] → [b]
(:)
::
a → [a] → [a]
length
::
[a] → Int
Grundlagen der Programmierung 2
- 10 -
Interpretation der Typen
length :: [a] → Int
∀a.length :: [a] → Int
logische Formel:
Interpretation:
Für alle Typen a ist length eine Funktion, die vom
Typ [a] → Int ist.
Logisch gilt dann:
∀x.x :: [a] ⇒ (length x) :: Int
Grundlagen der Programmierung 2
- 11 -
Typregeln
Wie berechnet man Typen von Ausdrücken?
Anwendung von Funktionen auf Argumente (σ, τ sind Typen)
s :: σ → τ , t :: σ
(s t) :: τ
Beispiele:
quadrat :: Int → Int , 2 : Int
(quadrat 2) :: Int
+ :: Int → (Int → Int) , 1 :: Int
(1 +) :: (Int → Int)
((1 +) 2) :: Int
Grundlagen der Programmierung 2
, 2 :: Int
- 12 -
Typregel Anwendung: mehrere Argumente
s :: σ1 → σ2 . . . → σn → τ , t1 :: σ1 , . . . , tn :: σn
(s t1 . . . tn) :: τ
Beispiele
+ :: Int → Int → Int, 1 :: Int , 2 :: Int
(+ 1 2) :: Int
+ :: Int → Int → Int
(1 + 2) :: Int
Grundlagen der Programmierung 2
- 13 -
Erweiterung der Anwendungsregel
auf polymorphe Typen
Ziel: Anwendung der Typregel für z.B. length oder map
Die Funktion γ ist eine Typsubstitution
wenn sie Typen für Typvariablen einsetzt
γ(τ ) nennt man Instanz von τ
Beispiel
Typsubstitution:
Instanz:
Grundlagen der Programmierung 2
γ = {a 7→ Char, b 7→ Float}
γ([a] → Int) = [Char] → Int
- 14 -
Erweiterung der Anwendungsregel
auf polymorphe Typen
s : σ → τ,
t : ρ und γ(σ) = γ(ρ)
(s t) :: γ(τ )
Hierbei ist zu beachten:
die Typvariablen in ρ müssen vorher umbenannt werden.
Grundlagen der Programmierung 2
- 15 -
Beispiel zur polymorphen Anwendungsregel
Typ von (map quadrat) ?
map :: (a → b) → [a] → [b]
Instanziiere mit:
ergibt:
{a 7→ Int, b 7→ Int}
map :: (Int → Int) → [Int] → [Int]
Regelanwendung ergibt:
map : (Int → Int) → [Int] → [Int], quadrat :: (Int → Int)
(map quadrat) :: [Int] → [Int]
Grundlagen der Programmierung 2
- 16 -
Polymorphe Anwendungsregel für n Argumente
s :: σ1 → σ2 . . . → σn → τ,
(s
t1 : ρ1, . . . , tn : ρn und ∀i : γ(σi) = γ(ρi)
t1 . . . tn) :: γ(τ )
Die Typvariablen in ρ1, . . . , ρn müssen vorher umbenannt werden.
Beachte verwende möglichst allgemeines γ
Grundlagen der Programmierung 2
- 17 -
Beispiel mit Typvariablen
id x = x
id :: a → a.
Berechne Typ von (map id)
map::
id::
(a → b)
a0 → a0
→ [a] → [b]
Regelanwendung:
map : (a → b) → ([a] → [b]), id :: a0 → a0
(map id) :: γ([a] → [b])
d.h. (map id) :: ([a] → [a]).
Grundlagen der Programmierung 2
- 18 -
Beispiele zu polymorpher Typberechnung
Berechne Typ der Liste [1]:
1. [1] = 1 : []
2. 1 :: Int und [] :: [b]
(Typen der Konstanten)
3. (:) :: a → [a] → [a]
4. Anwendungsregel mit γ = {a 7→ Int} ergibt:
(1 :) :: [Int] → [Int]
5. Anwendungsregel mit γ2 = {b 7→ Int} ergibt:
(1 : []) :: [Int]
Grundlagen der Programmierung 2
- 19 -
Beispiel zu Typfehler
[1, ’a’] hat keinen Typ:
•
•
•
1 : ( ’a’ : [])
(voll geklammert)
1 :: Integer, [] :: [b], ’a’ :: Char
Typen der Konstanten.
(1 :) :: [Integer] → [Integer] und
’a’:[] :: [Char].
Kein Typ als Resultat, denn:
[Integer] und [Char] sind verschieden unter allen γ.
Grundlagen der Programmierung 2
- 20 -
Beispiel zu Typfehler im Interpreter
> [1,’a’]
ERROR - Illegal Haskell 98 class constraint in inferred type
*** Expression : [1,’a’]
*** Type
: Num Char => [Char]
Im aktuellen Interpreter:
No instance for (Num Char)
arising from the literal ‘1’ at <interactive>:1:1
Possible fix: add an instance declaration for (Num Char)
In the expression: 1
Grundlagen der Programmierung 2
- 21 -
Typ eines Ausdrucks
Typ von (map quadrat [1,2,3,4]) :
•
map::
(a → b) → [a] → [b]
•
quadrat::
Integer → Integer, und [1, 2, 3, 4] :: [Integer].
•
γ=
{a 7→ Integer, b 7→ Integer}.
•
Das ergibt:
γ(a) = Integer, γ([a]) = [Integer], γ([b]) = [Integer].
•
Resultat:
γ([b]) = [Integer]
Grundlagen der Programmierung 2
- 22 -
Typisierung von Funktionen und Ausdrücken
Problematik:
rekursiv definierte Funktionen
Lambda-Ausdrücke, let-Ausdrücke
Listen-Komprehensionen.
Typcheckalgorithmus von Robin Milner (in Haskell und ML)
•
•
ist schnell,
liefert allgemeinste (Milner-)Typen
•
schlechte worst-case Komplexität:
in seltenen Fällen exponentieller Platzbedarf
Liefert in seltenen Fällen nicht die allgemeinsten möglichen polymorphen Typen
•
Grundlagen der Programmierung 2
- 23 -
Typisierung von Funktionen, Milner
Satz zur Milner-Typisierung in Haskell:
Sei t ein getypter Haskell-Ausdruck, ohne freie Variablen.
Dann wird die Auswertung des Ausdrucks t
nicht mit einem Typfehler abbrechen.
Allgemeine Aussage zu starken Typsystemen
Keine dynamischen Typfehler, wenn das Programm korrekt getypt ist
Grundlagen der Programmierung 2
- 24 -
Typisierung und Reduktion: Zusammenhang
Erinnerung Beta-Reduktion: ((λx.t) s) −→ t[s/x]
λx.t :: τ1 → τ2 , s :: σ , γ(τ1) = γ(σ)
((λx.t) s) : γ(τ2)
Zum Ermitteln von γ(τ2)
benötigt man eine Typsubstitution γ,
so dass γ(τ1) = γ(σ) ist.
Grundlagen der Programmierung 2
- 25 -
Typisierung und Reduktion: Zusammenhang
((λx.t) s) −→ t[s/x]
Was ist der Typ von t[s/x]?
Beh:
((λx.t) s) :: τ impliziert t[s/x] :: τ
Argumentation:
Folgerung:
Milner-Typcheck beachtet nur den Typ der Unterterme,
nicht deren syntaktische Form.
Typ von x und s ist aber gleich (als Unterterm von t)
denn γ(τ1) = γ(σ)
auch mehrere Beta-Reduktionen erhalten den ursprünglichen Typ
Analoge Argumentation für andere Auswertungsregeln!
Grundlagen der Programmierung 2
- 26 -
Typisierung und Reduktion
Beachte:
Nach Reduktionen kann ein Ausdruck
mehr Typen haben also vorher
Beispiel:
if 1 > 0 then [] else [1]
:: [Integer]
arithmetische-Reduktion:
−→ if True then [] else [1]
:: [Integer]
Case-Reduktion:
−→ []
:: [a]
Grundlagen der Programmierung 2
- 27 -