Statik und Dynamik

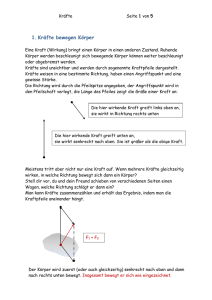
IP
Fakultät Grundlagen
Ingenieurpädagogik
Summer-School
Experimentierfeld 1
Statik und Dynamik
1. Einführung
Überlegungen im Bereich der Statik und Dynamik beruhen stets auf der physikalischen Größe Kraft F. Betrachten wir Kräfte und ihre Wirkung auf einen ausgedehnten Körper, also keinen Massenpunkt, so ist neben der Wirkungsrichtung und dem
Betrag der Kraft auch der Angriffspunkt entscheidend. Die Kraft ist also ein Vektor,
welcher durch Betrag und Richtung definiert ist. Vektorgrößen werden stets durch
r
einen Pfeil über dem Formelbuchstaben gekennzeichnet ( F ). Kräfte sind die Ursache von Bewegungen und Bewegungsänderungen. Dieser Teilbereich der Mechanik
wird als Dynamik bezeichnet. Im Gegensatz dazu beschreibt die Statik die Wirkung
und Verteilung von Kräften auf ruhende Körper, die sich in einem Kräftegleichgewicht befinden. Würde sich an einem Körper eine noch so kleine resultierende Restkraft ergeben, so würde der Körper gemäß den Axiomen von Newton beschleunigt
und damit in Bewegung versetzt.
2. Addition von Kräften
Jede wirkende Kraft kann bezüglich eines beliebig ausgerichteten Koordinatensystems in Teilkräfte zerlegt werden. Dies bedeutet aber in der Umkehrung, dass beliebige an einem gemeinsamen Angriffspunkt angreifende Kräfte durch eine Ersatzkraft ersetzt werden können. Diese Ersatzkraft wird durch geometrische Addition
(vektorielle Addition) der Einzelkräfte gebildet.
Fakultät Grundlagen
Ingenieurpädagogik
IP
Summer-School
Formal ergibt sich für die Vektoraddition der Teilkräfte hier:
r
r r r r r r
FRe s = F1 + F2 + F3 + F4 + F5 + F6 = 0
Je nach Richtung der Einzelkräfte ergeben sich bei der geometrischen Addition der
Kräfte so genannte Kräfteparallelogramme. Die Berechnung der resultierenden Kraft
in einem solchen Kräfteparallelogramm erfolgt mit Hilfe der trigonometrischen
Funktionen (Sinus, Kosinus und Tangens) oder im Fall rechtwinkliger Einzelkräfte
mit Hilfe des Satzes des Pythagoras.
3. Kraft und Gegenkraft (actio = reactio)
In der Natur treten Kräfte grundsätzlich paarweise auf, dies bedeutet, dass jede
Kraft eine Gegenkraft hervorruft. Newton nannte dieses Prinzip „actio = reactio“.
Man kann sich diesen Sachverhalt sehr schnell an einfachen Beispielen veranschaulichen: Liegt ein Körper mit einer gewissen Masse auf einem Tisch, so wirkt auf ihn
die Gewichtskraft FG = m . g. Dass diese Kraft stets wirkt, wissen wir, da ohne Tisch
der Körper auf den Boden fallen würde. Trotz dieser wirkenden Kraft verbleibt der
Körper aber in Ruhe. Dies ist aber nur dann der Fall, wenn am Körper keine resultierende Kraft wirkt. Also muss eine zweite Kraft auftreten, die die Gewichtskraft ausgleicht.
4. Linienflüchtigkeit von Kräften
Handelt es sich bei den von uns betrachteten Körpern um starre Körper, die sich
unter Wirkung der Kräfte nicht verformen, so können die am Körper angreifenden
Kräfte entlang ihrer Wirkungslinie beliebig verschoben werden. Dies bedeutet, dass
häufig zwei oder mehr an einem Körper angreifende Kräfte in einen gemeinsamen
Angriffspunkt verschoben werden können. Mit Hilfe der Addition von Kräften kann
daraus eine resultierende Kraft gebildet werden.
Fakultät Grundlagen
Ingenieurpädagogik
IP
Summer-School
F1
S
Fres
F2
5. Wirkung einer Kraft
5.1 Die Entstehung eines Moments
Man erkennt im vorangehenden Bild, dass die resultierende Kraft nicht im Schwerpunkt S des starren Körpers angreift. Verschiebt man ihren Angriffspunkt entlang
ihrer Wirkungslinie bis die Verbindungslinie zwischen Schwer- und Angriffspunkt
senkrecht auf der Wirkungslinie stehen, kann der Betrag des sich ergebenden Moments M sehr einfach berechnet werden.
M = FRes ⋅ r
Der Faktor r repräsentiert dabei den Abstand zwischen dem Schwerpunkt und dem
Angriffspunkt der Kraft. Die Richtung des entstehenden Moments kann mittels der
„Rechten-Hand-Regel“ unter Verwendung der drei orthogonal zueinander stehenden
Finger Daumen (Kraft), Zeigefinger (Abstand) und Mittelfinger (Moment) angegeben
Fakultät Grundlagen
Ingenieurpädagogik
IP
Summer-School
werden. Formal und im allgemeinen Fall berechnet sich das Moment aus dem Vektor- oder Kreuzprodukt des Kraft und des Abstandsvektors:
r r r r r
M = F × r = F ⋅ r ⋅ sin ϕ
Der Winkel ϕ definiert dabei den eingeschlossenen Winkel zwischen den beiden Vektoren, so dass im Fall der Rechtwinkligkeit der einfache Zusammenhang entsteht.
M
F1
S
r
Fres
F2
5.2 Die Entstehung einer Beschleunigung
Die unter 5.1 diskutiert Wirkung einer Kraft ist eigentlich ein spezieller Fall der nun
betrachteten Wirkung. Entsteht durch eine angreifende Kraft ein Moment an einem
starren Körper, so wird dieser radial beschleunigt (Rotation) bis die Wirkungslinie
der Kraft durch den Schwerpunkt des Körpers verläuft. Sobald diese Ausrichtung des
Körpers abgeschlossen ist, wird der Körper in Richtung der Kraft weiter beschleunigt
und führt eine geradlinige Bewegung aus (Translation). Dieser Sachverhalt, dass
Fakultät Grundlagen
Ingenieurpädagogik
IP
Summer-School
eine auf einen Körper wirkende Kraft stets eine Beschleunigung zur Folge hat, geht
auf Newton zurück. Das fundamentale Axiom lautet:
r
r
F = m⋅a
Durch die Vektoren wird klar, dass die entstehende Beschleunigung stets in Richtung der wirkenden Kraft hat. Paradebeispiel für die Beschleunigung eines Körpers
aufgrund einer angreifenden Kraft ist die Gravitationsbeschleunigung (Ortsfak-
r
tor) g , welche stets zum Erdmittelpunkt gerichtet ist. Die sie hervorrufende Kraft ist
die Massenanziehungskraft (Gravitationskraft) zwischen der Erde und jeder beliebigen Masse.
5.3 Die Entstehung einer Verformung
Die Verformung eines Körpers aufgrund einer angreifenden Kraft kann unmittelbar
mit der Beschleunigung als Wirkung erklärt werden. Hängt man an eine Feder mit
einer bestimmten Federkonstante k eine Masse m, so wird diese Masse aufgrund der
Gravitationskraft zum Erdmittelpunkt hin beschleunigt. Die Feder wir zunehmend
gedehnt und würde im Extremfall zerstört (unelastische Verformung), wenn nicht
mit zunehmender Dehnung der Feder eine rückstellende Kraft die beschleunigende
Kraft vermindern würde. Gehen wir von einer elastischen Verformung der Feder aus,
so gilt das Hookesche Gesetz:
r
r
FFeder = k ⋅ s
Die rückstellende Kraft der Feder erhöht sich also linear und sorgt so bei einer Auslenkung sGG für eine Kompensation der Gravitationskraft. Die resultierende Kraft und
damit die resultierende Beschleunigung sind im Gleichgewicht gleich Null.
6. Mögliche Experimente
Die Komponenten des Experimentiersatzes ermöglichen Ihnen Versuche und Experimente aus den folgenden Teilbereichen:
1. Wesen einer Kraft, Zerlegung und Addition
2. Schwerpunkt und Gleichgewichtslage
3. Kraftumformende Einrichtungen