Spannungsteiler / Ersatzspannungsquelle
Werbung

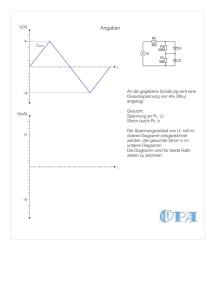
Spannungsteiler / Ersatzspannungsquelle zahlenpresse.de 12. Dezember 2012 1 Unbelasteter Spannungsteiler Die Gesammtspannung Uges fällt gemäß der Maschenregel über den beiden Widerständen R1 und R2 ab. Es gilt also Uges = U1 + U2 . Es soll nun die über R2 abfallende Spannung U2 in Abhängigkeit der Dimensionierung von R1 und R2 betrachtet werden. ges ò Iú R1 ÿ Uges R2 ÿ ò Uges = Iges · Rges = Iges · (R1 + R2 ) Da durch R1 und R2 der gleiche Strom Iges fließt, kann Iges hier noch wahlU1 U2 weise durch Iges = R oder Iges = R ersetzt werden. Da wir die Spannung U2 1 2 bestimmen wollen kommt nur letztere Substitution in Frage. Uges = U2 · (R1 + R2 ) R2 ⇔ 1 U2 = Uges · R2 R1 + R2 2 Belasteter Spannungsteiler ges R1 ÿ Iú Uges R2 RL ùÿ I2 ù IL Uges = Iges · Rges = (I2 + IL ) · (R1 + R2 ||RL ) Der Widerstand aus der Parallelschaltung R2 ||RL soll später berechnet werUL U2 und IL = R eingesetzt. Beachtet werden den. Hier werden erstmal I2 = R 2 L sollte dabei, dass aufgrund der Parallelität von R2 und RL über beiden Widerständen die gleiche Spannung abfällt und es gilt: U2 = UL . Uges = ( U2 UL + )·(R1 +R2 ||RL ) R2 RL Uges = UL · ( ⇔ Uges = ( UL UL + )·(R1 +R2 ||RL ) R2 RL 1 1 + ) · (R1 + R2 ||RL ) R2 RL Nach dem Erweitern der Brüche und Umformen nach UL ergibt sich dann: Uges = UL · ( Uges = UL · RL R2 + ) · (R1 + R2 ||RL ) R2 · RL R2 · RL R2 + RL ·(R1 +R2 ||RL ) R2 · RL ⇔ UL = Uges · R2 · RL (R2 + RL ) · (R1 + R2 ||RL ) Jetzt soll der Widerstand R2L = R2 ||RL aus den parallel liegenden Widerständen errechnet werden und in letztere Gleichung eingesetzt werden: 1 1 1 = + R2L R2 RL 1 R2 + RL = R2L R2 · RL ⇔ UL = Uges · UL = Uges · 1 RL R2 = + R2L R2 · RL R2 · RL ⇔ R2L = R2 · RL = (R2 ||RL ) R2 + RL R2 · RL (R2 + RL ) · (R1 + R2 ·RL R2 +RL ) R2 · RL · (R2 + RL ) (R2 + RL ) · (R1 · (R2 + RL ) + R2 · RL ) UL = Uges · R2 · RL R1 · R2 + R1 · RL + R2 · RL 2 3 Ersatzspannungsquelle Ziel der Ersatzspannungsquelle ist es, ausgehend vom unbelasteten Spannungsteiler eine neue Spannungsquelle Ui mit bekanntem Innenwiderstand Ri zu definieren. Vergleichsweise kann hier eine Batterie herangezogen werden von der zunächst auch einmal nur die Klemmenspannung bekannt ist. Der Innenwiderstand kann zwar nachgemessen werden, wie dieser sich aber zusammensetzt ist für den äußeren Betrachter nicht erfassbar. Erst an diese neue Spannungsquelle wird in Analogie zum belasteten Spannungsteiler die Last RL gemäß der folgenden Schaltung angeschlossen: IL ú Ri xyyyy z Ui - xyyyy z RL Für die Konstruktion der ESQ wird der Spannungsteiler im Leerlauf betrachtet. Dafür wurde bereits der folgende formale Zusammenhang aufgestellt: Ui = U2 = Uges · R2 R1 + R2 Im nächsten Schritt muss der Innenwiderstand Ri ermittelt werden. Dieser ergibt sich aus dem Widerstand an den Klemmen des unbelasteten Spannungsteilers, wobei die Spannungsquelle Uges kurzgeschlossen wird. Der Innenwiderstand kommt dann aus den parallel liegenden Widerständen R1 und R2 zu stande. Ri = R1 · R2 R1 + R2 Damit sind bereits alle Größen bekannt. Möchte man jetzt den Spannungsabfall über RL bestimmen, so hat man einen neuen Spannungsteiler bestehend aus Ri und RL zu berechnen. UL = Ui · RL Ri + RL Um die Richtigkeit dieser Gleichung zu proben genügt es Ui und Ri , wie oben aufgeschreiben einzusetzen. Damit finden wir die gleiche Formel, wie beim belasteten Spannungsteiler: UL = Uges · R2 · RL R1 · R2 + R1 · RL + R2 · RL Das Modell der Ersatzspannungsquelle ist gerade bei der Berechnung von größeren Netzwerken sehr hilfreich. 3