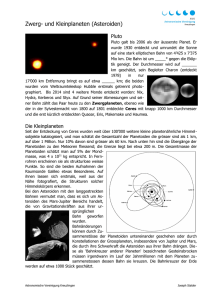
Ablenkung eines Asteroiden vom Kollisionskurs mit der Erde

Ablenkung eines Asteroiden vom
Kollisionskurs mit der Erde
Alexander Pichler, Simon Stadler
SS 2013
Inhaltsverzeichnis
1 Einleitung
2
2 Mathematische Formulierung
3
3 1.Modell
4
4 2.Modell
8
5 Ausblick
17
1
c
Abbildung 1: Don
Davis/Nasa
1 Einleitung
Vor 65 Millionen Jahren hat der Einschlag eines Asteroiden mit einem Durchmesser von
ungefähr 10 km auf der heutigen Yucatán-Halbinsel in Mexiko die Ära der Dinosaurier
beendet und große Verwüstung auf der Erde verursacht, ca. 75 % allen Lebens auf der
Erde wurde zerstört. Heute beschäftigt sich die Wissenschaft unter anderem mit der
Frage, was man tun kann, um zu verhindern, dass sich so ein Ereignis wiederholt. Ein
möglicher Ansatz wäre, den Asteroiden mit einer gezielten nuklearen Sprengung soweit
von seinem Kurs abzulenken, dass er der Erde nicht mehr gefährlich werden kann.
Ziel unseres Projekts ist es, dieses Szenario mathematisch zu modellieren und dabei auf
folgende Fragestellungen näher einzugehen:
• Welche Flugbahn bzw. Geschwindigkeit muss der Asteroid an einer gegebenen Position erreichen, um die Erde zu verfehlen?
• Wo und wie stark muss ein Impuls gesetzt werden, um den Asteroiden auf die
gewünschte Flugbahn zu bringen?
• Wie verhält sich der Asteroid unter der Gravitationskraft verschiedener Körper?
• Wo liegen die physikalischen Grenzen, d.h. bei welcher Entfernung des Asteroiden
von der Erde bzw. bei welcher Geschwindigkeit des Asteroiden ist keine Rettung
mehr möglich?
In unserer Ausarbeitung werden wir dabei versuchen, Gleichungen für die Flugbahn
des Asteroiden herzuleiten und diese anschließend für ausgewählte Startwerte numerisch
zu lösen. Danach wollen wir unsere Ergebnisse graphisch darzustellen und eine kurze
Interpretation dazu abgeben.
2
2 Mathematische Formulierung
In dieser Ausarbeitung haben wir uns für ein Top-Down Modell entschieden, das auf
physikalischen Gesetzen beruht. Dabei werden wir folgende Variablen benötigen:
RE ..........Radius der Erde (≈ 6.378km)
RA ..........Radius des Asteroiden
MA ..........Mittelpunkt des Asteroiden
PA ..........Anschusspunkt des Asteroiden
hmin ..........minimaler Abstand, des Asteroiden von der Erde (Mondentfernung ≈ 384.400km)
Rmin ..........Abstand des Asteroidenmittelpunkts zum Ermittelpunkt
mE ..........Masse der Erde (≈ 5, 9736 · 1024 kg)
mS ..........Masse der Sonne (≈ 1, 989 · 1030 kg)
mA ..........Masse des Asteroiden
F..........Kraft
p..........Impuls
m3
G..........Gravitationskonstante ≈ 6, 673 · 10−11 kg·s
2
x1 (t)
x(t)..........Position des Asteroiden relativ zur Erde, x(t) =
∈ R2
x2 (t)
x0,1
∈ R2
x0 ..........Startposition des Asteroiden relativ zur Erde, x0 =
x0,2
xE (t)..........Position der Erde
xS (t)..........Position der Sonne
y(t)..........Position des Asteroiden
Im ersten Teil unserer Ausarbeitung werden wir den Spezialfall betrachten, dass unser
Universum nur aus dem Asteroid und der Erde besteht. Mit Hilfe der Newton’schen
Bewegungsgleichungen werden wir die Flugbahn des Asteroiden studieren und erste Beobachtungen anstellen.
In weiterer Folge werden wir dann unser System um einen weiteren Körper, z.B. der
Sonne, erweitern und versuchen ein Gespür dafür zu bekommen, welchen Einfluss ein
weiterer Körper auf unser System hat. Hierfür werden wir uns auf ein eingeschränktes
Drei-Körper-Problem stützen, d.h. zwei Massen, die Erde und ein weiterer Körper, kreisen dabei um ihren gemeinsamen Schwerpunkt und eine dritte Masse, der Asteroid,
beeinflusst diese jedoch aufgrund seiner vergleichsweise verschwindend geringen Masse
nicht in deren Bewegung.
Zum Schluss werden wir noch eine Überlegung anstellen, wie man nun mit ähnlichen
Argumenten wie in den beiden Spezialfällen, einerseits dem Zwei-Körper-Problem und
andererseits dem eingeschränkten Drei-Körper-Problem, die Flugbahn des Asteroiden in
einem ganzen Sonnensystem, d.h. mit N verschiedenen Körpern, theoretisch herleiten
könnte.
3
3 1.Modell
In unserem 1.Modell werden wir einige Vereinfachungen vornehmen, um zunächst die
Grundprinzipien und physikalischen Zusammenhänge besser verstehen und nachvollziehen zu können. Folgende Annahmen werden daher von uns getroffen:
• Sowohl die Erde als auch der Asteroid seien Massenpunkte im Raum und die Erde
wird als Fixpunkt im Weltraum betrachtet, der seine Position nicht verändert.
• Es gibt keine weiteren Körper im Raum.
• Sowohl Erde als auch Asteroid haben Kugelgestalt.
• Der Asteroid ist unzerstörbar.
• Der Asteroid steuert senkrecht auf die Erde zu.
• Es gibt eine Distanz zwischen Erde und Asteroid ab der die Erde als gerettet
angesehen wird (ca. 107 km)
Wir reduzieren unser Modell auf ein 2-dimensionales System. Dabei befindet sich die
Erde im Ursprung unseres Koordinatensystems und der Asteroid auf der positiven yAchse.
x0,1
Weiters sei die Startposition des Asteroiden mit x0 =
∈ R2 gegeben.
x0,2
Unser Ziel in diesem Modell ist es die Flugbahn des Asteroiden zu bestimmen.
Hierfür verwenden wir das physikalische Gesetz
F = mA · |ẍ(t)|,
ẍ(t).....Beschleunigung.
Da die Kraft F in Richtung der Erde, also zum Ursprung, zeigt, müssen wir den negierten
und normierten Ortsvektor zwischen Erde und Asteroid verwenden. Das ergibt nun nach
Umformen der obigen Gleichung
ẍ(t) = −
x
F
·
|x| mA
und somit erhalten wir eine nichtlineare Bewegungsgleichung der Form
x(t)
F
ẍ(t) + p
·
= 0.
2
2
x1 (t) + x2 (t) mA
Nun verwenden wir das Newton’sche Gravitationsgesetz
F =G·
mE · mA
.
|x(t)|
4
Einsetzen dieses Gesetzes in unsere Bewegungsgleichung ergibt
ẍ(t) = −
x(t)
· G · mE .
|x(t)|3
Die Bewegungsgleichung hängt also nicht mehr von der Masse des Asteroiden ab. In
diesem Modell geben wir uns mit einer numerischen Lösung zufrieden. Im nächsten
Kapitel (2.Modell) werden wir unser System mit der Sonne als weiterem Körper erweitern
und eine analytische Lösung, soweit wie möglich, liefern.
Abbildung 2: Mögliche Flugbahnen des Asteroiden im vereinfachten Fall, bei verschiedenen
Anflugswinkeln
5
Wir möchten uns nun mit der Frage beschäftigen, welcher Impuls benötigt wird um den
Asteroiden bei gegebener Anfangsgeschwindigkeit ẋ0 auf eine bestimmte Flugbahn zu
bringen, d.h. eine gewünschte Endgeschwindigkeit und Richtung zu erreichen. Hierfür
verwenden wir die physikalische Formel für den Impuls p
p = mA · (ẋ − ẋ0 ) ,
wobei (ẋ − ẋ0 ) ∈ R2 die Veränderung der Geschwindigkeit des Asteroiden beschreibt.
Im Anschusspunkt des Asteroiden PA soll nun ein Impuls p gesetzt werden, sodass der
Asteroid seine Bahn ausreichend verändert um die Erde zu verfehlen. Dafür haben wir
zur Bestimmung der nötigen Anfangsgeschwindigkeit und Flugrichtung des Asteroiden
das Randwertproblem
(
x(t)
ẍ(t) = − |x(t)|
3 · G · mE
x(0) = x0 ,
x(t0 ) = x1
Hierbei ist x0 die Startposition des Asteroiden, x1 ist die Position des Asteroiden mit
minimaler Distanz zur Erde und t0 ist die Zeit, die der Asteroid ohne äußere Einflüsse
benötigen würde um den Sicherheitsabstand zur Erde zu unterschreiten.
Abbildung 3: Ablenkung des Asteroiden vom Kollisionskurs mit der Erde
Auf Abbildung 3 ist ein konkreter Fall der Impulseinwirkung zu sehen. Der kleine schwarze Kreis stellt hier den nötigen Mindestabstand zwischen Asteroid und Erde dar, und
der größere schwarze Kreis jede Distanz, ab der die Erde als gerettet gilt. Die blaue Linie
beschreibt die Bahn des Asteroiden ohne äußere Einflüsse.
6
Die hierbei verwendeten Startwerte sind
0
0
x0 =
und v0 =
107
−10.8991
für Startposition und Startgeschwindigkeit, und sind in km beziehungsweise km/s gegeben. Dafür wurde der Anfangswert v0 der prognostizierten Einschlagsposition und
Einschlagsgeschwindigkeit berechnet.
Es ist zu bemerken, dass sich der Asteroid im unbeeinflussten Fall senkrecht auf die Erde zubewegt. Diese Annahme wurde deshalb getroffen, weil in diesem Fall der benötigte
Impuls am größten ist, die Situation also als worst case betrachtet werden kann.
Die Bahn des Asteroiden nach äußerer Impulseinwirkung wird durch dir rote Linie
dargestellt. Der berechnete nötige absolute Geschwindigkeitsunterschied liegt hier bei
0, 4008 km/s, was bei einem Asteroid mit einer Masse von 500kg einem benötigten
Impuls von 200.400 kg · m/s entspricht.
Ein Kritikpunkt dieses Modells ist, dass es sehr vereinfacht und daher nicht sehr realistisch ist. Wir gehen beispielsweise davon aus, dass es außer der Erde keinen weiteren
Körper gibt, der Gravitation auf den Asteroiden ausübt und somit würde der Asteroid
früher oder später mit der Erde kollidieren.
7
4 2.Modell
In diesem Modell erweitern wir unser 1.Modell:
• Die Sonne sei nun das Zentralgestirn im Zentrum unseres Systems.
• Die Erde kreise um die Sonne und übe ebenfalls Gravitation auf die Sonne aus,
d.h. es liegt ein Zweikörperproblem vor.
• Der Asteroid wird sowohl von der Erde als auch der Sonne angezogen.
Wir möchten nun die Flugbahn des Asteroiden bestimmen. Hierfür überlegen wir uns
zunächst einmal, wie die Bahnen der Sonne und der Erde unter gegenseitiger Gravitation
aussehen.
Wie wir uns bereits überlegt haben, gilt für die Bahn der Sonne
ẍS = −
xS − xE
· G · mE
|xS − xE |3
ẍE = −
xE − xS
· G · mS .
|xS − xE |3
und analog für die Erde
Um dieses System von Differentialgleichungen 2.Ordnung zu lösen, benötigen wir die
sogenannten Jacobi-Koordinaten
m S xS + m E xE
mS + mE
r := xS − xE ,
Υ :=
wobei r den relativen Abstand der Sonne zur Erde und Υ den Massenschwerpunkt bezeichnet. Weiters gilt
Ϋ =
mS ẍS + mE ẍE
= 0,
mS + mE
da
mS ẍS = FE,S ,
mE ẍE = FS,E = −FE,S ,
wobei FE,S die Kraft bezeichnet, die die Erde auf die Sonne ausübt und FS,E die Kraft
der Sonne auf die Erde ist. Mit dem Newton’schen Wechselwirkungsprinzip folgt, dass die
Kräfte vom Betrag her gleich groß aber entgegengesetzt sind und sich somit in Summe
aufheben. Somit bewegt sich der Schwerpunkt gleichförmig geradlinig (oder bleibt in
Ruhe).
Sei im Folgenden M := mS + mE die Gesamtmasse von Sonne und Erde. Es gilt folgende
Beziehung
r̈ = ẍS − ẍE = −
r
· G · M.
|r|3
Diese Gleichung beschreibt die Relativbewegung eines fiktiven Teilchens mit der redumE
zierten Masse µ = mmSS+m
im Schwerefeld einer größeren Masse unter dem Einfluss der
E
8
Kraft F = µ · r̈. Dies ist eine Zentralkraft, d.h. eine Kraft, die immer auf einen festen
Punkt (das Kraftzentrum) bezogen ist und auf diesen hin- oder weggerichtet ist, somit
in Richtung des Vektors r zeigt.
Eine wichtige Erkenntnis ist, dass für Zentralkräfte der Drehimpuls nach Betrag und
Richtung erhalten bleibt, denn es gilt für den Drehmoment T , der als vektorielles Skalarprodukt von Kraft und Radiusvektor gegeben ist
T = F × r = (µ · r̈) × r = −µ · G · M ·
1
· (r × r) = 0
|r|3 | {z }
(1)
=0
und somit muss der Drehimpuls während der Bewegung konstant bleiben, da der Drehmoment ein Maß für die Drehwirkung der Kraft F ist. Diese Größen bleiben somit bei
einer Verschiebung des Inertialsystems erhalten.
Für den Drehimpuls L(t) gilt
L(t) = r(t) × p(t) = µ · (r × ṙ),
(2)
wobei p(t) der Impuls ist. Somit erhalten wir nach Ableitung nach der Zeit die Bewegungsgleichung für den Drehimpuls in der Gestalt
dL(t)
d
d
= (r(t) × p(t)) = (µ · (r × ṙ)) = µ · (ṙ| {z
× ṙ} +r × r̈) = r × F = T.
dt
dt
dt
=0
Wegen (1) gilt dL(t)
dt = T = 0 und damit ist L(t) konstant. Für F 6= 0 kann T nur 0 sein,
wenn F parallel zu r verläuft und daher verläuft die Bewegung in einer Ebene.
Um die Bahnbewegung beschreiben zu können, verwenden wir nun die Polarkoordinaten
(ρ, φ).
Mit dem 2.Keplerschen Gesetz (Der Fahrstrahl von der Sonne zum Planeten überstreicht
in gleichen Zeiten gleiche Flächen.) gilt nun folgende Beziehung für die überstrichene
Fläche A unter Verwendung von (2)
1
(2) L
A = |r × ṙ| =
2
2µ
Kepler
=
ρ2 φ̇
= const
2
und damit insbesondere
ṙ × r = ρ2 φ̇
und
L = µρ2 φ̇.
(3)
Nun verwenden wir den Energieerhaltungssatz der Mechanik, der besagt, dass in einem
abgeschlossenen System keine Umwandlung von mechanischer Energie in andere Energieformen erfolgt und daher zu jedem Zeitpunkt die Summe aus potentieller Energie
Epot und kinetischer Energie Ekin eines Körpers konstant ist. Mathematisch formuliert
E = Epot + Ekin .
Für die Bewegung eines Teilchens mit Masse µ und Geschwindigkeit υ gilt Ekin = 12 µυ 2
und insgesamt folgt daher
1
E = Epot + µυ 2 .
2
9
(4)
Sei nun der Aufenthaltsort des Teilchens mit ~x := (x1 , x2 ) gegeben. Durch die Polarkoordinatentransformation ergeben sich nun folgende Beziehungen
x1 = ρcos(φ),
x2 = ρsin(φ)
und
q
ρ = x21 + x22 ,
φ = arctan(x2 /x1 ).
Weiters seien e1 , e2 die Einheitsvektoren im kartesischen Koordinatensystem. In unserem neuen Koordinatensystem, das durch die Polarkoordinaten gegeben ist, seien die
Einheitsvektoren mit eφ und eρ gegeben, wobei diese orthogonal aufeinander stehen (sh.
Abbildung 4).
Abbildung 4: Koordinatensystemtransformation
Unser Ziel ist es nun, eine Beziehung zwischen den Einheitsvektoren im kartesischen
Koordinatensystem und den Einheitsvektoren im neuen Koordinatensystem herzustellen.
Hierfür betrachten wir das Differential des Ortsvektors ~x und erhalten nach einigen
Umformungen
d~x = dx1 e1 + dx2 e2
∂x1
∂x1
∂x2
∂x2
=
dρ +
dφ e1 +
dρ +
dφ e2
∂ρ
∂φ
∂ρ
∂φ
= (cos(φ)dρ − ρ sin(φ)dφ) e1 + (sin(φ)dρ + ρ cos(φ)dφ) e2
= (cos(φ)e1 + sin(φ)e2 ) dρ + ρ (− sin(φ)e1 + cos(φ)e2 ) dφ
:= dρeρ + ρdφeφ .
10
Somit gelten die Beziehungen
eρ = cos(φ)e1 + sin(φ)e2
eφ = − sin(φ)e1 + cos(φ)e2
und eρ und eφ sind tatsächlich orthogonal aufeinander, denn
eρ · eφ = (cos(φ)e1 + sin(φ)e2 ) · (− sin(φ)e1 + cos(φ)e2 )
cos(φ)
− sin(φ)
=
·
sin(φ)
cos(φ)
= cos(φ)(− sin(φ)) + sin(φ) cos(φ)
= 0.
Es ergibt sich also folgende Flugbahn des Teilchens in Abhängigkeit von der Zeit t
~x(t) = x1 (t)e1 + x2 (t)e2 .
Für die Geschwindigkeit betrachten wir nun die Ableitung nach der Zeit und beobachten
υ = ∇t x = ρ̇eρ + ρφ̇eφ .
Setzen wir dies nun in (4) ein, erhalten wir für die Gesamtenergie E
1
E = Epot + µ(ρ̇2 + ρ2 φ̇2 ),
2
wobei 12 µρ̇2 dem Radialanteil der kinetischen Energie und
1 2 2 (3) 1 2 L2
1 L2
µρ φ̇ = µρ 2 4 =
2
2
µ ρ
2 µρ2
dem Winkelanteil der kinetischen Energie entspricht.
Weiters ist die potentielle Energie gegeben durch die Formel
Epot = −
GM µ
.
ρ
(5)
Nach Umformen erhalten wir
E − Epot
− ρ2 φ̇2
µ
E − Epot
= 2
− ρ2 .
2
µφ̇
ρ̇2 = 2
ρ̇2
φ̇2
bzw.
2
Wegen (3) können wir nun auf der rechten Seite φ̇2 durch µL2 ρ4 ersetzen und erhalten
E − Epot
E − Epot
ρ̇2
1
2
4
=2
− ρ = ρ 2µ
− 2 .
2
L2
ρ
φ̇2
µ L2 4
µ ρ
11
Nun führen wir folgende Parametrisierung durch
dφ
dt
dρ
dφ
dρ
dt
=
dρ dφ
dφ dt
und nach formaler Division
ρ̇
.
φ̇
durch
ergibt sich nun
=
Setzen wir diese Parametrisierung nun in die obige Gleichung ein, erhalten wir nun eine
Bahnkurve mit folgender Gestalt
dρ
dφ
2
4
=ρ
E − Epot
1
2µ
− 2
2
L
ρ
.
Ersetzen wir nun Epot durch die in (5) dafür ermittelte Formel bekommen wir für unsere
Bahngleichung
1 dρ
ρ2 dφ
2
2µ
= 2
L
GM µ
1
E+
− 2.
ρ
ρ
Um diese Gleichung auf eine einfachere Gestalt zu bringen, definieren wir eine Funktion
1
. Insgesamt folgt nun
σ(φ) := ρ(φ)
dσ
dφ
2
dσ 2 2µ
= −
= 2 (E + GM µσ) − σ 2 .
dφ
L
Durch Umformen erhalten wir nun
2µ
2Eµ 2σGM µ2
2
(E
+
GM
µσ)
−
σ
=
+
− σ2.
L2
L2
L2
4
L
Erweitern der ersten zwei Terme mit G2 M
2 µ4 und danach Addieren von 0 liefert
2
L4
2σL2
2
1 + G2EL
2
2
4
2 M 2 µ3 + GM µ2 − 1
2Eµ 2σGM µ
G M µ
2
−σ =
− σ2
+
L4
L4
L2
L2
2
2 4
G M µ
G2 M 2 µ4
Unter Einführung der Konstanten
L2
ζ :=
,
GM µ2
s
ε :=
1+
2EL2
G 2 M 2 µ3
ergibt sich nun eine wesentlich einfachere Darstellung
1+
2σL2
2EL2
+ GM
G2 M 2 µ3
µ2
4
L
G2 M 2 µ4
−1
− σ2 =
ε2
2σ
ε2 + 2σζ − 1
1
2
2
−
σ
=
−
σ
−
+
ζ2
ζ2
ζ
ζ2
ε2
1 2
= 2 − σ−
.
ζ
ζ
Daher haben wir nun insgesamt eine Differentialgleichung folgender Gestalt erhalten
dσ
dφ
2
ε2
1 2
= 2 − σ−
.
ζ
ζ
12
⇒r
ε2
ζ2
σ̇
2 = 1
1
− σ−ζ
Zσ
⇒t+c=
σ− ζ1
1
r
2 dz =
ε2
1
− z−ζ
ζ2



t + c =⇒ arctan 
r

Z
ε2
ζ2
1
q
ε2
ζ2
− u2
σ− 1

du = arctan  q
ζ
u
ε2
ζ2
− u2

σ − ζ1


2 
− σ − ζ1
σ − ζ1
2
ε2
1
−
σ
−
ζ
ζ2
2
σ − ζ1
sin2 (t + c)
⇒
=
2
cos2 (t + c)
ε2
1
−
σ
−
ζ
ζ2
2
ζ2
1
2
σ
−
2
ζ
sin (t + c)
ε
=
⇒
2
2
2
1 − sin (t + c)
1 − ζε2 σ − ζ1
1
ζ
σ−
⇒ sin(t + c) =
ζ
ε
1
1 + ε sin(t + c)
⇒ σ = sin(t + c) + =
ζ
ζ
ζ
⇒ tan(t + c) = r
Als Lösung dieser Differentialgleichung erhalten wir daher
σ(φ) =
1 + ε sin(φ + c)
,
ζ
wobei c ∈ R, und nach Rücksubstitution von ρ(φ) =
ρ(φ) =
1
σ(φ)
ζ
.
1 + ε sin(φ + c)
Nun möchten wir jedoch wieder mit den kartesischen Koordinaten weiterarbeiten, weshalb wir folgende Rücktransformationen vornehmen
x = ρ(φ) cos(φ) + d,
wobei d ∈ R.
13
y = ρ(φ) sin(φ),
Es ergeben sich für x und y, wenn wir sämtliche Resubstitutionen vornehmen
L2
GM µ2
x=
1+
q
1+
2EL2
G2 M 2 µ3
cos(φ) + d
L2
GM µ2
y=
1+
q
1+
2EL2
G2 M 2 µ3
(6)
sin(φ + c)
sin(φ)
sin(φ + c)
Zusammengefasst ergibt sich nun:
Die Bahn des Asteroiden y(t) ist gegeben durch
ÿ(t) = −
y−x
y
mS G −
mE G
3
|y|
|y − x|3
(7)
wobei die Bahn der Erde x(t) durch
ẍ(t) = −
x
mS G
|x|3
beschrieben wird.
Die Lösung der obigen Differentialgleichung haben wir bereits in (6) ermittelt. Setzen
wir diese in (7) ein, erhalten wir für die Bahn des Asteroiden unter dem Einfluss von
Sonne und Erde eine Bahngleichung der Form

y¨1
y¨2
y1
y2
y1
y2



−


(t) = − 
mS G− y1 3
y2 


y1
−

y2

r
1+ 1+
2EL2
sin(φ+c)
G2 M 2 µ3
2
L
GM µ2
r
1+ 1+
2EL2
G2 M 2 µ3
cos(φ) + d 




sin(φ) 
sin(φ+c)
3 mE G
r
cos(φ)
+
d

2EL2

1+ 1+ 2 2 3 sin(φ+c)

G M µ

L2

GM µ2
r
sin(φ) 
2
1+ 1+ 22EL2 3 sin(φ+c)
G M µ
L2
GM µ2
Diese Differentialgleichung lösen wir nur mehr numerisch.
14

L2
GM µ2
Abbildung 5: Mögliche Kollsisionsbahnen des Asteroiden im 3-Körper-Modell
In Abbildung 5 sind drei mögliche Bahnen des Asteroiden im 3-Körper-Modell dargestellt. Die dafür verwendeten Anfangswerte wurden wieder numerisch konstruiert.
Der schwarze Kreis stellt hier den nötigen Sicherheitsabstand zwischen Erde und Asteroid dar. Die vertikalen Linien beschreiben die Umlaufbahn der Erde um die Sonne, welche
sich im Ursprung befindet, aus Saklierungsgründen jedoch nicht in der Grafik angezeigt
wird. Die Flugbahnen der Asteroiden sind durch die dünneren Linien gekennzeichnet und
deren Verletzungspunkte mit dem nötigen Sicherheitsabstand werden durch die blauen
Sterne dargestellt. In diesen Szenarien wird durch die verwendeten Startwerte angenommen, dass sich Sonne, Erde und Asteroid ungefähr auf einer Linie befinden.
Es ist zu erkennen, dass der Asteroid bei Bahn 3 erst nachdem er bereits an der Erde vorbei geflogen ist den Sicherheitsabstand unterschreitet. Das passiert deshalb, weil
sich die Erde trotzdem noch dem Asteroiden annähert, und dieser durch den geringen
Abstand stark von der Erde angezogen wird. Der Asteroid entfernt sich deshalb nicht
schnell genug von der Erde und wird trotzdem als gefählich eingestuft.
15
Wir haben uns auch im 3-Körper-Modell mit der Frage beschäftigt, welcher Impuls nötig
ist, um den Asteroiden auf eine günstige Bahn zu lenken. Dafür haben wir ein Programm
in Matlab geschrieben, das bei gegebener Startposition und Startgeschwindigkeit den minimalen benötigten Impuls in eine vorgegebene Richtung berechnet, sodass der Asteroid
auf seiner Flugbahn den vorgegebenen Sicherheitsabstand zur Erde nicht unterschreitet.
Abbildung 6: Berechnete ideale Flugbahnen des Asteroiden
Beim 3-Körper-Modell ist das Finden einer geeigneten Impulsrichtung schwieriger als
beim 2-Körper-Modell, da sich die Erde bewegt. Der Impuls kann beispielsweise die
Annäherungsgeschwindigkeit des Asteroiden verringern, wodurch sich die Erde weiter
bewegen kann, bevor der Asteroid sich annähert.
In Abbildung 6 beschreibt Bahn 0 die Bahn des Asteroiden ohne äußere Impulseinwirkung. Für dieses Beispiel haben wir drei mögliche Impulsrichtungen versucht: in Richtung
der Erdbewegung (Impuls 1), entgegen der Erdbewegung (Impuls 3) und sowohl entgegen der Erdbewegung als auch entgegen der Flugrichtung des Asteroiden (Impuls 2).
Die dafür berechneten nötigen Impulskräfte sind 3.708.063 kg·m/s (Impuls 1), 410.304 kg·
m/s (Impuls 2) und 2.673.790 kg · m/s (Impuls 3). Man erkennt sofort, dass unter diesen
drei Richtungen die zweite die idealste ist. Weiters ist erkennbar, dass der nötige Impuls
im Vergleich zum 2-Körper-Modell entscheidend größer ist. Dies lässt sich dadurch erklären, dass durch die Sonne eine größere Anziehungskraft vorherrscht, der mittels dem
Impuls entgegengewirkt werden muss.
16
5 Ausblick
Auch unser 2.Modell ist sehr unrealistisch, da wir uns lediglich auf ein 3-Körper-Problem
beschränkt haben. Wir haben jedoch gesehen, dass selbst dieses Problem nicht mehr analytisch lösbar ist. Wenn wir nun ein allgemeines N-Körper-Problem betrachten, kann die
Bewegungsgleichung für eine Masse mi unter dem Einfluss der gegenseitigen Gravitationskräfte explizit angegeben werden:
mi r¨i = −
n
X
Gmi mk
k=1
ri − rk
,
3
rik
wobei ri der Abstand der Masse mi vom Schwerpunkt ri ist und der Abstand der Massen
mi , mk untereinander mit rik bezeichnet wird. Wie man sieht bekommt man hier wiederum ein nichtlineares System von Differentialgleichungen 2.Ordnung, das es zu lösen gilt.
Der Schwerpunktsatz besagt nun, dass wenn alle diese Bewegungsgleichungen addiert
werden, 0 herauskommen muss, d.h.
X
mi r¨i = 0,
da es für jeden Term rk − ri einen entsprechenden Term ri − rk gibt, die sich somit
gegenseitig aufheben. Wenn man obige Gleichung nun zweimal integriert, bekommt man
X
mi r¨i = at + b,
wobei a, b ∈ R. Somit ist der Schwerpunkt des N-Körper-Problems stets in Ruhe oder geradliniger Bewegung. Dies haben wir auch schon in unserem Modell beobachten können.
Eine weitere Beobachtung liefert der Drehimpulssatz: Analog wie in Gleichung (2) gilt
nun
X
mi ri × r˙i = const.
Weiters haben wir gesehen, dass auch die Energie eine entscheidende Rolle spielt. Der
Energiesatz besagt, dass bei Bewegung eines Teilchens in einem konservativem Kraftfeld,
d.h. in einem Kraftfeld, in dem keine Energie verloren geht“, die Gesamtenergie genau
”
der Summe von potentieller und kinetischer Energie entspricht. Es gilt, dass die Kraft
der negative Gradient der potentiellen Energie ist, d.h. F = −∇Epot .
Wie in Gleichung (5) können wir die potentielle Energie durch
Epot = −G
X mi mk
i,k
ri,k
ausdrücken und somit gilt insgesamt
X
mi r¨i = ∇G
X mi mk
i,k
17
ri,k
.
In unseren Modellen haben wir nun durch geeignete Transformationen unter Verwendung
dieser physikalischen Beziehungen die Differentialgleichungen zumindest teilweise lösen
können.
Das numerische Modell zur Berechnung des nötigen Impulses ließe sich problemlos um
mehrere weitere Körper erweitern, allerdings würde dies zu einer enormen Steigerung
der Berechnungszeit führen. Hierfür müssten nur weitere Konstanten eingeführt und die
Differentialgleichungen angepasst werden.
Es ist allerdings zu beachten, dass sich auch diese zusätzlichen Körper in dem Modell
nur auf einer Ebene bewegen dürfen. Ansonsten müsste man das Modell um die dritte
Dimension erweitern.
18
Literatur
[1]
Arnold Hanslmeier. Einfhrung in Astronomie und Astrophysik. 2. Auflage. Spektrum
Akademischer Verlag, 2011.
[2]
Ewald Schachinger. Elementare Newtonsche Mechanik. Juni 2013. url: http://
itp.tu-graz.ac.at/LV/ewald/AM/am2.pdf.
[3]
Ewald Schachinger. Etwas Mathematik. Juni 2013. url: http://itp.tu-graz.ac.
at/LV/ewald/AM/amap1.pdf.
[4]
Juni 2013. url: http://en.wikipedia.org/.
19