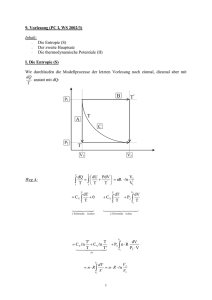
2.3 Flüssige Kristalle 3. Thermodynamik

12
Flüssigkeit sofort verschwinden, bei nicht-Newtonschen Flüssigkeiten erhält man exponentielle
Abklingkurven, deren Zeitkonstanten u.a. die Länge von Aggregaten in der Lösung zu ermitteln ermöglicht.
2.3 Flüssige Kristalle
Bestimmte Substanzen bilden oberhalb vom Schmelzpunkt zunächst trübe Flüssigkeiten aus,
die erst bei deutlich höheren Temperaturen klar werden (Klärpunkt). Die trüben Flüssigkeiten
sind Flüssigkristalle, in welchen die Moleküle eine gewisse Ordnung ausweisen. Es sind zumeist Moleküle mit einem stäbchenförmigen, starren Mittelteil (z. B. Biphenyle), die an einem
oder beiden Enden flexible Gruppen tragen (z.B. aliphatische Ketten). Aus der festen Phase
kommend gelangt man bei steigender Temperatur zunächst zu vergleichsweise hochgeordneten
smektischenPhasen, die Schichten parallel angeordneter solcher Moleküle enthalten. Cholesterische Phasen entstehen aus Schichten, die Moleküle mit einer Vorzugsrichtung aufweisen,
wobei sich diese Vorzugsrichtung mit jeder Schicht um einen bestimmten Winkel verschiebt.
Nach einer von diesen Winkel abhängigen Zahl von Schichten liegt wieder die Vorzugsrichtung der untersten Schicht vor (Ganghöhe). Die geringste Ordnung liegt bei nematischen Phasen vor, in denen die länglichen Moleküle zwar eine Vorzugsrichtung aber keine Ordnung
senkrecht zu dieser Vorzugsrichtung zeigen. Man kann sich vorstellen, dass in solchen Systemen verschiedene Viskositäten in den drei Raumrichtungen auftreten, die nur mit speziellen
Messgeräten gemessen werden können, aber für bestimmte Anwendungen bekannt sein sollten.
smektisch
cholesterisch
nematisch
(Abb. aus Wikipedia)
Wenn die Moleküle eine gewisse Polarität oder Polarisierbarkeit aufweisen, lassen sich die
flüssigen Kristalle im elektrischen Feld ausrichten. So wird bei angelegtem Feld aus einem
cholesterischen ein nematischer Flüssigkristall (SCHADT-HELFRICH-Effekt), der dadurch für
(linear polarisiertes) Licht durchlässig wird – dieser Effekt ist die Basis für moderne, preiswerte Anzeigegeräte aller Art (Displays).
3. Thermodynamik
3.1 Entropie in der Nähe des absoluten Nullpunkts (3. Hauptsatz)
Man erinnere sich an die Definition der Entropie ds = dqrev/T (mit Hilfe des Carnot-Prozesses
im Teil I), wobei dqrev in praktischen Fällen durch (cp/T) dT oder (cv/T) dT des untersuchten
Stoffes gegeben ist.
NERNST fand Anfang des 20. Jahrhunderts, dass die Differenzen der molaren Wärmekapaziäten
(Cp oder Cv) zwischen Edukten und Produkten einer Reaktion mit fallender Temperatur immer
13
kleiner wurden. Entsprechend geringer wurden die zugehörigen Reaktionsentropien ∆RS. Er
folgerte daraus (insbesondere für die Reaktionen reiner kristalliner Festkörper), dass
lim ∆S = 0
(3-1),
T →0
dass also die Reaktionsentropie bei Annäherung an den absoluten Nullpunkt gegen Null strebt.
Diese Folgerung ist als NERNSTsches Wärmetheorem bekannt. PLANCK überarbeitete dieses
und konnte formulieren
lim S = 0
(3-2),
T →0
also dass die Entropie selbst beim absoluten Nullpunkt (für ideale Festkörper) verschwindet.
Dies wird als 3. Hauptsatz der Thermodynamik bezeichnet.3
Dieser Hauptsatz ist problematischer als die ersten beiden. Streng genommen kann die Entropie nur bei ideal kristallisierten Festkörpern verschwinden, bei welchen jedes Atom seinen festen Platz hat. Zahlreiche Stoffe kristallisieren aber nicht ideal (wechselnde Molekülorientierung, Glaszustand) und in der statistischen Thermodynamik verschwindet die Entropie bei kristallisierten Mischelementen wegen unterschiedlicher Anordnungen der Isotope nicht.
Der Hauptsatz ermöglicht jedoch die Ermittlung absoluter Entropien nach
T
T
Cp
C
S (T ) = S (T = 0) + ∫
dT ( bzw. S (T ) = S (T = 0) + ∫ v dT )
(3-3),
T
T
0
0
weil wir mit dem 3. Hauptsatz S(T=0) = 0 setzen können. Dazu sind – wie im Teil I gesagt –
ggf. Phasenumwandlungsentropien und unterschiedliche Werte der Molwärmen (spezifischen
Wärmen) Cp und Cv in den verschiedenen Aggregatzuständen zu berücksichtigen. Da Cp und
Cv auch innerhalb von Phasenbereichen nicht konstant sind, gelten obige Beziehungen entweder nur für einen eingeschränkten Temperaturbereich oder es muss bei der Integration die
Temperaturabhängigkeit der Molwärmen berücksichtigt werden. Bei hinreichend tiefen Temperaturen folgt die Molwärme Cv von perfekten Kristallen (nach einer Theorie von DEBYE)
dem folgenden Grenzgesetz (T3-Gesetz)
3
12 π 4  T 
lim Cv =
⋅  ⋅R.
(3-4).
T →0
5 Θ
Θ heißt charakteristische Temperatur oder DEBYE-Temperatur und hat z. B. für Silber 225 K,
für Eisen den Wert 462 K, und für Diamant 1800 K. Damit lassen sich innere Energie U, Entropie S und in der Folge die Freie Energie F bei tiefen Temperaturen berechnen:
T
T
U = ∫ C v dT ;
0
3.2
3
S=∫
0
Cv
dT ;
T
T
F = − ∫ SdT
(3-5)
0
Gleichgewichtsbedingungen und maximale Arbeit
NERNST erhielt 1920 den Nobelpreis für Chemie in Anerkennung seiner „Arbeiten in der Thermochemie“;
PLANCK war bereits 1918/19 für seine Quantentheorie mit dem NP für Physik ausgezeichnet worden.
14
3.2.1 Gleichgewichtskonstanten
Während ein Prozess (oder eine Reaktion) abläuft, vermindert sich die zur Verfügung stehende
Freie Enthalpie ∆G (Triebkraft)
 ∂g 
 ∂g 
dn

∆G =   = ∑ 
⋅ i = ∑ν i µi
dξ
i  ∂ni  p ,T . n
i
 ∂ξ  p ,T
j
(3-6)
ständig, bis der Gleichgewichtszustand erreicht ist (∆G = 0, bekannt aus Teil I). Dann hat die
Freie Enthalpie bezüglich der Umsatzvariablen (Reaktionslaufzahl) ξ einen Minimalwert erreicht. Infolgedessen ist dort (∂g ∂ξ ) p ,T = 0 und daher auch die Freie Enthalpie ∆G = 0. Die
Mengenanteile der Komponenten nehmen dabei feste Gleichgewichtswerte xG,i an. Die entsprechende, in Mengenanteilen geschriebene Gleichgewichtskonstante ist
K x ( p, T ) = ∏ (xG,i ) i
ν
(3-7).
Sie ist dimensionslos und hängt von p und T ab. Nur noch von T hängt hingegen die in Gleichgewichtspartialdrücken geschriebene Gleichgewichtskonstante Kp ab:
νi
νi
∑ν i

 pG,i 
 p 
p 
K p (T ) = ∏  xG, i Θ  = ∏  Θ  =K x  Θ 
(3-8),
p 

 p 
p 
die - wie aus Teil I bekannt - mit ∆ R G Θ direkt verknüpft ist (vgl. 5-19, Teil I):
∆ R G Θ = ∑ν i µiΘ (T ) = − RT ln K x − RT ∑ν i ln p Θ
p
i
i
(3-9).
νi

p 
Θ
Θ
= − RT ln ∏  xG,i Θ  = − RT ln K p (T ) = ∆ R H − T∆ R S
p 

Entsprechend ist auch die in Gleichgewichtskonzentrationen cG,i = pG, i RT (in der Gasphase)
ausgedrückte Konstante Kc nur von der Temperatur abhängig und kann dimensionslos definiert
werden:
ν
i
 pΘ 
 cG,i 

K c (T ) = ∏  Θ  = K p  Θ
c
RT
c 


∑ν i
∑
 p 
= Kx  Θ

 c RT 
νi
(3-10)
Achtung: p⊝ und c⊝ sind hier nicht thermodynamische Standardbedingungen sondern dienen
der Korrektur der Dimensionen (also jeweils 1 · Dimension).
3.2.2 Systeme im Gleichgewicht
Ein System ist im Gleichgewicht, wenn keine irreversiblen Prozesse mehr ablaufen. Schon im
Teil I hat es sich für die Betrachtung nicht isolierter Systeme als zweckmäßig erwiesen, zwischen einem inneren System (Index i) und einem äußeren System (Index a) zu unterscheiden,
die zusammen ein Gesamtsystem (ohne Index) bilden.
15
In einem isolierten System ist du = dq – pdv = 0, ferner der Wärmeaustausch mit der Umgebung dq = 0 und deshalb auch pdv = 0, d.h. konstantes Volumen. Darüber hinaus ist dq/T = dsa
= 0. Andererseits ist für einen Prozess, also wenn das System noch nicht im Gleichgewicht ist,
ds = dq/T + dsi = 0 + dsi ≥ 0 und deshalb dsi ≥ 0. Damit wird der erste Hauptsatz zu
du = 0 = Tds – Tdsi – pdv ≤ Tds – pdv,
(3-11)
(für isolierte Systeme) wobei sich das Gleichheitszeichen auf den thermodynamischen Gleichgewichtszustand bezieht.
Im Gleichgewicht laufen keine irreversiblen Prozesse mehr ab, d.h. dsi = 0 und auch ds = 0. Da
dsi generell nur positiv sein kann, bedeutet dies, dass im Gleichgewicht die Entropie s einen
Maximalwert und die innere Energie u ein Minimum hat. Letzteres gilt auch für die Enthalpie
wegen dh = Tds – Tdsi + vdp. Natürlich vorkommende Prozesse im isolierten System werden
also immer von einer Entropie-Erhöhung und einer Energie- bzw. Enthalpie-Erniedrigung begleitet. Wie oben gezeigt, treten hier u und h als Funktionen von s und v bzw. s und p auf, was
für Anwendungen auf adiabatische Prozesse praktisch ist, weil dann (im Gleichgewicht) ds =
04 .
Für isotherme Prozesse (geschlossenes System) ist es hingegen zweckmäßiger, die Größen
Freie Energie f (HELMHOLTZ-Energie) und Freie Enthalpie g zu gebrauchen:
f = u – Ts;
g = h – Ts;
df = Tds – Tdsi – pdv – Tds – sdT = – sdT – pdv – Tdsi
dg = Tds – Tdsi + vdp – Tds –sdT = – sdT + vdp – Tdsi
(3-12)
Damit erhält man Gleichgewichtsbedingungen für isotherme, isochore und isobare Systeme, in
denen die Freie Enthalpie g bzw. die Freie Energie f ein Minimum annimmt. Sinnvoll ist die
Verwendung von g für Festkörper oder Flüssigkeiten bei isothermen und isobaren Prozessen,
die Verwendung von f für Gase (in geschlossenem Gefäß) bei isothermen und isochoren Prozessen.
3.2.3 Maximale Nutzarbeit
Bei isothermen Prozessen ist df = – pdv – Tdsi = da – Tdsi ≤ da. Im Fall des reversiblen isothermen Prozesses ist dsi = 0 und df = darev. Die Größe ∆f = – arev bezeichnet daher den Maximalwert der Arbeit, die ein System überhaupt abgeben kann (Maximale Nutzarbeit, engl.
„work function“, „maximum work function“).
Diese maximale Nutzarbeit kann größer sein als du, wenn ds positiv ist wie bei chemischen
Reaktionen, die unter Volumenvergrößerung ablaufen. Ein Beispiel ist die Verbrennung von
Isooctan (2,2,4-Trimethylpentan)
C8H18(gas) + 12,5 O2 → 8 CO2 + 9 H2O (gas).
Bei 298 K und 1 bar ist ∆U = –5108 kJ/mol und ∆S = 0,422 kJ/(mol K), so dass ∆F(298 K) =
(–5109 – 298·0,422 = –5235) kJ/mol.
∆F gibt den Maximalwert der zu erhaltenden Nutzarbeit an. Tatsächlich aber ist bei der
Verbrennung von Isooctan in einer Kalorimeterbombe die Nutzarbeit Null (Volumen konstant).
In einem gängigen Verbrennungsmotor erhält man etwa 1000 kJ/mol und in einer Brennstoffzelle ca. 3000 kJ/mol. Der Gesamtbetrag der Erniedrigung der Freien Energie ist jedoch nicht
4
Man mache sich klar, dass z.B. beim Carnot-Kreisprozess die adiabatischen Teilschritte bei konstanter Entropie
ablaufen.
16
in praktischer Weise aus der Benzinverbrennung zu erhalten, da hierbei 1. alle Reibungsverluste in Getrieben usw. ausgeschaltet werden müssten und 2. die Verbrennung unendlich langsam
zu erfolgen hätte (reversibler Prozess).
3.2.4 Zusammenhang zwischen thermodynamischen Potenzialen
Die zum Teil bereits mehrfach verwendeten und für reversible Prozesse geltenden (wegen dsi =
0) Beziehungen (3-13) bis 3-16)
du = Tds – pdv = (∂u/∂s)v ds + (∂u/∂v)s dv
dh = Tds + vdp = (∂h/∂s)v ds + (∂h/∂p)s dp
df = –sdT– pdv = (∂f/∂T)v dT + (∂f/∂v)T dv
dg = –sdT + vdp = (∂g/∂T)p dT + (∂g/∂p)T dp
(3-13)
(3-14)
(3-15)
(3-16)
kann man sich entweder jeweils klarmachen oder ihre Aufstellung mit Hilfe eines Merkschemas vornehmen:
+ –
s u v
h
f
p g T
Hierzu ein Merkvers:
schöne und vornehme frauen Tragen große prächtige
hüte
Das Prinzip des Merkschemas ist, dass die Energiegrößen jeweils zwischen den Variablen stehen (mit Vorzeichen), von denen sie abhängen, und die dann noch mit den diagonal dazu stehenden Größen zu multiplizieren sind, z.B. du = + Tds –pdv (wie 3-13).
Alle thermodynamischen Potenziale sind Zustandsfunktionen, so dass die gemischten 2. Ableitungen gleich sind (MAXWELLsche Beziehungen):
 ∂T 
 ∂p 
Für u nach (3-13):   = −  ,
 ∂v  s
 ∂s  v
 ∂T   ∂v 
für h nach (3-14):   =   ,
 ∂p  s  ∂s  p
 ∂s 
 ∂p 
für f nach (3-15):   =   ,
 ∂v  T  ∂T  v
 ∂s 
 ∂v 
für g nach (3-16):   = −  .
 ∂T  p
 ∂p  T
Für solche Beziehungen gibt es zahlreiche Anwendungen, etwa die Beschreibung des JOULETHOMSON-Effekts bzw. -Koeffizienten (s. oben und Lehrbücher). Entsprechend ergeben sich
die in den Ecken des Merkschemas stehenden Größen als partielle Ableitung des jeweils schräg
gegenüberstehenden thermodynamischen Potenzials nach der diagonal gegenüberstehenden
Größe:
 ∂u 
 ∂h 
 ∂f 
 ∂g 
T =   =   ; s = −   = − 
 ∂s  v  ∂s  p
 ∂T  v
 ∂T  p
vgl. 3-13 bis 3-16 (s. auch 3-44, 3-45 in Teil I).
 ∂h   ∂g 
 ∂u 
 ∂f 
p = −  = −  ; v =   =  
 ∂v  s
 ∂v  T
 ∂p  s  ∂p  T
17
3.3
Mischphasen
3.3.1 Partielle molare Größen
Die Erfahrung zeigt, dass extensive Zustandsgrößen nicht immer additiv sind. Z.B. machen ca.
20-%-ige Schnäpse immer einen öligen Eindruck. Hier liegt ein Dichtemaximum für Mischungen aus Ethanol und Wasser vor. Deren Mischungen weisen in diesem Zusammensetzungsbereich immer ein Volumen auf, das kleiner ist als die Summe der Einzelvolumina. Es ist daher
zweckmäßig, partielle molare Größen zu definieren, etwa
 ∂v 

Vi = 
(3-17)
∂
n
 i  p ,T , n
j
Partielle Volumina können sogar negativ (MgSO4 in Wasser) oder Null (Eier im Eierkarton)
sein.
Hält man die Zusammensetzung konstant, so folgt wegen der Extensivität von v aus
dv = Σ Vi dn i
(3-18),
v = Σ Vi n i
(3-19).
dass
Bildet man das Differential, so ergibt sich jedoch dv = ΣVi dni + Σni dVi. Das kann nur richtig
sein, wenn
Σ n i dVi = 0
(3-20)
(vgl. GIBBS-DUHEM-Gleichung, Anhang 2). Hieraus folgt, dass die partiellen Volumina nicht
alle unabhängig voneinander sind: Im binären System (Zweistoff-System) ist
n 1 dV1 = –n 2 dV2
(3-21).
Zur experimentellen Bestimmung von Partialvolumina kann allgemein die Definitionsgleichung (3-17) dienen. Für binäre Mischungen existiert eine genauere Methode, die von dem
mittleren Molvolumen
V =
v
= x1V1 + x 2V 2 = (1 − x 2 )V1 + x 2V 2
n1 + n 2
(3-22)
ausgeht, woraus folgt, dass
 ∂v 
 ∂V 
 = V + (n1 + n 2 )

V1 = 
 ∂n1  n2
 ∂n1  n2
(3-23).
Da
 ∂V  dV

 =
∂
n
 1  dx 2
 ∂x 2 
dV

 =
 ∂n1  n2 dx 2
erhält man aus (3-23)

n2
−
 (n + n ) 2
1
2





(3-24),
18
dV
dx 2
das ist die Gleichung einer Geraden.
V1 = V − x 2
(3-25),
Bestimmt man also das mittlere Molvolumen als
Funktion von x2, so erhält man die Partialmolvolumina als Achsenabschnitte einer Tangente an die Kurve
(s. Skizze).
3.3.2 Mischungsentropie
Das chemische Potenzial eines reinen (Index 0) idealen Gases ist gegeben durch
p
(3-26),
pΘ
wobei sich µiσ hier auf einen Normaldruck bzw. Standarddruck (1 bar oder 1 atm) bezieht (zum
ln-Term vergl.Teil I, Gl. (5-12)).
In einer Mischung von idealen Gasen sind die Mengenanteile xi der Komponenten mit dem
Partialdrücken pi und dem Gesamtdruck p durch pi = xi p ((2-5) in Teil I) verknüpft, und das
chemische Potenzial der Komponente i in der Mischung ist
µ 0i = µiΘ (T ) + RT ln
µ i ( p, T , x i ) = µ iΘ (T ) + RT ln
pi
= µ 0i ( p, T ) + RT ln x i
pΘ
(3-27)
Für xi = 1 ergibt sich das chemische Potenzial des reinen Stoffs. Bei sich nicht ideal verhaltenden Gasen führt man die Aktivität ai ein (vgl. Teil I, Kap. 5.2). Sie bezeichnet einen um die
Abweichung von der Idealität korrigierten Stoffmengenanteil: ai = ϕi · xi (ϕi : Aktivitäts- oder
Fugazitätskoeffizient5). Damit wird
µ i = µ 0i + RT ln ai
(3-28)
(Erinnerung: So definiert ist die Aktivität dimensionslos und ohne Trick zu logarithmieren.)
Entfernt man in einem System mit zunächst getrennten Gasen A und B die Trennwand, so tritt
spontane Durchmischung ein, verbunden mit einer Erhöhung der Entropie und einer Erniedrigung der Freien Enthalpie. Es gilt im System mit getrennten Gasen g0 = nA µ 0A + nBµ 0B und
nach der Durchmischung gm = nA µ A + nBµ B. Entsprechend ist die Freie Mischungsenthalpie
∆g m = g m − g 0 = n A ( µ A − µ 0 A ) + n B ( µ B − µ 0 B )
= n A RT ln x A + n B RT ln x B = (n A + n B ) RT ( x A ln x A + x B ln x B )
(3-29)
Wegen 0 ≤ xi ≤ 1 ist ∆gm < 0.
Allgemein lässt sich der Effekt der Mischung von idealen Gasen auf den Zahlenwert der Freien
Enthalpie wie folgt ausdrücken
5
In diesem Text wird unterschieden fi: Aktivitätskoeffizient bei kondensierten Mischungen, ϕi: Fugazitäts- oder
Aktivitätskoeffizient bei Gasen (Dämpfen); γi: Ionenaktivitätskoeffizient; Aktivitäten immer a1.
19
∆g m = (∑ ni )RT ∑ xi ln xi
(3-30)
Daraus folgt für die Mischungsentropie
 ∂∆g m 
(3-31)
∆sm = −
 = − (∑ ni )R ∑ xi ln xi > 0
 ∂T  p , ni
Für binäre Mischungen (idealer Gase) durchlaufen ∆gm ein Minimum und T∆sm ein Maximum
als Funktion von x, jeweils bei xi = 0,5. ihre Summe ist jeweils = 0. Deshalb verschwindet die
Mischungsenthalpie ∆hm für ideale Mischungen:
∆hm = ∆gm + T∆sm = 0
(3-32),
im realen Fall erhält man jedoch
∆gm = (Σni) RT Σxi ln ai = (Σni) RT Σxi ln ϕixi
(3-33).
Die Differenzen zwischen diesen Größen und denen für die idealen Systeme werden als Exzess-(Zusatz-, Überschuss-)Größen bezeichnet; z.B. ist die Freie Exzess-Enthalpie
∆gE = ∆gm – id∆gm = (Σni) RT Σxi ln ϕi
(3-34).
Die Exzess-Enthalpie ist identisch mit der experimentell bestimmbaren Mischungsenthalpie
(Mischungs- bzw. ggf. Lösungswärme)
 ∂∆g E 
∆hE = ∆g E + T∆sE = ∆g E − T 

 ∂T  p , ni
 ∂ ln ϕ i 
= − (∑ ni )RT 2 ∑ xi 

 ∂T  p , ni
(3-35).
= ∆g m + T∆sm = ∆hm
3.4 Grenzflächen
In belebten Natur und in der modernen synthetischen Chemie sowohl im Forschungslabor als
auch in der technischen Umsetzung laufen die meisten Reaktionen an Grenzflächen ab (Membranen, Katalysatoren). Kenntnisse über die Thermodynamik von Adsorption und Desorption,
Benetzung, Schichtbildung, Keimbildung, usw. sind deshalb in Verbindung mit der zugehörigen Kinetik und Analytik unverzichtbares Rüstzeug eines Chemikers.
An der Grenzfläche zwischen zwei Phasen unterliegen die Moleküle einseitigen Anziehungskräften und haben daher eine andere Energie als die Moleküle innerhalb der Phase. Bei
makroskopischen Körpern ist die Zahl der Grenzflächenmoleküle klein gegenüber der Gesamtzahl der Moleküle des Körpers und man kann die Energieunterschiede meist vernachlässigen.
Oberfläche O und Volumen stehen jedoch nicht in einem festen Verhältnis. Wird bei konstanter Gesamtmasse der Körper immer mehr zerkleinert, so vergrößert sich die Oberfläche gewaltig. Beispiel: Ein kubischer Kristall mit 1 cm Kantenlänge bestehe aus Atomen von 0,2 nm
20
Durchmesser; entlang einer Kante befinden sich 5·107 Atome, insgesamt sind 125·1021 Atome
im System. An der Oberfläche befinden sich dann 6·(5·107)2 = 1,5·1016 Atome entsprechend
1,2·10-5 % der Gesamtzahl. Zerkleinert man den Kristall in Würfelchen von 0,1 µm = 10-5 cm
Kantenlänge, so ist die Zahl der Atome an der Oberfläche aller 1015 Kristallite nunmehr 6·5002
1015 = 1,5·1021 entsprechend 1,2 %.
3.4.1 Thermodynamische Größen der Grenzflächenchemie
3.4.1.1 Einkomponentensysteme (Oberflächenspannung und Keimbildung)
Das Zerkleinern eines solchen Kristalls erfordert die Zufuhr von mechanischer Arbeit. Allgemein wird die Energie eines Systems erhöht, wenn die Oberfläche um den Betrag dO vergrößert wird, so dass man schreiben muss
dg = vdp − sdT + γdO
dh = Tds + vdp + γ dO
du = Tds – pdv + γ dO
df = –sdT – pdv + γ dO
(3-36)
Die Größe
 ∂g 
 ∂u 
 ∂h 
 ∂f 
 =
 =
 =

 ∂O  p ,T  ∂O  s ,v  ∂O  s , p  ∂O  T ,v
γ =
(3-37)
heißt Oberflächenspannung oder Oberflächenarbeit und ist immer positiv. Sie wird in J/cm2
oder mN/m (Milli-Newton pro Meter)angegeben.
K
dx
l
Dass die Oberflächenarbeit ein reversibler Arbeitsbetrag ist, ergibt sich
aus dem Bügelversuch. Um eine Flüssigkeitslamelle im Gleichgewicht
zu halten, muss eine Kraft K aufgewendet werden. Zur Verschiebung des
Bügels um eine Strecke dx muss die reversible Arbeit
da = Kdx = γdO = γ·2·ldx
(3-38)
aufgewendet werden, d.h.
γ = K / (2 l).
(3-39)
Für die nachfolgende Betrachtung, bei der p und v konstant gehalten werden, ist es zweckmäßig, die Freie Energie f = u – Ts (auch Helmholtzenergie genannt) zu verwenden.
Gleichzeitige Änderung von Volumen und Oberfläche
Wird ein Dampf kondensiert (Tröpfchenbildung) bzw. in ein Gefäß mit gekrümmten Grenzflächen (Kapillarsystem) einkondensiert, so treten Oberflächen und Volumenänderungen gleichzeitig auf. Hierzu das skizzierte Gedankenexperiment: Zufuhr
der Arbeit da durch Bewegung des Kolbens im linken Zylinder
nach rechts bewirkt eine reversible Änderung der Oberfläche
und der beiden Volumina vg und vfl, dann ist
da= – pfldvfl – pgdvg + γdO
(3-40).
Aus dem ersten Hauptsatz du = dq + da und der Definition der Freien Energie f erhält man
21
df = – sdT – pfldvfl – pgdvg + γdO
(3-41).
(und entsprechende Beziehungen für dh und dg).
Im Gleichgewicht fl ⇌ g hat die Freie Energie ein Minimum und bei konstanter Temperatur ist
df = 0 = – pfldvfl – pgdvg + γdO
(3-42).
Bei konstantem Gesamtvolumen ist dvg = – dvfl und daher
(pfl –pg)dvfl = γdO
(3-43).
Bei Flüssigkeiten mit ebenen Oberflächen, die sich in zylindrischen Gefäßen befinden, bewirkt
eine Ausdehnung dvfl der flüssigen Phase auf Kosten der Gasphase keine Veränderung der Oberfläche O; d.h. dO = 0 und daher ist auch pfl = pg.
Ist jedoch die Flüssigkeit ein kugelförmiges Tröpfchen vom Radius r, so gilt dvfl = 4πr2dr und
dO = 8πrdr, so dass
pfl − pg = γ
dO 2γ
=
r
dvfl
(3-44),
d.h. der Druck im Tropfen ist größer als in der Gasphase und der kleine Tropfen ist nur existent, weil die Oberflächenspannung wie eine Membran um den Tropfen wirkt.
Für den Stoffaustausch zwischen den Phasen (Verdampfung bzw. Kondensation) gilt im
Gleichgewicht µfl = µg und dµfl = dµg . Wegen
dµ = − SdT + Vdp
(3-45)
ist bei konstanter Temperatur
Vfl dpfl = Vg dpg
(3-46)
und aus (3-44)) folgt
 Vg

1
d( pfl − pg ) =  − 1dpg = 2γd 
(3-47)
r
 Vfl

Da Vg >> Vfl, kann Vg bei Gültigkeit des idealen Gasgesetzes ersetzt werden:
RT
 1  Vg
2γd   =
dp g =
dp g
Vfl pg
 r  Vfl
(3-48).
Integration von p0 (Dampfdruck bei ebener Oberfläche, d.h. 1/r → 0) bis p ergibt
2γ RT
p
=
ln
r
Vfl
p0
bzw.
ln
p 2γ Vfl
=
⋅
p0
r RT
(3-49)
22
d.h. der Dampfdruck p eines kleinen Tröpfchens ist größer als der über einer ebenen Flüssigkeitsoberfläche und sehr kleine Tröpfchen sind unstabil (s. u.). Ähnliches gilt für die Kristallisation/Löslichkeit kleiner Festkörperteilchen.
Keimbildung
Die Bildung einer neuen Phase, z.B. beim Kristallisieren von Festkörpern aus Flüssigkeiten,
Kondensieren von Flüssigkeiten aus Dämpfen usw., verläuft über kleine Molekülaggregate
(„Keime“). Erfahrungsgemäß findet Keimbildung nur statt, wenn eine gewisse Übersättigung
vorliegt. Sehr reines Wasser kann z.B. ohne weiteres auf –40 °C unterkühlt werden, bevor
spontane Kristallisation einsetzt. Die Ursache für dieses Verhalten ist die geringe Stabilität der
kleinen Molekülaggregate.
Die Aggregation von Molekülen eines übersättigten Dampfes D zu einem Keim K
(Flüssigkeitströpfchen) D ⇌ K ist mit einer Änderung der Freien Enthalpie verbunden, die sich
bei konstanter Temperatur durch
dg = v dpD + (vK dpK ) + γdO
(3-50)
ausdrücken lässt, wobei vD und vK die Volumina von Dampf und Keim bezeichnen und vK gegenüber v vernachlässigt werden kann. Entsprechend sind pD und pK die (im allgemeinen verschiedenen) Drücke im Dampf und im Keim. O ist die Oberfläche des Keims und γ die Oberflächenspannung. Wenn sich der Dampf ideal verhält, und wenn der Keim die Form eines kugelförmigen Tröpfchens vom Radius r hat, gilt für die Kondensation von n Mol Dampf
p
∆g = − n RT ln D + 4 πr 2γ
(3-51),
pK
wobei der zweite Term in (3-81) wegen vK << vD vernachlässigt wurde. Drückt man n durch
das Molvolumen VK der Keimphase aus, so wird
4 πr 3
p
∆g = −
RT ln D + 4 πr 2γ
(3-52)
3 VK
pK
=n
Im Fall der Übersättigung ist pD > pk und ∆g(r) durchläuft ein Maximum, das zu einem kritischen Tröpfchenradius rc gehört, und zwar erhält man aus (3-63) für d∆g = 0 die Beziehung
rc =
mit
2γ VK
RT ln( pD / pK )
(3-53)
4 2
π rc γ
3
(3-54).
∆g max =
Das Maximum in der Kurve ∆g = f(r) folgt auch, wenn man die Gibbs-Helmholtz-Gleichung
∆g = ∆h – T ∆s + γ∆O (mit Berücksichtigung der Oberflächenänderung) ansetzt. ∆O ist zu Beginn der Kondensation so groß, dass ∆g positiv ist; wird dann bei wachsendem r kleiner und
verschwindet schließlich bei sehr großen r entsprechend einer (praktisch) ebenen Grenzfläche.
Die Kurve schwenkt dann in einen negativen konstanten ∆g-Wert für die Kondensation ein.
23
Beispielsweise wird für Wasserdampf von 0 °C und pD/pK = 4 mit Hilfe von (3-53) ein kritischer Wert rc = 0.83 nm berechnet, der einem Keim von 90 Wassermolekülen entspricht.
Für r < 3rc/2 ergibt sich aus (3-54) mit (3-53) dass ∆g > 0. Keime dieser Größe sind daher
nicht stabil und können unter Erniedrigung der Freien Enthalpie wieder zerfallen; an größeren
Keimen, für die < 0 ist (d.h. r > r0 = 3rc/2), verläuft die Kondensation dagegen spontan, bis ein
Gleichgewichtszustand erreicht ist. Setzt man (3-53) in (3-54) ein
16π γ 3 V 2
∆g max =
(3-55),
3 [ RT ln( pD / pK )]2
so ergibt sich, dass ∆gmax durch Erhöhung der Übersättigung pD/pK herabgesetzt werden kann.
Damit erhöht sich auch die Geschwindigkeit der Keimbildung, die insbesondere von der thermischen Wahrscheinlichkeit der kritischen Keime abhängt (und mit der statistischen Theorie6
von Becker und Döring berechnet werden kann; Ann. Phys. 24 (1935) 719; s. auch Bradley,
Quart.Rev. 5 (1951) 315).
3.4.1.2 Mehrkomponentensysteme (GIBBS-Adsorptionsisotherme)
Bei jedem Zweiphasensystem kann man drei Bereiche unterscheiden: zwei homogene Phasen
α und β und eine Zwischenphase, in der die Eigenschaften der einen Phase kontinuierlich in
die der anderen übergehen. Um die Eigenschaften der Zwischenphase genau zu beschreiben,
müsste ihre Zusammensetzung bekannt sein.
Im Allgemeinen hängen die Konzentrationen der
Komponenten in der Zwischenphase empfindlich
von der Lage der Begrenzungen der Zwischenphase gegenüber den beiden homogenen Phasen
ab. Da es unmöglich ist, diese Begrenzungen mit
der erforderlichen Genauigkeit (Bruchteile von
nm) festzulegen, geht man in der Thermodynamik
von einem phänomenologischen Modell aus, nach dem eine streng 2-dimensionale Fläche das
gesamte Volumen in zwei Anteile unterteilt:
v = vα + vβ
(3-58)
Für jede Komponente i definiert man Mengen
nαi = cαi vα ;
nβi = cβi vβ
(3-59)
durch die Konzentrationen cαi und cβi im Inneren der homogenen Phasen α und ß. Damit das
Modellsystem mit dem realen übereinstimmt, muss die Gesamtmenge der Komponente i durch
ni = nαi + nβi + nOi
(3-60)
gegeben sein, wobei nOi eine Überschussgröße bezeichnet, die der Fläche O zugeordnet ist. Je
nachdem, ob in der Zwischenphase eine Anreicherung oder Verarmung der betreffenden Komponente stattfindet, ist nOi positiv oder negativ (seltener = 0).
Davon abgeleitet ist die Oberflächenkonzentration (auch„Adsorption“ genannt)
Γ i = nOi / O (in mol/cm2)
(3-61)
die ebenfalls eine Überschussgröße bezeichnet.
Analog definiert man Oberflächenenergie, -entropie, usw. durch
6
Siehe Anhang 2
24
uO = u − uα − u β
;
uβ = U β vβ
usw.
sO = s − sα − s β
usw.; daher folgt für dp = 0
dgO = − sO dT + γdO + ∑ µi dnOi
(Im Gleichgewicht ist µ Oi = µ αi = µ βi = µ i). Bei konstanter Temperatur ist
dg O = γ dO + ∑ µ i dnOi
und
g O = γO + ∑ µi nOi
Differentialbildung führt zu
dgO = γ dO + O dγ + ∑ µ i dnOi + ∑ nOi dµ i
bzw. (analog zur GIBBS-DUHEM-Gleichung7)
O dγ + ∑ nOi dµi = 0 = O dγ + ∑ O Γ i dµi
Dividiert man durch O, so wird
dγ = − ∑ Γ i dµ i
GIBBSsche Adsorptionsgleichung
(3-62)
(3-63)
(3-64)
(3-65)
(3-66)
(3-67)
(3-67)
(3-69)
bzw. für zwei Komponenten
dγ = − Γ 1 dµ1 − Γ 2 dµ 2
(3-70).
Wegen der Gibbs-Duhem-Gleichung
∑
ni dµ i = 0
(3-71)
können µ 1 und µ 2 nicht unabhängig voneinander variiert werden ( dµ1n1 = −dµ2 n2 ). Man
schreibt daher
dµ1 = −dµ2 n2 / n1 ≈ −dµ2 c2 / c1
(3-72),
so dass nach (3-70)

c 
dγ = − Γ 2 − Γ 1 2  dµ 2
c1 

(3-73)
Der Ausdruck
Γ 2,1 = Γ 2 − Γ 1
 ∂γ 
c2

= −
c1
 ∂µ 2  T
(3-74)
bezeichnet daher eine relative Oberflächenkonzentration. Für ideale Lösungen gilt
µ 2 = µ 2o + RT ln c2 / c Θ
(3-75)
und man kann relative Oberflächenkonzentrationen aus der Konzentrationsabhängigkeit der
Oberflächenspannung bestimmen nach
Γ 2,1 = −
7
Siehe Anhang 3
1
RT


∂γ


o 
∂
ln
c
/
c
2

T
(3-76).
25
Es folgt unmittelbar, dass Substanzen, die die Oberflächenspannung herabsetzen (oberflächenaktive Substanzen) in der Grenzschicht angereichert sind (Γ2,1 > 0). In praktischen Fällen ist
die Komponente 1 das Lösemittel und die Komponente 2 ein gelöster Stoff, z.B. ein Spülmittel
(Tensid) in Wasser. Die Phasengrenzfläche zwischen Lösung und Luft ist in guter Näherung so
zu definieren, dass sich für Wasser keine Überschusskonzentration ergibt. Dann ist Γ1 = 0 und
Γ2,1 = Γ2.
Gl. (3-69) ist eine rein thermodynamische Beziehung und gilt daher streng. Dennoch ist eine
Überprüfung reizvoll, und die dazu angestellten Experimente haben wesentlich zum Verständnis der Anreicherung von oberflächenaktiven Substanzen in Grenzschichten beigetragen. Drei
brauchbare Methoden:
– Abscheren von Grenzschichten mit Mikrotomen und Analyse
– Ellipsometrie (Änderung des Polarisationszustands von Licht bei Refexion oder Transmission)
– Verwendung von Substanzen, die mit Atomen wie 14C, 35S usw. markiert sind, deren weiche β-Strahlung eine Reichweite von der Größenordnung der Grenzschichtdicke hat, z.B.
3.4.2 Adhäsion und Kohäsion von Flüssigkeiten, Spreitprozesse
Ein quantitatives Maß für die Adhäsion einer Flüssigkeit B an
einer Flüssigkeit A ist die Oberflächenarbeit ∆aBA, die verrichtet
werden muss, um die Flüssigkeiten von einander zu trennen. Dabei entstehen zwei neue, gleich große Oberflächen ∆O der Flüssigkeiten gegen Luft:
∆a BA = (γ A + γ B − γ BA ) ∆O
(3-77)
(∆aBA ist die Adhäsionsarbeit, γ jeweils gegen Luft gemessen)
Ist B = A, so erhält man wegen γ AA = 0 die Kohäsionsarbeit:
∆a AA = 2γ A ∆O
(3-78),
die bei der Trennung eines Flüssigkeitsvolumens in zwei Teile aufzubringen ist.
Beim Spreiten von B auf A findet eine spontane Ausbreitung eines
zunächst aufgebrachten dicken Tropfens statt. Bei konstanten Werten
von Druck und Temperatur gilt für die mit dem Spreiten verbundene
Änderung der Freien Enthalpie des Gesamtsystems
dg = γ A dOA + γ B dOB + γ BA dOBA
(3-79).
Da sich die Oberfläche von B gegenüber Luft und gegenüber A auf Kosten der Oberfläche von
A (gegenüber Luft) vergrößert, gilt
dOB = dOBA = −dOA = dO
und
(3-80)
26
− ∆g = (γ A − γ B − γ BA ) ∆O = SBA ∆O
(s. A. W. Adamson, Physical Chemistry of Surfaces, Kap. IV).
(3-81)
Der Spreitungskoeffizient SBA ist daher positiv, wenn Spreiten spontan erfolgt. In diesem Fall
ist die Adhäsion von B und A größer als die Kohäsion von B:
SBA = (∆aBA – ∆aBB)/∆O
(3-82)
Die Spreitung unterscheidet sich prinzipiell von der Anreicherung einer oberflächenaktiven
Substanz in der Grenzfläche (siehe oben), weil sich B in der unteren Phase A nicht löst oder
nur in einer sehr kleinen aber konstanten Konzentration vorliegt. Wenn sich B und A etwas
ineinander lösen, ist im allgemeinen SB(A)A(B) ≠ SBA. So findet man, dass Benzol auf Wasser zunächst spreitet, weil SBA > 0; anschließend zieht sich das aufgetropfte Benzol zu einer Linse an
der Wasseroberfläche zusammen, weil SB(A)A(B) < 0.
3.4.2.1 Monoschichten
Die Spreitung tritt bei schwer löslichen Substanzen auf, die einen dünnen Film auf der Oberfläche einer Flüssigkeit (oder einer anderen Unterphase) bilden. Die Oberflächenkonzentration
ist hier unmittelbar durch die auf die Flächeneinheit aufgegebene Substanzmenge definiert und
daher nicht besonders interessant. Wichtiger ist die Herabsetzung der Oberflächenspannung
durch die bedeckende Schicht, die bei Destillationsvorgängen,
bei der Flotation und bei Waschprozessen (Verhinderung der
Schaumbildung!) eine praktische Rolle spielt. Auch die Bildung
eines Flüssigkeitsfilms auf Schleimhäuten gehört hierher.
Typischer Vertreter dieser Substanzklassen sind die höheren
Fettsäuren und -alkohole, die sich über eine beliebig große Wasseroberfläche spontan ausbreiten („Spreiten“, s.o.), aber auch
durch bewegliche Barrieren zusammengeschoben werden können. Es hat sich gezeigt, dass
sich die Oberflächenspannung solcher Schichten drastisch ändert, wenn der Substanz weniger
als etwa 0.2 nm2/Molekül zur Verfügung steht („POCKELS-Punkt8“). Dieser Wert wird als
Platzbedarf eines Moleküls in einem monomolekularen Film gedeutet. Da der Platzbedarf unabhängig von der Kettenlänge ist (zwischen C16 und C26 geprüft), ergibt sich, dass die Fettsäuremoleküle am POCKELS-Punkt senkrecht zur Oberfläche angeordnet sein müssen.
Die beim Spreiten auftretenden Kräfte lassen sich in einem LANGMUIR-Trog messen: der Trog
wird zunächst bis zum Rand mit reinem Lösungsmittel (meist Wasser) gefüllt. Zwischen Barriere und Schwimmer wird ein Tropfen einer Lösung aufgetragen, die den Schichtbildner enthält (z.B. Stearinsäure in Benzol). Nach dem
Verdunsten des Lösemittels kann man die Eigenschaften der Schicht durch Verschieben der
Barriere und Messen der dabei am Schwimmer
auftretenden Kräfte untersuchen.
Als Oberflächendruck bezeichnet man die Größe
π = γ0 −γ
(3-83),
wobei γ0 und γ die Oberflächenspannung von reiner Unterphase und von der Unterphase mit gespreiteter Schicht bezeichnen. Die Verschiebung
8
Nach AGNES POCKELS, 1862-1935, Braunschweig
27
des Schwimmers erfordert einen Arbeitsbetrag ( da = −π ⋅ l ⋅ dx = −π ⋅ dO ).
Trägt man π gegen O bei verschiedenen Temperaturen auf, so erhält man Isothermen, die für
verschiedene Substanzen sehr unterschiedlich sein können. Wenn die Wechselwirkung zwischen den Molekülen gering ist (oder die Verdünnung hinreichend hoch), verhält sich die Substanz wie ein zweidimensionales Gas:
RT
πO = nO RT = mO
(3-84) bzw.
M
π = Γ RT
(3-85)
Bei zunehmender Oberflächenkonzentration verhalten sich die Substanzen wie ein zweidimensionales VAN-DER-WAALS-Gas. Die Analogien werden nachfolgend verdeutlicht:
ideales Gas
n RT
p=
v
[Hyperbel p= f(v)]
RT
M
Aus kinetischer Gastheorie:
pv = nRT = m
2
↓
1
2
↓
1
L m w2
3
L: Loschmidtzahl
2
( RT = ) pV = L ⋅ ε kin
3
(εkin) = kinetische Energie
= Translationsenergie εt
pv =
gespreitete Moleküle (ideal)
n ⋅ RT
π= O
= Γ ⋅ RT [Hyperbel π = f(O)]
O
RT
π ⋅ O = nO ⋅ RT = mO
M
3
3
2
2
3 Freiheitsgrade
ε t = RT / L = kT
1
N O m w2
2
NO = Teilchenzahl / Fläche
für 1 Teilchen:
1
kT = π ⋅ σ = m w 2 = ε kin = ε t
2
σ : Fläche, die ein Molekül beansprucht
π=
εt = kT
2 Freiheitsgrade
reales Gas:
a 

 p + 2 (V − b) = RT
V 

gespreitete Schicht (real):

α 
 π + 2 (σ − β ) = k ⋅ T
FM 

„VAN-DER-WAALS-Gleichung“
FM: Flächenbedarf eines Moleküls (bzw.
seiner Kopfgruppe)
28
(schwer zu messen, Barriere sehr langsam bewegen!)
I = gasanalog, II = Koexistenz gasanalog / flüssiganalog (Filmbildung),
III = flüssig-ausgedehnt, IV = Koexistenz flüssigausgedehnt / flüssig-kondensiert
(Folie)
V = flüssig-kondensiert, VI = fest-kondensiert, VII
= kollabierte Phase
Monoschichten behindern die Verdampfung der Flüssigkeit, die sie bedecken. Sie setzen dem
Übertritt der Flüssigkeitsmoleküle in die Gasphase einen vom Oberflächendruck π abhängigen Widerstand entgegen. Bei Vergrößerung des Oberflächendrucks geht der Widerstand
gegen einen konstanten Grenzwert, der der dicht gepackten fest-kondensierten Phase entspricht und deshalb die Ermittlung des Platzbedarfs der Kopfgruppe bzw. des Molekülquerschnitts ermöglicht. Von besonderem Interesse sind reaktionskinetische Studien an Monoschichten, da hier die Möglichkeit besteht, Moleküle in bestimmter Orientierung zueinander
reagieren zu lassen.
3.4.3 Benetzung
Wenn sich ein Flüssigkeitstropfen L in der Atmosphäre eines Gases G auf der festen Unterlage S befindet,
dann treten die drei Grenzflächenspannungen γGS, γGL,
und γLS auf, und es bildet sich ein für die Benetzung
der Oberfläche charakteristischer Randwinkel θ aus. Im Gleichgewicht ist
28
29
γ GS = γ LS + γ GL ⋅ cos θ
(YOUNG-Gleichung)
(3-86).
γGS und γLS sind nicht unabhängig voneinander meßbar; ihre Differenz ist die Haftspannung
γH= γGS – γLS, die positive und negative Werte annehmen kann. Für θ < 90° ist γH > 0.
Dagegen ist γH < 0, wenn 90° < θ < 180 °.
Im ersteren Fall spricht man davon, dass die
Flüssigkeit den Festkörper benetzt (z.B.
Wasser an Glas), im letzteren, dass sie ihn
nicht benetzt (z.B. Wasser auf Paraffin oder
Quecksilber auf Glas).
Proportional zur Haftspannung ist die Steighöhe h von Flüssigkeiten in Kapillaren Ist r
der Radius der Kapillare, so kann man näherungsweise9 die Oberfläche des Flüssigkeitsspiegels in der Kapillare als Teil einer Kugeloberfläche mit demselben Radius auffassen. Im
Gleichgewicht halten sich der hydrostatische Druck ρgh der Flüssigkeitssäule und der durch
2γ
(3-44) gegebene Kapillardruck pfl − pg =
die Waage:
r
2γ H
2γ cos θ
h=
= GL
(3-87)
ρ gr
ρ gr
(ρ ist die Dichte der Flüssigkeit und g die Erdbeschleunigung). Bei benetzenden Flüssigkeiten (θ ≈ 0) ist die Bestimmung der Steighöhe eine bequeme Methode zur Messung von Oberflächenspannungen γGL. Komplizierte Apparaturen ermöglichen die Bestimmung des Kontaktwinkels θ.
Temperaturabhängigkeit der Oberflächenspannung γ
Als Funktion der Temperatur muss die Oberflächenspannung beim kritischen Punkt verschwinden. Empirisch gilt im linearen Teil untenstehender Skizze bis zu Temperaturen, die
nur wenig unter der kritischen Temperatur Tk liegen, die EÖTVÖS-Regel
2
γVfl 3 = k E (Tk − 6K - T )
(3-88),
wobei kE als EÖTVÖS-Konstante bezeichnet wird. Etwa 6 K
unterhalb von Tk geht der lineare Abfall der Kurve in einen
gekrümmten über (s. Abb..
Nach dem Theorem der übereinstimmenden Zustände (s.
Kap. 1.1.2) sollte kE eine universelle Konstante vom Betrag
ca. 230 nJ·K–1 mol–2/3 sein. Praktisch findet man jedoch nur bei einigen unpolaren Substanzen übereinstimmende kE-Werte, die sich sonst als sehr individuell erweisen (s. Tabelle).
9
Siehe Anhang 1
29
30
-6 3
γ/ mJ/m2 Vfl /10 m /mol
Substanz
T /°C
He
–270.7
0.308
32.792
77.9
N2
–200
9.85
17.34
152.4
H2O
20
72.75
18.016
101.7
CCl4
20
26.95
96.499
254.8 ←
C2H5OH
20
22.75
58.368
129.4
CH3COCH3
20
23.70
73.528
220.3 ←
C6H6
20
28.85
88.909
265
←
Hg
25
483.5
14.808
204
←
Na
110
205.7
24.496
Ag
1100
907
11.763
 d  γV 2 3 

  fl 

nJ
= kE  /
−
2
dT

 Kmol 3


42.5
160
4. Kinetik
4.1 Bimolekulare Reaktionen
Gasphase
Ganz allgemein lässt sich die Geschwindigkeit einer Reaktion mit Hilfe der im Teil I bereits definierten Reaktionslaufzahl10 ξ (dξ = dni/νi) als Umsatzgeschwindigkeit ω
ω = dξ / dt
(4-1)
formulieren. Die Reaktionsgeschwindigkeit r ist dann
r = ω / v = (1/νi)(dci /dt);
(4-2),
wobei die νi stöchiometrische Koeffizienten der Reaktionsgleichung (mit Vorzeichen) angeben. r wird für bimolekulare Reaktionen meist in mol dm3 s-1 oder in (bar s)-1 angegeben, oft
auch einfach reziproken Teilchendichten: cm3 s-1. Falls sich das Volumen bei der Reaktion
nicht ändert, sind Umsatzgeschwindigkeit und Reaktionsgeschwindigkeit proportional zueinander.
Einfachster Typ einer bimolekularen chemischen Elementarreaktion ist A + B → P (P:
allgemein Produkte). Nach diesem Schema laufen viele Atom- und Radikalreaktionen in der
Gasphase ab, wie z.B. Na + Cl2 → NaCl + Cl. Die Wahrscheinlichkeit der Bildung von Pro-
10
dξ = 1 mol bedeutet, dass ein Formelumsatz durchlaufen wurde
30