1 Stoffgleichgewicht (Materiegleichgewicht) Die

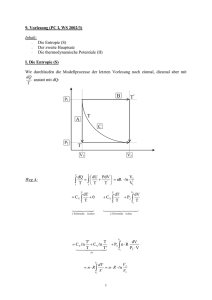
Stoffgleichgewicht (Materiegleichgewicht)
Die Hauptsätze der Thermodynamik beziehen sich auf die Zustandsfunktionen Temperatur T, innere
Energie U und Entropie S.
0. HS
1. HS
→T
→U
dU = δq + δw
ΔU = q + w
2. HS
→S
δq
dS ≥
T
q
ΔS ≥
T
Der zweite Hauptsatz erlaubt es, zu bestimmen, ob ein Prozess möglich ist oder nicht.
Bei einem isolierten System, z.B. im Universum, wird keine Wärme mit der Umgebung ausgetauscht:
δ q = 0 (isoliertes System)
dSisoliertes System ≥ 0
dSUniv ≥ 0
Ein Prozess, bei dem die Entropie des Universums SUniv abnimmt ist deshalb thermodynamisch
unmöglich.
nicht möglich
dSUniv < 0
Ein Prozess, bei dem SUniv zunimmt ist thermodynamisch möglich und irreversibel.
irreversibel
dSUniv > 0
Bei reversiblen Prozessen ist SUniv konstant, bzw. ΔSUniv = 0 .
reversibel
dSUniv = 0
Solche reversiblen Prozesse sind im Prinzip möglich, aber in der Praxis schwer zu erreichen.
Das Entropiekriterium für isolierte Systeme soll im Folgenden dazu benutzt werden, um Bedingungen
für Stoffgleichgewicht in einem geschlossenen System zu formulieren. Diese Bedingungen sollen
mithilfe geeigneter Zustandsfunktionen des Systems formuliert werden.
Die Gleichgewichtsbedingung für isolierte Systeme bedeutet die Maximierung der Entropie.
Für geschlossene Systeme ergeben sich spezielle Gesetze.
Materie- bzw. Stoffgleichgewichte können sich auf chemische Reaktionen oder Phasenumwandlungen
beziehen. In beiden Fällen liegen in allen Phasen konstante Stoffmengen für jede Komponente vor.
1
Entropie und Gleichgewicht
Wir betrachten nochmals zunächst ein isoliertes System, das sich nicht im Stoffgleichgewicht befindet.
Freiwillig ablaufende chemische Reaktionen oder Stoffaustausch zwischen verschiedenen Phasen im
System stellen irreversible Prozesse dar, welche die Entropie des Systems erhöhen. Diese Prozesse
dauern an, bis die Entropie des Systems ein Maximum erreicht. Weitere Prozesse könnten die Entropie
nur erniedrigen, was aber gegen den 2. Hauptsatz verstoßen würde.
Kriterium für Stoffgleichgewicht für ein isoliertes System: Maximierung der Entropie S.
Ein geschlossenes System kann Wärme und Arbeit mit der Umgebung austauschen. System und
Umgebung stellen insgesamt wieder ein isoliertes System dar.
Kriterium für Stoffgleichgewicht für ein geschlossenes System:
Maximierung der Gesamtentropie Sges von System und Umgebung.
Chemische Reaktionen und Phasenumwandlungen im geschlossenen System werden ablaufen bis
S ges = S Syst + SUmg maximiert ist.
Meist sind die thermodynamischen Eigenschaften der Umgebung nicht von Interesse. Obwohl ein
Kriterium für Stoffgleichgewicht in einem geschlossenen System nun bereits vorliegt, wäre es
wünschenswert ein Kriterium zu finden, das sich nur auf Eigenschaften des Systems bezieht.
Abb. 1: Geschlossenes System im thermischen und mechanischen Gleichgewicht, aber ohne
Stoffgleichgewicht.
Abbildung 1 soll helfen, ein gutes Gleichgewichtskriterium zu finden. Das geschlossene System besitzt
dieselbe Temperatur wie die Umgebung. System und Umgebung sind vom Rest der Welt isoliert. Das
System befindet sich also im thermischen und mechanischen Gleichgewicht, aber nicht im
Stoffgleichgewicht. Die Umgebung soll aber ständig im thermodynamischen Gleichgewicht
(thermisches, mechanisches und Stoffgleichgewicht) sein. Das System kann mit der Umgebung
Energie austauschen (in Form von Arbeit und Wärme), aber keine Materie.
2
Während der chemischen Reaktion oder dem Stofftransport zwischen verschiedenen Phasen im System
sollen thermisches und mechanisches Gleichgewicht stets erhalten bleiben.
Hinweis: Das bedeutet nicht unbedingt, dass Temperatur und Druck während des Prozesses konstant
sein müssen (diese Größen könnten sich langsam ändern, man spricht von währendem Gleichgewicht).
Bei einem Wärmeaustausch gilt:
δqUmg = −δqSyst
Weil die chemische Reaktion oder der Stofftransport innerhalb des Systems, das sich noch nicht im
Stoffgleichgewicht befindet, irreversibel ist, muss die Änderung der Gesamtentropie positiv sein:
dS ges = dS Syst + dSUmg > 0
Die Umgebung bleibt nach wie vor im thermodynamischen Gleichgewicht. Deshalb ist dort der
Wärmeaustausch reversibel:
δqUmg
dSUmg =
T
Weil das System nicht im thermodynamischen Gleichgewicht ist, beinhalten die Prozesse eine
−δqUmg δqSyst
irreversible Änderung. Die letzten drei Gleichungen ergeben: dS Syst > −dSUmg =
.
=
T
T
δqSyst
Deshalb gilt dS Syst >
, bzw.
T
δq
(geschlossenes System, thermisches und mechanisches Gleichgewicht)
dS > irrev
T
Von hier ab wird der Index Syst weggelassen, weil sich alle Größen ohnehin auf das System beziehen.
Wenn das System das Stoffgleichgewicht erreicht hat, können alle unendlich kleinen Änderungen als
reversibel betrachtet werden.
δq
Im Stoffgleichgewicht gilt deshalb: dS = rev .
T
Zusammengefasst ergibt sich:
δq
dS ≥
Clausius Ungleichung
T
(Änderung der Stoffmenge im geschlossenen System, thermisches und mechanisches GG).
Die mit der Umgebung ausgetauschte Wärmemenge ist laut erstem Hauptsatz δq = dU − δw . Diesen
Ausdruck kann man in die Clausius Ungleichung einsetzen. Für ein geschlossenes System im
mechanischen und thermischen Gleichgewicht folgt also:
dU ≤ TdS + δw
(Änderung von Stoffmengen im geschlossenen System, thermisches und mechanisches GG).
Das Gleichheitszeichen bezieht sich jeweils auf das Stoffgleichgewicht.
3
Freie Energie F und Freie Enthalpie G
Der Ausdruck dU ≤ TdS + δw wird nun benutzt, um Bedingungen für Stoffgleichgewicht in Form von
Zustandsfunktionen abzuleiten.
1. Fall: Geschlossenes System bei konstanter Temperatur T und konstantem Volumen V.
Während der irreversiblen Annäherung an das Gleichgewicht gilt dV = 0 und dT = 0 . Um die
Temperatur ins Spiel zu bekommen, wird SdT addiert und subtrahiert:
dU ≤ TdS + SdT − SdT + δw
Wegen der Produktregel d( uv ) = udv + vdu ergibt sich
dU ≤ d( TS ) − SdT + δw
Die Beziehung d( u + v ) = du + dv liefert
d(U − TS ) ≤ − SdT + δw
Zunächst erlauben wir nur Volumenarbeit, δw = − pdV :
d(U − TS ) ≤ − SdT − pdV
Bei konstanter Temperatur T und konstantem Volumen V erhalten wir
d(U − TS ) ≤ 0
(T und V konstant, geschlossenes System, thermisches und mechanisches GG, nur Volumenarbeit)
Bei einem geschlossenen System mit konstanter Temperatur und konstantem Volumen wird die
Zustandsfunktion U − TS während der freiwilligen, irreversiblen Gleichgewichtseinstellung
kontinuierlich kleiner werden. Im Stoffgleichgewicht wird U − TS ein Minimum erreicht haben, dann
gilt d(U − TS ) = dF = 0 . Dieses Ergebnis ist offensichtlich eine Konsequenz des 1. und 2. Hauptsatzes.
Die Zustandsfunktion U − TS wird Helmholtz-Energie, Freie Energie F oder Arbeitsfunktion A
genannt.
F ≡ U − TS
(39a)
A ≡ U − TS
Wird der Zustand eines Systems bei konstanter Temperatur verändert, gilt:
dF = dU − TdS
(40a)
4
2. Fall: Geschlossenes System bei konstanter Temperatur T und konstantem Druck p.
Während der irreversiblen Annäherung an das Gleichgewicht gilt dp = 0 und dT = 0 . Um die
Temperatur und den Druck ins Spiel zu bekommen, werden SdT und Vdp addiert und subtrahiert, etc:
dU ≤ TdS + SdT − SdT − pdV + Vdp − Vdp
dU ≤ d( TS ) − SdT − d( pV ) + Vdp
d(U + pV − TS ) ≤ − SdT + Vdp
d( H − TS ) ≤ − SdT + Vdp
Bei konstanter Temperatur T und konstantem Druck p erhalten wir
d( H − TS ) ≤ 0
(T und p konstant, geschlossenes System, thermisches und mechanisches GG, nur Volumenarbeit)
Bei einem geschlossenen System mit konstanter Temperatur und konstantem Druck wird die
Zustandsfunktion H − TS während der freiwilligen, irreversiblen Gleichgewichtseinstellung
kontinuierlich kleiner werden. Im Stoffgleichgewicht wird H − TS ein Minimum erreicht haben, dann
gilt d( H − TS ) = dG = 0 . Dieses Ergebnis ist ebenfalls eine Konsequenz des 1. und 2. Hauptsatzes.
Die Zustandsfunktion H − TS wird Gibbs-Energie oder Freie Enthalpie G genannt.
G ≡ H − TS ≡ U + pV − TS
(39b)
Wird der Zustand eines Systems bei konstanter Temperatur verändert, gilt:
dG = dH − TdS
(40a)
Abb. 2: Für ein geschlossenes System, das nur Volumenarbeit leisten kann, wird die Freie Enthalpie G
minimiert, wenn sich bei konstanter Temperatur und konstantem Druck ein thermodynamisches
Gleichgewicht einstellt.
5
Die Freie Enthalpie G wird während der Gleichgewichtseinstellung (bei T und p konstant) immer
kleiner und erreicht im Gleichgewicht ein Minimum. Gleichzeitig erhöht sich die Entropie im
Universum. Die Freie Enthalpie G ist wie U , V und S eine extensive Größe.
Zusammenfassung - Bedingungen für spontane Vorgänge und Stoffgleichgewicht:
In einem geschlossenen System, das nur Volumenarbeit verrichten kann, ist die Bedingung für
spontane Vorgänge und Stoffgleichgewicht bei konstanter Temperatur T und konstantem Volumen V
die Minimierung der Freien Energie F und bei konstanter Temperatur T und konstantem Druck p die
Minimierung der Freien Enthalpie G .
( dF )T ,V ≤ 0
(41)
( dG )T ,p ≤ 0
Ein geschlossenes System strebt möglichst kleine Werte für F bzw. für G an. Wegen
dF = dU − d( TS ) und dG = dH − d( TS ) sind Energieerniedrigung und Entropieerhöhung Triebkräfte
für chemische Reaktionen und Phasenumwandlungen.
Anmerkung: Für die Entropieänderung in der Umgebung gilt ΔSUmg =
Weil der Druck konstant ist, folgt ΔSUmg =
qUmg
T
=
− qSyst
T
.
−ΔH Syst
.
T
Wegen G ≡ H − TS gilt bei konstanter Temperatur ΔG = ΔH − T ΔS .
Insgesamt ändert sich die Entropie im Universum:
ΔSUniv =
−ΔH Syst
+ ΔS Syst =
T
konstant, nur Volumenarbeit)
−( ΔH Syst − T ΔS Syst )
T
=
−ΔGSyst
T
(geschlossenes System, T und p
Die Abnahme von GSyst während der Gleichgewichtseinstellung (bei T und p konstant) entspricht einer
proportionalen Erhöhung der Gesamtentropie (Entropie des Universums). Dies ist sowohl für
exotherme Reaktionen (Erhöhung der Entropie in der Umgebung) als auch für endotherme Reaktionen
(Erhöhung der Entropie im System) denkbar.
Weitere Bedeutung von F
Die Bezeichnungen "Arbeitsfunktion" und "Freie Energie" für F haben ihre Gründe. Bevor nur
Volumenarbeit zugelassen wurde, konnte formuliert werden (s.o.):
dF ≤ − SdT + δw
Der Betrag der maximal vom System geleisteten Arbeit bei konstanter Temperatur ist −δwmax = − dF .
Für einen endlichen isothermen Prozess gilt
− w ≤ −ΔF
(42a)
(T konstant, geschlossenes System)
6
Das bedeutet, dass die von einem System geleistete Arbeit kleiner oder gleich der negativen Änderung
der Zustandsfunktion F ist. Daher rührt die Bezeichnung Arbeitsfunktion. Das Gleichheitszeichen gilt
wieder für den reversiblen Prozess. Für eine gegebene Zustandsänderung ist −ΔF eine feste Größe.
Daher wird die maximale Arbeit − wmax von einem System nur bei reversibler Prozessführung geleistet.
Anmerkung: Der Maximalbetrag an Arbeit kann größer oder kleiner sein als −ΔU , die negative
Änderung der inneren Energie des Systems. Für jeden beliebigen Prozess in einem geschlossenen
System gilt nach dem 1. Hauptsatz − wmax = − ΔU + q = − ΔU + T ΔS . Die ausgetauschte Wärmemenge
entspricht gerade der Differenz zwischen −w und −ΔU . Beispiel: Im Carnot Kreisprozess ist ΔU = 0
und − w > 0 .
Erfolgt beim Vorgang eine Entropieabnahme ( q < 0 ), ist − wmax < −ΔU .
Ein Teil der Energie aus dem System muss in die Umgebung, damit dort genügend Entropie erzeugt
wird, um die Entropieabnahme im System zu kompensieren.
Erfolgt beim Vorgang eine Entropiezunahme ( q > 0 ), ist − wmax > −ΔU .
Das System nimmt Energie in Form von Wärme aus der Umgebung auf.
Weitere Bedeutung von G
Bei konstanter Temperatur und konstantem Druck ist das Kriterium für eine spontan ablaufende
Reaktion (41):
( dG )T ,p ≤ 0
D.h., Reaktionen laufen freiwillig ab, wenn dabei die Freie Enthalpie abnimmt:
ΔG = GPr odukte − GEdukte . Nur wenn ΔG negativ ist, läuft die Reaktion freiwillig ab (exergonisch). Die
Rückreaktion wäre dann endergonisch und müsste erzwungen werden.
ΔG = ΔH − T ΔS suggeriert, dass man zwei Triebkräfte hat: Abnahme der Enthalpie und Zunahme der
Entropie. Tatsächlich ist die eigentliche Triebkraft die Entropiezunahme im Gesamtsystem, im Weltall.
Das Wechselspiel zwischen Entropiezunahme und Enthalpieabnahme führt dazu, dass auch endotherme
Reaktionen (d.h. Δ H > 0 ) spontan ablaufen können. Das setzt voraus, dass die Entropiezunahme
( T ΔS ) die Enthalpiezunahme (und damit die Entropieabnahme in der Umgebung) überkompensiert.
Auch ΔG kann mit der maximalen Arbeit in Beziehung gebracht werden.
Wegen G = F + pV ergibt sich dG = dF + pdV + Vdp . Daraus folgt für ein geschlossenes System im
thermischen und mechanischen Gleichgewicht
dG ≤ − SdT + δ w + pdV + Vdp
Bei konstanter Temperatur und konstantem Druck ist
dG ≤ δ w + pdV
(T, p konstant, geschlossenes System)
7
Arbeit kann in Volumenarbeit und Nicht-Volumenarbeit bzw. Extra-Arbeit δ we (meist elektrische
Arbeit) aufgeteilt werden. Damit erhält man
dG ≤ − pdV + δ we + pdV
dG ≤ δ we
ΔG ≤ we
bzw. für den Betrag von geleisteter Nicht-Volumenarbeit
− we ≤ − ΔG
(T, p konstant, geschlossenes System)
− ΔG entspricht im reversiblen Fall dem Maximum der Nicht-Volumenarbeit, die das System leisten
kann. Daher die Bezeichnung Freie Enthalpie.
− we,max = − ΔG
(42b)
Wenn nur Volumenarbeit geleistet wird, gilt für einen reversiblen, isothermen und isobaren Prozess
natürlich ΔG = 0 .
Beispiele für Nicht-Volumenarbeit in biologischen Systemen sind die Arbeit bei Muskelkontraktion
und die Übertragung von Nervenimpulsen.
Bei elektrochemischen Reaktionen hängt die Freie Reaktionsenthalpie ΔGr im reversiblen Fall mit der
leicht zu bestimmenden elektrischen Arbeit zusammen:
ΔGr = − zFE
Hierbei sind
z
F = e⋅ NA
− zF
E
Anzahl ausgetauschter Elektronen pro Formelumsatz
Faradaykonstante (nicht mit Freier Energie verwechseln!)
ausgetauschte Ladungsmenge
reversible Zellspannung
− zFE
maximale elektrische Arbeit
8
Die Berechnung der Entropie
Wir haben bereits die Temperaturabhängigkeit von S diskutiert und gesehen, dass die Kenntnis von
c p eine wichtige Rolle spielt.
Aus den Definitionsgleichungen dS =
δ qrev
T
und ( δ qrev )p = dH = c p dT folgt:
S( TE ) = S( TA ) +
TE
cp
∫
TA
T
dT
Wir können die Entropie eines Systems (z.B. einer chemischen Substanz) bestimmen, indem wir die
Integration von T = 0 K bis zur Temperatur T durchführen. Dabei wird die Umwandlungsentropie
ΔHt
für jeden auftretenden Phasenübergang dazuaddiert.
Δ St =
Tt
S( T ) = S( 0 ) +
Tmelt
∫
0
c p,( s )
T
dT +
Δ H melt
Tmelt
Tvap
∫
+
Tmelt
c p,( l )
T
dT +
Δ H vap
Tvap
T
+
∫
c p,( g )
Tvap
T
dT
(43)
Für die Berechnung der Standardentropie S ° wird bis zur Temperatur 298,15 K integriert.
Mit Ausnahme von S( 0 ) kann man alle Größen kalorimetrisch bestimmen. Problematisch ist die
Messung von c p in der Nähe des absoluten Nullpunkts der Temperatur. Aufgrund von Arbeiten von
Peter Debye weiß man jedoch, dass für sehr tiefe Temperaturen gilt: c p ∼ T 3 .
Mit c p = aT 3 ist
T
S( T ) − S( 0 ) = ∫
0
cp
T
1
a
dT = ∫ aT 2 dT = T 3 = c p ( T )
3
3
T
0
Abb. 3: Temperaturabhängigkeit von cp/T und S.
9
S(0) und der 3. Hauptsatz der Thermodynamik
Entropieänderungen können mithilfe des 2. Hauptsatzes und cp-Messungen berechnet werden.
Wie erhält man absolute Entropien?
Um die Standardentropien berechnen zu können, brauchen wir noch einen Zahlenwert für S(0).
Am absoluten Nullpunkt ist alle Energie, soweit das möglich ist, dem Körper entzogen.
In einem perfekten Kristall ohne Fehlstellen sind bei T = 0 K alle Teilchen regelmäßig angeordnet, die
thermische Unordnung ist verschwunden, so dass wir eigentlich annehmen dürfen, dass der Körper die
Entropie Null hat.
Können wir diese Überlegungen in einem Hauptsatz formulieren?
Ähnlich wie beim 2. Hauptsatz gab es dazu mehrere Versuche.
Normalerweise werden keine Standardbildungsentropien tabelliert.
Jedes Element erhält einen Entropiewert für einen bestimmten Referenzzustand.
Dann wird ΔS für den Prozess der Bildung von Verbindungen im Standardzustand berechnet.
Referenzzustand:
Reines Element in der stabilsten Modifikation bei 1 bar (Standarddruck) und T → 0 K .
Die molare Entropie jedes Elements in diesem Zustand sei Null.
°
°
Sm,
0 = lim Sm,T = 0
T →0
(Element, ° bedeutet 1 bar)
ΔS für die Bildung von Verbindungen kann nicht leicht gemessen werden, vor allem weil die
q
Reaktionswärme irreversibel ist und ΔS = nicht benutzt werden kann.
T
1) Es ist unmöglich, den absoluten Nullpunkt in einer endlichen Anzahl von Schritten zu erreichen.
Dass der absolute Nullpunkt unerreichbar ist, kann auch aus dem Carnot-Wirkungsgrad geschlossen
T
werden: η = 1 − k . Tk = 0 K würde η = 1 ergeben, was dem 2. Hauptsatz widerspricht.
Tw
2) T.W. Richards hat 1900 Messungen von ΔG ° vs. T vorgestellt.
W. Nernst schloss daraus, dass lim ΔS = 0 sein muss.
T →0
Nernst Wärmesatz: Die Entropieänderung, die mit einem isothermen Prozess zwischen kondensierten
Phasen verbunden ist, die im internen Gleichgewicht vorliegen, geht für T → 0 K gegen Null.
(Bei unterkühltem Helium liegt z.B. kein internes Gleichgewicht vor)
10
Aus diesem Grund ist die Entropie nicht nur von Elementen, sondern auch von chemischen
Verbindungen im internen Gleichgewicht im Referenzzustand Null: S0° = lim S ° = 0
T →0
lim S = S( 0 ) = 0
T →0
Eine isotherme Änderung des Drucks wird ebenfalls lim ΔS = 0 zeigen. Deshalb ist die Entropie von
T →0
Elementen und Verbindungen bei T → 0 K unabhängig vom Druck Null.
Die quantenmechanische bzw. statistische Betrachtung liefert den Ausdruck, der sinngemäß auf dem
Grabstein von L. Boltzmann steht.
S( 0 ) = k B ln( Ω )
3) Der 3. Hauptsatz: Setzt man die Entropie jedes Elements in seinem stabilsten Zustand bei
T = 0 K gleich Null, so hat jede Verbindung eine positive Entropie. Sie kann bei T = 0 K den Wert Null
annehmen und tut dies, wenn die Verbindung als perfekter Kristall vorliegt.
3. Hauptsatz der Thermodynamik
Die Entropie aller perfekten Materialien ist bei T = 0 K gleich Null.
Entropien von Substanzen, die mittels der Festlegung S( 0 ) = 0 berechnet worden sind, nennt man
„Third Law Entropies“.
-1
-1
S° / J K mol
C (Diamant)
2.4
C (Graphit)
5.7
Cu(s)
33.2
Ag(s)
42.6
Na(s)
51.2
H2O(l)
69.9
Hg(l)
76.0
C6H6(l)
173.3
He(g)
126.2
H2(g)
130.7
N2(g)
192.1
CO2(g)
213.7
NH3(g)
192.5
H2S(g)
205.8
11
Standardentropie S° / J K-1 mol-1
250
200
150
100
50
H2S(g)
NH3(g)
CO2(g)
N2(g)
H2(g)
He(g)
C6H6(l)
Hg(l)
H2O(l)
Na(s)
Ag(s)
Cu(s)
C (Graphit)
C (Diamant)
0
Die Standardentropien der Gase (mit Ausnahme von H2 und der Edelgase) sind sehr ähnlich.
Die Standardreaktionsentropie Δ r S °
Differenz der Entropien der reinen Reaktionsprodukte, die sich alle in ihren Standardzuständen
befinden.
Für die Reaktion 0 = ∑ ν J J ist
J
Δ r S ° = ∑ ν J S J°
(44)
J
Die Freie Standardreaktionsenthalpie Δ r G°
Definition: Δ r G° = Δ r H ° − T Δ r S °
Standardreaktionsenthalpie Δ r H °
Standardreaktionsentropie Δ r S °
Die Freie Standard-Bildungsenthalpie ΔbG°
12
ΔbG° ist die Änderung der Freien Enthalpie pro mol Substanz bei der Bildung der Verbindung aus den
Elementen, wobei sich alle Substanzen bei der angegebenen Temperatur in ihren Standardzuständen
befinden.
Für die Elemente wird ΔbG° = 0 festgelegt.
ΔbG° / kJ mol-1 ΔbH° / kJ mol-1
C (Diamant)
2.9
1.9
C (Graphit)
0.0
0.0
-237.1
-285.8
H2O(l)
124.3
49.0
C6H6(l)
CO2(g)
-394.4
-393.5
NH3(g)
-16.5
-46.1
H(g)
203.3
218.0
Für die Reaktion 0 = ∑ ν J J ist
J
Δ r G° = ∑ ν J ΔbGJ°
(45)
J
13
Kombination von 1. und 2. Hauptsatz
Ziel: Ableitung neuer Beziehungen zwischen den Zustandsgrößen.
1. Hauptsatz
dU = δq + δw
ΔU = q + w
Für reversible Änderungen in einem geschlossenen System gilt δq = TdS
In Abwesenheit von Nicht-Volumenarbeit gilt δw = − pdV
Wir erhalten unter diesen Bedingungen eine Fundamentalgleichung der Thermodynamik
dU = TdS − pdV
(46)
Merke: Diese Gleichung gilt für jeden beliebigen Vorgang (reversibel oder irreversibel), da U eine
Zustandsfunktion ist.
Irreversibler Fall: δq < TdS und −δw < pdV .
In der Fundamentalgleichung (46) haben wir U(S,V).
Es gilt dann das totale Differential:
⎛ ∂U
dU = ⎜
⎝ ∂S
⎞
⎛ ∂U
⎟ dS + ⎜
⎠V
⎝ ∂V
⎞
⎟ dV
⎠S
Durch Vergleich erhalten wir:
⎛ ∂U ⎞
⎜
⎟ =T
⎝ ∂S ⎠V
⎛ ∂U ⎞
⎜
⎟ = −p
⎝ ∂V ⎠ S
Wir bilden nun die 2. Ableitung von U nach V bzw. S:
∂ 2U ⎛ ∂T ⎞
=⎜
⎟
∂V ∂S ⎝ ∂V ⎠ S
∂ 2U
⎛ ∂p ⎞
= −⎜ ⎟
∂S ∂V
⎝ ∂S ⎠V
nach dem Satz von Schwarz gilt deshalb
∂ 2U ⎛ ∂T
=⎜
∂V ∂S ⎝ ∂V
∂ 2U
⎞
⎛ ∂p ⎞
=
−
=
⎟
⎜ ⎟
⎠S
⎝ ∂S ⎠V ∂S ∂V
14
Aus der Fundamentalgleichung dU = TdS − pdV und den Definitionen der anderen
thermodynamischen Zustandsfunktionen werden weitere drei Fundamentalgleichungen erhalten.
1. Hauptsatz,
dU = δq + δw
Definitionen:
H ≡ U + pV
F ≡ U − TS
G ≡ H − TS
Fundamentalgleichungen
dU = TdS − pdV
(46)
dH = dU + pdV + Vdp
dH = TdS − pdV + pdV + Vdp
dH = TdS + Vdp
(47)
dF = dU − TdS − SdT
dF = TdS − pdV − TdS − SdT
dF = − pdV − SdT
(48)
dG = dH − TdS − SdT
p und T sind die wichtigsten Variablen in der Chemie:
dG = TdS + Vdp − TdS − SdT
dG = Vdp − SdT
(49)
Man erkennt folgende partielle Ableitungen:
⎛ ∂U ⎞
⎛ ∂H ⎞
T =⎜
⎟ =⎜
⎟
⎝ ∂S ⎠V ⎝ ∂S ⎠ p
⎛ ∂U ⎞
⎛ ∂F ⎞
p = −⎜
⎟ = −⎜
⎟
⎝ ∂V ⎠ S
⎝ ∂V ⎠T
⎛ ∂H
V =⎜
⎝ ∂p
⎞
⎛ ∂G ⎞
⎟ =⎜
⎟
⎠ S ⎝ ∂p ⎠T
⎛ ∂F ⎞
⎛ ∂G ⎞
S = −⎜
⎟ = −⎜
⎟
⎝ ∂T ⎠V
⎝ ∂T ⎠ p
Besonders wichtig ist die T- und p-Abhängigkeit von G:
⎛ ∂G ⎞
⎜
⎟ = −S
⎝ ∂T ⎠ p
(49a)
⎛ ∂G ⎞
⎜
⎟ =V
⎝ ∂p ⎠T
(49b)
15
Die Maxwell Beziehungen
Diese Beziehungen werden aus den zweiten Ableitungen erhalten (Satz von Schwarz)
⎛ ∂T ⎞
⎛ ∂p ⎞
⎜
⎟ = −⎜ ⎟
⎝ ∂V ⎠ S
⎝ ∂S ⎠V
⎛ ∂S
⎜
⎝ ∂V
⎞
⎛ ∂p ⎞
⎟ =⎜
⎟
⎠T ⎝ ∂T ⎠V
⎛ ∂T ⎞
⎛ ∂V ⎞
⎜⎜
⎟⎟ = ⎜
⎟
⎝ ∂p ⎠ S ⎝ ∂S ⎠ p
⎛ ∂S ⎞
⎛ ∂V
−⎜ ⎟ = ⎜
⎝ ∂p ⎠T ⎝ ∂T
⎞
⎟
⎠p
⎛ ∂U ⎞
Bei der Behandlung des 1. Hauptsatzes spielte der Binnendruck ⎜
⎟ eine wichtige Rolle.
⎝ ∂V ⎠T
Jetzt können wir mithilfe der Fundamentalgleichung dUT = TdST − pdVT bei konstanter Temperatur
direkt ableiten:
dUT ⎛ ∂U ⎞
⎛ ∂S ⎞
⎛ ∂p ⎞
=⎜
⎟ =T ⎜
⎟ − p =T⎜
⎟ −p
dVT ⎝ ∂V ⎠T
⎝ ∂V ⎠T
⎝ ∂T ⎠V
⎛ ∂U ⎞
Joule hatte im Experiment versucht nachzuweisen, dass für ein ideales Gas ⎜
⎟ =0.
⎝ ∂V ⎠T
Dies lässt sich mit obiger Gleichung direkt beweisen (ohne Experiment).
nRT
V
Für das ideale Gas gilt:
p=
Dann gilt
nR
⎛ ∂p ⎞
⎜
⎟ =
⎝ ∂T ⎠V V
⎛ ∂U
⎜
⎝ ∂V
!
nR
⎞
⎛ ∂p ⎞
− p=0
⎟ =T ⎜
⎟ − p =T
V
⎠T
⎝ ∂T ⎠V
D.h. die innere Energie eines idealen Gases ist unabhängig vom Volumen.
Die innere Energie eines idealen Gases hängt lediglich von der Temperatur ab.
16
Die Temperaturabhängigkeit von G
⎛ ∂G ⎞
Wir haben abgeleitet: ⎜
⎟ = −S
⎝ ∂T ⎠ p
Da S immer positiv ist, folgt, dass bei einer T-Erhöhung G abnimmt ( p = const ). Diese Abnahme ist
umso größer, je größer S ist.
Wir ersetzen die Entropie durch die Enthalpie mithilfe der Definitionsgleichung:
G ≡ H − TS
S=
H −G
T
G−H
⎛ ∂G ⎞
Damit erhalten wir: ⎜
⎟ =
T
⎝ ∂T ⎠ p
bzw.
G
H
⎛ ∂G ⎞
⎜
⎟ − =−
T
⎝ ∂T ⎠ p T
Differentialregel für Quotienten (Ableitung der Funktion G/T):
⎛G⎞
⎛ 1⎞
∂⎜ ⎟
⎜ ∂ T ⎟ 1 ⎛ ∂G ⎞ G 1 ⎛ ⎛ ∂G ⎞ G ⎞
∂
1
G
T
⎛
⎞
⎝ ⎠=
+
G
⎜
⎟= ⎜
⎜
⎟
⎟ − 2 = ⎜⎜
⎟−
∂T
T ⎝ ∂T ⎠
T ⎝ ⎝ ∂T ⎠ T ⎟⎠
⎜ ∂T ⎟ T ⎝ ∂T ⎠ T
⎝
⎠
Daraus erhalten wir die Gibbs-Helmholtz-Gleichung:
1 ⎛ ⎛ ∂G ⎞
G⎞
H
⎛ ∂( G / T ) ⎞
⎜
⎟=−
=
−
⎜
⎟
⎜
⎟
⎝ ∂T
⎠ p T ⎜⎝ ⎝ ∂T ⎠ p T ⎟⎠
T2
(50)
Für eine Reaktion gilt entsprechend:
ΔH
⎛ ∂( ΔG / T ) ⎞
⎜
⎟ =− 2
∂T
⎝
⎠p
T
(50a)
17
Die Druckabhängigkeit von G
⎛ ∂G ⎞
Es gilt ⎜
⎟ =V
⎝ ∂p ⎠T
Damit ist
G( p2 ) = G( p1 ) +
p2
∫ Vdp
p1
Wir unterscheiden wieder zwischen Festkörpern und Flüssigkeiten, bei denen sich V nur sehr wenig mit
p ändert, und Gasen, wo man die bekannte starke Druckabhängigkeit von V hat.
1. Fall: Festkörper und Flüssigkeiten
G( p2 ) = G( p1 ) + V ( p2 − p1 ) ≈ G( p1 )
V und Δp sind in der Regel klein. Die kleine Korrektur kann oft vernachlässigt werden.
Beispiel: Flüssiges Wasser
ΔbG° = −273 kJ mol −1
V ≈ 18 cm3 mol −1
p1 = 1 bar
p2 = 10 bar
G( 10 bar ) = −273, 0 kJ mol −1 + 18 cm3 mol −1 ⋅
10−6 m3
cm3
⋅ 9 bar ⋅
105 Pa
= −272,98 kJ mol −1
bar
2. Fall: Ideales Gas
G( p2 ) = G( p1 ) + nRT
p2
∫
p1
dp
p
⎛p ⎞
G( p2 ) = G( p1 ) + nRT ln ⎜ 2 ⎟
⎝ p1 ⎠
(51)
RT ≈ 8,314 J K −1 mol −1 ⋅ 300 K ≈ 2,5 kJ mol −1
Bei Raumtemperatur hat eine Druckerhöhung um den Faktor 10 eine Zunahme von G um etwa
2 ,3 ⋅ 2 ,5 kJ mol −1 = 5, 75 kJ mol −1 zur Folge.
18