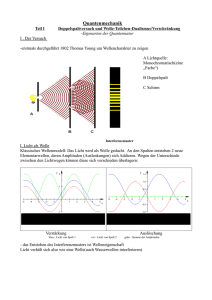
5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900
Werbung

1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900 5.2. Der Photoelektrische Effekt - Beobachtungen - Einsteins Interpretation - Impuls und Energieerhaltung 5.3. Der Comptoneffekt 5.4. Die Plancksche Strahlungformel 5.5. Licht als Welle und Teilchen 6. Teilchen als Welle (de Broglie) 7. Heisenbergsche Unschärferelation 8. Das Bohrsche Atomodell 9. Grundlagen der Quantenmechanik 10. Quantenmechanik des Wasserstoffatoms 5. Das Photon: Welle und Teilchen Newton: (18. Jahrh.) Licht sind kleine Teilchen Huygens: (19. Jahrh.) Licht ist eine Welle 5. Das Photon: Welle und Teilchen Newton: Teilchen α α Reflektion: Einfallswinkel=Ausfallwinkel ABER: Wellen werden auch reflektiert! (Stehende Welle) 5. Das Photon: Welle und Teilchen Newton: Teilchen α ABER: Wellen können unterschiedliche Ausbreitungsgeschwindigkeit haben Newton: Brechung durch Kraft an der Oberfläche 5. Das Photon: Welle und Teilchen Huygens: Welle Huygensches Prinzip: Jede Welle zerlegbar in Überlagerung von Kugelwellen 5. Das Photon: Welle und Teilchen Interferenz und Beugung z.B. Thomas Young Doppelspalt (1801) 5. Das Photon: Welle und Teilchen Huygens: Welle z.B. Interferenz an dünnen Schichten: 5. Das Photon: Welle und Teilchen Welche Art Welle? 5. Das Photon: Welle und Teilchen 1885 Maxwell Gleichungen 1887 Heinrich Hertz: Elektromagnetische Wellen kann man durch Ladungsbewegung aussenden durch Antenne Auffangen Funkenentladung Sender Induzierte Entladung Empfänger Antenne 5. Das Photon: Welle und Teilchen 1885 Maxwell Gleichungen 1887 Heinrich Hertz: Elektromagnetische Wellen kann man durch Ladungsbewegung aussenden durch Antenne Auffangen lt a p s l oppe &D z t r e H & l l e s? Maxw e d l i b len l e W s e d g e Si 5. Das Photon: Welle und Teilchen 5.2. Der Photoelektrische Effekt 1888 Hallwachs (Schüler von H. Hertz): positive charge: Zinc + + + + Magnesium (UV-light needed) Electrometer positive Ladung: kein Effekt 5. Das Photon: Welle und Teilchen 5.2. Der Photoelektrische Effekt 1888 Hallwachs (Schüler von H. Hertz): negative charge: Zinc --- Magnesium (UV-light needed) Electrometer negative: schnelle Entladung positive Ladung: kein Effekt 5. Das Photon: Welle und Teilchen 1899 J.J. Thomson 1900 Elster & Gütel A ee- ee- + classical electrodynamics: oscillating optical light field accelerates electrons E(t) = A sin(2π ν t) A ∝ √ Intensity Electron energy should depend on light intensity! Beobachtung: eStrom steigt mit eLichtintensität! e 5. Das Photon: Welle und Teilchen 1899 J.J. Thomson 1900 Elster & Gütel 1900ff Lenard ee- A + 1/2mv 2 > Uqe goal: measure kinetic energy 1/2 mv2 potential - ee- 5. Das Photon: Welle und Teilchen monochromatic light 1899 J.J. Thomson 1900 Elster & Gütel 1900 Lenard ee- A ee- - usefull unit: 1 eV (“Electron Volt”) = 1.60219 10-19 J (WS) energy of an electron on a potential of 1 Volt 5. Das Photon: Welle und Teilchen 5.2. Der Photoelektrische Effekt Annalen der Physik, Band 17, Seite 132 (1905) 5. Das Photon: Welle und Teilchen 5.2. Der Photoelektrische Effekt Erklärung durch Einstein (1905): • Photoanregung = Elementarakt • Lichtwelle überträgt Energie in Quantenpaketen der Größe hν h= Plancksches Wirkungsquantum • Licht-“Teilchen“: Photonen Emax= hν- eUwork hν Ekin θ Nobelpreis 1921: „…in Anerkennung seiner Verdienste auf dem Gebiet der Theoretischen Physik und insbesondere für seine Entdeckung der Gesetze, auf denen die photoelektrische Wirkung beruht.“ Albert Einstein 5. Das Photon: Welle und Teilchen Millikan (Phys Rev. 7,355 (1916)) hν = eUwork (depends on material) h=6.56 10-34J sec within < 1% !! (6.626210-34J sec) e- Emax= hν- eUwork 5. Das Photon: Welle und Teilchen 5. Das Photon: Welle und Teilchen Photoelectric effect: energy and momentum conservation e- ehν e- hν e- Emax= hν- eUwork electron energy Ee= hν- Ebinding electron energy 5. Das Photon: Welle und Teilchen Photoelectric effect: energy and momentum conservation example: hν=99eV Ee= hν- Ebinding=75eV ke=5 10-24kg m/sec kphoton= h ν / c = 5.3 10-26kg m/sec nonrelativistic: photon momentum small ion or solid compensates electron momentum! (Eion=Ee*me/mion) ehν Photon cannot couple to a free electron, second particle needed! 5. Das Photon: Welle und Teilchen momentum Photoelectric effect: energy and momentum conservation eelectron 0 hν ion 0 momentum 99 eV, linear polarized γ + He -> He1+ + e- Photon cannot couple to a free electron, second particle needed! 5. Das Photon: Welle und Teilchen ehν Where do the momenta come from?? photon: No! acceleration ? 5. Das Photon: Welle und Teilchen Direction of photoelectrons: hν eee- changes directions, looses energy 5. Das Photon: Welle und Teilchen Direction of photoelectrons: 85 eV, linear polarized γ + He -> He1+(1s) + e- number of electrons ∝ sin2(θ) e- θ e! ! u r s t DAY y a TO w l t a PIC o N TO T HO hν intensity of radiation compare: Hertzian Oscillator electrons Energy 5. Das Photon: Welle und Teilchen Einstein: minimum frequency: hν = Ebinding 0 Ebind forbidden e- but ...: super high intensities Laser: example: hν = 1.5 eV << Ebind = 24 eV ehν not linear with intensity! I7 Lichtgeschosse: •3*3*3 μm3 •30 ... 6 femto Sekunden •Lichtgeschwindigkeit •Leistungsdichte 1016W/cm2 •0.2 milli Joule •1.25 106 GeV •2*1015 Photonen (a 1.5 eV) •Elektrische Felder > 1011 V/m Photo: S.Voss Atomic Units Solution of the time dependent Schrödinger Equation 2.0*1014W/cm2 800nm Daniel Dundas, Jonathan Parker Laura Moore Ken Taylor Queens University Belfast 1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900 5.2. Der Photoelektrische Effekt Zeigt die - Beobachtungen Quantelung der - Einsteins Interpretation Energie des Lichtes - Impuls und Energieerhaltung 5.3. Der Comptoneffekt 5.4. Die Plancksche Strahlungformel Zeigt direkt den Impuls des Photons 6. Teilchen als Welle (de Broglie) 7. Heisenbergsche Unschärferelation „Billard mit Photonen“ 8. Das Bohrsche Atomodell 9. Grundlagen der Quantenmechanik 10. Quantenmechanik des Wasserstoffatoms 11. Spin und Bahnmagnetismus 12 At i M tf ld 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt http://www.nobel.se/physics/laureates/1927/index.html 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt Blenden zur Richtungsbestimmung Graphit Block Hier findet die Compton Streuung Energiemessung statt Durch Braggstreuung Röntgenröhre Nachweis der Strahlung (Ja,Nein) 5. Das Photon: Welle und Teilchen Ablenkwinkel d d*sin(α) Bragg Bedingung für konstruktive Interferenz: 2d sin(α) = m * λ 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt Ursprüngliche Energie Niederenergetischere Strahlung winkelabhängig 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt λ’-λ= Δλ = h/m0c (1-cos(ϑ)) 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt different slit width (Slit1) 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt E‘=hν’ E=hν p=hν/c ϑ ϕ Elektron in Ruhe λ’-λ= Δλ = h/m0c (1-cos(ϑ)) Comptonformel nimmt an, das das Elektron vor dem Stoß ruht. Anfangimpulse der Elektronen müssen aber dazuaddiert werden. -> Comptonstreuung ist eine Methode um Impulsverteilungen von Elektronen zu messen 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt Die Impulsverteilung der Elektronen im Atom heißt bis heute “Comptonprofil” 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt It was in 1924 that I came across the theoretical paper by Bohr, Kramers, and Slater, which had just been published and which suggested a possible interpretation of the wave-particle dualism in the accepted description of the properties of light. This must be understood to mean the experimental fact that light of all wavelengths behaves as a wave process (interference) with pure propagation, but behaves as particles (light quanta: photo-effect, Compton effect) on conversion into other types of energy. The new idea consisted in denying strict validity to the energyimpulse law. In the individual or elementary process, so long as only a single act of emission was involved, the laws of conservation were held to be statistically satisfied only, to become valid for a macroscopic totality of a very large number of elementary processes only, so that there was no conflict with the available empirical evidence. It was immediately obvious that this question would have to be decided experimentally, before definite progress could be made. 1924 Bohr/Kramers/Slater statistische Deutung der Erhaltungssätze 1924/1925 Experiment: Bothe, Geiger Koinzidenzexperiment 5. Das Photon: Welle und Teilchen 1924/1925 Experiment: Bothe, Geiger Koinzidenzexperiment In this way we succeeded after a few failures to establish the accuracy of any temporal "coincidence" between the two pointer readings as being 10-4 sec. Film consumption however was so enormous that our laboratory with the film strips strung up for drying sometimes resembled an industrial laundry. Geiger zähler ϑ Geiger ϕ zähler Electrometer 5. Das Photon: Welle und Teilchen 5.3. Der Comptoneffekt 1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900 5.2. Der Photoelektrische Effekt - Beobachtungen - Einsteins Interpretation - Impuls und Energieerhaltung 5.3. Der Comptoneffekt 5.4. Die Plancksche Strahlungsformel 5.5. Licht als Welle und Teilchen 6. Teilchen als Welle (de Broglie) 7. Heisenbergsche Unschärferelation 8. Das Bohrsche Atomodell 9. Grundlagen der Quantenmechanik 10. Quantenmechanik des Wasserstoffatoms 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Hohe Temperaturen sind mit Erzeugung von e.m. Strahlung (Licht) verbunden: 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Spektrum der Hohlraumstrahlung: u(λ, T) u Messung von Lummer und Pringsheim (1900) 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Hohlraumstrahlung: Gleichgewicht von emittierter (Wände) und absorbierter Strahlung 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Harmonische Oszillatoren (schwingende Ladungen) Thermisch besetzter Oszillator 1/2kT kinetisch 1/2kT potenziell Thermisches Gleichgewicht Zwischen Absorbtion und Emission -> Spektrale Energiedichte Energie/Volumen = 8π/c3 kT ν2 dν = 8π kT / λ4 dλ Rayleigh, Jeans Strahlungsgesetzt Ultraviolett Katastrophe 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Rayleigh, Jeans Strahlungsgesetzt -> Spektrale Energiedichte Energie/Volumen = 8π/c3 kT ν2 dν = 8π kT / λ4 dλ Rayleigh, Jeans Strahlungsgesetzt Ultraviolett Katastrophe 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Spektrum der Hohlraumstrahlung: Experimentelle Ergebnisse Spektrum bei kleinen Frequenzen: u(ν , T ) ∝ ν 2T "Rayleigh-Jeans" Wellenlänge maximaler Intensität hängt von der Temperatur ab: Glühbirne λmax ⋅ T = const "Wien'sches Verschiebungsgesetz" Gesamte Strahlungsleistung: (Integral unter Kurve) ∞ ∫0 u(ν , T )dν = σT 4 Isolation! "StephanBoltzmannGesetz" 5. Das Photon: Welle und Teilchen 5.4. Die Plancksche Strahlungsformel Spektrum der Hohlraumstrahlung: u(λ, T) Plancksche Strahlungsformel (zunächst gefittet, später abgeleitet) u u (ν , T ) = Messung von Lummer und Pringsheim (1900) 8πh c 3 e hν ν3 k BT −1 5. Das Photon: Welle und Teilchen Harmonische Oszillatoren (schwingende Ladungen) Thermisch besetzter Oszillator 1/2kT kinetisch 1/2kT potentiell u (ν , T ) = 8πh c 3 e hν ν3 k BT −1 Thermisches Gleichgewicht Zwischen Absorbtion und Emission Plancks Annahme: harmonischer Oszillator kann nicht kontinuierlich absorbieren, sondern nur E= nh ν diskret Fitkonstante h=Plancksches Wirkungsquantum=6.626 10-34Js Energie 5. Das Photon: Welle und Teilchen Klassisch: kontinuierlich Planck: Diskret, Abstand h ν 5. Das Photon: Welle und Teilchen Die Geburtsstunde der Quantenmechanik ... lange vor der Quantenmechanik 14. Dezember 1900 Deutschen Physikalischen Gesellschaft in Berlin "Zur Theorie des Gesetzes der Energieverteilung im Normalspektrum„ Von Max Planck "Kurz zusammengefasst kann ich die ganze Tat als einen Akt der Verzweiflung bezeichnen. Denn von Natur bin ich friedlich und bedenklichen Abenteuern abgeneigt." 5. Das Photon: Welle und Teilchen Planck: black body radiation: quantized oscillators in the walls: Eresonator = nh ν Einstein: radiation itself is quantized Ephoton = h ν “Summing up, we may say that there is hardly one among the great problems, in which modern physics is so rich, to which Einstein has not made an important contribution. That he may have sometimes missed the target in his speculations, as, for example, in his hypothesis of light quanta (photons), cannot really be held too much against him, for it is not possible to introduce fundamentally new ideas, even in the most exact science, without occasionally taking a risk.” Max Planck praising Einstein in 1914 1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900 5.2. Der Photoelektrische Effekt Zeigt die - Beobachtungen Quantelung der - Einsteins Interpretation Energie des Lichtes - Impuls und Energieerhaltung 5.3. Der Comptoneffekt 5.4. Die Plancksche Strahlungformel Zeigt direkt den Impuls des Photons 5.5. Licht als Welle und Teilchen „Billard mit Photonen“ 6. Teilchen als Welle (de Broglie) 7. Heisenbergsche Unschärferelation 8. Das Bohrsche Atomodell 9. Grundlagen der Quantenmechanik 10. Quantenmechanik des Wasserstoffatoms 5. Das Photon: Welle und Teilchen 5.5. Licht als Welle und Teilchen – wie passt das zusammen? Ein Experiment in dem man Wellen und Teilchencharakter gleichzeitig sieht! Interferenzexperiment mit einem “Photonendetektor” Was ist mit Beugung und Doppelspaltinterferenz? Erwartung für Teilchen: Schatten! 5. Das Photon: Welle und Teilchen 5.5. Licht als Welle und Teilchen Ein Experiment in dem man Wellen und Teilchencharakter gleichzeitig sieht! Interferenzexperiment mit einem “Photonendetektor” Einzelphotonendetektor Teilchennachweis Helligkeitschwankungen Welleninterferenz! Reduziere Intensität auf einzelne Photonen/sec nette Animation, die die statistische Interpretation anschaulich macht 5. Das Photon: Welle und Teilchen Wellenbild ergibt Blaue Linie: Wahrscheinlichkeits verteilung der Photonen Einzelne Photonen Verbindung von Wellen und Teilchenbeschreibung: Photonen: Photonendichte = Intensität/ (c h ν) Ebene Welle: Elektrische Feldstärke ∝ cos(ν/2π t) Intensität ∝ E2 Wahrscheinlichkeit für ein Photon zu finden ∝ Quadrat der Amplitude 5. Das Photon: Welle und Teilchen Wellenbild ergibt Blaue Linie: Wahrscheinlichkeits verteilung der Photonen Einzelne Photonen •Wellenbeschreibung gibt die “Wahrscheilichkeitsverteilung” •Keine Aussage wo das nächste Photon auftaucht •Einteilcheninterferenz: bleibt erhalten wenn man die Intensität herabsetzt 5. Das Photon: Welle und Teilchen Teilchencharakter Photoelektrische Effekt Compton Effekt Hohlraumstrahlung Wellencharakter Elektromagnetische Welle: Maxwellgleichung Hertz: Übertragung Interferenz 1) Photonen einzel nachweisbar (was interferiert?) 2) Teilchen -> welchen Weg? ? rr i ( k ⋅r −ωt ) WELLE e Frequenz ν Kreisfrequenz ω=2πν Wellenlänge λ Wellenzahl k = 2π/λ Dispersionsrelation: ω = ck 5. Das Photon: Welle und Teilchen Lösung: •Photonen kann man an einem Ort nachweisen (Beweis: Detektorbild) •Photonen haben einen Impuls (Richtung) (Beweis: Comptonstreuung) => in der klassichen Physik: Teilchen bewegen sich auf einer Bahn im Phasenraum Quantenmechanisch: Ort und Impuls nicht gleichzeitig – keine Bahn! QM: Heisenbergsche Unschärferelation Δx Δpx ≥ ħ 6. Teilchen als Wellen 1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900 5.2. Der Photoelektrische Effekt - Beobachtungen - Einsteins Interpretation - Impuls und Energieerhaltung 5.3. Der Comptoneffekt 5.4. Die Plancksche Strahlungformel 5.5. Licht als Welle und Teilchen 6. Teilchen als Welle (de Broglie) 7. Heisenbergsche Unschärferelation 8. Das Bohrsche Atomodell 9. Grundlagen der Quantenmechanik 10. Quantenmechanik des Wasserstoffatoms 11. Spin und Bahnmagnetismus 12. Atome im Magnetfeld 13 Experimente zur Drehimpulsquantisierung 6. Teilchen als Wellen Louis de Broglie had the boldness to maintain that not all the properties of matter can be explained by the theory that it consists of corpuscles (C.W. Oseen bei der Würdigung de Broglies zur Verleihung des Nobelpreises) 1924: De Broglie Wellenlänge eines Teilchens mit Masse m0: λ = h/p = h/ √2m0Ekin Einstein (1905), Annalen der Physik 17, 132: für Photonen 6. Teilchen als Wellen 6. Teilchen als Wellen Licht als: WELLE De Broglie e rr i ( k ⋅r −ωt ) TEILCHEN (Ruhemasse = 0) Frequenz ν Kreisfrequenz ω Energie E = hν = ћω Wellenlänge λ Wellenzahl k = 2π/λ Wellenvektor k Impuls p = E/c Dispersionsrelation: Energie-Impuls-Beziehung: ω = ck E = cp = hν/c = h/λ = ћk p= ћk, λ=h/p TEILCHEN (Ruhemasse =m) Energiekin = 1/(2m) p2 λ = h/p = h/ √2m Ekin Energie-Impuls-Beziehung: E = 1/(2m) p2 6. Teilchen als Wellen 1924: De Broglie Wellenlänge eines Teilchens: λ = h/p = h/ √2m0Ekin Beispiel 1: Beispiel 2: 100 g Ball, 100 km/h Elektron 100eV 2*10-34 m 1.2*10-10 m vgl: Atom 10-10 m, Kern 10-15m 6. Teilchen als Wellen 1. Einführung 1.1. Quantenmechanik – versus klassische Theorien 1.2. Historischer Rückblick 2. Kann man Atome sehen? Größe des Atoms 3. Weitere Eigenschaften von Atomen: Masse, Isotopie 4. Atomkern und Hülle: das Rutherfordexperiment 5. Das Photon: Welle und Teilchen 5.1. Welle vs. Teilchen vor 1900 5.2. Der Photoelektrische Effekt - Beobachtungen - Einsteins Interpretation - Impuls und Energieerhaltung 5.3. Der Comptoneffekt 5.4. Die Plancksche Strahlungformel 5.5. Licht als Welle und Teilchen 6. Teilchen als Welle (de Broglie) 6.1. Die deBroglie Wellenlänge 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment 6.3. Möllenstedt-Düker Experiment 6.4. Experimente 3: Atome/Moleküle als Welle 6. Teilchen als Wellen 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment Zur Erinnerung: Röntgenstrahlen an Kristall Bragg Reflektion : d d*sin(α) Bragg Bedingung für konstruktive Interferenz: 2d sin(α) = m * λ Wellenlänge Gitterabstand Ganze Zahl 6. Teilchen als Wellen 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment Heizdraht (Elektronenquelle) Spannung -> Elektronenenergie Nickel Oberfläche Elektronennachweis 6. Teilchen als Wellen 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment Bragg Reflektion von Elektronen: 6. Teilchen als Wellen 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment Vakuumröhre •Nickeloberfläche muss “gut” sein •Vakuum für Elektronenausbreitung 6. Teilchen als Wellen 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment 6. Teilchen als Wellen 6.2. Experimente 1: Elektronen als Welle Davisson Germer Experiment 6. Teilchen als Wellen 6.2. Experimente 1: Davisson Germer (1927) 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Ein Doppelspaltversuch mit Elektronen Echter Doppelspalt schwierig: Elektron 100eV 1.2*10-10 m 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Ein Doppelspaltversuch mit Elektronen Fresnel Biprisma reale Lichtquelle 2 kohärente Virtuelle Lichtquellen 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Analogon zum Doppelspalt reale Lichtquelle 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Elektronenquelle Faden+ 0.001 mm! - - Film •Extrem vibrationsarmer Aufbau •Sehr lokalisierte Elektronenquelle 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Zeit 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Particles (electrons or ions) which are emitted from a sharp tungsten tip (right) may pass a thin wire either on the left or right hand side. By applying a voltage to the wire the two beam parts overlap and interfere (left Keine Spannung: Schatten mit Beugung an Kante Mit Spannung: Interferenz http://www.ati.ac.at/~summweb/ifm/main.html 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Möllenstedt/Düker (1956): Doppelspalt mit Elektronen Jönsson: echter Doppelspalt 1961 Claus Jönsson (Tübingen) Zeitschrift für Physik 161 454 Möllenstedt&Düker ca 0.01mm kohärent ausgeleuchtet Jönsson: 0.001 mm Spaltbreite hergestellt (galvanisch) 6. Teilchen als Wellen 6.3. Experimente 2: Möllenstedt/Düker Experiment (1956) Interferenz von Teilchen Möllenstedt/Düker (1956): Doppelspalt mit Elektronen Jönsson: echter Doppelspalt 1961 50keV (Wellenlänge: 5*10-12m) Entspricht Lichtoptik Wellenlänge 105 größer, 5cm Spalt, 20cm Spaltabstand, 40km Quelle-Spalt Spalt-Schirm (geht nicht wegen Intensität) 6. Teilchen als Wellen 6.4. Experimente 3: Atome und Moleküle als Wellen Eintrittsschlitz 2μm He* inkohärent λ= 0.47 Å 1μm 8μm •angeregtes Helium zum einfacheren Nachweis •Wellenlänge (i.e. Geschwindigkeit) muss “scharf” sein •Schlitze!! Carnal&Mlynek, PRL 66,2689)1991 Graphik: Kurtsiefer&Pfau 6. Teilchen als Wellen 6.4. Experimente 3: Atome und Moleküle als Wellen Eintrittsschlitz 2μm He* inkohärent λ= 0.47 Å 1μm 8μm Wellenlänge < Radius! Carnal&Mlynek, PRL 66,2689)1991 Graphik: Kurtsiefer&Pfau 6. Teilchen als Wellen T. Pfau, ETH Zürich 6. Teilchen als Wellen Doppelspaltexperiment mit Fullerenen (C60) λdeBroglie = 25 Angstrom Prof. Markus Arndt, Wien http://homepage.univie.ac.at/Markus.Arndt/ 6. Teilchen als Wellen Was geschieht wenn man hinter dem Spalt „hinschaut“ um den Weg zu bestimmen? Trick: Erhitzen der Fulleren, sodaß sie „leuchten“ (themische Strahlung aussenden). λdeBroglie = 25 Angstrom Prof. Markus Arndt, Wien http://homepage.univie.ac.at/Markus.Arndt/ 6. Teilchen als Wellen Interferenzbild als Funktion der Temperatur, d.h. der Anzahl der Photonen die entlang des Weges ausgesandt werden Nature 427, 711–714 (2004).