Hyper-fine structure - Fakult at f ur Physik

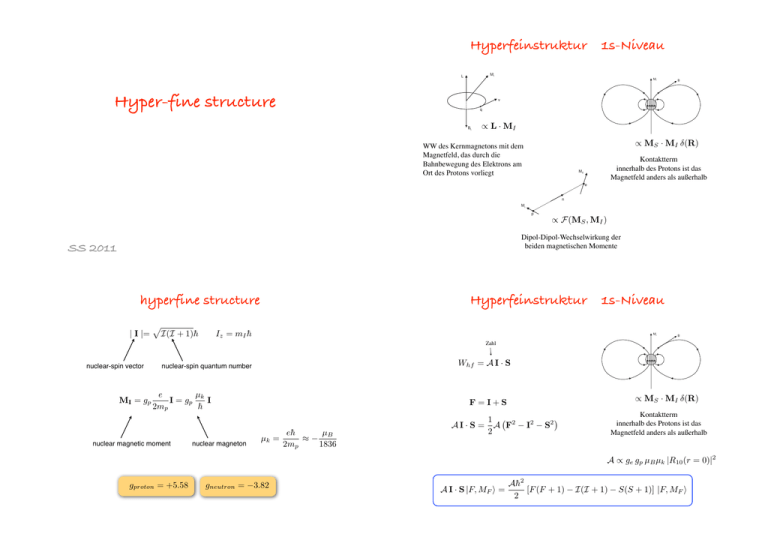
Hyperfeinstruktur
"
!
1s-Niveau
#
!
Hyper-fine structure
"
#
$
%
&
!
∝ L · MI
∝ MS · MI δ(R)
WW des Kernmagnetons mit dem
Magnetfeld, das durch die
Bahnbewegung des Elektrons am
Ort des Protons vorliegt
!
Kontaktterm
innerhalb des Protons ist das
Magnetfeld anders als außerhalb
&
%
$
!
"
#
∝ F(MS , MI )
SS 2011
Dipol-Dipol-Wechselwirkung der
beiden magnetischen Momente
Hanspeter Helm
hyperfine structure
| I |=
!
I(I + 1)h̄
Hyperfeinstruktur
Iz = mI h̄
1s-Niveau
!
"
#
Zahl
nuclear-spin vector
MI = gp
Whf = A I · S
nuclear-spin quantum number
e
µk
I = gp
I
2mp
�
nuclear magnetic moment
nuclear magneton
∝ MS · MI δ(R)
F=I+S
µk =
eh̄
µB
≈−
2mp
1836
AI · S =
"
1 ! 2
A F − I2 − S2
2
Kontaktterm
innerhalb des Protons ist das
Magnetfeld anders als außerhalb
A ∝ ge gp µB µk |R10 (r = 0)|2
gproton = +5.58
gneutron = −3.82
A I · S |F, MF ! =
Ah̄2
[F (F + 1) − I(I + 1) − S(S + 1)] |F, MF !
2
Hyperfeinstruktur
1s-Niveau
Hyperfeinstruktur
wir betrachten den Zustand
wir betrachten den Zustand
!
|s = 1/2, I = 1/2; F, MF !
+
Ah̄2
4
3Ah̄
−
4
"
+
∝ MS · MI δ(R)
2
bei F = 0 ,
|s = 1/2, I = 1/2; F, MF !
#
MF = 0, ±1
bei F = 1 ,
1s-Niveau
MF = 0
Kontaktterm
innerhalb des Protons ist
das Magnetfeld anders als
außerhalb
Ah̄2 = 1.420405751768 GHz
Ah̄2
4
3Ah̄
−
4
!!
bei F = 1 ,
" #$
)
" #$
% & ' ( #
)
* +#
MF = 0, ±1
6 #0 #,
, ! 2
- α.
2
bei F = 0 ,
/ #0 #,
MF = 0
' #, 25 "
, 1
, 2.
!#4 25 "
Ah̄2 = 1.420405751768 GHz
/ #0 #3
A I · S |F, MF ! =
Ah̄2
[F (F + 1) − I(I + 1) − S(S + 1)] |F, MF !
2
Bisherige Korrekturen:
Wasserstoff Maser (Atomuhr)
Radioastronomie 21-cm Linie
Zeeman-Effekt + Hyperfeinstruktur
!
! " % $*
! " % $)
! " % $(
! $% $'
& "
' "
& #
' #
& $
' $
& %
0
*
! $% $&
! $% $'
4p
( "
! $% $(
( #
!0.1
3p
!
"
h̄2 2
−
∇ + V (r) ϕ("r) = E ϕ("r)
2µ
E
!=1
!0.2
2p
0
5
10 15 20 25 30
r
ϕ(r, θ, φ) = Rn� (r) · Y�m (θ, φ)
Gesamtdrehimpuls
F=L+S+I
Gesamtes magnetisches Moment
!!
" #$
)
" #$
% & ' ( #
)
* +#
MF = M! + MS + MI
) "
6 #0 #,
! $% $)
"!
#
Wmv
p4
=− 3 2
8me c
h̄4
!Wmv " = − 3 2
8me c
!
, ! 2
- α.
Magnetische Energie
ϕ∗n!m ∇4 ϕn!m dV
/ #0 #,
WZ = −B0 (M! + MS + MI )
' #, 25 "
, 1
, 2.
2
!WD " ∝ |Ψ(r = 0)|
WSB =
e2 1
L·S
m2e c2 r3
Whf = A I · S
!#4 25 "
J=L+S
= ω0 (Lz + 2Sz ) + ωk Iz
/ #0 #3
ωk ! ωL
F=I+S
= 0 für H(1s)
sehr klein
W1s = A I · S + 2ω0 Sz
Zeeman-Effekt im H(1s)
Hamiltonian in der |F MF ! Basis
|F MF !
|0 0! =
!
|1 0! =
!
1
| + −! −
2
1
| + −! +
2
!
|F MF !
1
| − +!
2
!
1
| − +!
2
!!
" #$
)
" #$
% & ' ( #
)
* +#
|1 + 1!
|1 − 1!
|1 0!
|0 0!
|1 + 1!
Ah̄2 /4 + h̄ω0
0
0
0
|1 − 1!
0
Ah̄2 /4 − h̄ω0
0
0
|1 0!
0
0
Ah̄2 /4
|0 0!
0
0
−h̄ω0
6 #0 #,
|1 + 1! = | + +!
, ! 2
- α.
/ #0 #,
|1 − 1" = | − −"
' #, 25 "
a
b
2
1
ali
on
g
a
di
−h̄ω0
n
e
2
r
sie −3Ah̄ /4
1, �1
, 1
, 2.
1, 0�
1, �1
1, 0
1, �1
!#4 25 "
/ #0 #3
1
0
F, MF
GHz
GHz
Singlett , Triplett
0
F, MF
�1
�1
|mI mS ! = | ± ±!
W1s = A I · S + 2ω0 Sz
0.
0.005
0.01
Tesla
Zeeman-Effekt im H(1s)
1, �1
0, 0
�2
0.
0, 0�
0.05
0.1
Tesla
W1s = A I · S + 2ω0 Sz
Hamiltonian in der |F MF ! Basis
|F MF !
!
|0 0! =
|1 0! =
1
| + −! −
2
!
1
| + −! +
2
!
1
| − +!
2
!
2ω0 Sz |0 0!
1
| − +!
2
|1 + 1! = | + +!
#
1
| − +!
= 2ω0 Sz
2
!"
#
"
1
1
= −h̄ω0
| + −! +
| − +!
2
2
!"
1
| + −! −
2
"
= −h̄ω0 |1 0!
(1)
|1 − 1" = | − −"
Singlett , Triplett
|mI mS ! = | ± ±!
W1s = A I · S + 2ω0 Sz
1
E(MF = +1) = + Ah̄2 + h̄ω0
4
1
E(MF = −1) = + Ah̄2 − h̄ω0
4
!
" 2 #2
1
E(MF = 0+ ) = − Ah̄2 +
Ah̄ /2 + (h̄ω0 )2
4
!
" 2 #2
1
E(MF = 0− ) = − Ah̄2 −
Ah̄ /2 + (h̄ω0 )2
4
W1s = A I · S + 2ω0 Sz
Aufspaltung im Magnetfeld
Schicksal der MF Zustände
2
1, �1
1, 0
1, �1
F, MF
1, �1
1
10
28 GHz/T
0
F, MF
�1
�1
0
0.005
�1
Tesla
1, �1
high-field seekers
�, �
�, �
0, 0�
0.05
F, MF
�10
1, �1
�2
0.
0.01
0
m I , mS
0, 0
0.
1
beim Eintritt in ein
inhomogenes
Magnetfeld:
�, �
�, �
GHz
0
20
low-field seekers
1, 0�
c
1, 0�
GHz
GHz
← 1.42 GHz →
Ah̄2 =
1
1, �1
b
GHz
a
b
2
Paschen-Back Effekt
�20
0
0.1
0.5
0, 0�
�2
0.
0.05
1.
0.1
Tesla
Tesla
Tesla
−µs B0 = 2ωL Sz
damit ist eine räumliche Trennung der MF Zustände möglich !
1
AI · S = A(F2 − I2 − S2 )
2
W1s = A I · S + 2ω0 Sz
Entkopplung im Vektormodell
a
F, MF
�1
GHz
GHz
0
0
m I , mS
�2
0.
0.01
Tesla
0.05
1, �1
�10
0, 0�
�20
0
0.1
1 23 24
*
5
�, �
�, �
0, 0
0.005
+ # , ( $ - .( /
10
% & ' ( ) 1 23 27
F, MF
b
2
0.5
23 24 67
1, �1
Tesla
Tesla
1
1 23 27
! "# $
1.
1, 0�
Quarzkugel,
Teflon beschichtet
!
1
!
0 $ .# $ $ #
"
#
"
#
GHz
0.
Kleppner und Ramsey (1961-71)
�, �
�, �
1
0
�1
c
20
1, �1
1, 0�
1, �1
1, 0
1, �1
GHz
b
2
1
Wasserstoff - Maser
$
%
8
0
F, MF
�1
1, �1
9
◉
8
8
%
9
Paschen-Back Effekt
$
&
�
�2
0.
0, 0
0.05
0.1
Tesla
∆ν/ν = 10−15 pro Tag
9
µe
ge µB
=
= −658.21 . . . ..
µp
gp µk
Wasserstoff - Maser
Phase-locked loop
(PLL)
4-bit
counter (up)
add
D/A
4-bit
counter (down)
PTB - Braunschweig
harmonische Schwingung wird in
digitales Signal konvertiert
Active frequency standard
←tuned, resonant cavity
storage bulb
H-atom source
a self-sustaining microwave field builds up in the bulb
the active microwave signal is compared with that of a quartz oscillator
the quartz oscillator is phase-locked to the H-signal
http://tf.nist.gov/general/enc-h.htm#hydrogenmaser
18
Previdelli et al. Appl. Phys. B 60 S241 (1995)
Regelsignal mit
Vorzeichen !
phase gap increases
19
Lamb-Retherford experiment
and
QED effects
SS 2011
Hanspeter Helm
Williams Physical Review A 54 558 (1938)
Fine structure in atomic hydrogen
3
! "# %& '
(%# "*
! "# $ %& '
+ 0
(#
(#
! "! + %& '
+ ,
+ -.
# -.
+ ,
+ /
* -.
+ /
+ -.
1 %2 %+
# -.
1938: Houston und Williams beoachten Abweichungen der
Position der Hα -Linie von der Position, die von der
Dirac-Theorie vorhergesagt wird.
1 %2 %.
(%+ ")
! ") * %& '
(#
! "+ %& '
. 0
# -.
. ,
+ -.
. ,
# -.
(#
Pasternak (1938 ) : diese Beobachtung deutet darauf hin,
dass der H(2s) Zustand um 0.03 cm-1 höher liegt
als von der Theorie vorhergesagt.
1 %2 %#
(%# + "$
# ") * %& '
4 5
(#
# 0
(#
# -.
degeneracy of terms with equal quantum numbers n and J
Wurde nicht ernst genommen, “Fehler im Experiment” vermutet
Lamb - Retherford experiment (1947)
Spin 1/2 in a magnetic field
H(2s) --> H(2p)
!
"
! #$ %& '
( )* +
! ," - .
$ + /* 0 1 + 0
! 2 #$ + /* 0 1 + 0
M = gs µB S
H(2s)
Detektion
*
!""
20
10
*
GHz
3
#
0
!!"
!10
!20
1 in 108 H-atoms is excited
by electron impact :
H(1S) + e " H(2s) + e
0
lifetime of H(2s)
t = 1/7 s
lifetime of H(2p)
t = 1.6 ns
0.5
1
Tesla
1.5
2
orbital angular momentum L = 1
in a magnetic field
J= 3/2
Landé factor
!
$
S = 1/2 "
#
#
!
! - . +,
+
! * +,
"
M = µB L
)
! "
!
#
(
!
#
*# +
+
#
MJ · J
!MJ " =
|J|
! )
L= 1
"
)
! )
%
#
!WZ " = µB B MJ gJ
!
) ! * +,
# $
#
% &' &(
(
(
Mges = µB (L + gs S)
+
%
"
& '%
'(
$
% &' &(
%
gJ-factor is always
between 0 and 2
J=L+S
$
|n, !, mL !
Multiplett splitting
J= 3/2
Lamb - Retherford
S = 1/2
J=L+S
�
!
|J| = J(J + 1)
√
ML
!WZ " = µB B MJ gJ
3/4
√
2
fine structure
& ' (%
L= 1
& $ (%
$ %
2
% +
! 7
! )+ , -
' (%
)$ (%
% )!
01
2 3
4 3% )! 6
% &
#
S
+L
→
J
=
=
−
=
1/2
1
�
2 3/4
Ms
$
)' (%
#
& $ (%
& $ (%
)$ (%
"
"
% ,
% +
$ (%
$ (%
!
/ )!
01
2 3
4 35% )! 6
! .
% )!
01
2 3
4 35% )! 6
! .
!
%
)$ (%
& '%
$
1/2, 3/2
! .
-. / 0 1
*
%
& '!
'
Lamb shift
( )*
% )!
01
2 3
4 3% )! 6
Kraftfelder
Descartes : Trägheitsgesetz
● Kraft kommt durch den unmittelbaren Kontakt
! zwischen Körpern zustande
● Raum ist gefüllt mit einer Substanz,
! welche die Kraft übermittelt
A simple man’s view
of
QED
Newton : Wechselwirkung zwischen
massebehafteten Teilchen (Symmetrie
zwischen sich anziehenden Objekten)
(Quantum Electro-Dynamics)
Niemand hinterfragte die instantane Kraftübertragung
Maxwell : Wellenausbreitung mit Lichtgeschwindigkeit
Welche Substanz trägt die Wellenbewegung (macht sie mit)?
Michelson & Moreley suchen nach dem Äther
more precise experiments show:
1) a small deviation of the g-factors of the electron from g=2
Invarianz der Lichtgeschwindigkeit
Michelson & Morely Experiment erfordert drastische
Revision des klassischen Konzepts von Raum und Zeit.
Einstein fand einen Weg Geschwindigkeiten zu addieren, ohne
dass die Konstanz der Lichtgeschwindigkeit verletzt wird.
"
α
− O(α2 )
ge = 2.0023 = 2 1 +
2π
!
c+v =c
2) Lamb shift
V = (v1 + v2 )/(1 + v1 v2 /c2 )
0
Man muss die Idee aufgeben,
dass man Raum und Zeit unabhängig messen kann
!"$ %(
' %( ) "* +
!#
' %$ "* +
, /
# .,
3 "' %' $ "* +
!#
3 "' %, 4 "* +
!#
!"# $ %&
# %( ) "* +
1 2
# /
!#
# .,
, -
$ .,
, -
# .,
!#
• Es gibt keine universelle Zeit.
• c ist ein absolutes Maximum,
• Masse und Energie sind essenziell dasselbe.
Quantisierung
Raum - Zeit Diagramm
Die Steigung c kann nicht überschritten werden.
Wohin geht die Energie, wenn das Teilchen doch nicht schneller wird?*
! " # $%$" & '(
* Masse nimmt zu
1) Wirkung einer Kraft kann sich an einem gegebenen
! Raum-Zeit-Punkt nicht kontinuierlich verändern
2) Die Ganzheit, welche die Kraftwirkung verursacht,
! ist ein Quant
3) Kraftfelder werden aus Quanten aufgebaut
%$) * '%
Auch der Informationstransport “Kraft” unterliegt der Grenze der
Lichtgeschwindigkeit.
Es muss einen Boten geben, der die Kraftinformation befördert.
Diesen Boten bezeichnet man als Feld.
Kraftfelder
Klassisch :
An jedem Punkt der Raum-Zeit gibt es eine Markierung für die Stärke der Kraft
4) Quanten werden zwischen den Teilchen,
! die eine Kraft erfahren, ausgetauscht
Kraftfelder
Kraft kann als Emission plus Absorption eines
Feldquants angesehen werden.
Sender und Empfänger des Quants sind vertauschbar,
ohne dass sich die Kraftwirkung ändert.
Auf Grund der Relativität muss die Kraft für eine
gewisse Zeit unterwegs sein.
QM:
es gibt nur eine Markierung der Wahrscheinlichkeit, dass der Empfänger
der Kraft eine diskrete Kraftwirkung erleidet
Bild aus dem Buch: ”The force of symmetry” von V. Icke (Cambridge Univ. Press, 1995).
Auf Grund des Quantenverhaltens muss die Kraft
durch diskrete Quanten übertragen werden.
Feynman Diagramme 1. Ordnung
Bild für eine abstoßende Kraft
! "# $
Das virtuelle Quant wird durch
die Wellenlinie dargestellt.
$
$
!
Die geraden Linien
repräsentieren z.B. zwei
Elektronen.
$
$
% & ' ( $
Zwei (reibungsfreie) Eisläufer, einer wirft dem anderen einen
Medizinball zu. Ein entfernter Beobachter sieht den Ball nicht,
stellt aber fest, dass sich die beiden Eisläufer abstoßen.
Ein Elektron besitzt keine inneren Freiheitsgrade zur Energiespeicherung.
Bei der Emission des virtuellen Quants wird der Energiesatz vorübergehend
verletzt. Nach Absorption des Quants durch das andere Elektron, stimmt aber der
Energiesatz.
Quanten
Feynman Diagramme
beschreiben den Austausch von Quanten in einer zweidimensionalen Darstellung.
Eine der drei räumlichen Dimensionen wird gegen die Zeit aufgetragen
! "# $
$
$
!
$
Die Energie des ausgetauschten
Quants ist eine kontinuierliche
Variable
(sie kann im Prinzip beliebig
groß sein).
$
% & ' ( $
Das Feldquant ist einer direkten Beobachtung nicht zugänglich
( virtuelles Quant )
Würden wir es beobachten, dann würden wir den Krafteffekt unterbinden.
elektrische
Name
Symbol
Spin
Ladung
Photon
γ
1
0
(Schwaches Photon)
W +, Z 0, W −
1
1,0,-1
Gluon
g
1
0
2
0
Graviton
Elektron
e
1
2
-1
Neutrino
ν
1
2
0
Proton
p
1
2
1
Neutron
n
1
2
0
Quantenfeldtheorie
Quanten-Elektrodynamik
Beschreibt die WW zwischen elektrisch geladenen Teilchen und Photonen.
Die Quantenfeldtheorie beschreibt alle Teilchen durch Felder.
So wie sich das elektromagnetische Feld durch Photonen zu erkennen gibt,
gehören Elektronen oder Protonen zum Elektronenfeld bzw. Protonenfeld.
Einer einzelnen Elektronenwellenfunktion entspricht eine gewisse
Frequenzanregung des Elektronenfeldes.
Je nach der Wechselwirkung dieser Anregung mit der Umgebung kann man
das Elektron mehr oder weniger lokalisieren.
Quantenfeldtheorie
Mathematisch:
Quantenfeld besteht aus unendlich vielen harmonischen Oszillatoren.
Anregung mit einer gegebenen Frequenz entspricht einem
Teilchen mit diskretem Impuls (einem Feldquant)
Die elektromagnetische WW (Coulombkraft) kommt durch die Absorption und
Emission von Quanten zustande (Austauschkraft)
Ursprünglich: QED erklärt
Emission und Absorption von Lichtquanten bei atomaren Übergängen.
Lamb shift : man muss annehmen, dass ein freies, wie auch ein gebundenes
Elektron ständig Lichtquanten emittiert und wieder absorbiert.
Schwinger, Feynman
& Tomonaga 1948
Quantum electrodynamics is a generalization of quantum dynamics to
include special relativity.
The Nobel Prize in Physics 1965
"for their fundamental work in quantum electrodynamics,
with deep-ploughing consequences for the physics of elementary particles"
Bosonenfelder : keine Beschränkung der Anzahl von Quanten in einem
gegebenen Energiezustand. Große Mengen von Photonen können sich
kohärent überlagern und makroskopische Wirkungen erzielen.
Auf Grund des Pauli-Verbotes ist die Wirkung eines Fermionenfeldes
weniger auffällig.
Regeln für Feynman - Graphen
Virtuelle Prozesse
Vertex:
Ein Punkt an dem drei oder mehrere
Teilchen zusammentreffen.
!
!
Während einer kurzen Zeitspanne leiht sich das Elektron vom
Coulombfeld Energie und emittiert diese als Photon.
!
"
!
!
Jedem Vertex entspricht im
Übergangsmatrixelement ein Faktor,
der die Struktur und Stärke der
Wechselwirkung enthält.
!
Kurze Zeit später wird dieses Photon vom Elektron selbst oder
von einem anderen Teilchen, das elektrische Ladung besitzt,
wieder absorbiert.
!
!
!
!
!
!
!
!
!
Dieser Faktor ist proportional zu "#
!
Feynman - Graphen
Regeln für Feynman - Graphen
das Leben
! "# $
*
*
)
eines Elektrons:
)
"
!
"
"
"
+
###
eines Photons:
+
,
$% &
!
"
"
"
% & ' ( $
Das Endergebnis ist
ununterscheidbar.
! "# $
*
$' &
,
% & ' ( $
! "# $
(
Zwei Möglichkeiten, dass zwei
Elektronen
von 1 und 2 nach 3 und 4 gehen.
! "# $
)
*
)
-
.
Zwei andere Möglichkeiten dafür.
.
-
)
+
+
,
,
% & ' ( $
% & ' ( $
Das Endergebnis ist
ununterscheidbar vom Fall oben.
Elektron im H-Atom
! "# $
& )* +* ,
$ -$ ( +) * ,
Proton und Elektron tauschen
Photonen aus.
Das schwere Proton ist praktisch
Lamb Verschiebung
Selbst bei Abwesenheit äußerer Felder muss die Anwesenheit eines
fluktuierenden elektromagentischen Feldes im Raum angenommen werden
Diese virtuelle Wechselwirkung führt zu einer winzigen
Energieverschiebung.
stationär und hält das Elektron auf
einer zittrigen Bahn fest.
% & ' ( $
Vakuumpolarisation :
Wenn das Austauschquant ein Elektron-Positron Paar bildet,
ist der Effekt eine Reduktion der effektiven Ladung.
Die Energieverschiebung hängt ab von der Aufenthalts-Wahrscheinlichkeit
des Elektrons in Kernnähe
Die Korrektur ist so klein, dass sie nur in sehr präzisen Messungen erfasst
werden kann.
Quanten - Vakuum
klassischen Physik : leere Raum-Zeit = Vakuum
Quantenmechanik : Vakuum = Grundzustand des Quantenfeldes
Lamb Shift
Anschauliches Bild:
Elektron auf einer zittrigen Bahn
Das Vakuumfeld enthält keine angeregten Feldquanten, also
keine Teilchen und stellt den Zustand minimalster Energie dar
!
0
Analogie:
Quantenfeld und unendliche Anzahl von harmonischen Oszillatoren
!
"
1
)
r + δr
1
r + δr
"
! "
1
!
=
r
!"$ %(
' %( ) "* +
!#
' %$ "* +
, /
Nullpunktsfluktuationen müssen angenommen werden.
An diesen Fluktuationen sind nur virtuelle Teilchen beteiligt.
Ständig entstehen aus dem Vakuum Teilchen-Antiteilchen-Paare, sie
propagieren solange es die Unschärferelation erlaubt und dann
annihilieren sie.
Ze2
4π"0
!Epot " = −
# .,
3 "' %' $ "* +
, -
$ .,
, -
# .,
!#
n!
!#
!"# $ %&
# %( ) "* +
1 2
# /
!#
# .,
3 "' %, 4 "* +
mv+D
!#
0.03
Lamb HFS
cm-1
1s
2s
2p
∆Elamb
M Hz
+8000
+1040
−14
∆Elamb
cm−1
+0.267
+0.034
−0.005