Die Turingmaschine besteht aus • der Steuereinheit, die

Die Turingmaschine besteht aus
• der Steuereinheit, die verschiedene Zustände annimmt
• dem Band, welches unendlich ausgedehnt ist, aber nur auf
einem endlichem Bereich mit Zeichen aus einem Alphabet
beschrieben ist
• dem Lese-Schreib-Kopf
• der Übergangstabelle
In jedem Verarbeitungsschritt:
• wird das Zeichen unter dem Lese-Schreib-Kopf gelesen
• wird in der Übergangstabelle nach dem Eintrag gesucht, der
dieses Zeichen und den aktuellen Zustand der Steuereinheit
enthält,
• werden Zeichen und Zustand entsprechend der Angaben in
der Übergangstabelle geändert und
• wird der Lese-Schreib-Kopf um eine Position nach links (L)
oder rechts (R) weiterbewegt. Auch dies wird in der Übergangstabelle festgelegt.
• Der Lese-Schreib-Kopf kann auch angehalten werden (H). Die
Verarbeitung ist dann beendet.
257
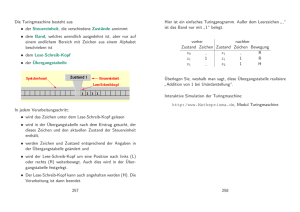
Hier ist ein einfaches Turingprogramm. Außer dem Leerzeichen “
”
ist das Band nur mit 1“ belegt.
”
vorher
nachher
Zustand Zeichen Zustand Zeichen Bewegung
z0
z1
R
z1
1
R
z1
1
z1
z2
1
H
Überlegen Sie, weshalb man sagt, diese Übergangstabelle realisiere
Addition von 1 bei Unärdarstellung“.
”
Interaktive Simulation der Turingmaschine:
http:/www.Matheprisma.de, Modul Turingmaschine
258
7.1.2
Grenzen der Berechenbarkeit
Es gibt Funktionen, die nicht berechenbar sind.
Wegen der Church’schen These heißt dies: die nicht mit einer
Turingmaschine berechnet werden können.
1 3 Beispiel: Halteproblem
Menge der Eingaben: alle möglichen Übergangstabellen U
von Turingmaschinen
Funktion f :
8
1 falls die Turingmaschine mit
>
>
<
Übergangstabelle U für jede
f (U ) =
Bandbelegung anhält,
>
>
:
0 sonst
Es gibt keine Übergangstabelle für eine Turingmaschine, die
f berechnet.
Den Nachweis zu dieser Aussage können wir hier nicht führen.
Die Berechnung von Funktionen, die nur die Werte 0 und 1
annehmen, nennt man auch (ja/nein)-Entscheidungen. Man sagt
deshalb: Das Halteproblem ist nicht entscheidbar.
259
2 3 Beispiel: Unentscheidbarkeit der Prädikatenlogik
Die Prädikatenlogik baut auf der Aussagenlogik auf. Prädikate enthalten Variablen; für jede Belegung der Variablen
nehmen sie den Wert wahr oder falsch an. Prädikate können
wie Aussagen verknüpft werden, zusätzlich auch mit den
Quantoren ∀ und ∃. Genaueres wird hier nicht erläutert.
Die Frage, ob eine prädikatenlogische Formel für jede Belegung der Variablen den Wert wahr annimmt, ist nicht entscheidbar.
3 3 Beispiel: Unentscheidbarkeit der Korrektheit
Die Frage, ob ein Programm semantisch korrekt ist (d.h.
es berechnet tatsächlich die spezifizierte Funktion), ist unentscheidbar.
Auch für diese Beispiele ist ein Beweis weit jenseits von dem, was
wir hier machen können.
260
7.2
Komplexitätstheorie
7.2.1
Komplexität von Algorithmen
Wie genau kann man die Laufzeit T eines Algorithmus vorhersagen?
T hängt ab
• von der jeweiligen Implementierung
• vom verwendeten Rechner
• von der jeweiligen Eingabe
• ...
Folgerung:
• T hängt insbesondere von der Größe“ n der Eingabe ab:
”
T = T (n)
Für festes n kann T (n) immer noch unterschiedlich sein.
Wir verwenden für T (n) hier stets den worst case, also die
längste Laufzeit bei festem n.
• Es ist nicht sinnvoll, T (n) zu genau bestimmen zu wollen.
• Es genügt, die Zahl der elementaren Schritte eines Algorithmus zu bestimmen.
261
4 3 Beispiele:
a) Euklidischer Algorithmus
berechnet ggT(a, b) für a, b ∈ N.
r := a mod b
solange r 6= 0
a := b
b := r
r := a mod b
ggT := b
Eingabegröße: n = max{a, b}.
Elementare Schritte: Zuweisung, Division mit Rest, Vergleich
Laufzeit: solange-Schleife
√ wird höchstens logΘ n + 1 mal
durchlaufen (Θ = ( 5 + 1)/2).
Pro Durchlauf 3 Zuweisungen, 1 Vergleich und 1 Division
mit Rest. Also
T (n) ≤ C · (2 + 5 · (logΘ n + 1)) .
262
b) Sieb des Eratosthenes
bestimmt alle Primzahlen ≤ n.
p := 2
solange p2 ≤ n
s := 2 ∗ p {Aussieben mit Zahl p}
solange s ≤ n
streiche s {markieren}
s := s + p
setze p auf nächste, nicht gestrichene Zahl
Eingabegröße: n
Elementare Schritte: Streichen (= Zugriff auf ein Feld
und Markieren), Zuweisung, Addition, Multiplikation,
Nächstes finden
Laufzeit: die innere solange-Schleife wird n/p-mal durch√
laufen, die äußere für Primzahlen ≤ n.
1
0
√
n
X
n
A.
@
T (n) ≤ C · 1 +
p
p=1, p Primzahl
263
Die t(n)-Ausdrücke will man noch vereinfachen:
5 3 Definition: Wir schreiben
T (n) = O(g(n))
mit einer Funktion g : N → R+, falls eine Konstante C > 0
und ein n0 existieren, so dass gilt
T (n) ≤ C · g(n) für alle n ≥ n0.
6 3 Beispiele:
a) Euklidischer Algorithmus:
T (n) ≤ C · (2 + 5 · (logΘ n + 1)) .
ergibt
T (n) = O(log n).
(Wegen loga n = logb n · loga b braucht man die Basis des
log in O-Termen nicht anzugeben!)
264
b) Sieb des Eratosthenes:
0
√
n
1
T (n) ≤ C · @1 +
n
A.
p
p=1, p Primzahl
√
√
X
Es gibt höchstens n Primzahlen ≤
alle solchen Primzahlen p. Also
T (n) = O(n ·
n, und
n
p
≤ n für
√
n).
(O-Terme können sehr grob nach oben abschätzen.)
265
7.2.2
Probleme und Instanzen
7 3 Definition: Ein Problem ist eine zu berechnende Funktion
P : D → W mit zugehörigem Definitionsbereich D und
Werten in W .
Eine Instanz eines Problems P : D → W ist ein Paar
(P, S) mit S ∈ D.
8 3 Beispiele:
a) Problem größter gemeinsamer Teiler“:
”
P :N×N→N
Instanz: (a, b) = (144, 54).
b) Problem Primzahlen ≤ n “:
”
P : N → Potenzmenge von N
Instanz: n = 100
266
c)
Problem des Handlungsreisenden“:
”
P : {L : L ist Liste von Städten mit Entfernungen} →
R+
P (L) ist die Länge der kürzesten Rundtour, die alle Städte
einmal besucht.
W
RS
Instanz: L = SG
K
E
DO
d)
W
0
15
20
50
35
40
RS
15
0
10
45
50
50
SG
20
10
0
35
55
60
K
50
45
35
0
80
100
E
35
50
55
80
0
20
DO
40
50
60
100
20
0
Teilsummenproblem“:
”
P : {M : M ist eine Menge reeller Zahlen}×R → {0, 1}.
P (M, s) gibt an, ob es eine Teilmenge T von M gibt, bei
der die Summe der Elemente gerade s ergibt.
Instanz: M = {−0.2, 1, 2.3, 4.5}, s = 3.1.
267
7.2.3
Komplexität von Problemen
Wir werden jetzt Probleme in einfache“ und schwierige“ einteilen.
”
”
Ein tragfähiges Konzept hierzu ist überraschend komplex.
Ab jetzt schränken wir uns auf Entscheidungsprobleme ein, also
P : D → {0, 1}.
Als Größe n einer Eingabe S ∈ D verwenden wir die Anzahl der
bits bei geeigneter Binärcodierung.
9 3 Beispiel: Die Größe einer natürlichen Zahl k ist damit (Codierung als Binärzahl) n = O(log k).
Folge: Die Größe der Eingabe beim Euklidischen Algorithmus ist
n = O(log a + log b). Die Komplexität des Euklidischen Algorithmus wird O(n) statt O(log(max{a, b})).
10 3 Definition: Für ein (Entscheidungs-) Problem P : D →
W , ist die Komplexität t(n) des Problems P definiert als
die Laufzeit des besten Algorithmus, welcher P berechnet.
Hier genügt uns noch weniger als die Größenordnung O:
11 3 Definition: Die Klasse P ist die Menge aller Entscheidungsprobleme, für welche es eine Zahl k ∈ N gibt, so dass
die Komplexität des Problems O(nk ) ist.
268
P steht für polynomiale Komplexität .
Probleme aus P nennt man auch effizient berechenbar.
Warum ist P eine vernünftige Problemklasse?
• P ist weitestgehend unabhängig vom Maschinenmodell, also
davon, was man als elemtare Schritte auffasst. Wir hatten
auf den letzten Seiten — ohne es explizit zu sagen – das Random Access Memory (RAM) Modell verwendet. Verwendet man stattdessen z.B. das Modell der Turingmaschine,
so ändert sich P nicht.
• P ist weitestgehend unabhängig von der gewählten Binärcodierung für die Eingabe.
• Für Probleme, die nicht in P liegen, wächst die Komplexität
superpolynomial mit n. Für die Praxis sind solche Laufzeiten
definitiv viel zu lang.
12 3 Beispiel: Das Problem Entscheide, ob k der ggT von a
”
und b ist“, liegt in P .
Begründung: Es ist n = Länge einer Binärcodierung von k,
a und b. Berechne ggT(a, b) mit dem Euklidischen Algorithmus (Laufzeit O(n)) und vergleiche das Ergebnis mit k
(Laufzeit O(log(n)). Gesamtlaufzeit
t(n) = O(n) + O(log(n)) = O(n).
269
Eine fundamentale Schwierigkeit:
• Zugehörigkeit eines Problems zu P kann man durch Angabe eines geeigneten Algorithmus nachweisen.
• Will man zeigen, dass ein Problem nicht zu P gehört,
muss man zeigen, dass keine Algorithmen mit polynomialer
Komplexität existieren. Dies ist sehr schwierig.
• Es ist noch für kein praktisch relevantes Problem gelungen zu
zeigen, dass es nicht effizient berechenbar ist.
’Nicht effizient berechenbar’ ist deshalb keine günstige Art, schwierige Probleme zu charakterisieren.
Alternative: Aus der eigenen Erfahrung wissen wir: Es ist in der
Regel wesentlich schwieriger, eine Lösung zu bestimmen als nachzuprüfen, ob ein Lösungsvorschlag tatsächlich eine Lösung ist. Dies
geht in die beiden nächsten Definitionen ein.
13 3 Definition: Gegeben ist ein Entscheidungsproblem P : D →
{0, 1} und eine Menge von Zertifikaten Z . Eine Funktion
V : D × Z → {0, 1} verifiziert P , wenn es für jede Instanz (S, P ) von P mit P (S) = 1 ein Zertifikat z = z(S)
gibt mit V (S, z) = 1, und umgekehrt aus V (S, z) = 1
stets P (S) = 1 folgt. Die Größen n bzw. m von S bzw.
z(S) müssen dabei m = O(nk ) erfüllen. (z darf höchstens
polynomial in S wachsen.)
270
14 3 Beispiel: Das Problem Entscheide, ob p ∈ N keine Prim”
zahl ist“, wird verifiziert durch die Funktion V , welche jedem
Paar (p, a) mit a ∈ {2, . . . , p} den Wert 1 zuordnet, wenn
p durch a teilbar ist und 0 sonst. Es ist also Z = {2, . . . , p}.
Ein Algorithmus für V ist die Division mit Rest mit anschließendem Test, ob der Rest 0 ist.
Für p = 5529 ist z(p) = 57 ein Zertifikat mit V (5529, 57) =
1.
Es ist leichter auszurechnen, dass 57 die Zahl 5529 teilt, als
zu zeigen, dass 5529 keine Primzahl ist.
271
15 3 Definition: Die Klasse NP besteht aus all den (Entscheidungs-) Problemen, welche von einer Funktion verifiziert werden, für die es einen Algorithmus mit polynomialer Laufzeit
gibt.
Die Bezeichnung NP kommt daher, weil man die Klasse äquivalent
charakterisieren kann als die Probleme, welche mit einem nichtdeterministischen Algorithmus in polynomialer Zeit berechnet werden
können.
16 3 Satz: P ⊆ NP
Beweis Sei P : D → {0, 1} aus P . Nehme eine beliebige
Menge als Zertifikatmenge Z und setze V : D × Z →
{0, 1} als V (S, v) = P (S). Der polynomiale Algorithmus,
welcher P berechnet, berechnet auch V . Die Eingabe z wird
dabei einfach ignoriert.
Und die größte offene Frage der Theoretischen Informatik ist nun:
Gilt P = NP ?
Die Frage ist ungeklärt, aber fast alle glauben dass die richtige
Antwort Nein heißt, u.A. wegen des folgenden Resultates.
272
17 3 Satz: Die Klasse der NP-vollständigen Probleme ist nicht
leer. Diese Klasse besteht aus all den Problemen aus NP ,
für die gilt: Liegt P in P , so ist P = NP .
• Hat man für ein NP-vollständiges Problem P gezeigt P ∈ P,
so ist P = NP . Das hat bis jetzt noch niemand geschafft.
• Glaubt man P 6= NP, so liegen NP-vollständige Probleme
also nicht in P , sind also nicht effizient berechenbar.
Merke: NP-vollständig bedeutet höchstwahrscheinlich
in der Praxis nicht mit einem Algorithmus berechen”
bar“
273
7.2.4
NP-vollständige Probleme
Die folgenden Probleme sind alle als NP-vollständig nachgewiesen.
Die Beweise können wir im Rahmen dieser Vorlesung nicht bringen.
18 3 Beispiel:
a) Das Problem des Handlungsreisenden
b) Das Teilsummenproblem
19 3 Beispiel: Das Erfüllbarkeitsproblem: Gegeben ist eine aussagenlogische Formel mit n Aussageveriabeln. Gibt es eine
Belegung der Variabeln, so dass die Formel den Wert ’true’
annimmt?
Viele andere NP-vollständige Probleme beziehen sich auf Graphen.
20 3 Definition: Ein Graph ist eine Menge von Knoten, von denen
einige durch Kanten verbunden sind.
274
Beispiel: Haus vom Nikolaus
21 3 Beispiel: Das Hamilton-Kreis-Problem: Existiert in einem
Graph ein Hamilton-Kreis, d.h. ein Rundweg über die Kanten, der jeden Knoten genau einmal besucht?
22 3 Beispiel: Das Cliquen-Problem: Gibt es eine Clique der
Größe k in einem Graphen? Eine Clique ist eine Teilmenge
von Knoten, von denen zwei verschiedene stets auf einer
gemeinsamen Kante liegen. Die Größe der Clique ist die
Anzahl ihrer Knoten.
Mehr zu Komplexität und Rechnermodellen:
−→Automaten, Sprachen, Berechenbarkeit (Master)
275