Übungsblatt 9

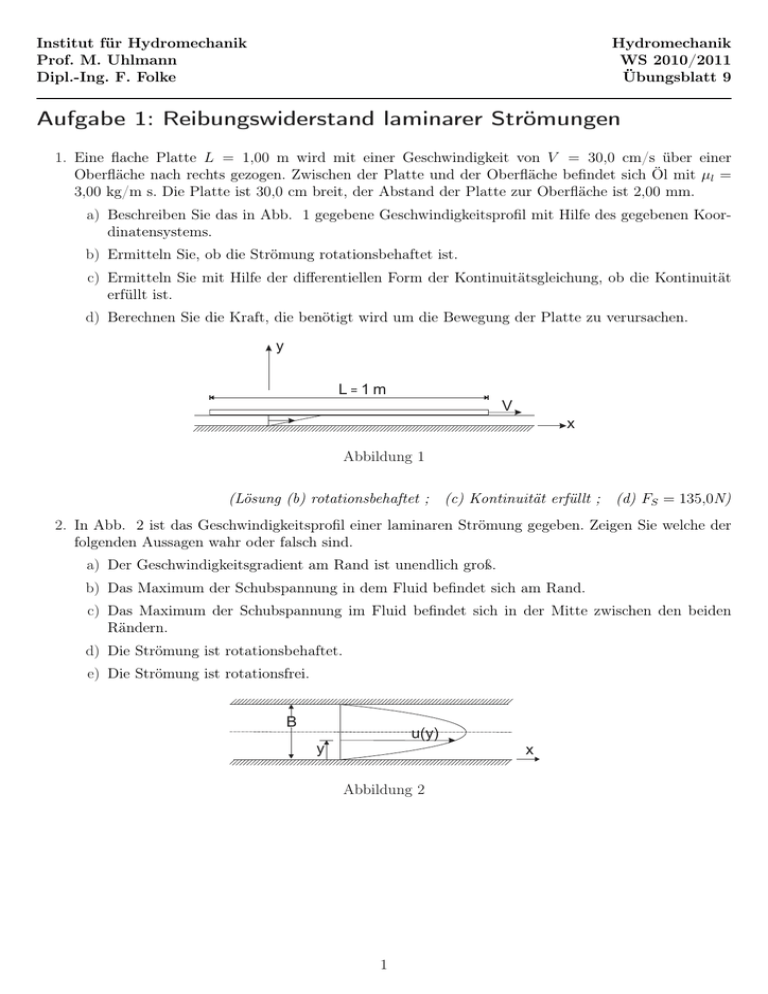
Institut für Hydromechanik
Prof. M. Uhlmann
Dipl.-Ing. F. Folke
Hydromechanik
WS 2010/2011
Übungsblatt 9
Aufgabe 1: Reibungswiderstand laminarer Strömungen
1. Eine flache Platte L = 1,00 m wird mit einer Geschwindigkeit von V = 30,0 cm/s über einer
Oberfläche nach rechts gezogen. Zwischen der Platte und der Oberfläche befindet sich Öl mit µl =
3,00 kg/m s. Die Platte ist 30,0 cm breit, der Abstand der Platte zur Oberfläche ist 2,00 mm.
a) Beschreiben Sie das in Abb. 1 gegebene Geschwindigkeitsprofil mit Hilfe des gegebenen Koordinatensystems.
b) Ermitteln Sie, ob die Strömung rotationsbehaftet ist.
c) Ermitteln Sie mit Hilfe der differentiellen Form der Kontinuitätsgleichung, ob die Kontinuität
erfüllt ist.
d) Berechnen Sie die Kraft, die benötigt wird um die Bewegung der Platte zu verursachen.
y
L=1m
V
x
Abbildung 1
(Lösung (b) rotationsbehaftet ;
(c) Kontinuität erfüllt ;
(d) FS = 135,0N)
2. In Abb. 2 ist das Geschwindigkeitsprofil einer laminaren Strömung gegeben. Zeigen Sie welche der
folgenden Aussagen wahr oder falsch sind.
a) Der Geschwindigkeitsgradient am Rand ist unendlich groß.
b) Das Maximum der Schubspannung in dem Fluid befindet sich am Rand.
c) Das Maximum der Schubspannung im Fluid befindet sich in der Mitte zwischen den beiden
Rändern.
d) Die Strömung ist rotationsbehaftet.
e) Die Strömung ist rotationsfrei.
B
u(y)
y
x
Abbildung 2
1
3. Unter gewissen Bedingungen (fallender Druck in x-Richtung und eine sich mit der Geschwindigkeit
U0 bewegende Platte) stellt sich eine laminare Geschwindigkeitsverteilung wie in Abb. 3 ein. Zeigen
Sie welche der folgenden Aussagen unter diesen Bedingungen wahr bzw. falsch sind.
a) Die größte Schubspannung des Fluids ist an der festen Platte.
b) Die Schubspannung in der Mitte der beiden Platten ist null.
c) Das Minimum der Schubspannung des Fluids ist an der sich bewegenden Platte.
d) Die Schubspannung ist dort am größten, wo die Geschwindigkeit ihr Maximum besitzt.
e) Die Schubspannung hat ihr Minimum, wo die Geschwindigkeit am größten ist.
U0
U(y)
y
x
Abbildung 3
4. Zeigen Sie, dass die mittlere Geschwindigkeit einer laminaren Strömung über ein Platte 2/3umax ist.
Aufgabe 2: Laminare / Turbulente Grenzschichten
1. Eine dünne Platte mit der Länge L = 1 m wird mit der Geschwindigkeit u = 1 m/s parallel
angeströmt (Abb. 4).
a) Berechnen Sie die Dicke der Grenzschicht an der hinteren Kante, wenn sich die Platte in einem
Ölstrom mit u = 1,00 m/s und νl = 1,00 · 10−4 m2 /s befindet.
b) An welcher Stelle x ist mit einem Übergang von laminarer zu turbulenter Strömung zu rechnen,
wenn sich die Platte in einem Wasserstrom mit u = 1,00 m/s und νwasser = 1,00 · 10−6 m2 /s
befindet?
c) Berechnen Sie die Dicke der Grenzschicht an dieser Stelle.
d) Berechnen Sie die Dicke der Grenzschicht an der Stelle x = 1 m.
e) Zeichnen Sie den Verlauf der Grenzschicht für die Fall 1 und 2!
f) Skizzieren Sie den Verlauf der lokalen Wandschubspannung entlang der Platte.
Abbildung 4
(Lösungen: (a) δ = 0,0500 m ;
(b) xcrit = 0,500 m ; (c) δcrit = 3,54 mm ; (d) δ = 23,4 mm)
2
2. Ein Flugzeug mit 10 m Spannweite und einer Flügeltiefe von 2 m fliegt 200 km/h in in Luft von 30°C.
Nehmen Sie an, dass der Widerstand der Tragflächenoberfläche dem einer flachen Platte entspricht.
a) Wie groß ist der Widerstandsbeiwert des Tragflügels?
b) Welche Kraft wird benötigt, um diesen zu überwinden?
c) Wie viel der Flügeltiefe ist laminar?
d) Wie würde sich der Widerstand ändern, wenn die Turbulenz an der Profilvorderkante ausgelöst
würde?
(Lösungen: (a) cF = 0,00292 ; (b) FS = 211 N ;
(c) xcrit = 0,144 m ; (d) Anstieg um 9%)
3. Wasser (15°C) fließt mit einer Geschwindigkeit von 6,00 m/s über eine glatte Platte. Die Platte
ist parallel zur Strömung orientiert. An einer bestimmten Stelle stromab von der Vorderkante der
Platte, ist die Schubspannung an der Platte 42,0 N/m2 und die Grenzschichtdicke ist 2,00 · 10−2 m.
Berechnen Sie die Geschwindigkeit des Wassers in einem Abstand von 2,00 · 10−3 m von der Platte
bedingt durch
a) die logarithmische Geschwindigkeitsverteilung.
b) das Potenzgesetz.
(Lösung: u = 4,21 m/s)
3