Mathematik – Treiber wirtschaftlichen Fortschritts
Werbung

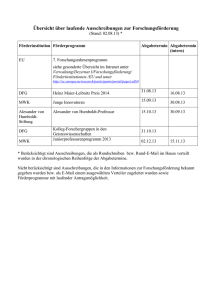
Mathematik – Treiber wirtschaftlichen Fortschritts Beispiele von Projekten durchgeführt im MATHEON, ZIB und in den Berliner Universitäten Prof. Dr. Martin Grötschel MATHEON, ZIB und TU Berlin 20.12.2012, Übersichtsvorlesung in ADM I, WS 2012/13 DFG Research Center MATHEON Mathematics for key technologies 20. 12. 2012 Inhalt 1. Einführung 2. Mathematische Modellierung elektromagnetischer Wellen und deren Folgen 3. Mathematische Modellierung von Strömungen und deren Folgen DFG Research Center Matheon 2 Inhalt 1. Einführung 2. Mathematische Modellierung elektromagnetischer Wellen und deren Folgen 3. Mathematische Modellierung von Strömungen und deren Folgen DFG Research Center Matheon 3 Woher kommt der Name MATHEON ? Vollständige Bezeichnung: DFG-Forschungszentrum Mathematik für Schlüsseltechnologien: Modellierung, Simulation und Optimierung realer Prozesse. 4 MATHEON und seine Trägerinstitutionen Freie Universität Berlin (FU) Humboldt-Universität zu Berlin (HU) Technische Universität Berlin (TU) Weierstraß Institut für Angewandte Analysis und Stochastik (WIAS) Zuse-Institut Berlin (ZIB) DFG Research Center MATHEON 5 Was macht MATHEON ? 6 The problem solving cycle in modern applied mathematics The Real Problem Hard- Software ware Data GUI Implementation in Practice Numerical Solution Simulation Modelling Quick Check: Heuristics Simulation The Application Driven Approach Practitioner Specialist Education Mathematical Model Optimization Algorithmic Implementation Computer Science Design of Good Solution Algorithms Mathematical Theory Pure Mathematics Inhalt 1. Einführung 2. Mathematische Modellierung elektromagnetischer Wellen und deren Folgen 3. Mathematische Modellierung von Strömungen und deren Folgen 4. Weitere Anwendungen DFG Research Center Matheon 8 Die Maxwellgleichungen Die Maxwellgleichungen zur Modellierung elektromagnetischer Wellen (von Langwellen bis Röntgenstrahlen) Skizze der Wellenausbreitung von Heinrich Hertz Annalen der Physik und Chemie N. F. Bd. XXXVI, 1889 James Clerk Maxwell (1831-1879) Maxwellsche Gleichungen 1873 rot H j D t Ampèresches Gesetz rot E B t Faradaysches Gesetz div B 0 div D Fließende Ladungen erzeugen das magnetische Feld Ein veränderliches Magnetfeld erzeugt ein elektrisches Feld Das Magnetfeld hat keine Quellen Die Quellen des elektrischen Feldes sind elektrische Ladungen +Materialgleichungen Funktechnologien Radio Fernsehen Sprechfunk RFID Technische Idee Grundsätzliches Verständnis Geschäftsidee Umsetzung Konkurrenz Verbesserung Mobilfunk Autoschlüssel Funküberwachung Funksteuerung … DFG Research Center Matheon Zusammenarbeit von: Ingenieuren Kaufleuten Juristen Informatikern Mathematikern … 11 Konfiguration von Antennen Isotropic Prediction Available for each potential antenna location Antenna Prediction path loss © Digital Building Model Berlin (2002), E-Plus Mobilfunk GmbH & Co. KG Antenna Configuration Azimuth Tilt Height Antenna Diagram Signal propagation in different directions Martin Grötschel © Digital Building Model Berlin (2002), E-Plus Mobilfunk GmbH & Co. KG, Germany height: 41m, electrical tilt: 0-8°, azimuth 0-120° 12 Interferenz & Abdeckung in einem Berliner Netz Martin Grötschel Wenig Interferenz Gute Abdeckung Viel Interferenz Schlechte Abdeckung 13 Netzoptimierung in Berlin: Last verteilen Überlastete Zellen Martin Grötschel Last umverteilen Weniger Probleme 14 Optimierung: Reduktion der Netwerklast StartKonfiguration Optimierte Konfiguration 20 TX power [W] 0 Adjustment: Azimuth Direction Reduktion Antennen & Interferenz co- & adjacent channel interference cell antenna x x x x site x x x x cell backbone network Martin Grötschel 16 Minimum Interference Frequency Assignment Problem (FAP) FAP ist ein ganzzahliges Optimierungsproblem: min co co cvw zvw vwE co s.t. x f Fv vf vwE ad 1 xvf xwg 1 co xvf xwf 1 zvw ad xvf xwg 1 zvw co ad , zvw 0,1 xvf , zvw Martin Grötschel ad ad cvw zvw v V vw E d , f g d (vw) vw E co , f Fv Fw vw E ad , f g 1 17 Region Berlin - Dresden 2877 Antennen 50 Kanäle InterferenzReduktion: 83.6% Martin Grötschel 18 Spin-Off Firma DFG Research Center Matheon 19 Deutschlandweite GSM 900-Optimierung Optimierung je Region aller Standorte Sektoren Bänder Zusammenführung der Ergebnisse aller Regionen Optimierung eines Streifens entlang der Regionsgrenzen Optimierung des 1800 MHz-Anteils von DualbandSektoren neueste Untersuchung von atesio Martin Grötschel 20 Herausforderungen bei nationalem Netzausbau Abdeckung geht verloren Änderungen an Standorten verschieben Zellflächen Bevölkerungsverteilung (Umsatz) 25% 50% Urban Abschaltung des Roamings reißt Lücken auch in Städten 25% 100% Suburban GSM1800 liefert schwache DeepIndoor-Versorgung Rural Dualband GSM1800 Zu wenige 900er-Kanäle für volle Kapazitätsversorgung 60% Coverage Kapazitätsbedarf wächst Verkehrswachstum erfordert Anpassungen im Access-Netz Regions keine neuen Antennenstandorte, nur Umrüstung bestehender 21 R4 R3 R2 R1 R4 R3 R2 R1 R4 R3 R2 R1 Abdeckung effektiv gewinnen Netz bisher besonders dünn in umsatzschwachen Gebieten Verzahnung von Zellflächen über Bänder hinweg Standort & Topologie-Planung für das DFN-Netz: optimale Lösung KIE Faser KPN GRE ROS DES Faser GL HAM Faser GC BRE Faser vorhanden TUB POT HAN Wellenlänge BIE MUE DUI BRA MAG HUB ZIB GOE KAS LEI FZJ AAC DRE MAR BIR JEN GIE FRA CHE ILM BAY GSI ESF KAI HEI ADH ERL REG FZK STU GAR FTTx-Planung DFG Research Center Matheon 23 FTTx-Planung DFG Research Center Matheon 24 FTTx-Konsortium DFG Research Center Matheon 25 FTTH-Planungsbeispiel DFG Research Center Matheon 26 Inhalt 1. Einführung 2. Mathematische Modellierung elektromagnetischer Wellen und deren Folgen 3. Mathematische Modellierung von Strömungen und deren Folgen 4. Weitere Anwendungen DFG Research Center Matheon 27 Navier-Stokes-Gleichungen Navier-Stokes-Gleichung(en) Die Grundgleichung der Strömungsmechanik Ein System nichtlinearer partieller Differentialgleichungen 2. Ordnung. Du p ' u f ' Dt inkompressibler Fall Navier-Stokes-Gleichungen Allgemeiner: Die kompressiblen Navier-StokesGleichungen Navier-Stokes-Gleichungen Allgemeiner: Die kompressiblen Navier-Stokes- Gleichungen Die Visualisierung der Lösungen ist ein eigenes sehr schwieriges Thema der Mathematik. Der Airbus 380 fliegt beim ersten Start und niemand wundert sich darüber. Ein 1-Million $ Problem des Clay Institutes Flugzeuge Als der A 380 erstmals auf die Rollbahn fuhr und flog, hat sich niemand gewundert. DFG Research Center Matheon 32 Verkehrsprobleme Flugzeuge: sicher, energieminimal, Flugverkehr: kollisionsfreier kostenminimaler Verkehr Flugplan Revenue Management Air Line Crew Scheduling (Piloten, Stewardessen) Robust Tail Assignment (Puffer zum Auffangen von Verzögerungen) Ähnliche Probleme bei Bussen Bahnen DFG Research Center Matheon 33 Mathematik & Flugverkehr Kennt noch jemand Pan Am oder TWA? Warum sind diese Fluggesellschaften verschwunden? Monopole/staatliche Eingriffe & Wettbewerb DFG Research Center Matheon 34 Open Sky & PeopleExpress PEOPLExpress wurde am 30. April 1981 als eine der ersten Billigfluggesellschaften der USA gegründet und nahm im selben Jahr den Flugbetrieb auf. Nach einem phänomenalen Wachstum scheiterte PEOPLExpress schließlich an der Übernahme der ehemaligen Frontier Airlines (nicht zu verwechseln mit der noch heute aktiven, "neuen" Frontier). Obwohl die fusionierte Gesellschaft zur fünftgrößten Fluglinie der USA wurde, zeigte sich, dass die Geschäftsmodelle der beiden Fluglinien einfach zu unterschiedlich waren, um Synergien zu nutzen und am Markt erfolgreich bestehen zu können. Hinzu kam, dass nun auch andere Fluggesellschaften in das Marktsegment der Billigflieger drängten. PEOPLExpress wurde schließlich am 1. Februar 1987 von Continental Airlines übernommen und vollständig in diese integriert. http://de.wikipedia.org/wiki/People_Express DFG Research Center Matheon 35 Reaktion von American Airlines Einführung von Revenue Management (Yield Management) (Dies ist der Grund dafür, dass heute (beinahe) keine zwei Fluggäste in einem Flugzeug denselben Preis bezahlen.) Im Anschluss daran: massive Durchforstung der Effizienz aller Prozesse Konsequenz: Einsatz von Mathematik auf breiter Front. Einsatzplanung von Personal und Gerät, etc. Weitere Konsequenz: Wer nicht nachzog, verschwand vom Markt. DFG Research Center Matheon 36 Workflow Oriented and Integrated Optimization: How fast business processes can follow IT? Planning Slide of LSB Control Crew Management Process Pairing Generation Crew Assignment Hotel, DH, PickUp, Administration Integrated Optimization of the Ressource Aircraft and Crew Maintenance Planning Tail Assignment Maintenance Control Pairing & Roster Maintenance Integrated Recovery of Aircraft and Crew Flight Dispatch Operations Management Process Planning 29 Sep 2005 Chart 37 Optimization in Overview NetLine/Crew Crew Tracking Control Movement Control Hub Control Zukunft der Bahn: Siemens-Sicht Mathematik, Informatik, Ingenieurwissenschaften, Betriebswirtschaft DFG Research Center Matheon 38 Motivation Schweizer Sonntagszeitung 24.08.2008 European „Bottlenecks“ 40 Long Distance Passenger Transport Given Timetabled trips, possible deadheads Railcars Composition rules Maintenance rules Regularity rules Find Train compositions Railcar rotations Objectives Minimize fleet/costs Maximize regularity Scenarios Standard week Dated problem Optimization Overview (Images courtesy of DB Mobility Logistics AG) 41 Timetabled Trips (ICE1 standard week) Optimization Overview Umlaufoptimierung für die DB Fernverkehr AG 42 Öffentlicher Nahverkehr Optimization in Public Transport 43 Fahrzeugeinsatzplanung im öffentlichen Nahverkehr Große Anwendungsfälle: 100 Millionen Variable Martin Grötschel 44 Fahrzeugeinsatzplanung Martin 45 Nahverkehrsnachfrage in Potsdam: O-D-Matrix 46 MATHEON B15: Linienplan Potsdam Optimierung des Linienplans 2010 in Potsdam 47 Pausenregeln in der Dienstplanung Verordnung (EWG) Nr. 3820/85 des Rates vom 20. Dezember 1985 über die Harmonisierung bestimmter Sozialvorschriften im Straßenverkehr ABSCHNITT V Unterbrechungen und Ruhezeit Artikel 7 (1) Nach einer Lenkzeit von 4 1/2 Stunden ist eine Unterbrechung von mindestens 45 Minuten einzulegen, sofern der Fahrer keine Ruhezeit nimmt. (2) Diese Unterbrechung kann durch Unterbrechungen von jeweils mindestens 15 Minuten ersetzt werden, die in die Lenkzeit oder unmittelbar nach dieser so einzufügen sind, dass Absatz 1 eingehalten wird. (3) Im Falle des nationalen Personenlinienverkehrs können die Mitgliedstaaten abweichend von Absatz 1 die Mindestdauer für die Unterbrechung auf nicht weniger als 30 Minuten nach einer Lenkzeit von höchstens 4 Stunden festsetzen. Diese Ausnahmeregelung darf nur in Fällen gewährt werden, in denen durch Unterbrechungen der Lenkzeit von mehr als 30 Minuten der Stadtverkehr behindert würde und in denen es den Fahrern nicht möglich ist, in der Lenkzeit von 4 1/2 Stunden, die der Unterbrechung von 30 Minuten vorausgeht, eine Unterbrechung von 15 Minuten einzulegen. (4) Der Fahrer darf während dieser Unterbrechungen keine anderen Arbeiten ausführen. Für die Anwendung dieses Artikels gelten die Wartezeit und die Nicht-Lenkzeit, die in einem fahrenden Fahrzeug, auf einer Fähre oder in einem Zug verbracht werden, nicht als andere Arbeiten. (5) Nach diesem Artikel eingelegte Unterbrechungen dürfen nicht als tägliche Ruhezeit betrachtet werden. Ralf Borndörfer 48 Einsparungen: Die BVG in Zahlen DFG Research Center Matheon 49 Mathematik – Treiber wirtschaftlichen Fortschritts Beispiele von Projekten durchgeführt im MATHEON, ZIB und den Berliner Universitäten Vielen Dank für Ihre Aufmerksamkeit Prof. Dr. Martin Grötschel MATHEON, ZIB und TU Berlin Übersichtsvorlesung in ADM I, WS 2012/13 DFG Research Center MATHEON Mathematics for key technologies 28. 9. 2012