MS-Grundlagen-Trennsysteme

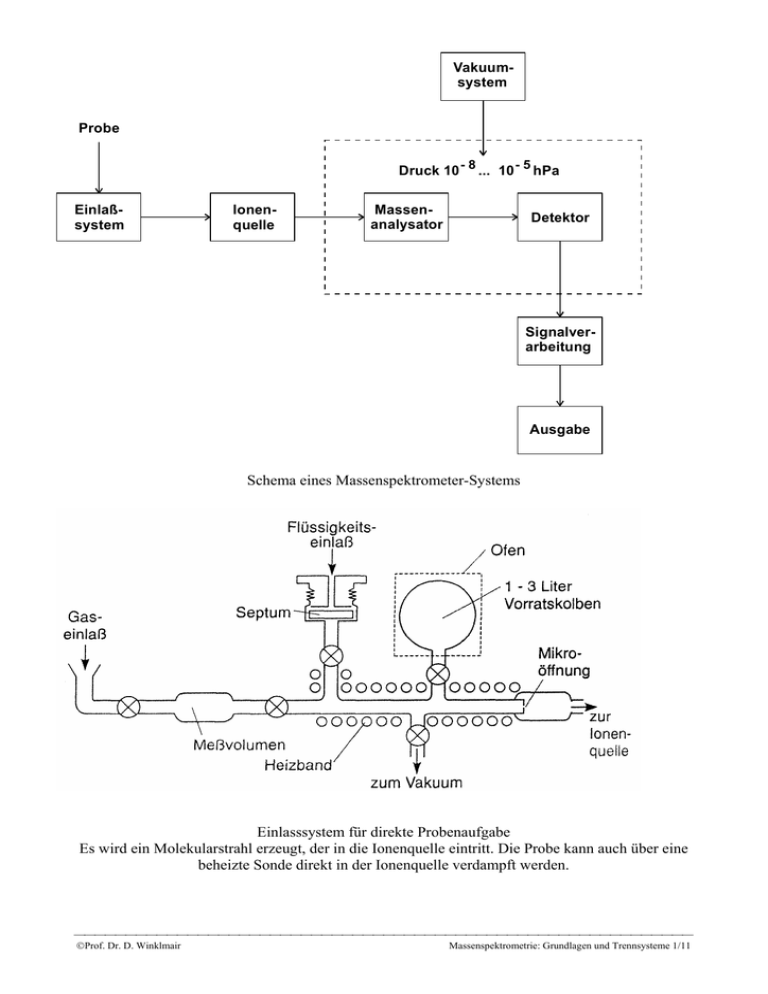
Vakuumsystem
Probe
Druck 10 - 8 ... 10 - 5 hPa
Einlaßsystem
Ionenquelle
Massenanalysator
Detektor
Signalverarbeitung
Ausgabe
Schema eines Massenspektrometer-Systems
Einlasssystem für direkte Probenaufgabe
Es wird ein Molekularstrahl erzeugt, der in die Ionenquelle eintritt. Die Probe kann auch über eine
beheizte Sonde direkt in der Ionenquelle verdampft werden.
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 1/11
Häufigkeit
CH3-CH2-CH2-CH3
10
15
20
25
30
35
40
45
50
55
60
Massenzahl
Massenspektrum von n-Butan (Elektronenstoß-Ionisation mit 70 eV)
Gemessen werden einfach positiv geladene Ionen.
Massenzahl des Molekülions M+: 58
Die übrigen Ionenmassen entstehen folgendermaßen:
Fragmentierungen:
CH3-CH2-CH2-CH3
43
29
15
29
Umlagerungen: CH3-CH2-CH2-CH3 → CH2=CH2 + H2 + CH2=CH2
28
28
CH3-CH2-CH2-CH3 → (CH3-CH2-CH)• + CH4
42
(CH3-CH2-CH2)• → (CH2=CH-CH2)• + H2 → (CH2=C=CH)• + H2
41
39
(CH3-CH2)• → (CH3=C)• + H2
27
CH2=CH2 → CH≡CH + H2
26
Die schwache Linie bei der Massenzahl 44 entsteht durch ein
Radikal-Ion (CH3-CH2-CH2)•+ .
13
C-Atom im
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 2/11
Magnetische Ablenkung
Schema eines einfachen 60°-Sektorfeld-Massenspektrometers mit Elektronenstoßionisation
A: Anode; K: Kathode; D: Düse; E: Beschleunigungselektroden;
P: Vakuumpumpe; Es: Eintrittsspalt; As: Austrittsspalt
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 3/11
Doppelt-fokussierendes Massenspektrometer in Nier-Johnson-Geometrie
Doppelt-fokussierendes Massenspektrometer in Mattauch-Herzog-Geometrie
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 4/11
Elektrische Trennstufe zur Energiefokussierung
K U
In der Realität ist d << R, d.h. E = e
d
Die durchgezogene Linie ist eine zu den Kondensatorplatten konzentrische Bahn positiver Ionen mit der
Energie Wkin.
Aus den Bewegungsgleichungen geladener Teilchen im Zylinderfeld folgt, daß auch Ionen, die unter
K
einem Winkel α von etwas mehr als 90° gegen den Vektor E in das Feld eintreten (gepunktete Bahn),
dann auf den Asutrittsspalt treffen, wenn sie auch die Energie Wkin aufweisen. Für Eintrittswinkel α < 90°
gilt dies nicht.
Für die dargestellte Geometrie, bei der die Brennpunkte der Ionenbahnen im Ein- bzw. Aus-trittsspalt
liegen, ergibt sich γ ≈ 120°37' .
Die gestrichelten Bahnen gelten für Energien W' ≠ Wkin .
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 5/11
Schema eines Quadrupol-Massenspektrometers
Plausibilitätsbetrachtung zur Stabilität von Ionenbahnen im Quadrupolfeld
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 6/11
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 7/11
Geometrie des Quadrupolfeldes
Es ist: ψ = U + V cos ωt
Für das elektrische Potential zwischen den Stäben gilt dann:
ϕ(x, y) =
ψ
(x 2 − y 2)
2
2r
K
K
K
Die Bewegungsgleichungen F = ma = eE = − e grad ϕ lauten:
d 2x
e
+
(U + V cos ωt) x = 0 ;
2
dt
mr2
Mit der Transformation Φ =
a =
d 2y
e
−
(U + V cos ωt) y = 0 ;
2
dt
mr2
d 2z
= 0
dt 2
ωt
und den Abkürzungen
2
4eU
;
mω2r 2
q =
2eV
mω2r 2
ergeben sich die Mathieuschen Differentialgleichungen:
d 2x
d 2y
+
+
Φ
=
− (a + 2q cos 2Φ)y = 0
(
a
2
q
cos
2
)
x
0
und
dΦ 2
dΦ 2
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 8/11
Gebiete stabiler Lösungen der Mathieuschen Differentialgleichungen
Der Massenbereich wird durch gleichzeitige Variation von ΔU und ΔV mit ΔU/ΔV = const. durchlaufen.
Der Stabilitätsbereich zwischen q1 und q2 bleibt dabei konstant.
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 9/11
Schema einer Ionenfalle (Ion Trap)
Die Elektroden haben die Form von Rotationshyperboloiden.
Die Ionisation kann als Elektronenstoß- oder als chemische Ionisation erfolgen.
Schema eines Flugzeit-Massenspektrometers mit Ionenreflektor
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 10/11
Auflösungsvermögen von Magneten und Quadrupolen
Quadrupol:
Bei einer bestimmten Hochfrequenzspannung V wird bei q1 das Ion mit der
2eV
2eV
Masse m 1 =
stabil, während das Ion mit der Masse m 2 =
2 2
q 1ω r
q 2ω2r 2
gerade noch stabil ist. Für die Auflösung gilt also
2eV ⎛ 1
1⎞
⎟ = const.
Δm = m 2 − m 1 = 2 2 ⎜⎜
−
q 1 ⎟⎠
ω r ⎝ q2
Magnet:
Für die Ionenbahn im Magnetfeld gilt: m
v2
v2
= evB und m
= eU b
r
2
Elimination von v und Ausflösen nach m liefert: m =
Daraus folgt:
r 2B 2e
2U b
dm
dr
= 2
;
m
r
dabei ist dr der Bereich der Radien derjeniger Bahnen, die noch in den
Detektor führen; somit ist dr = const.
Also ist:
R =
m
1 r
=
= const.
2 dr
Δm
⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯⎯
©Prof. Dr. D. Winklmair
Massenspektrometrie: Grundlagen und Trennsysteme 11/11