Die Planeten der Sonne: Berechnung der - DJ1YQ - T

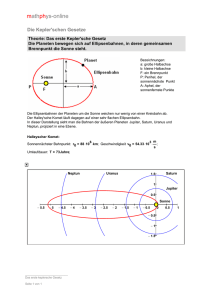
Die Planeten der Sonne: Berechnung der
Umlaufbahnen (A), graphische Darstellung von
Sichtbarkeitszeiten (B).
von Franz J. Bellen, 46537 Dinslaken, E-Mail: [email protected]
A. Berechnung der Umlaufbahnen
A.1. Einführung
Seit Nikolaus Kopernikus (1473 - 1543) ist bekannt, dass
sich die Planeten um die Sonne bewegen und nicht die
Sonne und die Planeten um die Erde. Galileo Galilei
(1564 - 1642), ein Anhänger dieser These, war einer der
letzten bekannten Forscher, der unter Androhung auf
dem Scheiterhaufen verbrannt zu werden, seine „irrigen
Auffassungen“ widerrufen musste. Johannes Kepler
(1571 – 1630) postulierte, dass alle Planeten sich auf
elliptischen Bahnen um die Sonne bewegen, und die
Sonne in einem der beiden Brennpunkte der Ellipse sich
befindet, 1. Keplergesetz. Von den nach ihm benannten
Gesetzen leben wir Satellitenfans noch heute, da seine
Gesetze auch auf Satelliten anwendbar sind.
Man kann einen Planeten als Satellit der Sonne
betrachten und als Programmierübung einmal Elevation
und Azimut als Funktion über die Zeit berechnen. Jupiter
wurde ausgewählt, weil er neben dem Mond einer der
hellsten Himmelskörper ist, den man auch in der
Dämmerung sieht. Mit diesem Planet lässt sich die
eigene Berechnung gut überprüfen (Beam auf die
errechneten Werte stellen). Der Rechengang ist zwar
aufwendig, aber wir haben ja noch genügend Zeit, bis
P3-E gestartet wird. Der Weg bis zum Ziel, die
Antennenpositionen, wird hier grob aufgezeigt. Eine
empfehlenswerte Arbeitsunterlage ist [1], die für die
Berechnungen benutzt wurde.
Ausgang für die Berechnungen sind die Bahndaten
(Keplerelemente) der Planeten Erde und Jupiter. Aus
diesen Daten werden im heliozentrischen-ekliptikalen
Koordinatensystem die ekliptikale Breite b und ekliptikale Länge l berechnet.
A.2.1 Das heliozentrisch-ekliptikale Koordinatensystem
Das Bild Abb.1.5, entnommen aus [1], zeigt eine anschauliche Darstellung des Systems. Koordinatenursprung ist die Sonne, Bezugsebene für die ekliptikale
Breite b ist die Ekliptik und für die ekliptikale Länge l der
Frühlingspunkt (x-Achse). Die z-Achse zeigt zum ekliptischen Nordpol. r ist der Abstand zum Planeten vom
Mittelpunkt der Sonne, oft in Astronomische Einheiten
(AE) angegeben (1 AE = 149597870 km = mittlere
Entfernung Erde-Sonne).
Um ein Vorstellungsvermögen über Betrag und
Änderungen der berechneten Parameter zu bekommen,
wurden Graphiken für einen Zeitraum von 1 Monat
(Januar, 2012) erstellt. Wegen der oft sehr kleinen
zeitlichen Änderungen erfolgt die Darstellung in den
erforderlichen Fällen mit extrem hoher Auflösung.
Beobachtungsort ist Dinslaken, JO31JN.
A.2. Der Rechengang mit Ergebnissen
Folgende Planeten umrunden die Sonne: Merkur, Venus,
Erde, Mars, Jupiter, Saturn, Uranus, Neptun und Pluto.
Die letzten drei sind mit bloßem Auge nicht zu sehen.
Bild 1: Heliozentrische Breite b und Länge l der Erde
Seite 1 von 7
Im ersten Schritt müssen für beide Planeten, Erde und
Jupiter, die Koordinaten b und l berechnet werden. Die
Ergebnisse der Positionen aus Sonnensicht für Januar
2012 zeigen die Bilder 1 und 2.
Aus der Bezeichnung ekliptikale Breite geht schon
hervor, dass dieser Wert für die Erde null sein muss, Bild
1. Die Differenz der l-Werte entspricht unter
Berücksichtigung der Exzentrizität der Erdumlaufbahn
von 0.0167 der Winkeländerung in der gewählten
Zeitspanne, 2. Keplergesetz. Die kleinen Änderungen von
l für den Jupiter, Bild 2, sind auf seine große Entfernung
von 5.2 AE von der Sonne zurückzuführen, 2.
Keplergesetz. Seine Inklination beträgt 1.3 Grad von der
Ekliptik. Das hat ein kleines delta-b zur Folge.
großen Entfernung zum Jupiter und für β an der geringen
Neigung des Jupiters zur Ekliptik.
Bild 3: Geozentrische-ekliptikale Breite β und Länge λ
des Jupiters
Bild 3 zeigt die Parameter ekliptikale Breite β und
ekliptikale Länge λ für den Jupiter. Die Änderungen
beider Größen sind sehr gering im Verlauf von 31 Tagen.
Dieses liegt für λ, wie oben schon erwähnt, an der
großen Entfernung zum Jupiter und für β an der geringen
Neigung des Jupiters zur Ekliptik.
A.2.3 Das geozentrisch-äquatoriale Koordinatensystem
Bild 2: Heliozentrische Breite b und Länge l des Jupiters
A.2.2 Das geozentrische-ekliptikale Koordinatensystem
Im zweiten Schritt wird Jupiter von der Erde aus gesucht.
Dazu dient das geozentrische-ekliptikale Koordinatensystem, Bild Abb. 1.6 aus [1].
Unsere Erde vollzieht eine doppelte Bewegung: Sie dreht
sich in 1 Jahr um die Sonne und in 1 Tag um ihre eigene
Achse. Diese zeigt aber nicht, wie die z-Achsen aus den
vorherigen Systemen auf den ekliptikalen Nordpol,
sondern sie ist um 23.4 Grad geneigt. Um nun die
Koordinaten zum Jupiter zu berechnen, muss ein neues
Koordinatensystem
herangezogen
werden:
das
geozentrische-äquatoriale Koordinatensystem, Bild Abb.
1.7 aus [1].
Der Unterschied zum vorherigen System ist nur der
Koordinatenursprung. Hier ist es der Erdmittelpunkt. Die
Koordinaten haben neue Buchstaben: ∆ ist der Abstand
Erde – Planet, β ist die ekliptikale Breite und λ die
ekliptikale Länge.
Bild 3 zeigt die Parameter ekliptikale Breite β und
ekliptikale Länge λ für den Jupiter. Die Änderungen
beider Größen sind sehr gering im Verlauf von 31 Tagen.
Dieses liegt für λ, wie oben schon erwähnt, an der
Koordinatenursprung bleibt der Erdmittelpunkt, Bezugsebene ist nun der Erdäquator, die Bezugsrichtung ändert
sich nicht; es bleibt der Frühlingspunkt. ∆ ist weiterhin
der Abstand Erde – Planet, die Deklination δ ist der
Winkel zwischen der Linie Erde-Planet und der Äquatorfläche, die Rektaszension α ist der Winkel zwischen
Frühlingspunkt und der Projektion der Linie Erde-Planet
auf den Äquator. Die z-Achse zeigt in Richtung
Erdnordpol.
Seite 2 von 7
Bild 4 zeigt die Deklination δ und die Rektaszension α für
den Jupiter. Die Änderungen im Laufe eines irdischen
Monats sind, verglichen mit Bild 3, fast gleich, während
man im Vergleich ekliptische Breite und Deklination die
Änderung der Bezugsebene der beiden Systeme um 23.4
Grad deutlich erkennt.
Bild 5 zeigt Azimut und Elevation für den Jupiter für den
Standort Dinslaken, JO31JN. Das Bild hat keine
Ähnlichkeit mehr mit den vorherigen Bildern, die
prinzipiell auch die Richtungen zum Jupiter angeben. Da
hier der Tagesrhythmus eingeht, haben wir täglich einen
Planetenaufgang, eine maximale Elevation und einen
Planetenuntergang. Das Bild 5 zeigt auch die Richtungen
an, wenn der Planet Jupiter vom Standort JO31JN nicht
zu sehen ist. Einen Auszug für den 1. Und 31. Januar
Bild 4: Deklination δ und Rektaszension α im
geozentrischen-äquatorialen Koordinatensystem
A.2.4 Das horizontale Koordinatensystem
Nun leben wir Menschen nicht im Erdmittelpunkt
sondern auf der Erdoberfläche, und jeder lebt an einem
anderen Platz. Die Folge ist, dass jeder den Jupiter unter
einem anderen Winkel sieht. Die Ermittlung dieser
Winkel geschieht mit Hilfe des horizontalen
Koordinatensystems, Bild Abb. 1.9 aus [1]. Dieses
System ist dasjenige, mit dem Satellitenfreunde vertraut
sind. Wir bezeichnen allerdings die Höhe der
Astronomen als Elevation und unser Nullpunkt für den
Azimut ist Norden und nicht Süden. Der
Koordinatenursprung ist der Standort des Beobachters,
die Bezugsebene der Horizont, die Bezugsachse die Linie
Zenit-Beobachtungsort-Erdmittelpunkt-Nadir. Weitere
Parameter in diesem System sind die Ortszeit, die eine
feste Differenz zur Greenwicher Zeit (UTC) besitzt, und
das geographische Koordinatennetz der Erde mit seinen
Längen- und Breitengraden. Die Parameter Deklination
und Rektaszension aus dem geozentrisch-äquatorialen
Koordinatensystem (A.2.3) werden in dieses System umgerechnet.
Bild 5: Elevation und Azimut Januar 2012
zeigt Bild 6. Hier ist deutlich zu entnehmen, unter
welchen Koordinaten und wann Jupiter sichtbar ist. Aus
diesem Bild geht auch hervor, dass die täglichen
Sichtbarkeitszeiten und die maximalen Elevationen sich
ändern (wie ein Satellit).
Bild 6: Elevation und Azimut am 01. und 31.01.
A.3. Quellennachweis
[1] Oliver Montenbruck, „Grundlagen der Ephemeridenrechnung“,
Spektrum Akademischer Verlag Heidelberg 2009
Ein Hinweis für Programmierfans: XDS-Excelsior hat die
Weiterentwicklung der kostenlosen Software XDS
Modula-2 wieder aufgenommen. Die letzte Entwicklung
„XDS 2.6 beta“ kann unter
http://www.excelsior-usa.com/xds.html
downgeloaded werden.
Seite 3 von 7
B. Graphische Darstellung von Sichtbarkeitszeiten
B.1. Einführung
In A. hat der Verfasser einen Weg aufgezeichnet, wie
man die Positionen von Planeten berechnet. Als Beispiel
wurde Jupiter gewählt, weil er mit bloßem Auge und
über längere Zeiten beobachtet werden kann. Die Abhandlung soll eine Anregung zum Programmieren sein.
In B. werden die Sichtbarkeitszeiten der Planeten Venus,
Mars, Jupiter und Saturn für das gesamte Jahr 2012
aufgezeigt. Für alle Planeten wird die Sichtbarkeit für
Oktober 2012 gesondert berechnet und dargestellt.
Dieses erhöht für Oktober die graphische Auflösung. Um
zu jeder Tageszeit die genauen Positionen von Azimut
und Elevation zu erfahren, stellt der Verfasser das
Programm „aktParameter.exe“ auf seiner Homepage:
http://dj1yq.homepage.t-online.de/akt.Parameter zur
Verfügung. Das Programm läuft synchron mit der Rechneruhr. Der ausgelesene Zeitwert wird als UTC betrachtet (MEZ berücksichtigen oder besser: Rechneruhr
umstellen).
Die Entfernungen der Planeten von der Erde sind sehr
unterschiedlich. Sie liegen zwischen 0,3 und 11
Astronomischen Einheiten. Die Abstandsänderungen im
Laufe eines Jahres sind ebenfalls erheblich. Bild 7 gibt
einen Überblick über die Entfernungen. Als Vergleich
dazu dient der Abstand des Mondes von der Erde
(Maßeinheit beachten).
einstrahlung eine Beobachtung der Planeten mit dem
Auge nicht zulässt, wird der Zeitraum Sonnenaufgang bis
Sonnenuntergang ausgeblendet, gelbe Fläche. Ist der
jeweilige Planet auch während der Nachtstunden nicht
sichtbar, so erscheint diese Zeitspanne dunkelgrau. Die
bunten Flächen stellen die jeweilige Elevation des
Planeten farbcodiert dar. Die Zahlenwerte können aus
der Tabelle in der Graphik entnommen werden. Die
Farbcodierung ist nicht für alle Bilder gleich.
Die Graphiken wurden für Dinslaken, geographische
Länge = 6.74 Grad Ost, geographische Breite = 51.58
Grad Nord berechnet (JO31JN).
Von der Erde aus gesehen, zählt die Venus zu den
inneren Planeten. Ihre Umlaufzeit um die Sonne ist
geringer als die der Erde, es kommt zu Überholungen.
Am Nachthimmel ist die höhere Umlaufgeschwindigkeit
gegenüber z.B. Saturn zu beobachten, wenn man ein
Zeitinkrement von einigen Stunden wählt. Bild 8 zeigt die
Sichtbarkeit für 2012. Venus ist in der ersten Jahreshälfte
abends und in der zweiten Jahreshälfte morgens zu
sehen. Die Leuchtkraft ist bei klarem Himmel z.T. sehr
hoch. Die Elevationen können Werte bis zu 40 Grad
erreichen.
Interessieren die Sichtbarkeitszeiten für einen bestimmten Monat, so liefern die Monatsbilder eine bessere
Ablesegenauigkeit, hier Bild 9 für Oktober 2012. Die
Beobachtungszeiten sind nur 3 bis 4 Stunden und die
Elevation erreicht nur kurzzeitig mehr als 30 Grad.
Ein ganz anderes Muster zeigt die Sichtbarkeit des Mars
für 2012, Bild 10. Er ist in der ersten Jahreshälfte morgens und abends zu sehen. In der zweiten Jahreshälfte
macht er sich sehr rar. Das verdeutlicht auch die Sichtbarkeit für den Planeten im Oktober, Bild 11.
Ganzjährig sichtbar mit Elevationen von bis zu 60 Grad
ist Jupiter, Bild 12. Bei wolkenlosem Himmel leuchtet es
sehr hell und ist im Oktober morgens und abends zu
sehen, Bild 13.
Bild 7: Entfernung des Mondes sowie der Planeten
Venus, Mars, Jupiter und Saturn von der Erde
B.2. Die Graphiken
Wenn man die Positionen von Saturn kennt, findet man
ihn sehr schnell, sonst ist Suchen angebracht, Bild 14.
Das ist auf die große Entfernung zur Erde
zurückzuführen. Seine maximale Elevation beträgt ca. 30
Grad. Die Sichtbarkeit ist fast ganzjährig. Der
schlechteste Monat ist der Oktober, Bild 15.
Erläuterungen: Die x-Achse gibt die Uhrzeit in UTC, die yAchse die Tage des Jahres 2012 wieder. Da die Sonnen-
Seite 4 von 7
Bild 8: Sichtbarkeit der Venus im Jahr 2012
Bild 9: Sichtbarkeit der Venus im Oktober 2012
Bild 10: Sichtbarkeit des Mars im Jahr 2012
Seite 5 von 7
Bild 11: Sichtbarkeit des Mars im Oktober 2012
Bild 12: Sichtbarkeit des Jupiters im Jahr 2012
Bild 13: Sichtbarkeit des Jupiters im Oktober 2012
Seite 6 von 7
Bild 14: Sichtbarkeit des Saturns im Jahr 2012
Bild 15: Sichtbarkeit des Saturns im Oktober 2012
A./B. Zusammenfassung
Der Teil A. ist als Programmierübung gedacht. Mit Hilfe
der Unterlage [1] müsste es vielen Fans gelingen, die
Ergebnisse nachzuvollziehen.
ten Venus, Mars (leicht rötliches Aussehen), Jupiter und
Saturn dar. Die rechnerische Auflösung der Graphiken
beträgt 6 Minuten, was auch in etwa der Ablesegenauigkeit der Diagramme entspricht. Der Programmieraufwand bis zur fertigen Graphik ist nicht gerade gering.
Aber das sollte keinen daran hindern, es zu versuchen.
Der Teil B. stellt eine Bildersammlung über die Sichtbarkeitszeiten der mit bloßem Auge beobachtbaren Plane-
Seite 7 von 7