Präsentation - walser-h-m.ch
Werbung

Modul 404: Axiomatik und Unterricht!
Formulierungen
Begriffe
Werkzeuge (Tools)
Was gehört wie in den Unterricht?
Explizite Themen (im Lehrplan)
Implizite Themen (lieber nicht im Lehrplan)
„Konstruieren mit Zirkel und Lineal“ Scheibenwischer
Frage: Welcher Teil der Scheibe wird gewischt?
Jetzt ist alles klar:
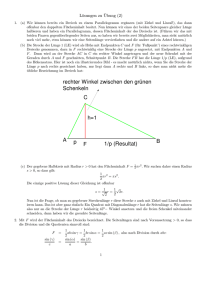
Konstruiere mit Zirkel und Lineal den gesamten Rand desjenigen Gebietes, das vom Scheibenwischer (Strecke [AB]) bei einer Drehung um den Punkt C um 150° im Gegenuhrzeigersinn überstrichen wird. Bemerkung: Der Hebelarm (Strecke [CD]) ist starr mit dem eigentlichen Scheibenwischer (Strecke [AB]) verbunden. B
D
A
C
Jetzt ist alles klar:
Konstruiere mit Zirkel und Lineal den gesamten Rand desjenigen Gebietes, das vom Scheibenwischer (Strecke [AB]) bei einer Drehung um den Punkt C um 150° im Gegenuhrzeigersinn überstrichen wird. Bemerkung: Der Hebelarm (Strecke [CD]) ist starr mit dem eigentlichen Scheibenwischer (Strecke [AB]) verbunden. B
D
A
C
Jetzt ist alles klar:
Konstruiere mit Zirkel und Lineal den gesamten Rand desjenigen Gebietes, das vom Scheibenwischer (Strecke [AB]) bei einer Drehung um den Punkt C um 150° im Gegenuhrzeigersinn überstrichen wird. Bemerkung: Der Hebelarm (Strecke [CD]) ist starr mit dem eigentlichen Scheibenwischer (Strecke [AB]) verbunden. B
D
A
C
Euklid, 365 BC - 300 BC
S'muess eine sy
gar hübsch und fy
Logisches Denken
S'muess eine sy
gar hübsch und fy
p ∧ q
Logisches Denken
p
q
p
q
0
0
0
0
1
0
1
0
0
1
1
1
0 - 1 - Euphorie der 70er Jahre
Lern- und Arbeitstechnik
Euphorie der 90er Jahre
Lern- und Arbeitstechnik
Was einen interessiert, lernt man auch ohne Lerntechnik, und das andere lohnt sich nicht zu lernen.
Euphorie der 90er Jahre
Toolbox of Euclid
Ruler and compass
Zirkel und Lineal
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Elegantere Methode
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
Sportliche Einschränkung: Lineal (ohne Markierungen)
Zirkel mit fester Öffnung
Beispiel: Mittelpunkt einer Strecke
"unlösbare" Probleme
Mit Euklids
Werkzeugen
"unlösbare" Probleme
Mit Euklids
Werkzeugen
• Winkeldrittelung
• Würfelverdoppelung
• Quadratur des Kreises
Winkeldrittelung
Winkeldrittelung
Messen (Transporteur, bei Euklid verboten)
und
Rechnen (Taschenrechner, nicht nur bei Euklid verboten)
Winkeldrittelung
1
4
1 + 1 +! =
+ 16
64
1
4
1− 14
=
1
4
3
4
= 13
Mit Zirkel und Lineal machbar.
Winkeldrittelung
1
4
1 + 1 +! =
+ 16
64
1
4
1− 14
=
1
4
3
4
= 13
Mit Zirkel und Lineal machbar.
Winkeldrittelung
1
4
1 + 1 +! =
+ 16
64
1
4
1− 14
=
1
4
3
4
= 13
Mit Zirkel und Lineal machbar.
Winkeldrittelung
1
4
1 + 1 +! =
+ 16
64
1
4
1− 14
=
1
4
3
4
= 13
Mit Zirkel und Lineal machbar.
Braucht aber unendliche viele Schritte.
Winkeldrittelung
1
4
1 + 1 +! =
+ 16
64
1
4
1− 14
=
1
4
3
4
= 13
Winkeldrittelung
1
4
1 + 1 +! =
+ 16
64
1
4
1− 14
=
1
4
3
4
= 13
Mit Zirkel und Lineal machbar.
Braucht aber unendliche viele Schritte.
Winkeldrittelung
Mechanische Geräte
Winkeldrittelung
Uhr
1
12
Winkeldrittelung
Uhr
Winkeldrittelung
Uhr
Drei-Stunden-Tag
Demo mit Folien
Winkeldrittelung
Einschiebelineal mit zwei Marken (bei Euklid verboten)
A
B
Winkeldrittelung
Einschiebelineal mit zwei Marken (bei Euklid verboten)
a
A
B
Winkeldrittelung
Einschiebelineal mit zwei Marken (bei Euklid verboten)
a
A
B
Winkeldrittelung
Einschiebelineal mit zwei Marken (bei Euklid verboten)
α
3
A
a
B
Warum?
Winkeldrittelung
Einschiebelineal mit zwei Marken (bei Euklid verboten)
α
3
A
a
B
Darum
Winkeldrittelung
Einschiebelineal mit zwei Marken (bei Euklid verboten)
Gerät von Archimedes
Winkeldrittelung
Einschiebelineal mit zwei Marken (bei Euklid verboten)
Gerät von Archimedes
Archimedes von Syrakus, 287 - 212 v. Chr.
Noli tangere circulos meos!
Winkeldrittelung
Noch ein Gerät
Winkeldrittelung
Noch ein Gerät
Winkeldrittelung
Einpassen des Gerätes
Berührung
a
Gerade
durch Scheitel
a
3
Punkt
auf Schenkel
Winkeldrittelung
a
a
3
Winkeldrittelung mit Papierfalten
E
D
F
C
G
a
A
B
Winkeldrittelung mit Papierfalten
E
D
F
D
G
F
G
H
I
C
a
a
A
E
C
B
A
B
Winkeldrittelung mit Papierfalten
E
D
C
Zwei Sachen aufs Mal
F*
F
H*
H
G
A*
I
a
A
B
Winkeldrittelung mit Papierfalten
E
D
C
D
F*
F
G
F
A*
I
H
B
A
α
3
a
A
C
H*
G
F*
H*
H
E
A*
I
B
Winkeldrittelung mit Papierfalten
Beweisfigur
E
D
C
F*
F
H
A
H*
G
A*
I
A'
B
Winkeldrittelung durch Verdreifachung mit DGS
Dynamische Geometrie Software
Demo Winkeldrittelung
Winkeldrittelung durch Verdreifachung mit DGS
zu klein
gerade richtig
zu groß
Würfelverdoppelung
?
Würfelverdoppelung
3
2
Würfelverdoppelung
Evariste Galois
bewies die Unlösbarkeit der Würfelverdoppelung
mit Zirkel und Lineal.
Evariste Galois
1811 – 1832
Quadratur des Kreises
Konstruktion eines Quadrates (mit Zirkel und Lineal),
das den gleichen Flächeninhalt hat wie ein gegebener Kreis. Quadratur des Kreises
Konstruktion eines Quadrates (mit Zirkel und Lineal),
das den gleichen Flächeninhalt hat wie ein gegebener Kreis. Es gibt nur Näherungslösungen. Quadratur des Kreises
Näherungslösung der Ägypter
s = 89 d
Modell und Abstraktion
Modell und Abstraktion
Ein Modell
macht eine Idee
sichtbar
begreifbar
Schon wieder Euklid
Gefordert sein soll:
1. Dass man von jedem Punkt nach jedem Punkt die Strecke ziehen darf,
2. Dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern kann,
3. Dass man mit jedem Mittelpunkt und Abstand den Kreis zeichnen kann,
4. Dass alle rechten Winkel zueinander gleich sind, 5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. Spielregeln
Begriffe
§ Was ist ein "Punkt"?
§ Was ist eine "Gerade"?
§ Was ist ein "Kreis"?
Nicht weiter definierte Begriffe
"Gleichseitiges Dreieck"
§ Drei Punkte
§ Man kann um jeden Punkt einen Kreis durch die beiden anderen Punkte "zeichnen"
Definierter Term (auf der Basis der nicht definierten
Terme "Punkt", "Kreis")
Modelle
2D-Papier
Zahlenpaare (x, y)
Modelle
2D-Papier
Zeichnen
Synthetische Geometrie
Zahlenpaare (x, y)
Rechnen
Analytische Geometrie
Modelle
"Punkt"
2D-Papier
P
Zahlenpaare (x, y)
P(6, 5)
Modelle
"Punkt"
"Gerade"
P ∈g
2D-Papier
P
Zahlenpaare (x, y)
g
P(6, 5)
g
:
y
=
12
x
+
2
Modelle
"Punkt"
"Gerade"
P ∈g
P ∉h
g h
2D-Papier
P
Zahlenpaare (x, y)
g
h
P(6, 5)
g
:
y
=
12
x
+
2
h
:
y
=
12
x
Schon wieder Euklid
Gefordert sein soll:
1. Dass man von jedem Punkt nach jedem Punkt die Strecke ziehen darf,
2. Dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern kann,
3. Dass man mit jedem Mittelpunkt und Abstand den Kreis zeichnen kann,
4. Dass alle rechten Winkel zueinander gleich sind, 5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. Schon wieder Euklid
Gefordert sein soll:
1. Dass man von jedem Punkt nach jedem Punkt die Strecke ziehen darf,
P
Q
P ( 3, 2 ) Q ( 6, 3)
s=
{
}
( x, y ) 3 ≤ x ≤ 6 ∧ y = 13 x + 1
Schon wieder Euklid
Gefordert sein soll:
1. Dass man von jedem Punkt nach jedem Punkt die Strecke ziehen darf,
P
Q
P ( 3, 2 ) Q ( 6, 3)
s=
{
}
( x, y ) 3 ≤ x ≤ 6 ∧ y = 13 x + 1
2. Dass man eine begrenzte gerade Linie zusammenhängend gerade verlängern kann,
P
Q
g=
{
}
( x, y ) x ∈! ∧ y = 13 x + 1
3. Dass man mit jedem Mittelpunkt und Abstand den Kreis zeichnen kann
k
r
M
M ( 3, 2 ) r = 5
k=
{
}
( x, y ) ( x − 3)2 + ( y − 2 )2 = 25
3. Dass man mit jedem Mittelpunkt und Abstand den Kreis zeichnen kann
k
r
M
M ( 3, 2 ) r = 5
k=
{
}
( x, y ) ( x − 3)2 + ( y − 2 )2 = 25
4. Dass alle rechten Winkel zueinander gleich sind,
y = 13 x + 1
y = 4x − 7
y = −3x + 5
y = − 14 x + 3
5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. 5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. 5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. y = 13 x + 1
y = 13 x + 3
P
P ( 3, 4 )
5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. y = 13 x + 1
y = 13 x + 3
P
P ( 3, 4 )
Beispiel einer einfacheren "Geometrie"
Undefinierte Terme: [, ¥, \
Definierte Terme: keine
Axiome:
A1:
Es gibt genau vier [.
A2:
Zwei verschiedene [ sind \ genau ein ¥.
A3:
Jedes ¥ \ genau zwei [.
Modell 1
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = Maus
¥ = Katze
\ = verängstigt durch
/ verängstigt
Modell 1
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = Maus
¥ = Katze
\ = verängstigt durch
/ verängstigt
Es gibt genau sechs Katzen
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Modell 2
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = roter Bindfaden
¥ = blauer Bindfaden
\ = verbunden durch
/ verbindet
Es gibt genau
6 blaue Bindfäden.
Modell 3
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = großer Buchstabe
¥ = Menge von großen Buchstaben
\ = Element von / enthält
Modell 3
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
A, B, C, D
[ = großer Buchstabe
¥ = Menge von großen Buchstaben
\ = Element von / enthält
Modell 3
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
A, B, C, D
{A, B} {A, C} {A, D}
{B, C} {B, D} {C, D}
Satz:
Es gibt genau sechs ¥
[ = großer Buchstabe
¥ = Menge von großen Buchstaben
\ = Element von / enthält
Modell 3
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
A, B, C, D
{A, B} {A, C} {A, D}
{B, C} {B, D} {C, D}
Satz:
Es gibt genau sechs ¥
[ = großer Buchstabe
¥ = Menge von großen Buchstaben
\ = Element von / enthält
⎛ 4⎞
Beweis:
=6
⎝ 2⎠
Modell 4
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = Punkt
¥ = Linie
\ = verbunden durch
/ verbindet
Modell 4
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = Punkt
¥ = Linie
\ = verbunden durch
/ verbindet
Modell 4
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = Punkt
¥ = Linie
\ = verbunden durch
/ verbindet
Tetraeder
Modell 5
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = Linie
¥ = Punkt
\ = inzident in / inzidiert mit Modell 5
A1: Es gibt genau vier [.
A2: Zwei verschiedene [ sind \ genau ein ¥.
A3: Jedes ¥ \ genau zwei [.
[ = Linie
¥ = Punkt
\ = inzident in / inzidiert mit Nominaldefinition
En Chuchitisch,
en Chuchitisch, das isch en Tisch,
wo i de Chuchi isch.
Was ist eine Strecke?
Kürzeste Verbindung
Stau im Zentrum
Stau am Rand
Äquidistante Punkte Stau am Rand
Fin du monde
Äquidistante Punkte 5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. Genau eine Parallele
durch P.
P
5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. P
Genau eine Parallele
durch P.
Existenz
5. Und dass, wenn eine gerade Linie beim Schnitt mit zwei geraden Linien bewirkt, dass innen auf derselben Seite entstehende Winkel zusammen kleiner als zwei Rechte werden, dann die zwei geraden Linien bei Verlängerung ins unendliche sich treffen auf der Seite, auf der die Winkel liegen, die zusammen kleiner als zwei Rechte sind. P
Genau eine Parallele
durch P.
Existenz
Eindeutigkeit
Stau am Rand
P
g
Unendlich viele Parallelen
Kugelgeometrie
Ebene Geometrie (Euklidische Geometrie)
Hyperbolische Geometrie (Nichteuklidische Geometrie)
Euklidische Geometrie: Geometrie in der Ebene
Streifenmodell
Euklidische Geometrie: Geometrie in der Ebene
Euklidische Geometrie: Geometrie in der Ebene
Nichteuklidische Geometrie: Geometrie auf der Kugel
Herleitung aus Sechseckmodell
Nichteuklidische Geometrie: Geometrie auf der Kugel
Nichteuklidische Geometrie: Hyperbolische Geometrie
Herleitung aus Sechseckmodell
Nichteuklidische Geometrie: Hyperbolische Geometrie
Herleitung aus Sechseckmodell