¨Ubungen, Blatt 4

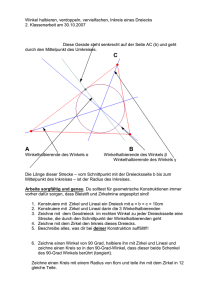
Algebra II
SS 2003
Übungen, Blatt 4
19) Lösen Sie die Aufgabe 21.3.α.
20) Lösen Sie die Aufgaben 21.5.ε und 21.5.ζ.
21) Beim Beweis der Unmöglichkeit der Winkeldreiteilung mit Zirkel und Lineal wird die Irreduzibilität von
X 3 − 3X − 1 gebraucht. Dabei wurde das Kriterium von Eisenstein (nebst einem kleinen Trick) benützt.
Geben Sie gemäss Aufgabe 21.5.ι einen direkten Beweis für die Irreduzibilität.
22) Vor geraumer Zeit wurde unserm Institut der folgende Vorschlag zur Quadratur des Kreises eingereicht
(vgl. die Figur unten):
Man zeichnet das in den Kreis zu verwandelnde Quadrat (z.B. AXY Z) zweimal nebeneinander und
zeichnet um X einen Halbkreis mit Radius AX. Hernach passt man die Strecke P Q (mit P, Q auf dem
Halbkreis) so ein, dass AB = P Q = CD ist. Es wird behauptet, dass AB der Durchmesser des Kreises
mit dem Flächeninhalt des gegebenen Quadrats sei.
a) Zeigen Sie, dass diese Konstruktion den Schönheitsfehler hat, dass sie mit Zirkel und Lineal gar
nicht durchführbar ist. Stellen Sie zu diesem Zweck eine Gleichung für die Strecke x (senkrecht zu
AB) auf.
b) Auch wenn die Konstruktion durchführbar wäre: Welcher Wert kommt für π heraus?
23) Zeigen Sie, dass es unmöglich ist, mit Zirkel und Lineal ein Dreieck aus a, β und der Winkelhalbierenden
wα zu konstruieren.
Tipp: Die Konstruktion geht nicht einmal im Spezialfall, wo β ein rechter Winkel ist (vgl. Figur unten).
In diesem Fall sei W der Schnittpunkt der Winkelhalbierenden mit BC; u sei die Länge von BW . Dann
gilt (warum?)
α
α
u = wα sin und wα sin = (a − u) cos α .
2
2
Setzt man in die zweiten Beziehung den Wert von u ein und drückt cos α durch sin(α/2) aus, so erhält
man eine Gleichung 3. Grades, die sich für die weitere Spezialisierung a = 2wα als irreduzibel erweist.
Machen Sie sich noch klar, dass ein Dreieck mit a = 2, wα = 1 und β = 90◦ auch tatsächlich existiert.
24) Winkeldreiteilung und die Konstruktion von dritten Wurzeln (also z.B. die Verdoppelung des Würfels)
sind möglich, wenn zusätzlich zu Zirkel und Lineal weitere Hilfsmittel zugelassen werden. Ein Beispiel
dazu:
In der Ebene sei die Parabel P mit der Gleichung y = x2 eingezeichnet. Es sei nun erlaubt, Geraden
und Kreise mit P zu schneiden. Zeigen Sie:
√
a) Zu jeder konstruierbaren Zahl r ist auch 3 r konstruierbar. Tipp: Betrachten Sie den Kreis mit
Zentrum ( 2r , 12 ), welcher durch den Nullpunkt geht, und schneiden Sie ihn mit P .
b) Jeder schon konstruierte Winkel ϕ kann dreigeteilt werden. Tipp: Betrachten Sie den Kreis mit
Zentrum ( 18 cos ϕ, 78 ), welcher durch den Nullpunkt geht, und schneiden Sie ihn mit P .
Zu 22)
Z
Zu 23)
B
..
Y
D
..
....................................................
..
..............
.......... .....
... ...........
........ ..
....... ..
.................
.
...
.
.
.
.
.
.
... .................................................................................................................................
........
...........
........
... ......
..... ....
.
.
... .....
.
.
.... ....
... ......
.
.
.
... .....
... ...
.
.
.
...
...
..
..
.
.
...
...
.
.
.
..
...
...
.
.
.
.
...
...
...
...
.
...
.
...
..
..
...
.
.
...
.
...
..
.
.
.
.
...
...
..
.........
.
.
.
...
..
.......
.
..
.
.
.
.
... ....
.
.......
... ...
.... ....
.......
... ...
... ...
... ..
.......
... ....
... ...
.. ..
.......
... ...
... ..
... ....
.......
......
... ...
.......
......
.......
Q
P
x
A
X
C
Schriftlich zu bearbeiten sind die Aufgaben 19), 20), 21), 22).
Abgabe der gelösten Aufgaben (Übungskasten):
Bis Mittwoch, 30. April 2003, 1700 Uhr
C
...
...
...
...
.
.
..
...
...
...
...
.
.
..
...
...
...
...
.
.
..
...
...
...
...
.
.
..
......
...
........
...
........
...
........
........
...
.
.
.
.
.
.
.
.
.
.
.....
...
........
... ..........
... ..........
.........
γ
W
α/2
α/2
A
B