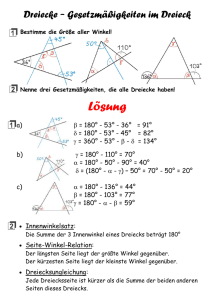
§1 Dreiecke

Mathematische Probleme, SS 2016
Freitag 22.4
$Id: dreieck.tex,v 1.24 2016/04/22 13:58:25 hk Exp $
§1
Dreiecke
1.5
Ähnliche Dreiecke
Wir hatten zwei Dreiecke kongruent genannt wenn in ihnen entsprechende Seiten gleich
lang sind und uns überlegt das dies genau dann der Fall wenn die beiden Dreiecke sich
durch eine Bewegung der Ebene ineinander überführen lassen. Der nun einzuführende Ähnlichkeitsbegriff ist eine Abschwächung des Kongruenzbegriffs. Man nennt zwei
Dreiecke ∆, ∆0 ähnlich zueinander wenn in ihnen entsprechende Winkel gleich sind,
wenn also in den Standardbezeichnungen α = α0 , β = β 0 und γ = γ 0 gelten. Mit den
Kongruenzsätzen des vorigen Abschnitts ist es auch leicht einige Ähnlichkeitskriterien
für Dreiecke anzugeben.
Satz 1.10 (Charakterisierungen ähnlicher Dreiecke)
Seien ∆, ∆0 zwei Dreiecke deren Seiten und Winkel gemäß der Standardbezeichnungen
als a, b, c, α, β, γ beziehungsweise a0 , b0 , c0 , α0 , β 0 , γ 0 benannt sind. Dann sind die folgenden Aussagen äquivalent:
(a) Die Dreieck ∆ und ∆0 sind ähnlich.
(b) Entsprechende Seiten haben dieselben Verhältnisse, also
a
a0 a
a0 b
b0
= 0 , = 0 , = 0.
b
b c
c c
c
(c) Ein Paar entsprechender Winkel und das Verhältniss der angrenzenden Seiten sind
gleich.
(d) Das Verhältniss zweier entsprechender Seiten und die der jeweiligen größeren Seite
gegenüberliegenden Winkel sind gleich.
(e) Zwei Paare entsprechender Winkel sind gleich.
Beweis: (a)⇐⇒(e). Klar da die Winkelsumme im Dreieck immer 180◦ ist.
(a)=⇒(b). Nach dem Sinussatz Satz 8 gilt
a
sin α
sin α0
a0
=
=
=
b
sin β
sin β 0
b0
und die Gleichheit der anderen Verhältnisse ergibt sich analog.
4-1
Mathematische Probleme, SS 2016
Freitag 22.4
(b)=⇒(a). Nach Satz 5 gilt
2
b + c 2 − a2
1 b c a a
α = arccos
= arccos
+ − ·
2bc
2 c b b c
0
c0 a0 a0
1 b
+ − 0 · 0
= α0 ,
= arccos
2 c 0 b0
b c
und analog ergeben sich auch β = β 0 und γ = γ 0 .
(a)=⇒(c). Klar da die Implikation von (a) nach (b) bereits gezeigt ist.
(c)=⇒(b). Sei etwa b/c = b0 /c0 und α = α0 , die anderen beiden Fälle ergeben sich
dann durch Umbezeichnungen. Nach Satz 7 gilt
s
r
0 2
2
a
c
c
c
c0
a0
= 1+
− 2 · cos α = 1 + 0 − 2 0 · cos α0 = 0 ,
b
b
b
b
b
b
und analog folgt auch a/c = a0 /c0 .
(a)=⇒(d). Klar da die Implikation von (a) nach (b) bereits gezeigt ist.
(d)=⇒(c). Beachte das durch das Verhältnis zweier Seiten festgelegt ist welches die
größere der beiden ist, daher entsprechen sich auch die der größeren Seite gegenüberliegenden Winkel in beiden Dreiecken. Bis auf Umbezeichnungen können wir b/c = b0 /c0
und β = β 0 annehmen. Mit Satz 6 folgt
s s 2
2
a
b
b0
a0
2 0
= cos β +
− sin2 β = cos β 0 +
−
sin
β
=
,
c
c
c0
c0
und wir haben die Situation von (c) hergestellt.
Der eben bewiesene Ähnlichkeitssatz hängt eng mit den Strahlensätzen zusammen, und
um dies zu illustrieren wollen wir einmal den Strahlensatz aus dem Ähnlichkeitssatz
herleiten. Diesmal schauen wir uns eine Version des Strahlensatzes über Kreuz“ an,
”
bei dem also der Schnittpunkt des einen Geradenpaars zwischen den beiden parallelen
Geraden liegt.
A
β B’
α
γ
γ
C
β
α
B
4-2
A’
Mathematische Probleme, SS 2016
Freitag 22.4
Gegeben seien also zwei kollineare Tripel ACA0 und BCB 0 bei dem die Geraden AB
und A0 B 0 parallel sind. Nach dem Stufenwinkelsatz haben die beiden Dreiecke ABC
und A0 B 0 C dann gleiche Winkel, sind also ähnlich. Mit dem Ähnlichkeitssatz folgt das
auch entsprechende Seitenverhältnisse in den beiden Dreiecken gleich sind, dass also
|A0 C| |AC|
|A0 C|
|AB|
|A0 B 0 |
|AC|
= 0 ,
= 0 0 und
=
|BC|
|B C| |AB|
|A B |
|BC|
|B 0 C|
gelten, und diese Aussagen sind der Strahlensatz.
Genau wie die Dreieckskongruenz läßt sich auch die Ähnlichkeit von Dreiecken als
die Existenz gewisser Transformationen der Ebene beschreiben. Eine Bewegung der
Ebene war eine Abbildung R2 → R2 die sich aus Verschiebungen, Drehungen und
Geradenspiegelungen zusammensetzen läßt. Etwas formaler kann man die Menge aller
Bewegungen als
AO2 R := {R2 → R2 ; x 7→ Ax + u|u ∈ R2 , A ∈ O2 R}
definieren, wobei O2 R die Menge aller orthogonalen 2 × 2-Matrizen ist, d.h. aller A ∈
R2×2 mit AAt = At A = 1. Es handelt sich dabei auch genau um die Isometrien der
Ebene, dies sind die Abbildungen die den Abstand zwischen Punkten erhalten
AO2 R = {f : R2 → R2 |∀(A, B ∈ R2 ) : |f (A)f (B)| = |AB|},
da dies nur eine Bemerkung ist wollen wir dies hier aber nicht beweisen. Die Menge
AO2 R bildet eine Gruppe und dass zwei Dreiecke kongruent sind bedeutet das sie
sich unter dieser Gruppe aufeinader abbilden lassen. Etwas analoges gilt für ähnliche
Dreiecke man braucht nur eine größere Gruppe. Als zusätzliche Erzeuger benötigen für
die Streckungen. Seien ein Zentrum Z ∈ R2 und ein Streckungsfaktor c 6= 0 gegeben.
Wir lassen hier auch ein negatives c zu, auch wenn dies eigentlich nicht nötig wäre.
Ist A ∈ R2 ein weiterer Punkt, so haben wir den Richtungsvektor A − Z von Z nach
A, diesen skalieren wir mit c, bilden also c · (A − Z), und der Punkt mit diesem
Richtungsvektor ist das Bild von A unter der Streckung %Z,c von Z mit Streckungsfaktor
c, d.h.
%Z,c A := Z + c(A − Z) = (1 − c)Z + cA.
Das Erzeugnis aller Bewegungen und Streckungen ist die Ähnlichkeitengruppe oder
konforme Gruppe des R2
AGO2 R := {R2 → R2 ; x 7→ cAx + u|u ∈ R2 , c ∈ R\{0}, A ∈ O2 R}.
Nun behaupten wir das zwei Dreiecke ∆ = ABC und ∆0 = A0 B 0 C 0 genau dann ähnlich
sind wenn es eine Ähnlichkeitsabbildung f ∈ AGO2 R mit f (A) = A0 , f (B) = B 0 und
f (C) = C 0 gibt. Da Bewegungen und Streckungen Winkel erhalten, ist die Implikation
von rechts nach links dabei klar. Nun nehme umgekehrt an, dass ∆ und ∆0 ähnlich
sind. Sei dann % die Streckung von A mit Streckungsfaktor d := a0 /a, wobei Seiten
4-3
Mathematische Probleme, SS 2016
Freitag 22.4
und Winkel in ∆, ∆0 gemäß der Standardbezeichungen gegeben seien. Das Bilddreieck
∆00 := %(A)%(B)%(C) hat dann nach Satz 10 die Seitenlängen
a00 = a · d = a0 , b00 = b · d =
b 0
b0
· a = 0 · a0 = b0
a
a
und analog c00 = c0 . Damit sind ∆00 und ∆0 kongruent, es gibt also eine Bewegung
γ mit γ(A00 ) = A0 , γ(B 00 ) = B 0 und γ(C 00 ) = C 0 . Folglich ist δ := γ% eine Ähnlichkeitsabbildung mit δ(A) = A0 und δ(B) = B 0 und δ(C) = C 0 . Damit ist Ähnlichkeit
die Äquivalenz von Dreiecken unter der Ähnlichkeitengruppe genau wie Kongruenz die
Äquivalenz von Dreiecken unter der Bewegungsgruppe ist.
1.6
Einige spezielle Punkte im Dreieck
Mit den speziellen Punkten“ in einem Dreieck sind Punkte gemeint die in irgendeiner
”
kanonischen Weise geometrisch aus dem Dreieck heraus konstruiert werden können,
also beispielsweise der Schnittpunkt der Seitenhalbierenden oder der Schnittpunkt der
Mittelsenkrechten. Wir behandeln hier hauptsächlich die vier wichtigsten von diesen,
und dies sind die jeweiligen Schnittpunkte der Seitenhalbierenden, der Winkelhalbierenden, der Mittelsenkrechten und der Höhen. Dies hängen eng mit dem Innkreis und
dem Umkreis eines Dreiecks zusammen. Zur Behandlung dieser Punkte brauchen wir
zum einen den im vorigen Abschnitt eingeführten Ähnlichkeitsbegriff und zum anderen
das sogenannten Mittendreieck eines Dreiecks.
C
B’
A’
Sm
A
C’
B
Gegeben sei ein Dreick ∆ = ABC mit Seiten a, b, c und Winkeln α, β, γ. Dann bilden
wir den Mittelpunkt A0 der Strecke BC, den Mittelpunkt B 0 der Strecke AC und
schließlich den Mittelpunkt C 0 der Strecke AB, es gelten also
a
b
c
|A0 B| = |A0 C| = , |B 0 A| = |B 0 C| = und |C 0 A| = |C 0 B| = .
2
2
2
4-4
Mathematische Probleme, SS 2016
Freitag 22.4
Mit diesen drei Mittelpunkten bilden wir dann das sogenannte Mittendreieck A0 B 0 C 0
und wir wollen einsehen das dieses zu ∆ ähnlich ist und halb so große Seitenlängen
hat.
Lemma 1.11 (Lemma über das Mittendreieck)
Sei ∆ = ABC ein Dreieck mit Mittendreieck ∆0 = A0 B 0 C 0 . Dann sind die vier Dreiecke
∆0 , C 0 BA0 , B 0 A0 C und AC 0 B 0 alle zueinander kongruent und alle ähnlich zu ∆ mit halb
so großen Seitenlängen. Weiter sind A0 B 0 parallel zu AB, A0 C 0 parallel zu AC und B 0 C 0
parallel zu BC.
Beweis: Bezeichne die Seiten und Winkel in ∆ gemäß der Standardbezeichnungen. Im
Dreieck C 0 BA0 ist der Winkel bei B gleich β und das Verhältniss der beiden anliegenden
Seiten ist
1
a
|A0 B|
a
2
=
1 = ,
0
|C B|
c
c
2
also sind ∆ und C 0 BA0 nach Satz 10 ähnlich. Wieder nach Satz 10 ist damit auch
|A0 C 0 |
1
|A0 C 0 |
b
= , also |A0 C 0 | = b,
=
1
0
|BC |
c
2
c
2
das Dreieck C 0 BA0 hat also halb so große Seitenlängen wie ∆. Analog schließen wir für
B 0 A0 C und AC 0 B 0 , und insbesondere sind diese drei Dreiecke zueinander kongruent.
Damit hat das Mittendreieck ∆0 = A0 B 0 C 0 die Seitenlängen
1
1
1
a0 = |B 0 C 0 | = a, b0 = |A0 C 0 | = b und c0 = |A0 B 0 | = c,
2
2
2
ist also ebenfalls zu ∆ ähnlich mit halbierten Seitenlängen und zu den anderen drei
Dreiecken kongruent. Die Aussagen über die Parallelität sind eine unmittelbare Folgerung, da B 0 A0 C ähnlich zu ABC ist stimmen die Winkel dieser Dreiecke bei A0
beziehungsweise B überein, die Gerade BC scheidet A0 B 0 und AB also im selben Winkel und somit sind A0 B 0 und AB parallel. Die beiden anderen Parallelitätsaussagen
ergeben sich analog.
Mit diesem Lemma ist es nun leicht zu sehen, dass die drei Seitenhalbierenden eines
Dreiecks sich in einem Punkt Sm schneiden und dass dieser Punkt weiter die Strecken
AA0 , BB 0 und CC 0 jeweils im Verhältnis 2 : 1 teilt. Tatsächlich ist die letztere Aussage der wesentliche Teil des folgenden Satzes, dass die drei Seitenhalbierenden sich
schneiden folgt aus der Kenntnis dieses Teilungsverhältnisses.
Satz 1.12 (Der Schnittpunkt der Seitenhalbierenden)
Sei ABC ein Dreieck mit Mittendreieck A0 B 0 C 0 . Dann schneiden die drei Seitenhalbierenden AA0 , BB 0 und CC 0 sich in einem Punkt Sm und dieser zerlegt diese Strecken
jeweils im Verhältnis 2 : 1, d.h. es gelten
2|Sm A0 | = |ASm |, 2|Sm B 0 | = |BSm | und 2|Sm C 0 | = |CSm |.
4-5
Mathematische Probleme, SS 2016
Freitag 22.4
Beweis: Wir zeigen zunächst das der Schnittpunkt je zweier der Strecken AA0 , BB 0 ,
CC 0 diese beiden im Verhältniss 2 : 1 teilt. Es reicht dies für die beiden Strecken AA0
und BB 0 zu tun, die anderen beiden Fälle sind dann analog. Sei also S der Schnittpunkt
von AA0 und BB 0 . Nach Lemma 11 sind die beiden Geraden B 0 A0 und AB parallel.
Damit können wir den Strahlensatz auf diese parallelen Geraden und das sich in S
schneidende Geradenpaar AA0 , BB 0 anwenden und erhalten mit Lemma 11
|SA0 |
|SA|
= 1 , also |AS| = 2|SA0 |.
c
c
2
Da dann weiter auch der Schnittpunkt von AA0 und CC 0 die Strecke AA0 im Verhältnis
2 : 1 teilt ist dieser mit S identisch, alle drei Seitenhalbierenden gehen also durch einen
Punkt.
Man nennt den Schnittpunkt Sm der Seitenhalbierenden eines Dreiecks ∆ auch den
Schwerpunkt von ∆. Bevor wir zum nächsten der speziellen Punkte kommen wollen
wir noch auf die Konstruktion des Schwerpunkts mit Zirkel und Lineal eingehen. Diese
können wir offenbar durchführen sobald wir in der Lage sind den Mittelpunkt einer
Strecke zu bestimmen, denn dann können wir die Seitenmittelpunkte A0 , B 0 , C 0 und
somit auch die Seitenhalbierenden AA0 , BB 0 , CC 0 und schließlich ihren Schnittpunkt
finden. Sei also eine Strecke AB gegeben. Mit dem Geodreieck können wir den Mittelpunkt P von AB finden indem erst die Länge |AB| gemessen wird, diese durch Zwei
geteilt wird und schließlich P auf AB mit halbierten Abstand |AB|/2 gezeichnet wird.
Mit einem unmarkierten Lineal müssen wir uns mehr anstrengen, die Konstruktion beruht dann auf der Mittelsenkrechten g der Punkte A, B, also der auf AB senkrechten
Geraden durch P . Nach Aufgabe (1) ist diese auch als die Menge
g = {X ∈ R2 : |AX| = |BX|}
aller Punkte die von A und B denselben Abstand haben gegeben. Die Mittelsenkrechte
können wir mit Zirkel und Lineal finden. Ziehe hierzu Kreise mit Radius |AB| und den
Mittelpunkten A beziehungsweise B. Diese schneiden sich in zwei Punkten C, D, die
beide den Abstand |AB| zu A und B haben, also auf der Mittelsenkrechten von A und
B liegen. Verbinden von C und D liefert damit die Mittelsenkrechte.
4-6
Mathematische Probleme, SS 2016
Freitag 22.4
C
A
g
L
B
M
A
D
Mittelsenkrechte
Lotfußpunkt
Schneiden wir die Mittelsenkrechte CD mit AB so erhalten wir den Mittelpunkt P der
Strecke AB. Außerdem kann diese Konstruktion benutzt werden das Lot von einem
Punkt A auf eine Gerade g zu bestimmen, hierzu bilde einen Kreis mit Mittelpunkt A
der g in zwei Punkten B, C schneidet, dann hat A von B und C denselben Abstand
liegt also auf der Mittelsenkrechten von B und C, d.h. diese ist das gesuchte Lot und
der Schnittpunkt L mit g ist der Lotfußpunkt.
Streng genommen hat diese Konstruktion des Lotfußpunkts noch ein kleines Problem, da der Radius von mit dem Zirkel zu zeichnenden Kreisen als eine bereits vorhandene Strecke gegeben sein muss, müssen wir zunächst eine ausreichend große Strecke
konstruieren können die dann als Radius eines Kreises mit Mittelpunkt A der g in zwei
Punkten schneidet verwendet werden kann. Hierzu überlegt man sich das sich jede
Strecke AB verdoppeln läßt, das sich also AB zu einer Strecke AC doppelter Länge
vergrößern läßt. Durch mehrfache Verdoppelung können dann beliebig große Strecken
konstruiert werden. Dies ist die aus dem ersten Semester bekannte Archimedische Ei”
genschaft der reellen Zahlen“ in ihrer ursprünglichen Bedeutung, Archimedes hat diese
verwendet sie aber Eudoxus zugeschrieben. Zur Verdoppelung von AB ziehe einen Kreis
k mit Radius |AB| um B und verlängere AB bis zu einem von A verschiedenen Schnittpunkt C mit k. Da C auf k liegt ist dann |BC| = |AB|, also |AC| = 2 · |AB| und wir
haben AB zu AC verdoppelt.
4-7