A1-13_Maßeinheiten, Dreiecke, Rechteck, Quadrat

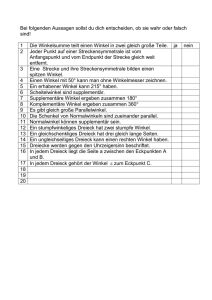
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
ARBEITSBLATT 1-13
Maßeinheiten
1. Längenmaße
1000
km
10
m
10
10
dm
cm
mm
Beispiel: Schreib mehrnamig: 2,032801 km
Lösung: 2,032801 km = 2 km 32 m 8 dm 1 mm
Beispiel: Drücke in km aus: 4 km 20 m 3 cm
Lösung: 4 km 20 m 3 cm = 4,02003 km
2. Flächenmaße
km2
100
100
ha
a
100
100
m2
dm2
3. Volumsmaße
1000
m3
1000
dm3
1000
cm3
mm3
1
100
100
cm2
mm2
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
4. Masse
t
1000
100
10
kg
dag
g
10
dg
10
10
cg
mg
dg......Dezigramm
cg......Zentigramm
mg.....Milligramm
5. Flüssigkeitsvolumen
100
hl
l
10
dl
10
10
cl
ml
Zur Umwandlung dieser Volumsangaben in die üblichen Volumseinheiten gilt
folgender Zusammenhang: 1l = 1 dm3
Der Winkel
Definition: Die Strahlen a und b schließen einen Winkel ein; sie heißen
Schenkel des Winkels. Ihr Schnittpunkt S ist der Scheitel des Winkels. Die Größe
des Winkels können wir also als das Maß für die Drehung auffassen.
2
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
Definition: Als Maß für die Winkelgröße verwenden wir 1°. 1° ist der 90igste Teil
eines rechten Winkels. Der 60igste Teil eines Grades ist eine Winkelminute. 1
Winkelminute hat wiederum 60 Winkelsekunden:
1° = 60´
1´= 60´´
Je nach Winkelgröße unterteilt man die Winkel in verschiedene Arten:
Spitzer Winkel
Stumpfer Winkel
Erhabener Winkel
0° < α < 90°
90°< α <180°
180° < α < 360°
Rechter Winkel
Gestreckter Winkel
α = 90°
α = 180°
Definition: Zwei Winkel, die zusammen 180° ergeben, nennt man
supplementär.
Definition: Zwei Winkel, die zusammen 90° ergeben, nennt man
komplementär.
3
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
Das Dreieck
Bezeichnung:
Merke: Die Beschriftung der Eckpunkte erfolgt entgegen dem Uhrzeigersinn.
Die Seite a liegt immer gegenüber vom Eckpunkt A. Dasselbe gilt
entsprechend für die Seiten b und c.
Besondere Dreiecke
Rechtwinkeliges
Dreieck
Gleichseitiges
Dreieck
Gleichschenkeliges
Dreieck
C
b=a
A
Ein Winkel ist 90° groß.
Die beiden Seiten,
welche den rechten
Winkel bilden heißen
Katheten. Die längste
Seite
heißt
Hypotenuse.
2 Seiten sind gleich
lang. Diese Seiten
bezeichnet man als
Schenkel. Die dritte
Seite bezeichnet man
als Basis.
a
c= a
3 Seiten sind gleich
lang. Alle Winkel sind
60°
Definition: Die Summe aller drei Winkel in einem Dreieck ist stets 180°.
4
B
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
Dreieckskonstruktion
1. Drei Seiten sind gegeben:
Beispiel: a = 36 mm; b = 28 mm; c = 50 mm
Merke: Fertigen Sie zunächst eine Skizze an und tragen sie gegebene Größen
mit Farbstift ein.
Lösung: Wir tragen zunächst die Seite c auf.
A
c
B
Nun nehmen wir die Seite b in den Zirkel, stechen bei A ein und zeichnen
einen Teilkreis
A
c
B
Nun nehmen wir die Seite a in den Zirkel, stechen bei B ein und schlagen ab.
C
a
b
A
c
B
2. 1 Seite und 2 anliegende Winkel:
Beispiel: c = 4 cm; α = 43°; β = 32°
Lösung: Wir tragen zunächst die Seite c auf und konstruieren dann im
Eckpunkt A den Winkel α und im Eckpunkt B den Winkel β. Im Schnittpunkt
der beiden Linien liegt der Eckpunkt C.
5
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
3. 1 Seite, 1 anliegender Winkel und der gegenüberliegende Winkel:
Beispiel: c =5 cm; α= 30°; γ = 70°
Lösung: Da in einem Dreieck die Winkelsumme stets 180° beträgt, läßt sich β
leicht berechnen: β = 180° - 30° - 70° = 80°.
Nun ist die Konstruktion wie im obigen Beispiel.
4. 2 Seiten und eingeschlossener Winkel:
Beispiel: c = 37 mm; b = 29 mm; α = 36°
Lösung: Wir tragen zunächst die Seite c auf. Im Eckpunkt A konstruieren wir
den Winkel α. Der dadurch entstehende Schenkel entspricht der Seite b,
dessen Länge wir abmessen können.
5. 2 Seiten und nicht eingeschlossener Winkel:
Beispiel: c = 54 mm; a = 63 mm; α = 51°
Lösung: Trage die Strecke c auf und errichte im Eckpunkt A den Winkel α.
Dann nehme die Länge der Seite a in den Zirkel, steche in B ein und
schlage auf der Seite b ab.
α
A
c
B
FLÄCHENINHALTE
1. DAS RECHTECK
b
a
A = a ⋅b
6
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
2. DAS RECHTWINKELIGE DREIECK
Es ist leicht ersichtlich, dass einem rechtwinkeligen Dreieck genau die Hälfte
der Fläche eines Rechtecks entspricht:
b
a
A=
a ⋅b
2
3. DAS QUADRAT
Das Quadrat ist ja ebenfalls ein Rechteck, also gilt: A = a ⋅ b
Beim Quadrat sind aber alle Seiten gleich lang, also b = a. Wir erhalten also:
A = a ⋅ a = a2
4. DAS PARALLELOGRAMM
Definition: Die Verbindungslinien zwischen gegenüberliegenden Eckpunkten
nennt man Diagonalen. Bei einem Viereck wird die Verbindungslinie
zwischen den Eckpunkten A und C mit e, jene zwischen B und D mit f
bezeichnet.
Eigenschaften:
Gegenüberliegende Seiten sind gleich lang und parallel.
Gegenüberliegende Winkel sind gleich groß.
Anliegende Winkel sind supplementär.
Die Diagonalen halbieren einander.
Nun überlegen wir uns die Berechnung des Flächeninhaltes:
Wir zeichnen ein beliebiges Parallelogramm und konstruieren im
Punkt D eine Normale (Gerade im rechten Winkel) auf die Seite
a. Eine derartige Linie nennt man die „Höhe auf a“, abgekürzt
ha .
7
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
Wir nehmen nun das Dreieck ADE und fügen es an die Seite BC an:
Das Parallelogramm muss also dieselbe Fläche wie das Rechteck
EFCD haben.
Es folgt also
A = a ⋅ ha
Beispiel: Von einem Parallelogramm kennt man den Flächeninhalt
A = 50 cm2 und die Seitenlänge a = 10 cm. Berechnen Sie ha:
Lösung:
Rechnung
Anmerkungen
Die Formel zur Berechnung der
Fläche
Wir setzen unsere bekannten
Werte ein.
A = a ⋅ ha
50 = 10 ⋅h a
/ : 10
5 = ha
8
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
5. DAS DREIECK
Um den Flächeninhalt eines Dreiecks zu erklären benötigen wir abermals
den Begriff der Höhe:
Definition: Die Höhe ha ist eine Linie im rechten Winkel von der Seite a zum
Eckpunkt A. Die Höhe hb ist eine Linie im rechten Winkel von der Seite b zum
Eckpunkt B. Die Höhe hc ist eine Linie im rechten Winkel von der Seite c zum
Eckpunkt C.
Nun müssen wir uns nur klar werden, dass der Flächeninhalt eines Dreiecks
genau die Hälfte eines Parallelogramms ist:
Folglich berechnet sich die Fläche jedes Dreiecks:
c ⋅ hc
a ⋅ ha
b ⋅ hb
A=
oder A =
oder A =
2
2
2
9
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
6. Die RAUTE (Der RHOMBUS)
Eigenschaften:
Alle vier Seiten sind gleich lang.
Gegenüberliegende Seiten sind parallel.
Gegenüberliegende Winkel sind gleich groß.
Anliegende Winkel sind supplementär.
Die Diagonalen stehen normal aufeinander.
Die Diagonalen halbieren einander.
Die Diagonalen halbieren die Winkel in den Eckpunkten.
Da die Raute nur ein Sonderfall des Parallelogramms ist, gilt auch hier für die
Flächenberechnung: A = a ⋅ ha
Zusätzlich lässt sich für die Raute aber eine zweite Flächenformel herleiten:
Wir erhalten die Fläche der Raute ABCD, indem wir die Dreiecke
ABM und BCM an die Kante AD bzw. CD verschieben. Als
Resultat erhalten wir das Rechteck ACEF, welches denselben
Flächeninhalt wie unsere Raute haben muss. Die Länge dieses
Rechtecks beträgt e, die Breite
A=e⋅
f e⋅f
=
.
2
2
Zusammenfassend noch einmal:
10
f
. Folglich ist die Fläche als
2
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
A = a ⋅ ha oder A =
1. Semester
e⋅ f
2
7. Das DELTOID (DRACHENVIERECK)
Eigenschaften:
Je zwei anliegende Seiten sind gleich lang.
β=δ
Die Diagonalen stehen normal aufeinander.
Die Diagonale e halbiert die Diagonale f.
Die Diagonale e halbiert die Winkel α und γ.
Für die Herleitung der Flächeninhaltsformel gehen wir wie bei der Raute vor:
E
B
A
f
D
M
e
F
C
Wir erhalten die Fläche des Deltoids ABCD, indem wir die
Dreiecke ADM und CDM an die Kante AB bzw. BC
verschieben. Als Resultat erhalten wir das Rechteck AEFC,
welches denselben Flächeninhalt wie unser Deltoid haben
muss. Die Länge dieses Rechtecks beträgt e, die Breite
Folglich ist die Fläche als A = e ⋅
11
f e⋅ f
=
.
2
2
f
.
2
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
1. Semester
8. Das TRAPEZ
Eigenschaften:
Ein Paar gegenüberliegender Seiten ist parallel.
α und δ bzw. β und γ sind supplementär.
Damit wir uns die Flächeninhaltsformel überlegen, duplizieren wir das
Trapez, wenden es und fügen es an das ursprüngliche Trapez an.
Wir haben wieder die Höhe h eingezeichnet. Wir nehmen nun das Dreieck
EFG und geben es an die Seite AD.
Die beiden Trapeze müssen also denselben Flächeninhalt wie das
Rechteck AEGH haben, welches a+c lang und h breit ist. Die Hälfte dieser
Rechtecksfläche muss also der Flächeninhalt des Trapezes sein.
A=
(a + c ) ⋅ h = a + c ⋅ h
2
2
Eine Sonderform des Trapezes ist das gleichschenkelige Trapez:
Zusätzliche Eigenschaften:
Die Seiten b und d sind gleich lang.
12
Mathematik: Mag. Schmid Wolfgang & Lehrer/innenTeam
Die Winkel α und β bzw. γ und δ sind gleich groß.
Die beiden Diagonalen sind gleich lang.
13
1. Semester