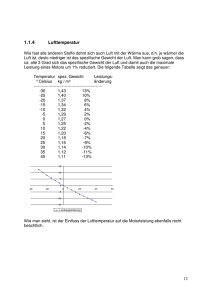
Master-Arbeit Stefan Hunziker

diplomarbeit_stefanhunziker
Auswirkungen des Klimawandels auf die
Gleichgewichts-Oberflächentemperatur von
Seen in globaler Betrachtung
Stefan Hunziker
Masterarbeit, 2010
Auswirkungen des Klimawandels auf die
Gleichgewichts-Oberflächentemperatur von
Seen in globaler Betrachtung
Masterarbeit
ausgeführt an der Eawag,
dem Wasserforschungsinstitut des ETH-Bereichs
Forschungsabteilung Oberflächengewässer
Stefan Hunziker
Lindenhofstrasse 40
8624 Grüt
044 932 26 12
[email protected]
Betreuung durch Dr. Martin Schmid
Eawag, Kastanienbaum
Fakultätsvertretung durch Prof. Dr. Wilfried Häberli
Geographisches Institut der Universität Zürich
April 2010
Zusammenfassung
Das heutige Klima unterliegt starken und rasch fortschreitenden Veränderungen. Diese Effekte sind
mit grösster Wahrscheinlichkeit anthropogen verursacht. Seen reagieren sensitiv auf veränderte
Klimaverhältnisse. Die primäre Reaktion ist die Erhöhung der Oberflächentemperatur. Dies hat
Auswirkungen auf die physikalischen Verhältnisse im See wie auch auf die aquatischen Ökosysteme.
Die Abschätzung zukünftiger Entwicklungen von Seen ist von grosser Bedeutung. Besonders bei
Verwendung von Seewasser zur Trinkwasserversorgung ist die Wasserqualität von grösster
Wichtigkeit. Durch langfristiges Wassermanagement und geeignete Massnahmen können die Folgen
des Klimawandels abgedämpft werden.
Primäres Ziel dieser Arbeit ist eine globale Übersicht der zu erwartenden Veränderungen der
Oberflächentemperatur
von
Gleichgewichtstemperatur
Seen
zur
im
Hilfe
Verlauf
dieses
genommen.
Einer
Jahrhunderts.
Dafür
Wasserfläche
hat
wurde
die
dann
die
Gleichgewichtstemperatur erreicht, wenn der Netto- Energiefluss durch die Wasser- LuftGrenzschicht null ist. Die effektive Oberflächentemperatur eines Sees entwickelt sich stets zur
Gleichgewichtstemperatur hin. Über längere Zeitperioden kann die Oberflächentemperatur gut durch
die Gleichgewichtstemperatur angenähert werden. Die Gleichgewichtstemperatur wird über eine
Energiebilanzgleichung berechnet und ist abhängig von den fünf meteorologischen Faktoren
Lufttemperatur, Dampfdruck, Windgeschwindigkeit, Bewölkung und solare Einstrahlung. Diese
Klimadaten wurden von Simulationen sechs verschiedener Klimamodelle (Atmosphere-Ocean General
Circulation Model, AOGCM) bezogen, welche im Rahmen des 4. Klimaberichtes von 2007 des IPCC
(Intergovernmental Panel on Climate Change) berechnet wurden. Diese Klimadaten liegen in einer
räumlichen Auflösung von 1.1°-4.0° Breite und 1.1°-5.0° Länge sowie einer zeitlichen Auflösung von
Monaten vor. Die benötigten Daten wurden über die klimarelevanten Perioden von 30 Jahren für
1961-1990 und 2070-2099 gemittelt. Die Klimadaten für das zukünftige Klima beruhen auf dem
Treibhausgas-Emissionsszenario SRES A1B. Die Daten für das Basisklima wurden anhand der
beobachteten Konzentrationen von Treibhausgasen modelliert. Mit den Klimadaten wurde die
Gleichgewichtstemperatur des zukünftigen wie auch des Basisklimas berechnet. Durch Subtraktion
der
beiden
Gleichgewichtstemperaturen
wurden
die
zu
erwartenden
Veränderungen
der
Gleichgewichtstemperatur ermittelt. Diese Gleichgewichtstemperatur-Anomalien wurden nicht für
einen spezifischen See erstellt. Sie sollen stattdessen die Temperaturentwicklung aller potentiellen
Seen aufzeigen. Seen können grundsätzlich überall dort auftreten, wo Landflächen sind. Die globale
Gleichgewichtstemperatur-Anomalie
über
Landoberflächen
beträgt
gemittelt
über
alle
Klimadatensätze der sechs verwendeten AOGCMs 2.39°C bei einer Spannbreite von 1.88-3.68°C. Die
Unterschiede zwischen den Resultaten nehmen mit der Abnahme der untersuchten Skala stark zu.
i
Regionale Werte der Gleichgewichtstemperatur-Anomalie sind mit einer grösseren Unsicherheit
verbunden als globale. Allerdings gibt es beträchtliche räumliche Unterschiede. Die Erhöhung der
Gleichgewichtstemperatur in den Tropen erfolgt äusserst uniform. Auch die jahreszeitliche
Entwicklung der Gleichgewichtstemperatur-Anomalie verläuft in tiefen Breiten konstant. Alle
Klimamodelle liefern in den Tropen ähnliche Resultate. Die Resultate können als robust betrachtet
werden. Mit steigender Breite hingegen nimmt die räumliche und zeitliche Variabilität stark zu und
erreicht zwischen 45° und 75° Breite ihr Maximum. In dieser Region sind die Unsicherheiten sehr
gross, die Verwendung von Klimadaten unterschiedlicher AOGCMs führt zu stark verschiedenen
Resultaten. Allerdings gibt es auch in mittleren Breiten Gebiete, für welche einheitliche
Entwicklungen der Gleichgewichtstemperatur berechnet werden. Insbesondere in Nord-Ost-Amerika
wird eine ausserordentlich starke Erhöhung der Gleichgewichtstemperatur prognostiziert. In dieser
Region wird eine starke Zunahme der Lufttemperatur wie auch des Dampfdrucks erwartet. Die
Abhängigkeit der Gleichgewichtstemperatur von der Lufttemperatur nimmt mit steigender Breite zu.
Generell scheint die Gleichgewichtstemperatur in hohen Breiten sensibler auf Klimatische
Veränderungen zu reagieren als in tiefen Breiten.
Es gibt verschieden Formeln, um die Wärmeflüsse durch die Wasser-Luft-Grenzschicht zu berechnen.
Der Austausch einer einzelnen Wärmeformel verändert die Resultate nicht bedeutend. Der Einfluss
der Klimadaten unterschiedlicher Klimamodelle ist von massiv grösserer Bedeutung. Aufgrund der
starken Streuung der Resultate bei Verwendung von Klimadaten unterschiedlicher AOGCMs sind
Untersuchungen anhand nur eines Klimamodelles wenig aussagekräftig. Es sollten möglichst viele
Modelle berücksichtigt und die Resultate gemittelt werden.
Die Resultate dieser Arbeit sind von der Güte der berücksichtigten Klimamodelle abhängig. Eine
grosse Unsicherheit ist die künftige Entwicklung der Treibhausgasemissionen. Die Resultate dieser
Arbeit sind nicht als Prognose zu verstehen. Stattdessen zeigen sich die wahrscheinlichen Folgen des
Klimawandels auf die Oberflächentemperatur von Seen unter Annahme einer Entwicklung der Welt
nach dem SRES A1B-Szenario.
ii
iii
Inhalt
1 Einleitung ............................................................................................................................................. 1
1.1 Relevanz des Themas .................................................................................................................... 1
1.2 Ziele und Fragestellung ................................................................................................................. 2
1.3 Bisherige Arbeiten......................................................................................................................... 3
1.4 Auswirkungen eines veränderten Klimas auf Seen ....................................................................... 5
1.4.1 Temperatur und Stratifikation ................................................................................................ 5
1.4.2 Ökologie ................................................................................................................................. 6
1.4.3 Rückkoppelungen mit dem Klima.......................................................................................... 7
1.4.4 Räumliche Kohärenzen........................................................................................................... 7
1.4.5 Heutiger Stand und Massnahmen ........................................................................................... 7
2 Material und Methoden ........................................................................................................................ 9
2.1 Das Konzept der Gleichgewichtstemperatur ................................................................................. 9
2.1.1 Energieaustausch an der Wasser-Luft-Grenzschicht .............................................................. 9
2.1.2 Beziehung zwischen Wasser- und Gleichgewichtstemperatur ............................................. 10
2.2 Wärmeflüsse ................................................................................................................................ 13
2.2.1 Vertieftere Ausführungen zu einigen Wärmeflüssen ........................................................... 15
2.2.1.1 Solare Einstrahlung........................................................................................................ 15
2.2.1.2 Langwellige Einstrahlung.............................................................................................. 18
2.2.1.3 Latenter Wärmefluss...................................................................................................... 21
2.3 Klimafaktoren.............................................................................................................................. 23
2.3.1 Lufttemperatur...................................................................................................................... 23
2.3.2 Dampfdruck.......................................................................................................................... 23
2.3.3 Windgeschwindigkeit, Bewölkung und solare Einstrahlung................................................ 24
2.4 Statistik........................................................................................................................................ 25
2.5 Klimamodelle .............................................................................................................................. 27
2.5.1 Emissionsszenarien............................................................................................................... 27
2.5.2 Güte der Klimamodelle ........................................................................................................ 28
2.5.3 Verwendete Klimamodelle- und Faktoren............................................................................ 30
2.6 Arbeitsschritte.............................................................................................................................. 33
3 Resultate ............................................................................................................................................. 36
3.1 Globale Mittelwerte..................................................................................................................... 36
3.2 Räumliche Betrachtung ............................................................................................................... 38
3.3 Zeitliche Betrachtung .................................................................................................................. 43
3.4 Energieflüsse ............................................................................................................................... 46
iv
3.5 Einfluss einzelner Klimafaktoren................................................................................................ 49
3.5.1 Gleichgewichtstemperatur bei einem variablen Klimafaktor............................................... 49
3.5.2 Regressionen der Gleichgewichtstemperatur und der Klimafaktoren.................................. 52
3.6 Einfluss unterschiedlicher Wärmeflussformeln .......................................................................... 55
4 Diskussion .......................................................................................................................................... 58
4.1 Eignung des verwendeten Ansatzes ............................................................................................ 58
4.2 Einfluss der Grössenskalen ......................................................................................................... 58
4.3 Einfluss der Jahreszeit................................................................................................................. 59
4.4 Änderungen der Energieflüsse .................................................................................................... 60
4.5 Robustheit der Resultate.............................................................................................................. 61
4.6 Verhältnis Gleichgewichtstemperatur- Klimafaktor ................................................................... 62
5 Schlussfolgerungen und Ausblick...................................................................................................... 64
6 Quellen ............................................................................................................................................... 66
6.1 Literatur....................................................................................................................................... 66
6.2 Abbildungen................................................................................................................................ 70
Abbildungen
Abb. 1. Energieflüsse durch die Wasser-Luft-Grenzschicht ................................................................... 9
Abb. 2. Darstellung der Beziehung zwischen Gleichgewichts- und Wassertemperatur ....................... 11
Abb. 3. Anteil diffuser Strahlung an gesamter solaren Einstrahlung.................................................... 16
Abb. 4. Albedo am Beispiel der CNRM-Basisklimatologie ................................................................. 18
Abb. 5. Vergleich verschiedener Formeln der atmosphärischen Emissivität........................................ 20
Abb. 6. Vergleich verschiedener Formeln der latenten Wärmeflüsse................................................... 22
Abb. 7. Schritte von der Treibhausgasemission bis zur Reaktion des Klimas ...................................... 29
Abb. 8. Höhenmodell der Klimamodelle INCM und MIROC ............................................................. 31
Abb. 9. Erwärmung unter verschiedenen Klimamodellen .................................................................... 32
Abb. 10. Flussdiagramm der wichtigsten Arbeitsschritte ..................................................................... 33
Abb. 11. Seeanteil der Klimamodell INMCM und MIROC ................................................................. 34
Abb. 12. Flächengewichtungsfaktor als Funktion der Breite................................................................ 35
Abb. 13. Boxplot der Gleichgewichtstemperatur-Anomalien aller Klimamodelle............................... 38
Abb. 14. Jährlich gemittelte Veränderung der Gleichgewichtstmperatur ............................................. 39
Abb. 15. Jährlich gemittelte Gleichgewichtstemperatur-Anomalie entlang der Breite ........................ 40
v
Abb. 16. Boxplot der Gleichgewichtstemperatur-Anomalie innerhalb Breitengrad-Intervallen........... 42
Abb. 17. Anzahl Monate im Jahr mit Gleichgewichtstemperatur > °C................................................. 43
Abb. 18. Zeitliche Entwicklung der Gleichgewichtstemperatur-Anomalie ......................................... 45
Abb. 19. Absolute Energieflüsse in Breitengrad-Intervallen................................................................. 46
Abb. 20. Jährlich gemittelte Energieflussanomalien in Breitengrad-Intervallen................................... 48
Abb. 21. Gleichgewichtstemperatur-Anomalien unter dem Einfluss von nur einem Klimafaktor ....... 51
Abb. 22. Gleichgewichtstemperatur-Differen bei Verwendung von Standard- und Alternativformel.. 56
Abb. 23. Differenz der Gleichgewichtstemperatur-Anomalie bei Verwendung von Standard- und
Alternativformen.................................................................................................................... 57
Abb. 24. Gleichgewichtstemperatur mit Standard- und Alternativformeln entlang der Breite ............. 57
Tabellen
Tab. 1. Wichtigste Daten zu verwendeten Klimamodellen ................................................................... 30
Tab. 2. Jährlich gemittelte Gleichgewichtstemperatur-Anomalien über Land- und Seeflächen ........... 37
Tab. 3. Jährlich gemittelte Gleichgewichtstemperatur-Anomalien in Breitengrad-Intervallen............. 40
Tab. 4. Reaktion der Gleichgewichtstemperatur auf Veränderung von Klimafaktor ............................ 53
Tab. 5. Einfluss einzelner Klimafaktore auf Gleichgewichtstemperatur in Breitengrad-Intervallen .... 53
vi
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
1 Einleitung
1.1 Relevanz des Themas
1 Einleitung
1.1 Relevanz des Themas
Das globale Klima unterliegt ausserordentlich starken und rasch fortschreitenden Veränderungen.
Diese können gemessen und beobachtet werden. Die Ursachen dieses Klimawandels sind mit sehr
grosser Wahrscheinlichkeit anthropogen verursacht. Da sich das Klima in den kommenden
Jahrzehnten weiter verändern wird, sind die dabei ablaufenden Prozesse sowie deren Auswirkungen
Gegenstand diverser aktueller Forschungsfragen. Solche Arbeiten sind von grosser Wichtigkeit zur
qualitativen wie auch quantitativen Abschätzung der Auswirkungen des Klimawandels. Sie dienen
Politikern als Entscheidungsgrundlagen und erlauben die Ergreifung von Massnahmen, um den Folgen
des Klimawandels entgegenzutreten.
Eine solide Grundlage für weiterführende Untersuchungen der Auswirkungen des Klimawandels
stellen die Berichte des IPCC (Intergovernmental Panel on Climate Change) dar. In diese Berichte
fliessen die Arbeiten von Wissenschaftlern der unterschiedlichsten Fachgebiete und Länder mit ein.
Der erste Bericht erschien 1990 und wurde seither rund alle 6 Jahre erneuert. Der aktuellste 4.
Klimabericht wurde 2007 veröffentlicht, der nächste wird im Jahr 2014 erscheinen. Wie diverse
andere Forschungsarbeiten stützt sich diese Masterarbeit auf Daten, welche im Rahmens des aktuellen
Klimaberichtes des IPCC generiert wurden.
Der Klimawandel hat vielschichtige Auswirkungen auf Seen. Gemäss MacKay et al. (2009) müssen
für die Verlinkung von Klimaverhältnissen und aquatischen Ökosystemen die Auswirkungen des
Klimawandels auf die physikalischen Verhältnisse verstanden werden. Als die direkteste Reaktion auf
den Klimawandel werden Temperaturanpassungen in Flüssen und Seen erwartet (Whitehead et al.,
2009). Diese primäre Reaktion wird in dieser Masterarbeit untersucht. Die meisten physikalischen
Eigenschaften von Wasser wie auch die meisten biologischen Prozesse sind Funktionen der
Temperatur (Bogan et al., 2003). Deshalb ist die Wassertemperatur einer der Hauptfaktoren in Studien
zu Auswirkungen des globalen Klimawandels auf Süsswasser-Ökosysteme (Mohseni and Stefan). Die
Wassertemperatur an der Seeoberfläche ist des Weiteren ein wichtiger Parameter für
Mischungsprozesse, die Menge des gelösten Sauerstoffes (Goosef et al., 2005), chemische Prozesse
(Vassilis and Gianniou, 2002; Goosef et al., 2005), die Fischpopulation (Whitehead et al., 2009), die
Wachstumsrate und Mortalität aquatischer Flora und Fauna (Goosef et al., 2005) sowie die Toxizität
von Schadstoffen (Fang und Stefan, 1999). Die Prognostizierung der Auswirkungen des
Klimawandels auf Systeme der Natur ist von zentraler Bedeutung, damit nachhaltige
Managementmethoden eingeführt werden können (Arnott et al., 2003). Die grösste Wichtigkeit kommt
der Wassertemperatur und deren Einfluss auf die Wasserqualität aber dort zu, wo Seewasser zur
1
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
1 Einleitung
1.2 Ziele und Fragestellung
Trinkwasserversorgung genutzt wird. Gemäss Whitehead et al. (2009) ist es an der Zeit, bei der
Planung neuer Wasserversorgungs-, urbaner Drainage- und Aufbereitungssysteme den Klimawandel
zu berücksichtigen und neue operative Abläufe zu prüfen.
Der Klimawandel ist ein globales Phänomen und betrifft somit alle Seen weltweit. In dieser Arbeit
werden meist alle Gebiete untersucht, in welchen potentiell ein See liegen könnte. Dies ist über den
Landmassen der Fall. Die Arbeit untersucht demnach keine spezifischen Seen, sondern soll einer
Abschätzung der globalen und grossregionalen Temperaturentwicklung von Seeoberflächen dienen
und die Identifikation von besonders respektive weniger stark betroffenen Gebieten erlauben. Seen
reagieren individuell auf klimatische Veränderungen (z.B. Bleckner, 2005). Dennoch ist bei direkt
vom Klima abhängigen Faktoren eine relativ uniforme räumliche Entwicklung in Seen zu erwarten.
Gemäss Arnott et al. (2003) werden Seen in einer Region ähnlichen Klimafluktuationen ausgesetzt,
weshalb sich stark vom Klima abhängige limnologische Parameter über die Zeit ähnlich entwickeln.
Arnott et al. (2003) erwähnen speziell die Oberflächenwassertemperatur, welche zur Synchronität über
grosse Regionen neige. Auch Leavitt et al. (2009) erwähnen verschiedene Arbeiten, welche den
Energietransfer über ausgedehnte geographische Flächen als relativ uniform beschreiben. Deshalb sei
die saisonale und annuelle Variabilität in physikalischen, chemischen und biologischen Eigenschaften
von Seen synchron (besonders bei ähnlicher Morphometrie und Wärmekapazität).
Bei den modellierten Gewässern in dieser Masterarbeit handelt es sich um potentielle und idealisierte
Seen. Es werden keine spezifischen und lokalen Faktoren wie Zu- und Abflüsse, Mischungsprozesse,
Abschattungseffekte usw. sowie nur eine stark vereinfachte Topographie verwendet. Es können
demnach nicht ohne weiteres Rückschlüsse auf die Änderung der Oberflächentemperatur spezifischer
Sees gezogen werden. Die Arbeit zeigt in erster Linie die vom Hintergrundklima abhängige Tendenz
der Temperaturentwicklungen auf.
1.2 Ziele und Fragestellung
Die Arbeit soll eine globale Abschätzung der Auswirkungen des Klimawandels auf die
Oberflächentemperaturen von Seen ermöglichen, die Anwendbarkeit des Ansatzes erläutern und die
Resultate nach ihrer Robustheit beurteilen. Regionen und jahreszeitliche Perioden sollen ermittelt
werden, in welchen die Oberflächentemperaturen besonders stark vom Klimawandel betroffen sind.
Der Einfluss der Klimafaktoren auf die Wassertemperatur soll abgeschätzt und die dahinter stehenden
Prozesse und Energieflüsse besprochen werden.
Die Arbeit fokussiert sich auf die Untersuchung der Entwicklung der Oberflächentemperatur. Diese
zieht ihrerseits eine grosse Menge an Folgereaktionen nach sich. Diese Folgereaktionen eines
Gewässers auf Änderungen der Oberflächentemperatur werden in Kapitel 1.4 besprochen, danach aber
2
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
1 Einleitung
1.3 Bisherige Arbeiten
nicht weiter behandelt. Die Arbeit beschränkt sich auf grossskalige Untersuchungen. Kleinskalige
Gegebenheiten oder Klimabestandteile können dabei nicht berücksichtigt werden, auch wenn diese
lokal von grosser Bedeutung sind.
In dieser Arbeit wurde eine grosse Menge an Daten generiert. Diese erlauben vielseitige Analysen der
veränderten Oberflächentemperaturen von Seen und des sich wandelnden Klimas. Es hätten also noch
diverse weitere Aspekte untersucht werden können. Die wichtigsten Forschungsfragen wurden wie
folgt formuliert:
• Wie verändern sich die globalen Mittelwerte der Gleichgewichts-Oberflächentemperaturen von
Seen zwischen den Zeitperioden 1961-1990 und 2070-2099?
• Wie unterscheiden sich die Temperaturanomalien in räumlicher und zeitlicher Betrachtung?
• Auf welche sich verändernden Klimafaktoren reagiert die Oberflächen-Gleichgewichtstemperatur
besonders sensitiv?
• Wie unterscheidet sich der Einfluss der Klimafaktoren räumlich?
• Wie unterscheiden sich die Resultate bei Verwendung von Klimadaten unterschiedlicher
Klimamodelle?
• Wie unterscheiden sich die Resultate, wenn partiell unterschiedliche Formeln der Wärmeflüsse zur
Berechnung der Gleichgewichtstemperatur angewandt werden?
1.3 Bisherige Arbeiten
Die Masterarbeit orientiert sich an dem noch unvollständigen und unpublizierten Paper „Effect of a
changing climate on the lake surface temperature: a global perspective and effects on a sensitive lake“
von Schmid et al. (2009). Darin werden globale Reaktionen von Seen auf ein verändertes Klima
besprochen und mit Hilfe einer Energiebilanzgleichung Veränderungen der Energieflüsse und der
Wassertemperatur untersucht. Es wird dabei von einem Gleichgewichtszustand der Energieflüsse
ausgegangen, welcher sich bei einer bestimmten Oberflächentemperatur des Wasserkörpers
(Gleichgewichtstemperatur) einstellt. Dieser Ansatz wird auch in dieser Masterarbeit angewendet. Im
Vergleich zur Arbeit von Schmid et al. (2009) werden Klimadatensätze mehrerer Klimamodelle sowie
unterschiedliche Formeln der Wärmeflüsse verwendet. Zudem werden diverse zusätzliche Aspekte
untersucht.
Die Abhängigkeit der Seewassertemperatur von Klimafaktoren und Klimawandel wurde in
verschiedenen bisherigen Arbeiten untersucht. Dabei wurde mit unterschiedlichen Ansätzen
gearbeitet. Einige Autoren verwendeten den in dieser Masterarbeit benutzten Ansatz und berechneten
die allein von meteorologischen Parametern abhängige Gleichgewichtstemperatur (z.B. Livingstone
3
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
1 Einleitung
1.3 Bisherige Arbeiten
and Imboden, 1989; Keijman, 1974). Fang and Stefan (1999) koppelten die Gleichgewichtstemperatur
zusätzlich an ein See-Modell (MINLAKE96). Verschiedene Arbeiten untersuchen das Verhältnis
zwischen Gleichgewichts- und Flusstemperatur und einige modellierten damit die Auswirkungen des
Klimawandels (Mohseni and Stefan, 1999; Krajewsi et al., 1982; Goosef et al., 2005; Bogan et al.,
2003). In einigen Studien werden in regionale Seen-Modelle nur wenige lokal relevante Klimafaktoren
integriert (Croley II, 1990; Bleckner et al., 2002; Mortsch and Quinn, 1996; Fang and Stefan, 2009;
Stefan et al., 1998). Verschiedentlich wurde die Oberflächentemperatur von Seen anhand empirischer
Zusammenhänge zwischen Wasser- und Lufttemperatur ermittelt und unter Einbezug des erwarteten
Lufttemperatur-Anstieges die zukünftige Entwicklung der Wassertemperatur berechnet (z.B.
Trumpickas et al., 2009). Bei einigen Arbeiten wurden historische Reaktionen von Seen auf
Lufttemperaturschwankungen benützt, um damit die Reaktion des Sees auf die zukünftigen
Klimaschwankungen zu prognostizieren (Arnott et al., 2003; Verburga and Hecky, 2009).
Der letztgenannte Ansatz, die Oberflächenwassertemperatur nur anhand des Klimaparameters
Lufttemperatur zu bestimmen, wurde verschiedentlich als ungenügend kritisiert (Livingstone and
Imboden, 1989; Edinger et al., 1968; Bogan et al., 2003; Goosef et al., 2005). Gemäss Livingstone und
Imboden (1989) spielt die Lufttemperatur auf die Wassertemperatur des Aegerisees in der Schweiz
eine untergeordnete Rolle. Eine reine Erhöhung der Lufttemperatur bewirkt einerseits durch
konvektiven Wärmefluss eine Erhöhung der Gleichgewichtstemperatur, anderseits wird (unter
Annahme konstanter Luftfeuchtigkeit) der Dampfdruck erniedrigt und somit der evaporative
Wärmefluss vom Wasser in die Luft erhöht (Livingstone and Imboden, 1989). Diese beiden Prozesse
gleichen sich grösstenteils gegenseitig aus (z.B. Edinger et al., 1968). Dem ist anzuführen, dass sich
auch bei konstant bleibender Lufttemperatur andere für die Wassertemperatur relevante Klimafaktoren
verändern können. Selbst wenn bei historischen Klimaschwankungen gute Korrelationen zwischen
Wasser- und Lufttemperatur festgestellt wurden, kann nicht vorausgesetzt werden, dass die
zukünftigen Veränderungen des Klimas dieselben Ausprägungen aufweisen.
Die Resultate der vorhergehend erwähnten Arbeiten sind kaum mit den Resultaten dieser Masterarbeit
vergleichbar. Die Studien, welche die zukünftigen Oberflächentemperaturen von Seen modellieren,
haben meist einen starken lokalen Bezug. Für aquatische Seen-Modelle werden weitere Parameter wie
Ein- und Ausfluss, Grösse und Tiefe des Sees, Trophiegrad usw. benötigt. Dies allerdings
verunmöglicht eine grossskalige Betrachtung und den Vergleich von Grossregionen. Zudem
unterscheiden sich die betrachteten Zeitperioden wie auch die verwendeten TreibhausgasEmissionsszenarien von jenen dieser Masterarbeit. Untersuchungen der zukünftigen Änderungen der
Oberflächentemperatur von Seen in einer globalen Betrachtung wurden bis auf die Arbeit von Schmid
et al. (2009) bisher nicht durchgeführt.
4
Auswirkungen des Klimawandels auf die Gleichgewichts1 Einleitung
Oberflächentemperatur von Seen in globaler Betrachtung 1.4 Auswirkungen eines veränderten Klimas auf Seen
1.4 Auswirkungen eines veränderten Klimas auf Seen
Das Klima hat einen umfassenden Einfluss auf Seen. Verschiedene Forschungsarbeiten zeigen, dass
physikalische, chemische und biologische Eigenschaften von Seen rasch auf Veränderungen des
Klimas reagieren (Adrian et al., 2009). Aufgrund dieser Klima-Sensitivität bilden Seen und einzelne
See-Parameter gemäss verschiedenen Forschern geeignete Indikatoren des Klimawandels. Dazu trägt
auch der Umstand bei, dass Seen ein geographisch verteiltes Netzwerk der tiefsten Punkte in der
Landschaft bilden (Williamson et al., 2009). Messbare Reaktionsvariablen sind nach Adrian et al.
(2009) z.B. die epilimnische Wassertemperatur, der Gehalt an gelöstem organischen Kohlenstoff oder
die Planktonzusammensetzung, wobei besonders die Wassertemperatur schnell und direkt auf ein
verändertes Klima reagiert. Klimavariabilität beeinflusst Seen sowohl durch Änderung der Energiewie auch der Massenzufuhr (Niederschlag, suspendierte Partikel, gelöste Substanzen) (Pham et al.,
2008). Die individuellen Reaktionen eines Sees sind abhängig von dessen Höhenlage und
Morphometrie, dem generellen Klima sowie der Vegetation und Landnutzung (Adrian et al., 2009).
1.4.1 Temperatur und Stratifikation
Die Charakteristik der Wassertemperaturen in einem See ist eine Funktion der See-Geometrie, des
trophischen Zustandes und der Klimaverhältnisse (Fang und Stefan, 1999). Da Wasser bei 4°C die
maximale Dichte erreicht, führt bei Temperaturen von über 4°C ein positiver Wärmefluss an der
Wasseroberfläche zu einer Erhöhung der Stabilität, bei Temperaturen unter 4°C hingegen zu einer
Destabilisierung und zu Konvektion (Schmid et al., 2009). Dies zeigt, dass sich der überwiegend
positive Wärmefluss in Folge des Klimawandels je nach Temperaturregime im See stabilisierend oder
destabilisierend auswirken kann. In tiefen tropischen Seen führt die Erwärmung der Wasseroberfläche
zu einer stärkeren Differenz der Wasserdichte und vermindert damit die vertikale Zirkulation in diesen
bereits meromiktischen (keine vollständige Durchmischung) Seen (Verburga and Hecky, 2009). Die
Rate der Nährstofferneuerung nimmt ab und Sauerstoff dringt weniger in tiefe Schichten ein
(Verburga and Hecky, 2009). Besonders in hohen und mittleren Breiten kann der Klimawandel zu
Änderungen des Mischungsregimes von Seen führen. Gemäss Mortsch und Quinn (1996) könnten
viele dimiktische (zwei vollständige Durchmischungen jährlich) Seen im Gebiet der Great Lakes
monomiktisch (eine vollständige Durchmischung jährlich) werden (Mortsch and Quinn, 1996). Dies
würde die Wahrscheinlichkeit von Sauerstoffmangel in verschiedenen Becken erhöhen und dadurch zu
Veränderungen der Chemie und Biota führen (Mortsch and Quinn, 1996). In der oberflächlichen
epilimnischen Schicht hängt die Mischungsdynamik von Seen währen der geschichteten Periode
neben Erwärmungen und Abkühlungen des Wassers auch stark vom Wind ab (MacIntyre et al., 2009).
5
Auswirkungen des Klimawandels auf die Gleichgewichts1 Einleitung
Oberflächentemperatur von Seen in globaler Betrachtung 1.4 Auswirkungen eines veränderten Klimas auf Seen
1.4.2 Ökologie
Der Klimawandel beeinflusst aquatische Ökosysteme hauptsächlich indirekt über Veränderungen der
physikalischen Verhältnisse im See (MacKay et al., 2009). Die Wassertemperatur resp. die
Temperaturstratifikation ist für aquatische Ökosysteme von zentraler Bedeutung. Sie kontrolliert unter
anderem den gelösten Sauerstoff (Stefan et al., 1998; Vassilis and Gianniou, 2002), den Lebenszyklus
aquatischer Organismen (Whitehead et al., 2009), die Toxizität von Schadstoffen (Stefan et al., 1998)
wie auch die Fischerei (Vassilis and Gianniou, 2002). Die meisten chemischen Reaktionen und
bakteriellen Prozesse laufen bei höheren Temperaturen schneller ab (Whitehead et al., 2009).
Demnach ist die biologische Produktivität von der Wassertemperatur abhängig (Vassilis and Gianniou,
2002). Gemäss Bleckner et al. (2002), welche Untersuchungen an einem See in Schweden
durchführten, ist in einem wärmeren Klima eine Erhöhung des Nährstoff-Kreislaufes und der SeeProduktivität zu erwarten. Ein Anstieg der Wassertemperatur muss aber nicht immer zu einer
gesteigerten biologischen Produktivität führen. In tropischen afrikanischen Seen z.B. führte der
Klimawandel zu einer Zunahmen in der Wassertransparenz, was auf eine Reduktion der Produktivität
aufgrund verminderter vertikaler Durchmischung hinweist (Verburga and Hecky, 2009). Gemäss
Whitehead et al. (2009) sind viele Süsswasserspezies kaltblütig, weshalb sie sehr sensitiv auf
Veränderungen der Wassertemperatur reagieren und nur über eine geringe thermische Toleranz
verfügen. So behindern hohe Wassertemperaturen das Wachstum von Kaltwasserfisch-Spezies oder
gefährden gar deren Überleben (Stefan et al., 1998). Ein wärmeres Klima kann auch zur Invasion
ortsfremder Spezies führen (Bleckner et al., 2002). Cyanobakterien (Blaualgen) sind in vielen
Gewässern ein grosses Problem. Nach verschiedenen Studien ist der Erfolg von Cyanobakterien eher
das Resultat komplexer und synergetischer Umweltfaktoren als von einer einzelnen dominierenden
Variablen (Wagner and Adrian, 2009). Jedoch sind viele dieser Umweltfaktoren durch die Temperatur
direkt oder indirekt beeinflusst, was zu einem positiven Selektionsdruck für Cyanobakterien führt, da
diese ihr optimales Wachstum bei höheren Temperaturen haben als andere Algengruppen (Wagner and
Adrian, 2009). Deshalb ist aufgrund der globalen Erwärmung mit einem Anstieg an
Cyanobakterienblüten in Seen zu rechnen (Wagner and Adrian, 2009). Da Veränderungen in
Ökosystemen oft nicht linear, sondern abrupt und diskontinuierlich erfolgen, können bereits geringe
Anomalien der Wassertemperatur signifikante Folgen auf die Ökosysteme in Seen haben (Mueller et
al., 2009).
6
Auswirkungen des Klimawandels auf die Gleichgewichts1 Einleitung
Oberflächentemperatur von Seen in globaler Betrachtung 1.4 Auswirkungen eines veränderten Klimas auf Seen
1.4.3 Rückkoppelungen mit dem Klima
Seen werden nicht nur vom Klimawandel beeinflusst, sie nehmen über Rückkoppelungseffekte auch
Einfluss auf die Klimaentwicklung. Obwohl Seen nur rund 3% der globalen Landoberfläche bedecken
(Downing et al., 2006), sind sie wahre Hotspots als Karbon-Speicher wie auch als
Treibhausgasproduzenten (Williamson et al., 2009). Seen können Orte intensiver Mineralisation
organischen Kohlenstoffes sein (Tranvik et al., 2009). Neuere Studien zeigen, dass in Seesedimenten
jährlich mehr organischer Kohlenstoff abgelagert wird als in Meeressedimenten (Williamson et al.,
2009). Diese Kohlenstoff-Aufnahme wie auch die Produktion von CO2, Methan und Lachgas durch
Mikroorganismen beeinflussen die Konzentration der atmosphärischen Treibhausgase und somit das
atmosphärische Wärmebudget (Tranvik et al., 2009). Die Prognostizierung der zukünftigen
Entwicklung von Seen als Kohlenstoff-Absorber und Treibhausgas-Produzenten ist demnach für den
weiteren Verlauf des Klimawandels nicht unbedeutend. Gemäss Tranvik et al. (2009) führen
insbesondere in tropischen Seen höhere Temperaturen zu verstärktem bakteriellen Stoffwechsel, was
zur Folge hat, dass ein grösserer Teil des organischen Kohlenstoffes als CO2 respiriert wird. Zudem
können die steigenden Temperaturen den Sauerstoffmangel verstärken und dadurch zu einer höheren
Methanproduktion führen (Tranvik et al., 2009). Deshalb haben Seen gemäss Tranvik et al. (2009)
einen flächenmässig überproportionalen Effekt auf den Klimawandel.
1.4.4 Räumliche Kohärenzen
Gemäss Bleckner et. al. (2007) führen grossskalige Kohärenzen von Klimafaktoren (insbesondere der
Lufttemperatur) zu ähnlichen Kohärenzen in vielen See-internen Variablen. Für die Kohärenz der
Klimafaktoren sind unter anderem grossskalige Klimaphänomene wie die Nordatlantische Oszillation
verantwortlich (Bleckner et. al., 2007). Einzelne Parameter im See wie der PH-Wert variieren generell
kleinräumig (Arnott et al., 2003). Je direkter ein Parameter auf Klimaeinflüsse reagiert, desto stärker
ist
die
räumliche
Uniformität
zu
erwarten.
Eine
sehr
direkte
Reaktion
ist
bei
der
Oberflächentemperatur zu erwarten, während bei Ökosystem-Parametern die individuellen SeeCharakteristiken von grösserer Bedeutung sind.
1.4.5 Heutiger Stand und Massnahmen
Der Folgen des aktuellen Klimawandels zeigen sich bereits heute in Seen. Gemäss Williamson et al.
(2009) weisen auch tropische Seen Erwärmungstrends auf, obwohl besonders polare und alpine
7
Auswirkungen des Klimawandels auf die Gleichgewichts1 Einleitung
Oberflächentemperatur von Seen in globaler Betrachtung 1.4 Auswirkungen eines veränderten Klimas auf Seen
Regionen von dem sich wandelnden Klima betroffen sind. So hat der Klimawandel im 20. Jahrhundert
beispielsweise im tropischen, tiefen Tanganyika-See (Afrika) zu einer Zunahme der DichteStratifikation und Schichtungsstabilität geführt (Verburga and Hecky, 2009). Dieser See weist seit
1913 eine jährliche netto Wärmeabsorption von 0.4 Wm-2 auf (Verburga and Hecky, 2009).
Die Auswirkungen der erwarteten Klimaänderungen auf spezifische Seen werden von verschiedenen
Autoren als schwerwiegend beschrieben. So erwarten Mooij et al. (2005) bei holländischen Seen eine
stärkere Eutrophierung, eine Verringerung verschiedener Vogel-Spezies und eine vermehrte
Ausbreitung von Krankheiten, welche von Stechmücken übertragen werden. Beim schwedischen
Erken-See wird erwartet, dass sich die nährstofflimitierte Phytoplankton-Population zu einer
lichtlimitierten wandelt (Bleckner et al., 2002; MacKay et al., 2009). Aufgrund solcher Resultate
können
wasserwirtschaftliche
Massnahmen
ergriffen
werden,
um
diesen
Entwicklungen
entgegenzuwirken. Mooij et al. (2005) erwähnen als solche Massnahmen die Reduktion des
Nährstoffeintrages in die Seen, die Entwicklung der Uferzone und der Koordination von
Wasserwirtschaft und Fischerei.
8
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.1 Das Konzept der Gleichgewichtstemperatur
2 Material und Methoden
2.1 Das Konzept der Gleichgewichtstemperatur
2.1.1 Energieaustausch an der Wasser-Luft-Grenzschicht
Die gespeicherte Energie in Seen wird durch Energieaustausch an der Wasseroberfläche und zu einem
viel geringeren Ausmass durch Wärmeflüsse an der Wasser-Sediment-Grenzschicht sowie
Energietransfers
durch Ein- und
Ausfluss
gesteuert
(Henderson-Sellers,
1986).
Da
der
Energieaustausch hauptsächlich über die Wasser-Luft-Grenzschicht erfolgt (Henderson-Sellers, 1986;
Edinger et al., 1968), ist das Klima einer der wichtigsten Faktoren für die Temperatur eines
Wasserkörpers (Edinger et al., 1968). Der Wärmeaustausch erfolgt durch kurz- und langwellige
Strahlung, latenten und konvektiven Wärmefluss (Schmid et al., 2009; Edinger et al., 1968;
Henderson-Sellers, 1986). Diese Wärmeflüsse werden in Abb. 1. dargestellt. Auch Niederschlag führt
zu einem Energietransfer an der Wasseroberfläche. Dieser Wärmefluss ist über längere Zeitperioden
(Wochen) verglichen mit den anderen Wärmeflüssen an der Wasser-Luft-Grenzschicht klein (Mohseni
and Stefan, 1999) und kann vernachlässigt werden (Henderson-Sellers, 1986). Wärmeflüsse zwischen
Wasser und Sediment werden bei längeren Zeitperioden (mehr als ein Tag) insignifikant und können
vernachlässigt werden (Bogan et al., 2003; Mohseni and Stefan, 1999).
HS
HA
HW
HV
HC
Abb. 1. Energieflüsse durch die Wasser-Luft-Grenzschicht. Dabei ist HS die in den Wasserkörper eindringende
solare Einstrahlung, HA die langwellige Einstrahlung, HW die langwellige Ausstrahlung, HV der latente
Wärmefluss (Evaporation und Kondensation) und HC der konvektive Wärmefluss. Man beachte, dass der
Energietransport bei den radiativen Wärmeflüssen in eine Richtung, bei den turbulenten Wärmeflüssen hingegen
in beide Richtungen möglich ist.
9
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.1 Das Konzept der Gleichgewichtstemperatur
Der Netto-Wärmefluss (Hnet) wird mit einer Energiebilanzgleichung beschrieben und ist gegeben
durch die Summe der einzelnen Energieflüsse
Hnet = HS + HA + HW + HV + HC
(1)
wobei HS die ins Wasser eindringende solare Einstrahlung ist, HA und HW sind die langwellige Einresp. Ausstrahlung, HV ist der latente Wärmefluss (Evaporation und Kondensation) und HC der
konvektive Wärmefluss. Ein positiver Netto-Wärmefluss bedeutet eine Energieaufnahme des Sees, ein
negativer Netto-Wärmefluss einen Energieverlust des Sees an die Atmosphäre. Die Wärmeflüsse
haben die Einheit Wm-2.
Die Gleichgewichtstemperatur wird nun definiert als die Oberflächentemperatur des Wassers, bei
welcher der Netto-Wärmefluss 0 entspricht (Edinger et al., 1968) und somit die gespeicherte Energie
im Wasserkörper konstant bleibt. Es wird gleich viel Energie aufgenommen und abgegeben, das
System befindet sich in einem Gleichgewicht.
Der Energieaustausch durch die Wasser-Luft Grenzschicht und somit die Gleichgewichtstemperatur ist
von folgenden fünf meteorologischen Parametern abhängig: Bewölkung, Windgeschwindigkeit,
Luftfeuchtigkeit, Lufttemperatur und Globalstrahlung (Edinger et al., 1968; Livingstone and Imboden,
1989). Gemäss Livingstone und Imboden (1989) sind Veränderungen der Gleichgewichtstemperatur
nur von den Klimafaktoren Bewölkung, Windgeschwindigkeit, Luftfeuchtigkeit und Lufttemperatur
abhängig, da die Solarstrahlung als konstant und als Funktion der Bewölkung betrachtet werden kann.
In dieser Arbeit wird die solare Einstrahlung allerdings als Klimaparameter behandelt, da diese neben
der Bewölkung von weiteren Faktoren wie der Aerosolkonzentration beeinflusst wird. Sofern also die
Daten der benötigten meteorologischen Parameter bekannt sind, kann die GleichgewichtsOberflächentemperatur eines potentiellen Sees an jedem beliebigen Ort der Welt berechnet werden.
Die Gleichgewichtstemperatur erlaubt somit eine nicht lokal oder regional gebundene Abschätzung
der zukünftigen Entwicklung der Seewassertemperaturen.
2.1.2 Beziehung zwischen Wasser- und Gleichgewichtstemperatur
Die Differenz zwischen der Gleichgewichtstemperatur eines Wasserkörpers und der effektiven
Wassertemperatur an der Oberfläche ist normalerweise relativ gering für Mittelungen über längere
Zeitperioden (Tage, Wochen oder Monate) (Edinger et al., 1968). Für sehr kurze Zeitperioden ist dies
nicht der Fall. Während eines Tages beispielsweise zeigt die Gleichgewichtstemperatur eine viel
grössere Amplitude auf als die Oberflächentemperatur des Wassers (Edinger et al., 1968). Die
Wassertemperatur entwickelt sich stets zur Gleichgewichtstemperatur hin (Edinger et al., 1968).
10
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.1 Das Konzept der Gleichgewichtstemperatur
Dabei ist die Rate des Wärmeaustausches S gegeben durch
S = K (Teq - Tsurf)
(2)
wobei K der thermische Austauschkoeffizient, Teq die Gleichgewichtstemperatur und Tsurf die
Oberflächenwassertemperatur ist (Edinger et al., 1968; Mohseni and Stefan, 1999). K ist eine Funktion
von Lufttemperatur, Taupunkttemperatur und Windgeschwindigkeit (Mohseni and Stefan, 1999). Wird
K als konstant angenommen, nähert sich die Wassertemperatur der Gleichgewichtstemperatur
exponentiell an (Edinger et al., 1968).
Bei einem periodischen Temperaturverlauf (z.B. Tag, Jahr) wird die maximale Wassertemperatur im
Vergleich zur maximalen Gleichgewichtstemperatur verzögert erreicht (Edinger et al., 1968). Unter
normalen
Bedingungen
kreuzen
stündlich
gemittelte
Wassertemperaturen
die
Gleichgewichtstemperatur zweimal täglich und bei monatlicher Mittelung zweimal jährlich, da
Aufwärmung und Abkühlung abhängig von den täglichen resp. jährlichen Zyklen alternieren (Edinger
et al., 1968). Nimmt man den einfachen Fall einer komplett durchmischten Wassersäule, welche nur
auf Wärmeflüsse an der Oberfläche reagiert, entspricht der Wärmefluss durch die Wasseroberfläche
der zeitlichen Änderung der gespeicherten Energie in der Wassersäule (Edinger et al., 1968). Dieser
idealisierte Fall wird in Abb. 2. dargestellt.
Gleichgewichtstemperatur
W assertemperatur
Temperatur (°C)
dT
0
dt
Monate
12
Abb. 2. Beziehung zwischen Gleichgewichtstemperatur und der Temperatur einer vollständig durchmischten
Wassersäule während eines Jahreszyklus. Gleichgewichts- und Wassertemperatur kreuzen sich zweimal jährlich.
Die Amplitude der Wassertemperatur ist kleiner (dT) und erreicht ihr Maximum und Minimum mit einer
zeitlichen Verschiebung zur Gleichgewichtstemperatur (dt) (nach Edinger et al., 1968).
Bei geringer Tiefe der vollständig durchmischten Wassersäule kommen die Kurven der
Gleichgewichts- und Wassertemperatur bei monatlicher Mittelung praktisch aufeinander zu liegen.
Wird die Wassertiefe erhöht, steigt die Wärmespeicherkapazität der Wassersäule. Die zeitliche
11
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.1 Das Konzept der Gleichgewichtstemperatur
Verschiebung (dt) nimmt zu, wie auch die Differenzen der beiden Maximal- (dT) resp.
Minimaltemperaturen. Die Kurve der Wassertemperatur flacht ab. Derartige Effekte sind insbesondere
bei Seen mit grosser thermischer Speicherkapazität zu erwarten. Dies ist der Fall bei gut
durchmischten, tiefen Seen sowie während der periodischen totalen Durchmischung (plötzlicher
Einbezug
viel
grösserer
Wassermassen).
Das
Verhältnis
zwischen
Wasser-
und
Gleichgewichtstemperatur kann also über die Zeit starken Variationen unterliegen.
Das Wasser in Flüssen kann gut als Ansammlung völlig durchmischter Wassersäulen beschrieben
werden. Deshalb eignet sich die Gleichgewichtstemperatur zur Annäherung der Wassertemperatur von
Flüssen (Mohseni and Stefan, 1999; Krajewski et al., 1982). Bogan et al. (2003) stellten bei
Untersuchungen an Flüssen in den westlichen und zentralen USA einen linearen Zusammenhang
zwischen Gleichgewichts- und Flusstemperatur fest, welcher bei jährlichen gemittelten Werten und
Verwendung kalibrierter Daten der Gleichgewichtstemperatur (Abschattung, Windschatten usw.) eine
Steigung von 1 aufweist. Flüsse sind aufgrund ihrer flächenmässig sehr geringen Ausdehnung viel
stärker von lokalen Faktoren wie der Abschattung von Sonne und Wind durch Vegetation und
Topographie beeinflusst als Seen. Eine Kalibrierung der Gleichgewichtstemperatur für spezifische
Flüsse drängt sich deshalb auf. Die Resultate dieser Arbeit sind demnach nur für Fliessgewässer
relevant, welche über grosse Distanzen kaum von lokalen Faktoren beeinflusst werden.
Im Gegensatz zu Flüssen weisen Seen oft eine thermale Stratifikation auf. In solchen Seen ist die in
dieser Arbeit berechnete Gleichgewichtstemperatur nicht für die gesamte Tiefe sondern nur für die
oberste, gut durchmischte Wasserschicht relevant. Die Gleichgewichtstemperatur ist für die folgenden
Schichten verschiedener Seetypen bestimmend:
• Polymiktische Seen (meist seicht und regelmässig völlig durchmischt): gesamte Wassersäule
• Dimiktische Seen (zwei Perioden stabiler Schichtung im Sommer und Winter, dazwischen
komplette Durchmischung): Epilimnion
• Monomiktische Seen (Durchmischung einmal jährlich): Epilimnion
• Seen ohne vollständige Durchmischung: Epilimnion
Von
diesen
Seetypen
lassen
sich
die
polymiktischen
Seen
am
besten
mit
der
Gleichgewichtstemperatur beschreiben. Hauptsächlich der Wind sorgt für eine regelmässige
Durchmischung. Die meisten Seen der Welt sind klein und seicht (Downing et al., 2006) und
entsprechen damit diesem Seetyp. Beispielsweise sind die Süsswasserseen in Holland überwiegend
seicht mit Tiefen von 1 bis 5 Metern (Mooij et al., 2005). Keijman (1974) konnte bei einer
Untersuchung an einem solchen See in Holland die Wassertemperatur mit Hilfe der
Gleichgewichtstemperatur mit Abweichungen von ein paar wenigen Zehntel-Graden beschreiben.
Seichte Seen haben eine geringere Wärmespeicherkapazität als tiefe Seen und reagieren deshalb
schneller auf ein verändertes Klima. Gemäss Verburga und Hecky (2009) stossen seichte Seen bei
einem sich erwärmenden Klima mehr Energie aus, während sich der Wärmeausstoss von tiefen Seen
12
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
nur langsam erhöht. Bei dimiktischen und monomiktischen Seen wird es während der Auflösung der
Stratifikation zu verstärkten Differenzen zwischen Gleichgewichts- und Oberflächentemperatur
kommen, da sich die Tiefe der durchmischten Wassersäule in kurzer Zeit massiv vergrössert.
2.2 Wärmeflüsse
Es gibt diverse Formeln, mit welchen die Wärmeflüsse an der Wasser- Luft-Grenzschicht berechnet
werden können. Ein Grossteil dieser Formeln basiert auf empirischen Beobachtungen, einige auf
physikalischen Berechnungen. Nicht alle Formeln eignen sich gleichermassen für einen bestimmten
Zweck oder ein bestimmtes Untersuchungsgebiet. Der Auswahl der Formeln der Energieflüsse ist
demnach grosse Beachtung zu schenken. Wie sich unterschiedliche Formeln der Wärmeflüsse auf die
Endresultate auswirken können, wird in Kapitel 3.6 anhand des Einsatzes zweier alternativen Formeln
exemplarisch untersucht. In dieser Arbeit wurden hauptsächlich dieselben Formeln verwendet wie in
der Arbeit von Schmid et al. (2009). Die kurz- und langwellige Einstrahlung (HS resp. HA), die
langwellige Ausstrahlung HW sowie der latente und konvektive Wärmefluss (HV und HV_alt resp. HC)
werden wie folgt berechnet:
H S = H S 0 ⋅ (1 − A)
(3)
∧
H A = (1 − rA ) ⋅ E A ⋅ σ ⋅ T air
4
(4)
 e
E A = 1.24 ⋅ (1 + 0.17 ⋅ C ) ⋅  ∧ A

 T air
2
1/ 7




(5)
E A _ alt = (1 + 0.17 ⋅ C 2 ) ⋅ (1.0 − 0.26 ⋅ exp(−7.77 ⋅ 10 −5 ⋅ Tair ))
2
∧
H W = −0.97 ⋅ σ ⋅ T surf
4
(7)
H V = −(e S − e A ) ⋅ (4.4 + 1.82 ⋅ u10 + 0.26 ⋅ (Tsurf − Tair ))
H V _ alt = −(eS − e A ) ⋅
(6)
11
⋅ (1 + 0.2237 ⋅ u8 ) ⋅ LV
30
(8)
(9)
13
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
 b ⋅ Tair 

eS = a ⋅ exp
 Tair + c 
H C = Bowen ⋅ H V ⋅
2 Material und Methoden
2.2 Wärmeflüsse
(10)
(Tsurf − Tair )
(11)
(e S − e A )
HS0 ist die Solarstrahlung über der Wasseroberfläche, A der Anteil reflektierter kurzwelliger Strahlung
an der Wasseroberfläche, rA der Anteil reflektierter langwelliger Strahlung an der Wasseroberfläche
(=0.03), EA die atmosphärische Emissivität und EA_alt eine alternative Formel für EA, σ die StefanBoltzmann-Konstante (=56.7·10-9Wm-2K-4), Tair und Tsurf sind die Luft resp. Seeoberflächentemperatur
∧
(T in °C, T in K), C ist der bewölkte Anteil des Himmels, eA der Sättigungsdampfdruck bei Tair (in
mbar), eS der Sättigungsdampfdruck bei Tsurf (in mbar), a, b und c sind Koeffizienten für ein geeignetes
Temperaturintervall (=6.1121, 17.502, 240.97), u10 und u8 die Windgeschwindigkeit in 10m und 8m
Höhe (in ms-1), LV ist die latente Wärme der Evaporation und Bowen die druckkorrigierte BowenKonstante (=0.61·Luftdruck).
Formel 3 stammt aus der Arbeit von Henderson-Sellers (1986), Formel 4 aus Livingstone und
Imboden (1989), Formel 5 aus Brutseart (1975) zit. n. Livingstone und Imboden (1989), Formel 6 aus
Idso und Jackson (1969) zit. n. Henderson-Sellers (1986), Formel 7 aus Henderson-Sellers (1986),
Formel 8 aus McMillan (1971) zit. n. Livingstone und Imboden (1989), Formel 9 aus Dake (1972),
Formel 10 aus Buck (1981) und Formel 11 aus Henderson-Sellers (1986).
In der Berechnung wird die Oberflächentemperatur Tsurf der Gleichgewichtstemperatur Teq
gleichgesetzt. Der beschriebene Formelsatz (ausgenommen die alternativen Formeln EA_alt und HV_alt)
wird für alle Berechnungen verwendet, sofern nichts anderes deklariert wird. Diese Formeln werden in
dieser Arbeit künftig als Standardformeln beschrieben. Die von den einzelnen Standardformeln
errechneten Wärmeflüsse befinden sich ungefähr im Mittelfeld im Vergleich mit anderen
entsprechenden Formeln. Die alternativen Formeln der Wärmeflüsse ergeben hingegen deutlich überoder unterdurchschnittliche Energietransfers.
Die alternativen Formeln für die atmosphärische Emissivität und den latenten Wärmefluss werden
dazu benützt, die Sensitivität der Resultate auf die Verwendung unterschiedlicher Formeln der
Wärmeflüsse abzuschätzen. Die atmosphärische Emissivität wie auch der latente Wärmefluss lassen
sich durch eine grosse Anzahl verschiedener Formeln beschreiben. Zudem haben sie grossen Anteil
am gesamten Energieaustausch zwischen Seeoberfläche und Atmosphäre. Die alternativen Formeln
wurden jeweils so gewählt, dass sie sich stark von der anderen Formel desselben Wärmeflusses
unterscheidet.
14
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
Die in dieser Arbeit verwendeten Formeln für die Wärmeflüsse beziehen sich auf offene
Wasserflächen. Bei Gefrier- und Schmelzprozessen sowie über Eis wäre der Formelsatz anzupassen.
Deshalb werden Datenpunkte nicht berücksichtigt, bei welchen die Gleichgewichtstemperatur in den
Berechnungen unter 0°C zu liegen kommt. Dennoch kann Eis bei Monaten mit tiefen
Gleichgewichtstemperaturen gewisse Unsicherheiten und Ungenauigkeiten verursachen. Auch wenn
die monatlich gemittelte Gleichgewichtstemperatur über 0°C liegt, kann während Teilen des Monates
eine Eisbedeckung bestanden haben. Bei sehr tiefen Gleichgewichtstemperaturen ist deshalb mit
einigen Ungenauigkeiten zu rechnen.
Der grösste Teil des Wärmeaustausches zwischen Wasseroberfläche und Atmosphäre findet in einer
sehr dünnen Grenzschicht statt. Für die langwellige Ein- und Ausstrahlung sowie die turbulenten
Wärmeflüsse sind die obersten 1-2mm des Wasserkörpers entscheidend (McAllister and McLeish,
1969 zit. n. Henderson-Sellers, 1986). Die solare Einstrahlung hingegen kann in tiefere Schichten
eindringen und somit eine grössere Verteilung der Energie bewirken. Der Teil der nicht an der
Oberfläche absorbierten Strahlung kann je nach Trübung in grössere Tiefen eindringen und das
Wasser unter der Oberflächenschicht direkt erwärmen (Henderson-Sellers, 1986). Nach verschiedenen
Autoren werden ca. 40-50% der totalen Energie der solaren Einstrahlung in den obersten Millimetern
absorbiert (Henderson-Sellers, 1986). In den meisten Fällen wird die gesamte Energie der
Wärmeflüsse in der durchmischten Oberflächenschicht absorbiert. In sehr klaren Seen könnte ein Teil
der Energie der solaren Einstrahlung allerdings unter der durchmischten Oberflächenschicht deponiert
werden. Dies würde zu Ungenauigkeiten in der berechneten Gleichgewichtstemperatur führen, da die
Berechnung von der gesamten Energieaufnahme der solaren Einstrahlung ausgeht.
2.2.1 Vertieftere Ausführungen zu einigen Wärmeflüssen
2.2.1.1 Solare Einstrahlung
Um die vom Wasserkörper absorbierte Energie der solaren Einstrahlung zu bestimmen, muss das
Rückstreuungsvermögen (Albedo) der Wasseroberfläche bekannt sein (Gleichung 3). Die Albedo von
Seen ist zeitlich und räumlich variabel. Sie ist eine Funktion des Einfallswinkels der Strahlung und des
Zustandes der Wasseroberfläche (z.B. Wellenhöhe, suspendiertes Material) (Henderson-Sellers, 1986).
Gemäss Nunez et al. (1972) ist neben dem Einfallswinkel die Art der Strahlung (direkt oder diffus)
entscheidend, von den Oberflächeneigenschaften hat einzig der Wellengang signifikanten Einfluss. So
sind denn auch die Reflektionseigenschaften verschiedener Wasserkörper konsistent (Nunez et al.,
1972). Die Unterschiede der Albedo bei direkter und diffuser Einstrahlung können markant ausfallen.
Globale Durchschnittswerte der Albedo wurden von verschiedenen Autoren auf 0.06 und 0.08
15
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
geschätzt (Henderson-Sellers, 1986). Für räumlich-zeitliche Untersuchungen globaler Grössenordnung
ist die Verwendung eines globalen Mittelwertes ungenügend. Klimamodelle stellen Daten der totalen
solaren Einstrahlung an der Erdoberfläche bereit (HS0, in Wm-2), unterscheiden aber nicht zwischen
direkter und diffuser Einstrahlung.
Ein Modell zur Berechnung monatlich gemittelter globaler Albedo-Werte existierte bisher nicht. Ein
solches Modell musste deshalb entwickelt werden.
Anteil direkter und diffuser Strahlung an gesamten solaren Einstrahlung
In einem ersten Schritt soll der Anteil der direkten und diffusen Strahlung an der totalen Einstrahlung
abgeschätzt werden. Diffuse Strahlung wird überwiegend durch Bewölkung erzeugt. Der
Bewölkungsanteil (C) wird deshalb als Schätzfunktion der diffusen Einstrahlung verwendet. Die
Unterschiede der Abdunkelungseffekte durch Bewölkung sind je nach Wolkentyp- und Dichte enorm.
Franceschini (1968) ermittelte eine durchschnittliche Abdunkelung von 18% bei Zirren und 85% bei
Kumulonimben. Caskey (1945) berechnete die globale durchschnittliche Wolkenalbedo auf 0.63 und
erwähnt die Resultate anderer Studien mit Werten von 0.47 und 0.6. Aufgrund der grossen Streuungen
kann nur ein ungefährer Mittelwert der wolkenbedingten Abdunkelung gewählt werden. Dieser Wert
wurde hier auf 50% festgelegt. Der Anteil direkter und diffuser Strahlung an der Gesamteinstrahlung
kann nun als Funktion der Bewölkung ausgedrückt werden (Abb. 3).
Anteil diffuser an gesamter
Solarstrahlung
1
0.8
0.6
0.4
0.2
0
0
0.2
0.4
0.6
0.8
1
Bewölkungsanteil
Abb. 3. Anteil diffuser Strahlung an gesamter Solarstrahlung als Funktion der Bewölkung. Der Anteil direkter
Strahlung bildet die Differenz zwischen gesamter und diffuser Strahlung.
Direkte solare Einstrahlung
Die auf die Erdoberfläche eintreffende solare Strahlung ist nie vollkommen gerichtet. Auch bei
wolkenfreien Verhältnissen gibt es immer eine diffuse Komponente der totalen Strahlung (Cogley,
1979; Franceschini, 1968). Gemäss Cogley (1979) präsentiert die Arbeit von Grishchenko (1959) gute
Werte der Albedo, welcher mit über 200 vorsichtigen Messungen bei Einfallswinkeln von 0° bis 70°
ermittelt wurden. Diese Daten beziehen sich auf Wellenhöhen von 0.1–0.7m und Bewölkungsanteile
16
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
von 0-25%. Sie eignen sich als Normalwerte bei Schönwetter-Bedingungen und sind für grossskalige
Studien besser geeignet als andere Ansätze (Cogley, 1979). Verschieden Studien weisen darauf hin,
dass sich die Albedo bei sehr tiefem Sonnenstand sich nicht 1 annähert, sondern bei Einfallswinkeln
von weniger als ca. 10° rapide abnimmt (Henderson-Sellers, 1986). Dieser Effekt wird bei
Grishchenko (1959) gut wiedergegeben und ist auf den grossen Anteil der diffusen Komponente der
Einstrahlung bei kleinen Einfallswinkeln zurückzuführen (Cogley, 1979). Die Albedo-Werte nach
Grishchenko sind in tabellarischer Form (alle 10° Breite ein monatlich gemittelter Messwert) in der
Arbeit von Cogley (1979) wiedergegeben. Diese Messwerte werden entlang der Breite interpoliert. Bei
Verwendung dieser Daten wird den räumlich-zeitlichen Fluktuation der Albedo Rechnung getragen.
Diffuse solare Einstrahlung
Unter diffuser Strahlung ist die Albedo von Wasser nahezu konstant (Cogley, 1979). Die
Abhängigkeit der Albedo vom Einfallswinkel der Solarstrahlung kann demnach bei diffuser Strahlung
vernachlässigt werdend. Die Albedo wird bei sehr kleinen Zenitwinkeln der Sonneneinstrahlung durch
Bewölkung erhöht und bei grossen Zenitwinkeln verkleinert (Nunez et al., 1972). Die Albedo einer
Wasseroberfläche liegt bei diffuser Strahlung gemäss Cogley (1979) bei 0.06-0.01, Nunez et al. (1972)
ermittelten bei Messungen auf dem Ontario-See Werte von 0.074-0.082 und Burt (1953) (zit. n.
Nunez, 1972) errechnete den theoretischen Wert von 0.066. In dieser Arbeit wird der letztgenannte
Wert für die Albedo des diffusen Strahlungsanteils verwendet.
Berechnung der ins Wasser eindringenden solaren Einstrahlung
Die im Wasserkörper absorbierte Solarstrahlung HS wird nun mit folgenden Gleichungen berechnet:
H S = H S 0 ⋅ FG _ dir ⋅ (1 − Adir ) + H S 0 ⋅ FG _ diff ⋅ (1 − Adiff )
FG _ dir = (1 − C ) ⋅
FG _ diff =
C
⋅
2
1
(12)
(13)
C
(1 − C ) +
2
1
(14)
C
(1 − C ) +
2
Dabei ist HS0 die Solarstrahlung über der Wasseroberfläche, FG_dir und FG_diff sind die
Gewichtungsfaktoren für den Anteil direkter resp. diffuser Strahlung an der Gesamtstrahlung, Adir und
Adiff sind die Albedo für direkte resp. diffuse Strahlung und C ist der Bewölkungsanteil.
17
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
Gleichung 12 erlaubt die Berechnung der vom Wasserkörper absorbierten solaren Einstrahlung
entsprechend der orts- und zeitabhängigen Albedo.
Abb. 4. zeigt die jährlich gemittelte Albedo von Seeoberflächen am Beispiel von CNRM-Klimadaten
der Zeitperiode 1961-1990. Zonen reduzierter Albedo in hohen Breiten wegen grösserem diffusen
Strahlungsanteil sind gut ersichtlich. Die globalen Mittelwerte der Albedo über Landoberflächen
liegen bei allen Klimamodelldaten im oberen Bereich oder leicht über den von anderen Autoren
beschriebenen Albedo-Werten von 0.6-0.8. Der flächengewichtete Mittelwert bei Verwendung von
CNRM-Basisklimadaten liegt z.B. bei 0.82. Die höheren Albedo-Werte sind allerdings plausibel, da
über Ozeanen häufiger eine Wolkendecke liegt als über Landoberflächen. Dies hat ein höherer Anteil
diffuser Strahlung zur Folge, was in den meisten Fällen zu einer Verringerung der Albedo führt. Wird
die Albedo über dem ganzen Globus (Land und Meer) berechnet, sind die Resultate im Einklang mit
den von anderen Autoren ermittelten Grössen (z.B. Albedo über dem gesamten Globus mit CNRMBasisklimadaten: 0.75).
b)
a)
Abb. 4. Jährlich gemittelte Albedo am Beispiel von CNRM-Basisklimadaten a) an jedem Punkt der
Landoberfläche und b) entlang der geographischen Breite über Landoberflächen. In a) beschreiben negative
Werte der Y-Achse die südlichen Breitengrade, positive die nördlichen. Auf der X-Achse werden Längengrade
beschrieben, beginnend beim Nullmeridian. Die Datenlücke bei b) um 60° Süd ist auf die Absenz von
Landmasse zurückzuführen.
2.2.1.2 Langwellige Einstrahlung
Die langwellige Einstrahlung ist der schwierigste Term der Energiebilanzgleichung (Gleichung 4) und
ist am anfälligsten auf Berechnungsfehler (Livingstone and Imboden, 1989). Die einfallende
langwellige Strahlung entsteht als Emission von Molekülen in verschiedenen Atmosphärenschichten
(Henderson-Sellers, 1986). Hauptverantwortlich für diese Emissionen sind CO2 und Wasserdampf
sowie das flüssige Wasser in Wolken (Henderson-Sellers, 1986). Der Einfluss des Menschen auf das
18
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
Klima betrifft vor allem die langwellige Einstrahlung durch die Erhöhung atmosphärischer
Treibhausgaskonzentrationen.
Beide Formeln der atmosphärischen Emissivität (Formeln 5 und 6) benötigen Daten der
Lufttemperatur
in
2m
Höhe.
Gemäss
Henderson-Sellers
(1986)
ist
es
sinnvoll,
die
Emissionstemperatur der Temperatur der tiefsten Atmosphärenschicht gleichzusetzen, da Emissionen
aus grosser Höhe die Wasseroberfläche kaum ohne Reabsorption und Reemission erreichen. Die
Formel der atmosphärischen Emissivität nach Brutsaert (Formel 5) basiert auf physikalischen
Eigenschaften der Atmosphäre, während die Formel nach Idso und Jackson (Formel 6) empirisch
ermittelt wurde. Formel 5 integriert den Dampfdruck, während dieser Parameter nicht in Formel 6
einfliesst. Aufgrund des starken Effektes von Wasserdampf auf die Emissivität der Atmosphäre (siehe
Kapitel 2.3.2) ist der Ansatz von Idso and Jackson in Frage zu stellen. Dennoch stimmt diese Formel
gemäss verschiedenen Studien besser mit Beobachtungen im Feld überein als ähnliche, häufig
verwendete Formeln (Henderson-Sellers, 1986). Für beide Formeln zur Berechnung der
atmosphärischen
Emissivität
wurde
ein
von
Henderson-Sellers
(1986)
beschriebener
2
Multiplikationsfaktor (1+0.17·C ) eingeführt. Damit wird der Einfluss der Bewölkung in die sonst für
wolkenfreie Verhältnisse konzipierten Formeln integriert.
Die Temperaturabhängigkeit der atmosphärischen Emissivität ist bei Verwendung der Formel 5
(Brutsaert) ausgeprägt, während die atmosphärische Emissivität bei Formel 6 (Idso and Jackson)
nahezu eine konstante, temperaturunabhängige Grösse bildet (Abb. 5). Bei hoher Lufttemperatur und
Luftfeuchtigkeit liefert Formel 5 viel höhere Emissionswerte als Formel 6, bei tiefer Temperatur und
Luftfeuchtigkeit ist es umgekehrt.
19
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
Abb. 5. Vergleich verschiedener Formeln zur Berechnung der atmosphärischen Emissivität. Die Emissivität wird
als Funktion der Temperatur bei drei verschiedenen Konzentrationen der relativen Feuchtigkeit dargestellt.
Während die bei Brutsaert eine starke Abhängigkeit von Temperatur und Luftfeuchtigkeit auszumachen ist,
beschreibt die die Formel nach Idso and Jackson nahezu eine Konstante. Die Kurve dieser Formel ist etwas
unsauber wiedergegeben. Da sie unabhängig von der Luftfeuchtigkeit ist, müssten die Kurven bei allen relativen
Luftfeuchtigkeiten identisch sein (Henderson-Sellers, 1986).
20
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
2.2.1.3 Latenter Wärmefluss
Der latente Wärmefluss kann durch Evaporation zu einem Energieverlust und durch Kondensation zu
einem Energiezuwachs an der Wasseroberfläche führen. Es gibt eine Vielzahl an Formeln, welche den
latenten Wärmefluss beschreiben. Eine Ursache dafür sind die zahlreichen Windfunktionen, welche
meist auf empirischen Beobachtungen beruhen (Henderson-Sellers, 1986). Wind beeinflusst die
Evaporationsrate durch die Erneuerung der Luftmassen. Wenn eine Luftmasse mit einer Wasserfläche
in Kontakt kommt, evaporiert Wasser in die Luftmasse und die relative Feuchte steigt (HendersonSellers, 1986). Dies bewirkt eine Abnahme der Effizienz der Absorbierung von Wasserdampf
(Henderson-Sellers, 1986).
Als alternativer Ansatz zur Berechnung des latenten Wärmeflusses wurde die Formel von Meyer für
kleine Seen gewählt (Formel 9). Im Gegensatz zur Formel nach McMillan (Formel 8) fehlt hier der
Term zur Berücksichtigung der atmosphärischen Stabilität (0.26·(Tsurf-Tair)). Die Formel berechnet nur
die evaporierte Wassermasse und muss deshalb noch mit der Verdampfungswärme (LV) multipliziert
werden. Diese ist eine schwache Funktion der Wassertemperatur (Edinger et al., 1968; HendersonSellers, 1986). Nach Henderson-Sellers (1986) kann die Verdampfungswärme (LV) beschrieben
werden als
∧
∧
LV (T ) = 1.91846 ⋅ 10 ⋅
T surf
6
∧
∧
(T surf − 33.91)
(15)
2
∧
wobei T die Lufttemperatur (in K) ist und Tsurf die Seeoberflächentemperatur (in K).
Da Formel 9 mit Winddaten einer Höhe von 8m berechnet wird, müssen die Daten der Klimamodelle
(Windgeschwindigkeit auf 10m Höhe) angepasst werden. Die Windgeschwindigkeit nimmt mit
geringerer Höhe aufgrund der Reibung an der Wasseroberfläche ab. Dies wird mit dem sogenannten
Wandgesetz von Israelsen und Hansen (1965) (zit. n. Dake, 1972) durchgeführt. Die
Windgeschwindigkeit auf 8m Höhe (u8) ist gegeben durch
u 8 = u10 ⋅
log 8
log 10
(16)
wobei u10 die Windgeschwindigkeit in 10m Höhe ist (in ms-1).
Die Formel nach McMillan wie auch die von Meyer wurden empirisch entwickelt. Die Formel von
Meyer führt zu einem bedeutend stärkeren latenten Wärmefluss (Abb. 6). Meyers Formel weist im
Vergleich mit anderen Ansätzen sowohl bei negativen wie auch positiven Energieflüssen hohe Werte
21
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.2 Wärmeflüsse
auf. Der Ansatz von Penman überschätzt die latenten Wärmeflüsse und ist ungeeignet für Studien,
welche verschiedene Klimate umfassen (Henderson-Sellers, 1986).
a)
b)
Abb. 6. Vergleich verschiedener Formeln des latenten Wärmeflusses für die Klimatologie von a) Grossbritannien
und b) Südafrika. Die Werte von MacMillan liegen etwa im Mittelfeld, währen bei Meyer stets
überdurchschnittliche Werte auftreten (Henderson-Sellers, 1986).
22
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.3 Klimafaktoren
2.3 Klimafaktoren
Für die Wärmeflüsse durch die Wasser-Luft-Grenzschicht sind einzelne Klimafaktoren verantwortlich.
Wie sich veränderte Klimafaktoren genau auf die Energieflüsse auswirken, ist schwierig zu eruieren.
Aus diesem Grund gibt es eine Vielzahl an Formeln zur Berechnung des Energieaustausches und nicht
einzelne „richtige“. Klimafaktoren beeinflussen sich gegenseitig (Livingstone and Imboden, 1989;
Randall et al., 2007). Diese Zusammenhänge sind sehr komplex und teilweise noch wenig verstanden.
Die einzelnen Klimafaktoren und deren Auswirkungen auf die Gleichgewichtstemperatur soll
nachfolgend besprochen werden.
2.3.1 Lufttemperatur
Die Lufttemperatur beeinflusst die langwellige Einstrahlung sowie die turbulenten Wärmeflüsse. Das
Verhältnis zwischen Luft- und Wassertemperatur wurde in diversen Studien untersucht. Viele davon
beschreiben einen starken Zusammenhang zwischen diesen beiden Parametern (z.B. Arnott et al.,
2003; Mooij, 2005; Mohseni and Stefan, 1999). Bei steigender durchschnittlicher Lufttemperatur
nimmt die durchschnittliche Wassertemperatur generell mit einer kleineren Rate zu (Croley II, 1990).
Mohseni and Stefan (1999) beschrieben diesen Zusammenhang bei tiefen und moderaten
Lufttemperaturen als linear, unter 0°C und über 20°C flacht die Steigung der Kurve allerdings
signifikant ab. Bei steigender Lufttemperatur vergrössert sich das Damfdruckdefizit über der
Wasseroberfläche drastisch, was zu einer starken evaporativen Abkühlung führt und somit die
Beziehung zwischen Wasser- und Lufttemperatur abschwächt (Mohseni and Stefan, 1999). Dies ist der
Hauptgrund für die Nichtlinearität von Luft- und Wassertemperatur (Mohseni and Stefan, 1999).
Studien zur Bestimmung der Oberflächenwassertemperatur anhand der Lufttemperatur wurden
deshalb überwiegend in Seen gemässigter Klimate durchgeführt. Wasser- LufttemperaturZusammenhänge sind immer an eine bestimmte Lokalität gebunden. Des Weiteren können die
Zusammenhänge der Luft- Wassertemperatur unter veränderten Klimabedingungen ihre Gültigkeit
verlieren. Gemäss Bogan et al. (2003) ist die Gleichgewichtstemperatur deshalb besser zur
Beschreibung der Oberflächen-Wärmeflüsse geeignet als die Lufttemperatur.
2.3.2 Dampfdruck
Die Luftfeuchtigkeit beeinflusst als das wichtigste Treibhausgas (Randall et al., 2007) die Emissivität
der Atmosphäre sowie den latenten Wärmefluss. Der atmosphärische Wassergehalt ist stark
23
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.3 Klimafaktoren
temperaturabhängig, da der Sättigungsdampfdruck bei steigender Lufttemperatur exponentiell
zunimmt. Der evaporative Energieverlust ist abhängig vom Dampfdruckdefizit (Differenz von
Sättigungsdampfdruck und effektivem Dampfdruck). Dieser kann nur bei hohen Temperaturwerten
grosse Werte erreichen, grosse Energieumsätze durch Evaporation sind demnach auf tiefere Breiten
beschränkt. Anders verhält es sich beim Effekt der Absorption langwelliger Strahlung durch
Wasserdampf. Dieser Effekt ist ungefähr proportional zum Logarithmus der Dampfdruckkonzentration
(Randall et al., 2007). Es ist also die anteilmässige und nicht die absolute Änderung des
Dampfdruckes, welche die Stärke des langwelligen Rückstreuungseffektes ausmacht (Randall et al.,
2007). Im Normalfall wird davon ausgegangen, dass die relative Luftfeuchtigkeit bei einem
Temperaturanstieg etwa konstant bleibt (Randall et al., 2007). Aufgrund des so erhöhten
Dampfdruckes verstärkte sich die langwellige Einstrahlung. Diese sogenannte WasserdampfRückkoppelung ist der wichtigste Rückkoppelungsprozess in der Erhöhung der Klimasensitivität
(Randall et al., 2007). Sie bewirkt eine Verstärkung der globalen Lufttemperaturerwärmung von rund
50% bei einem Gradienten von ca. 1 Wm-2 °C-1 (Randall et al., 2007).
Der Klimawandel beeinflusst auch die Hydrologie. Das Klima kann durch räumliche Veränderungen
des Niederschlages regional zu trockeneren oder feuchteren Verhältnissen führen. In solchen Fällen
kann nicht von einer konstanten relativen Luftfeuchtigkeit ausgegangen werden. Wird z.B. das Klima
in einer Region ganzjährig oder jahreszeitlich deutlich arider, ist aufgrund grossflächig verminderter
evaporativer Kühlung mit einem Anstieg der Lufttemperatur und einer gleichzeitigen Abnahme der
Luftfeuchtigkeit zu rechnen.
2.3.3 Windgeschwindigkeit, Bewölkung und solare Einstrahlung
Die
Windgeschwindigkeit
beeinflusst
die
Stärke
der
turbulenten
Wärmeflüsse.
Hohe
Windgeschwindigkeiten verstärken positive wie auch negative Energieflüsse. Neben der
Beeinflussung der Wärmeflüsse ist die Windstärke hauptverantwortlich für die Tiefe der
durchmischten
Oberflächenschicht
des
Sees.
Damit
beeinflusst
die
Windstärke
die
Wärmespeicherkapazität des Epilimnions und damit das Verhältnis zwischen Oberflächentemperatur
des Wassers und Gleichgewichtstemperatur.
Bewölkung
erhöht
die
atmosphärische
Emissivität
und
beeinflusst
die
Albedo
von
Gewässeroberflächen. Die Bewölkung hat durch Abdunkelungseffekte starken Einfluss auf die an der
Erdoberfläche eintreffende Solarstrahlung. Dieser Effekt der Bewölkung wird in dieser Arbeit
vernachlässigt, da er im Faktor der solaren Einstrahlung impliziert ist. Die Modellierung der
zukünftigen Entwicklung der Bewölkung und das Verständnis von Rückkoppelungseffekten mit dem
Klima sind noch wenig entwickelt (z.B. Randall et al. 2007).
24
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.4 Statistik
Die solare Einstrahlung an der Atmosphärenoberfläche kann als konstant betrachtet werden. Zwar gibt
es Schwankungen der Solarkonstanten, diese liegen aber mit Periodendauern von mehreren
zehntausenden von Jahren weit über dem untersuchten Zeitraum von etwas mehr als 100 Jahren und
sind deshalb irrelevant. Der 11-jährige Sonnenfleckenzyklus liegt innerhalb der 30-jährigen
klimatischen Mittelwerte, zudem sind diese zyklischen Schwankungen sehr gering. Gewisse
Klimamodelle berücksichtigen die geringe Variabilität der Solarkonstanten. Wichtig für die von einer
Wasseroberfläche aufgenommene Energie der solaren Strahlung ist neben dem Einstrahlungswinkel
und der Strahlungsdauer die Albedo des Wasserkörpers und vor allem der Zustand der Atmosphäre.
Die Bewölkung hat den grössten Verminderungseffekt auf die atmosphärische Transparenz.
Allerdings ist die solare Einstrahlung nicht nur eine Funktion der Bewölkung. Die atmosphärische
Transparenz wird auch von anderen Parametern wie der Konzentration an Aerosolen oder von Dunst.
beeinflusst.
2.4 Statistik
Klimaparameter interagieren über verschiedene Wege miteinander. Deshalb sollten die Effekte von
Fluktuationen der Klimafaktoren auf die Gleichgewichtstemperatur nicht als unabhängig voneinander
betrachtet werden (Livingstone and Imboden, 1989). Gemäss Randall et al. (2007) beeinflussen sich
Dampfdruck, Bewölkung und Lufttemperatur stark gegenseitig. Zur Eischätzung der Stärke der
gegenseitigen Beeinflussung einzelner Klimafaktoren wurden immer zwei Faktoren auf ihre
Korrelation geprüft. Dazu wurden die Anomalien zwischen zukünftigem Klima und Basisklima der
CNRM-Klimadaten verwendet. Es wurden alle Daten verwendet, welche in die Berechnung der
Gleichgewichtstemperatur
einfliessen
(alle
Datenpunkte
über
Land
mit
einer
Gleichgewichtstemperatur über 0°C). Der stärkste Zusammenhang wurde mit einer negativen
Korrelation zwischen Anomalien der Bewölkung und der solaren Einstrahlung ermittelt. Der
Zusammenhang lässt sich gut linear beschreiben bei einer Verringerung der solaren Einstrahlung von
1.4 Wm-2 pro 1% Zunahme des Bewölkungsanteils. Das R2 liegt bei 0.62. Dampfdruck- und
Lufttemperaturanomalien korrelieren bei tiefen absoluten Lufttemperaturen stark, bei höheren
Lufttemperaturen ist kaum eine Korrelation vorhanden. Andere Faktorkombinationen zeigen nur
wenig eindeutige Korrelationen. Wie das Beispiel der Korrelation von Luft- und DampfdruckAnomalie zeigt, können die Zusammenhänge räumlich stark variieren.
25
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.4 Statistik
Die Gleichgewichtstemperatur wird über Energiebilanzgleichungen aus Klimafaktoren berechnet und
ist somit völlig abhängig von diesen. Veränderungen der Gleichgewichtstemperatur sind somit durch
Fluktuationen der Klimafaktoren erklärbar. Es kann also geschrieben werden
dTeq = f (dTair , de A , du , dC , dH S ) + ε
(17)
wobei Teq die Gleichgewichtstemperatur, Tair die Lufttemperatur, eA die Luftfeuchtigkeit, u die
Windgeschwindigkeit, C den Bewölkungsgrad, HS die solare Einstrahlung und ε den Fehlerterm
bezeichnen. d steht jeweils für die Anomalie des Parameters.
Der Einfluss von veränderten Klimafaktoren auf die Oberflächentemperatur von Seen soll mit Hilfe
statistischer Mittel bestimmt werden. Es soll gezeigt werden, wie stark die Gleichgewichtstemperatur
auf die Änderung einer Einheit der verschiedenen Klimafaktoren reagiert. Wären die Klimafaktoren
untereinander unkorreliert, könnte zur Bestimmung der Abhängigkeit der Gleichgewichtstemperatur
von den Klimafaktoren Einzelregressionen durchgeführt werden. Da dies nicht der Fall ist, wird
stattdessen mit multipler Regression gearbeitet. Dabei sind die Klimafaktoren die unabhängigen
Variablen während die Gleichgewichtstemperatur die abhängige Variable darstellt. In der multiplen
Regression werden auch die Zusammenhänge der unabhängigen Variablen untereinander beachtet. Die
Regressionsgleichung lautet in diesem Fall:
dTeq = β 0 + β 1 ⋅ dTair + β 2 ⋅ de A + β 3 ⋅ du + β 4 ⋅ dC + β 5 ⋅ dH S + ε
(18)
Nun können die Koeffizienten β1 bis β5 und damit der lineare Zusammenhang zwischen
Gleichgewichtstemperatur und den Klimafaktoren bestimmt werden (Kapitel 3.5.2). Da die
Gleichgewichtstemperatur ohne die Änderung eines Klimafaktors konstant bleibt, ist β0 = 0.
Die Linearität der ermittelten Zusammenhänge ist nicht immer gegeben. Teilweise könnten mit
nichtlinearen Regressionen bessere Resultate erzielt werden. Auf derartige tiefergreifende statistische
Untersuchungen wird in dieser Arbeit aber verzichtet.
Eine gewisse Korrelation unter den unabhängigen Variablen ist bei der multiplen Regression
unproblematisch. Werden gewisse Korrelationen aber zu stark, kann das Fehler in den Resultaten
hervorrufen. Dies ist in Einzelfällen bei den Resultaten regionaler Skala der Fall. Die Resultate der
Regressionsanalyse soll deshalb kritisch beurteilt werden.
26
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.5 Klimamodelle
2.5 Klimamodelle
In der aktuellen Erforschung des Klimasystems und des Klimawandels sind Klimamodelle ein
zentrales Instrument. Sie basieren auf gut etablierten physikalischen Grundlagen und sind in der Lage,
das heutige Klima wie auch vergangene Klimaänderungen zu reproduzieren (Randall et al., 2007). In
Klimamodellen werden Atmosphären- und Ozeanzirkulationsmodelle gekoppelt, weshalb von
AOGCMs (Atmosphere-Ocean General Circulation Models) gesprochen wird. Diese sind das am
weitesten entwickelte Mittel, um das Verhalten des globalen Klimasystems zu erfassen (Christensen et
al., 2007; Randall et al., 2007) und um Klimawandelszenarien zu modellieren (Mortsch and Quinn,
1996). Somit bieten Klimamodelle die besten erhältlichen Informationen, um die Auswirkungen des
Klimawandels auf die Wasserqualität und die Ökologie von Oberflächengewässern abzuschätzen
(Whitehead et al., 2009). Da Klimamodelle hochkomplex sind, können ihre Codes nur auf
leistungsstarken Grosscomputern durchgeführt werden. Trotz ihrer grossen Komplexität sind
Klimamodelle noch immer eine grobe Repräsentation des realen Klimasystems und werden limitiert
durch das Verständnis von Klimaprozessen und Rückkoppelungsmechanismen (Mortsch and Quinn,
1996). In den vergangenen Jahren wurden Klimamodelle allerdings stark weiterentwickelt und in
vielen Bereichen wurden wichtige Verbesserungen erzielt. Heute sind einige AOGCMs beispielsweise
in der Lage, wichtige Aspekte der El Niño-Southern Oscillation (ENSO) wiederzugeben (Randall et
al., 2007). Der Entwicklungstrend der globalen Temperatur im vergangenen Jahrhundert kann unter
Einbezug anthropogener und natürlicher klimabeeinflussender Faktoren sehr gut modelliert werden
(Randall et al., 2007).
2.5.1 Emissionsszenarien
Mit AOGCMs können die Auswirkungen von externen Einflussfaktoren auf das Klimasystem
untersucht werden. Der aktuelle Klimawandel ist grösstenteils bedingt durch den Anstieg
atmosphärischer Treibhausgase. Entscheidend ist demnach, von welcher Entwicklung der
Treibhausgasemissionen ausgegangen wird. Im Rahmen der Studien des IPCC wurden verschiedene
Emissionsszenarien entwickelt (z.B. Meehl et al., 2007). Zukünftige Emissionen klimarelevanter
Stoffe sind von diversen Faktoren abhängig. Dazu gehören die Entwicklungen im Bereich Ökonomie,
Technik, Politik und Bevölkerungswachstum. In dieser Arbeit wird von dem Szenario SRES (Second
Report on Emission Szenarios) A1B ausgegangen. Die Hauptannahmen dieses Szenarios werden
beschrieben als "A future world of very rapid economic growth, low population growth and rapid
introduction of new and more efficient technology. Major underlying themes are economic and
cultural convergence and capacity building, with a substantial reduction in regional differences in per
27
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.5 Klimamodelle
capita income. In this world, people pursue personal wealth rather than environmental quality”
(IPCC Data Distribution Centre). Eine solche Entwicklung bewirkt im Vergleich mit anderen
Emissionsszenarien einen mittleren Ausstoss an Treibhausgasen (Meehl et al., 2007). Die SRESSzenarien berücksichtigen den anthropogen bedingten Ausstoss der strahlungsrelevanten Stoffe CO2,
CH4, N2O, Chlor-Fluor-Karbonate sowie SO2 (als Aerosol in Form von Sulfat (SO4)) (Meehl et al.,
2007). Es gibt allerdings weitere Faktoren, welche die Entwicklung des Klimas beeinflussen. Es wurde
den individuellen Modellierungsgruppen überlassen, zusätzlich die künftige Entwicklung von
troposphärischem und stratosphärischem Ozon, allen nicht-sulfatischen Aerosolen, indirekten Effekten
der Aerosole auf die Wolkenalbedo und Lebensdauer, Landnutzungsänderungen sowie Variabilitäten
der Solarstrahlung abzuschätzen und in die AOGCMs zu integrieren (Meehl et al., 2007). Die
Differenzen der globalen Erwärmung bei Einsatz verschiedener Emissionsszenarien nehmen mit
steigender Zeitdauer zu und fallen bei Modellierungen für das Ende dieses Jahrhunderts sehr stark aus
(Meehl et al., 2007).
Das Klima des vergangenen Jahrhunderts kann von Klimamodellen mit dem „20th Century
Experiment (20C3M)“ modelliert werden. Dabei werden die Berechnungen unter den gemessenen
anthropogenen wie auch natürlichen (z.B. Vulkanausbrüche) klimarelevanten Faktoren des 20.
Jahrhunderts durchgeführt (Meehl et al., 2007).
2.5.2 Güte der Klimamodelle
Klimamodelle wurden in den vergangenen Jahren in diversen Studien untersucht und ausführlich auf
ihre Zuverlässigkeit getestet. Gemäss Randall et al. (2007) kann Klimamodellen hauptsächlich
aufgrund ihrer physikalischen Grundlagen und ihren Fähigkeiten, aktuelles Klima wie auch
vergangene Klimaänderungen zu simulieren (z.B. glaziales Maximum vor 21000 Jahren) vertraut
werden.
Die Unsicherheit in der Prognostizierung des künftigen Klimas hat grundsätzlich zwei verschiedene
Hauptursachen. Zum einen ist die Entwicklung von Treibhausgasemissionen und anderer
klimarelevanter Stoffe schwer abschätzbar (Abb. 7, 1. Schritt). Emissionsszenarien können nicht als
richtig oder falsch bewertet werden, sie zeigen bloss die Emissionsentwicklung unter Annahme
bestimmter Bedingungen. Zum andern sind die letztendlichen Reaktionen des Klimas auf
klimarelevante Stoffe mit diversen Unsicherheiten behaftet (Abb. 7, 2.-4. Schritt). In jedem einzelnen
dargestellten Schritt liegen Unsicherheiten. Gemäss Whitehead et al. (2009) sind diese innerhalb eines
AOGCMs besonders gross im Bereich Prozessverständnis, Parametrisierung und der numerischen
Lösung der Gleichungen.
28
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.5 Klimamodelle
Abb. 7. Verschiedene Schritte von der Entwicklung der Treibhausgasemissionen bis zur Reaktion des Klimas.
Jeder Schritt ist mit Unsicherheiten verbunden. Im ersten Schritt sind diese durch Emissionsszenarien, in den
weiteren Schritten durch Klimamodelle bedingt (Meehl et al., 2007).
Besonders schwierig ist das Verständnis von Rückkoppelungen und Interaktionen verschiedener
Parameter im Klimasystem. Gemäss Randall et al. (2007) ist das schwache Wissen über BewölkungsRückkoppelungen sowie die Schwierigkeit der Modellierung von Bewölkung die primäre Quelle für
Unterschiede zwischen verschiedenen Klimamodell-Resultaten. Auch über die Stärke der
gegenseitigen Beeinflussung von Land und Atmosphäre (z.B. Bodenfeuchte-NiederschlagsRückkoppelung) herrscht Uneinigkeit (Randall et al., 2007). Gemäss Meehl et al. (2007) bewirkt
zudem die unklare zeitliche Entwicklung der wichtigsten Aerosoltypen und deren Interaktionen mit
dem Klima bedeutende Unsicherheiten in der Prognostizierung des Klimawandels. Weitere
Schwierigkeiten entstehen, da gewisse anthropogen erzeugte strahlungsbeeinflussende Faktoren das
Klima global (z.B. CO2), andere hingegen regional (z.B. Sulfat-Aerosole) beeinflussen (Christensen et
al., 2007).
Verschiedene Studien entwickelten Indizes zur Beschreibung von Klimamodellen und zur Beurteilung
der Modellgüte. Die Klimasensitivität ist ein Mass für die Reaktion des globalen Klimasystems auf
einen äusseren Einflussfaktor (Randall et al., 2007). Sie wird hauptsächlich durch interne
Rückkoppelungsprozesse bestimmt, welche den Strahlungsantrieb verstärken oder dämpfen (Randall
et al., 2007). Die Klimasensitivität einzelner Klimamodelle streut stark (z.B. Randall et al., 2007).
Gemäss Gleckler et al. (2008) gibt es keinen universellen Index, welcher die Güte eine Klimamodelles
messen könnte. Einzelne Parameter innerhalb eines AOGCMs werden im relativen Vergleich mit
anderen Modellen sehr unterschiedlich gut modelliert (Gleckler et al., 2008). Es ist grösstenteils
unbekannt, welche Aspekte des beobachteten Klimas korrekt simuliert werden müssen, damit
verlässliche Prognosen des Klimawandels gemacht werden können (Gleckler et al., 2008). Eine
markante Verkleinerung der Fehler liefert jedoch die Mittelung einer Vielzahl von Klimamodell-
29
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.5 Klimamodelle
Resultaten. Diese sogenannten Multi-Modelle übertreffen alle anderen Modelle in nahezu allen
Aspekten (Gleckler et al., 2008; Meehl et al., 2007), unter anderem weil sich Fehler einzelner Modelle
gegenseitig aufheben (Meehl et al., 2007).
2.5.3 Verwendete Klimamodelle- und Faktoren
In dieser Arbeit werden Klimadaten von 6 verschiedenen AOGCMs verwendet. Die Daten wurden im
Rahmen des 4. Klimaberichtes von IPCC berechnet. Die gewählten Klimamodelle decken eine grosse
Spannbreite an räumlicher Auflösung und Klimasensitivität von AOGCMs ab. Tab. 1. zeigt die
Originalbezeichnungen der Modelle sowie die im weiteren Verlauf der Arbeit benutzte Bezeichnung,
die räumliche Auflösung und die Urheber der Klimamodelle.
Tab. 1. Zusammenfassung der wichtigsten Daten der in dieser Arbeit verwendeten Klimamodelle.
Originalbezeichnung
Bezeichnung in
dieser Arbeit
Auflösung in
Datenpunkten
Auflösung in
Breiten- und
Längengraden
bccr_bcm2_0
BCCR
64×128
2.81°×2.81°
cccma_cgcm3_1_t63
CCCMA
48×96
3.75°×3.75°
cnrm_cm3
CNRM
64×128
2.81°×2.81°
giss_model_e_h
GISS
46×72
3.91°×5°
inmcm3_0
INMCM
45×72
4.00°×5°
miroc3.2(hires)
MIROC
160×320
1.13°×1.13°
Modellierungsgruppe
Bjerknes Centre for Climate
Research (BCCR), Univ. of
Bergen, Norway
Canadian Centre for Climate
Modelling and Analysis
(CCCma), Canada
Centre National de
Recherches Meteorologiques,
Meteo France, France
Goddard Institute for Space
Studies (GISS), NASA, USA
Institute of Numerical
Mathematics, Russian
Academy of Science, Russia
CCSR/NIES/FRCGC, Japan
Für die Berechnung der Gleichgewichtstemperatur sowie die Analyse der Resultate werden
verschieden Datensätze der AOGCMs benötigt. Die Originalbezeichnung der Datensätze sowie die
genaue Definition der Daten lautet:
• surface air temperature (tas):
Lufttemperatur 2m über Boden (K)
• surface specific humidity (huss):
Spezifische Feuchte 2m über Boden (kg/kg)
• zonal surface wind speed,
eastward wind (uas):
Windgeschwindigkeit 10m über Boden (m/s)
• meridional surface wind speed,
northward wind (vas):
• total cloud fraction (clt):
Windgeschwindigkeit 10m über Boden (m/s)
Bewölkungsanteil (%)
30
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.5 Klimamodelle
• surface downwelling shortwave
radiation (rsds):
solare Einstrahlung an der Erdoberfläche (W/m2)
• surface pressure (ps):
Oberflächenluftdruck (Pa)
• land area fraction (sftlf):
Landmaske
• surface altitude (orog):
Höhemodell (m ü. M.)
Die Auflösung der Klimadaten der verschiedenen AOGCMs unterscheidet sich teilweise beträchtlich.
Unterschiede in der Auflösung haben einen gewissen Einfluss auf die Daten. Dies soll am Beispiel der
Höhenmodelle mit der besten und der schwächsten räumlichen Auflösung gezeigt werden. Die
Topographie der Erde ist viel kleinstrukturierter und kann mit den Auflösungen der AOGCMs nur
stark vereinfacht wiedergegeben werden, was als Tiefpassfilterung wirkt. Dieser Effekt nimmt mit
abnehmender Auflösung zu und fällt somit bei dem INMCM-Modell deutlich stärker aus als bei
MIROC (Abb.7). Der höchste Punkt des INMCM-Höhenmodells liegt bei 4425m ü. M., bei den
MIROC-Daten hingegen kommt dieser Punkt bei 5565m ü. M. zu liegen. Diese Unterschiede
zwischen den verschiedenen Auflösungen kommen besonders bei flächenhaft wenig stark
ausgeprägten Gebirgszügen zur Geltung (siehe z.B. Anden). Eine solche Tiefpassfilterung tritt bei
allen Parametern auf und fällt entsprechend der Kleinräumigkeit des Parameters stärker oder weniger
stark aus.
m ü. M.
b) MIROC
m ü. M.
a) INMCM
Abb. 8. Höhenmodell des in dieser Arbeit verwendeten AOGCMs mit a) der gröbsten (INMCM) und b) der
feinsten (MIROC) räumlichen Auflösung. Alle klimatischen Faktoren der wurden durch die AOGCMs für die
entsprechende Höhe berechnet. Eine grobe Auflösung wirkt bei der kleinstrukturierten Topographie als
Tiefpassfilter.
Die Klimasensitivität des AOGCMs MIROC ist im Vergleich mit andern Klimamodellen deutlich
überdurchschnittlich, während sie z.B. bei GISS unterdurchschnittlich ausfällt (Randall et al., 2007).
Dies wirkt sich mit fortschreitender Zeit immer stärker auf die prognostizierte Erwärmung aus (Abb.
31
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.5 Klimamodelle
9). Die von MIROC simulierte Erwärmung liegt deutlich über allen andern Klimamodellen, während
bei GISS eine unterdurchschnittliche Erwärmung eintritt. Die von MIROC modellierten extremen
klimatischen Veränderungen sind auch bei der Gleichgewichtstemperatur-Anomalie ersichtlich
(Kapitel 3).
Abb. 9. Global gemittelte Erwärmung der Oberflächenlufttemperatur (Emissionsszenario SRES A1B) im
Vergleich zum Mittelwert von 1980-1999. In der Legende werden die in dieser Arbeit berücksichtigen
Klimamodelle sowie der Modell-Mittelwert aufgeführt (nach Meehl et al., 2007).
Die Güte der AOGCMs unterscheidet sich nicht nur nach einzelnen Parametern, sondern auch nach
Regionen. Gemäss Gleckler et al. (2008) modelliert CCCMA das Klima in den Tropen mit einem 5%
kleineren Fehler als der Durchschnitt einer Vielzahl an Modellen. In den Extratropen weist hingegen
MIROC besonders gute Resultate auf mit einem um 10% unterdurchschnittlichen Fehler (Gleckler et
al., 2008). Allerdings ist auch bei diesen teilweise überdurchschnittlich guten Modellen die
Spannbreite der Güte unter einzelnen Klimaparametern gross (Gleckler et al., 2008). In den Tropen
streut die Güte der Modellierung einzelner Faktoren innerhalb derselben AOGCMs besonders stark
(Gleckler et al., 2008).
32
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.6 Arbeitsschritte
2.6 Arbeitsschritte
Eine Übersicht über die durchgeführten Arbeitsschritte zur Ermittlung der Resultate bietet Abbildung
9. Wie in der Graphik dargestellt wurden die meisten Berechnungen und statistischen Auswertungen
mit dem Computerprogramm Matlab durchgeführt. Für einige Teilschritte oder Analysen wurden auch
die Programme ArcGIS und Excel eingesetzt.
GCM-Klima-Daten
(vor 2000)
GCM-Klima-Daten
(nach 2000)
MATLAB
MATLAB
monatliche Mittelwerte
2070-2099
monatliche Mittelwerte
1961-1990
Energiebilanzgleichung
an der Wasseroberfläche
MATLAB
Anomalien der Gleichgewichtstemperatur an
der Wasseroberfläche (Energiebilanz = 0)
MATLAB
Resultate (Plots, Statistiken)
Diskussion der Resultate
Abb. 10. Flussdiagramm der wichtigsten Arbeitsschritte. In den Kästchen sind die Daten zum entsprechenden
Zeitpunkt dargestellt, dazwischen wurden die Daten jeweils bearbeitet.
In einem ersten Schritt wurden die für die Berechnungen benötigten Daten bezogen. AOGCMKlimadaten sind auf der Internetseite „WCRP CMIP3 multi-model database“ des IPCC für
Forschungszwecke frei verfügbar. Die Daten liegen im NetCDF-Format vor. Gewisse Daten fehlten
allerdings und mussten direkt auf der Internetseite der entsprechenden Modellierungsgruppe bezogen
werden. Die Daten wurden als monatliche Mittelwerte bezogen. Die Daten jeden Monats wurden über
die gewünschte Dauer von 30 Jahren gemittelt (1961-1990 und 2070-2099). 30 Jahre ist die typische
Zeitperiode um Klima zu beschreiben. Kürzere Zeitperioden sind anfälliger darauf, interannuelle
Variabilitäten wiederzugeben. Die Energiebilanzgleichung mit dem gewünschten Formelsatz an
Gleichungen der Wärmeflüsse wurde in Matlab programmiert und nach der Gleichgewichtstemperatur
aufgelöst. Mit den vorhergehend erstellten Datensätzen wird die Gleichgewichtstemperatur der
Zeitperioden 1961-1990 und 2070-2099 berechnet. Alle Gleichgewichtstemperaturwerte, die 0°C
33
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
unterschritten,
wurden
aus
dem
2 Material und Methoden
2.6 Arbeitsschritte
Datensatz
entfernt.
Die
Subtraktion
der
Gleichgewichtstemperaturwerte des Basisklimas von denjenigen des zukünftigen Klimas ergibt die
Gleichgewichtstemperaturanomalie.
Die Gleichgewichtstemperaturen wurden in einem ersten Schritt über den ganzen Globus berechnet.
Daten über den Ozeanen sind allerdings nicht von Interesse. Es wurde deshalb für jedes Klimamodell
eine Land-Meer-Maske erstellt. Die mit den Klimadaten erhältlichen Daten zum Anteil der
Landoberfläche jeder Gitterzelle (File-Name sftlf) variieren von binären Daten (0 = kein Land, 1=
Land) bis zu ziemlich exakten %-Angaben. Die Land-Meer-Masken wurden so erstellt, dass sie
möglichst ähnliche Anteile als Meerfläche aussonderten und somit eine möglichst gute
Vergleichbarkeit zwischen den OAGCM-Datensätzen ermöglichen. Meist wurde eine Datenzelle als
Land klassiert, wenn sie einen Landanteil von mindestens 20% aufweist. Diese Land-Meer-Masken
unterscheiden nicht zwischen Meer- und Seeflächen. Datenpunkte über grossen Seen wurden als
Ozeanflächen klassiert. Um diese Lücken zu füllen wurden GIS-Daten der „Global Lakes and
Wetlands Database (GLWD)“ von Lehner und Döll (2004) beigezogen. Diese Daten geben die globale
Verteilung verschiedenster Typen von Wasserkörpern in einer Auflösung von wenigen Kilometern
wieder. Von den verschiedenen Wasserkörpern wurden Seen und Stauseen ausgewählt und Gitternetze
in der Auflösung der Klimamodelldaten darüber gelegt. Auf diese Weise konnte der Anteil an
Seeoberfläche an der Gesamtfläche jeder Gitterzelle berechnet werden (Abb. 11). Um die Lücken in
den Land-Meer-Masken aufzufüllen, wurden Gitterzellen mit einem grossen Seeanteil den
Landflächen zugeordnet. Die Daten der globalen Seenverteilung wurden auch benutzt, um die
Gleichgewichtstemperatur-Anomalie bei real existierenden und nicht nur potentiellen Seen
abzuschätzen. Dazu wurden die errechneten Gleichgewichtstemperatur-Anomalien jedes Datenpunktes
gemäss seines individuellen Seeanteils gewichtet.
b) MIROC
Seeflächenanteil
Seeflächenanteil
a) INMCM
Abb. 11. Seeflächenanteil pro Gitterzelle bei dem Modell mit der a) schlechtesten räumlichen Auflösung
(INMCM) und b) besten räumlichen Auflösung (MIROC).
34
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
2 Material und Methoden
2.6 Arbeitsschritte
Die von den AOGCMs verwendeten geographischen Projektionen der Welt sind nicht flächentreu. Für
die Berechnungen globaler Mittelwerte müssen die Datenpunkte gemäss ihrer Fläche gewichtet
werden,
da
sonst
Datenpunkte
mit
steigender
Breite
zunehmend
überproportional
im
Durchschnittswert vertreten wären. Diese Gewichtung erfolgt durch eine Kosinus-Funktion (Abb. 12).
Die Flächengewichtung wird monatlich durchgeführt, da die relevanten Flächen (Teq > 0°C) in der Zeit
variieren und somit je nach Monat eine unterschiedliche Anzahl an Datenpunkten verfügbar ist.
Abb. 12. Flächengewichtungsfaktor als Funktion der geographischen Breite. Hier wird gezeigt, um welche
Grössenordnung die Fläche und somit die Gewichtung von Datenpunkten entlang der Breite im Vergleich zum
Äquator (Gewichtung 1) abnimmt.
35
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.1 Globale Mittelwerte
3 Resultate
Es wurde eine grosse Menge an Resultaten produziert. Die wichtigsten Resultate und Visualisierungen
werden in diesem Kapitel aufgeführt und erläutert. Die Resultate sind nach verschiedenen
Betrachtungsweisen gegliedert. Allerdings lassen sich diese Betrachtungsweisen nicht vollständig von
einander ablösen. Viele beobachtbare Phänomene lassen sich nur durch die Kombination
verschiedener Betrachtungen beurteilen und erklären. Eine solche Diskussion der Resultate folgt in
Kapitel 4.
Wenn von einer Anomalie oder einer Veränderung eines Parameters die Rede ist, bezieht sich das
immer auf die Differenz zwischen der zukünftigen Klimatologie (2070-2099) und der
Basisklimatologie (1961-1990). Es wird also untersucht, wie stark sich die Gleichgewichtstemperatur
in diesem Jahrhundert verändern wird. Diese Werte können unter bestimmten Vorbehalten (siehe
Kapitel 2.1.2) auf die Oberflächentemperaturen von Seen übertragen werden. Bei allen Berechnungen
und Analysen wurden nur jene Datenpunkte berücksichtigt, welche in die GleichgewichtstemperaturAnomalie einfliessen. Es entfallen demnach alle Datenpunkte, welche über Ozeanflächen liegen oder
die Gleichgewichtstemperatur von 0°C nicht überschreiten. Damit wird verhindert, dass räumlich und
zeitlich unterschiedliche Datensätze miteinander verglichen werden. Globale Mittelwerte sind immer
flächengewichtet, Mittelwerte über Seeflächen sind nach Fläche und Seeanteil gewichtet. Die
Benennung der AOGCMs zeigt jeweils an, von welchem Klimamodell die verwendeten KlimaParameter stammen. Um die Gleichgewichtstemperaturanomalien in verschiedenen Klimazonen zu
untersuchen, wurden Intervalle von 15° Breite gebildet. Dabei wurden jeweils die sich entsprechenden
Breitengrad-Intervalle der Nord- und Südhalbkugel mit einer zeitlichen Verschiebung von sechs
Monaten zusammengefasst.
3.1 Globale Mittelwerte
Um die globale Grössenordnung der Auswirkungen des Klimawandels auf Seen abzuschätzen, wurden
die jährlichen globalen Mittelwerte der Gleichgewichtstemperatur-Anomalien berechnet (Tab. 2). Die
Temperaturänderung liegt bei der gesamten Landfläche je nach Klimamodelldaten bei einer
Erwärmung von 1.88-3.68°C, über den Seeflächen bei 1.66-4.23°C. Diese grosse Spannbreite ist
hauptsächlich auf die Daten des MIROC-Modells zurückzuführen, welche zu rund 30% höheren
Temperaturanstiegen führen. Werden die Resultate von MIROC nicht berücksichtigt, liegt die
durchschnittliche Zunahme der Gleichgewichtstemperatur über der Landfläche bei ca. 2.1°C mit
maximalen Abweichungen von rund 0.2°C. Über den Seeflächen ist die Streuung etwas grösser. Der
36
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.1 Globale Mittelwerte
Temperaturanstieg fällt bei den meisten Modellen über den Seeflächen etwas höher aus als über den
gesamten Landmassen. Bei Verwendung von GISS-Modelldaten hingegen wird über Seen ein deutlich
geringerer Temperaturanstieg berechnet. Dies ist auf fehlerhafte Daten über dem kaspischen Meer
zurückzuführen (siehe Kapitel 4.5). Einige Gebiete mit grossem Seeanteil, vor allem die Region der
Great Lakes, sind von einem besonders starken Gleichgewichtstemperaturanstieg betroffen, was zu
diesen verstärkten Temperaturanomalien führt (siehe Abb. 14).
Tab. 2. Jährlich gemittelte globale Gleichgewichtstemperatur-Anomalie von Seen über der gesamten Land- und
Seefläche berechnet mit Klimadaten sechs verschiedener AOGCMs.
BCCR
CCCMA
CNRM
GISS
INMCM
MIROC
Arithmetisches Mittel
d Teq gesamte Landflächen (°C)
1.93
2.31
2.34
1.88
2.19
3.68
2.39
d Teq Seeflächen (C°)
2.05
2.39
2.34
1.66
2.29
4.23
2.49
In Abb. 13. wird die Streuung der Gleichgewichtstemperatur-Anomalie innerhalb der Datensätze
betrachtet. Die rote Linie ist dabei der Median und innerhalb der blauen Box (begrenzt durch das 25%
und 75% Quartil) liegen 50% der Datenwerte. Werte, die über- oder unterhalb der Whisker liegen,
werden als Ausreisser behandelt und nicht bewertet. Die Median-Werte unterscheiden sich meist eher
gering von den flächengewichteten Mittelwerten (Tab. 2). Bei Klimamodellen mit grober räumlicher
Auflösung ist eine schwächere Streuung der Datenwerte zu erwarten, da die grossen Flächen der
Datenpunkte als Tiefpassfilter wirken (siehe Kapitel 2.5.3). Das MIROC-Modell mit der besten
räumlichen Auflösung zeigt denn auch deutlich die grösste Streuung. Das BCCR-Modell mit einer
durchschnittlichen räumlichen Auflösung zeigt zwar einige Ausreisser, eine grosse Menge an
Datenpunkten bewegt sich aber sehr nahe an 2C°. Die anderen Modelle zeigen trotz unterschiedlicher
Auflösungen kaum Unterschiede in der Streuung der Datenpunkte. Wie starke die Streuung ausfällt
scheint demnach nicht nur an der Auflösung der Modelldaten, sondern auch an den Charakteristiken
der einzelnen AOGCMs zu liegen. Obwohl der Trend in Richtung einer starken Erwärmung geht,
zeigen die Resultate immer auch einige Datenpunkte mit Abnahmen der Gleichgewichtstemperatur.
Diese Datenpunkte liegen aber ausschliesslich im Bereich der Ausreisser.
37
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.2 Räumliche Betrachtung
Abb. 13. Boxplot aller jährlich gemittelten Datenpunkte der Gleichgewichtstemperatur-Anomalien. Die Boxplots
zeigen den Median, das 25% und 50% Quartil und die Ausreisser, welche unter- und überhalb des Whiskers
liegen. d Teq bezeichnet die Gleichgewichtstemperatur-Anomalie in °C.
3.2 Räumliche Betrachtung
Globale Mittelwerte zeigen die Tendenz der Gleichgewichtstemperaturentwicklung auf, verdecken
aber jede räumliche und zeitliche Variabilität. Klimamodelle mit denselben globalen Mittelwerten
können völlig unterschiedliche räumliche Gleichgewichtstemperaturanomalien aufweisen. Die
Veränderungen der Gleichgewichtstemperatur werden deshalb in Abb. 14. räumlich dargestellt. Die
räumlichen Muster der Erwärmung variieren stark zwischen den Modellen. Dennoch können
Grossregionen identifiziert werden, welche gemäss der Mehrzahl der Klimamodelle einen eindeutigen
Trend aufweisen. Von besonders starken Erwärmungen betroffen ist demnach der Osten
Nordamerikas, der Nordwesten Russlands und teilweise die Anden. Sehr polnahe Gebiete erfahren
hingegen nur eine geringe Erhöhung der Gleichgewichtstemperatur. Dies steht vermeintlich im
Widerspruch zur verbreiteten Erkenntnis, dass besonders Gebiete hoher Breiten eine ausserordentlich
starke Erwärmung erfahren (siehe Kapitel 4.3).
38
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.2 Räumliche Betrachtung
a) BCCR
b) CCCMA
c) CNRM
d) GISS
e) INMCM
f) MIROC
Abb. 14. Jährlich gemittelte Veränderung der Gleichgewichtstemperatur bei Verwendung von Klimadaten der
AOGCMs a) BCCR, b) CCCMA, c) CNRM, d) GISS, e) INMCM und f) MIROC.
Das Auftreten von unterschiedlichen Klimazonen ist hauptsächlich von der geographischen Breite
abhängig. Breitengrade sind ein guter Ausgangspunkt für die Prüfung des Einflusses eines veränderten
Klimas auf Regionen. Deshalb werden in dieser Arbeit die räumlichen Variabilitäten der
Gleichgewichtstemperaturanomalien grösstenteils entlang der geographischen Breite untersucht. Abb.
15. zeigt die jährlich gemittelten Gleichgewichtstemperaturanomalien entlang der geographischen
Breite. Der grundsätzliche Verlauf der Gleichgewichtstemperaturanomalie ist bei allen Modellen
39
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.2 Räumliche Betrachtung
ähnlich. In Breiten über 40° Süd und 50° Nord fällt die Temperaturanomalie um rund 1°C ab, während
die Werte zwischen diesen beiden Breitengraden grösstenteils relativ konstant verlaufen. Die meisten
Modelle zeigen zudem zwischen ca. 50° und 60° nördlicher Breite ein lokales oder absolutes
Maximum der Erwärmung, ebenso um 40° Süd. In der Antarktis erhöht sich die Erwärmung gegen den
Pol.
Abb. 15. Jährlich gemittelte Gleichgewichtstemperaturanomalien der Landflächen entlang der geographischen
Breite. Die Datenlücke bei 60° Süd sowie gegen 90°Nord ist mit der Absenz von Landmasse zu erklären.
In Tab. 3. wurden die jährlich gemittelten Gleichgewichtstemperaturanomalien in BreitengradIntervallen berechnet. Die Unterschiede zwischen den verschiedenen Modelldaten sind hier markant
grösser als bei globalen Mittelwerten (Tab. 2). Die Unterschiede der Temperaturwerte zwischen den
AOGCMs (MIROC ausgeschlossen) übersteigen innerhalb eines Breitengrad-Intervalls praktisch nie
1°C. Bei Breitengraden ab 60° zeigen die meisten Modelle einen markanten Rückgang der Erwärmung
und in polaren Gebieten (75°-90°) die geringste Erwärmung. Die Resultate der unterschiedlichen
GCMs streuen zwischen 15°-30° am wenigsten, zwischen 60°-75° am stärksten.
Tab. 3. Jährlich gemittelte Gleichgewichtstemperaturanomalien in Breitengrad-Intervallen von 15°. Daten der
Nord- und Südhalbkugel wurden unter gleichen astronomischen Bedingungen (also einer zeitlichen
Verschiebung von 6 Monaten) zusammengefasst.
0°-15°
2.07
BCCR
2.58
CCCMA
2.73
CNRM
2.22
GISS
1.97
INMCM
3.43
MIROC
Arithmetisches 2.50
Mittel
d Teq Landflächen nach Breitengrad-Intervallen
15°-30°
30°-45°
45°-60°
60°-75°
2.04
2.21
2.18
1.43
2.55
2.58
2.32
1.90
2.60
2.64
2.17
1.52
2.15
1.99
1.88
1.06
2.20
2.45
2.63
2.17
3.27
3.70
4.57
3.86
2.47
2.60
2.63
1.99
40
75°-90°
0.96
1.63
1.63
1.08
1.99
2.72
1.67
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.2 Räumliche Betrachtung
Die Streuung der Temperaturanomalien in den einzelnen Breitengrad-Intervallen weist bei allen
Klimamodellen ähnlich Charakteristiken auf (Abb. 16). In den Tropen ist die Erwärmung sehr
konstant, die 25%- und 75%-Quartile liegen bei allen verwendeten AOGCM-Daten innerhalb ein paar
weniger
Zehntelgraden.
Zwischen
45°
und
75°
Breite
hingegen
weisen
die
Gleichgewichtstemperaturanomalien eine grosse Variabilität auf mit bis zu rund 2.5°C zwischen 25%und 75%-Quartil. Die Variabilität nimmt meist mit steigender Breite kontinuierlich zu und erreicht ihr
Maximum bei 45°-60° oder 60°-75°. Die Unterschiede der Resultate zwischen den einzelnen Modellen
sind von 45°-75° am stärksten ausgeprägt. Zwischen diesen Breitengraden sind auch die Unterschiede
zwischen Median-Werten und Mittelwerten (Tab. 3) teilweise sehr gross.
41
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.2 Räumliche Betrachtung
a) BCCR
b) CCCMA
c) CNRM
d) GISS
e) INMCM
f) MIROC
Abb. 16. Boxplots der jährlich gemittelten Datenpunkte der Gleichgewichtstemperatur-Anomalien innerhalb
Intervallen von 15° Breite. Es wurden Klimadaten der Modelle a) BCCR, b) CCCMA, c) CNRM, d) GISS, e)
INMCM und f) MIROC verwendet. Zu beachten sind die unterschiedlichen Temperaturskalen.
42
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.3 Zeitliche Betrachtung
3.3 Zeitliche Betrachtung
In dieser Arbeit wird die Gleichgewichtstemperatur von offenen Wasserflächen berechnet. Die
verwendeten Formeln sind bei Eisbedeckung, Eisbildungs- und Schmelzprozessen nicht adäquat. Der
Ausschluss der Datenpunkte mit einer negativen Gleichgewichtstemperatur führt zu einer räumlichen
und zeitlichen Eingrenzung der Daten. Während gewisse Gebiete (z.B. Teile der Antarktis) ganz
wegfallen, fliessen von hohen Breiten nur Daten der Sommermonate in die Analysen mit ein. Abb. 17.
zeigt, in wie vielen Monaten pro Jahr in den einzelnen Gitterzellen eine Gleichgewichtstemperatur von
> 0°C erreicht wird. Diese zeitliche Komponente muss bei der Interpretation der Resultate stets
berücksichtigt werden. Je besser die Auflösung der Daten eines Klimamodells, desto besser werden
die räumlichen Eigenschaften des Klimas erfasst. Das milde Klima entlang von Westküsten z.B. ist bei
MIROC gut zu erkennen, währen dieser Effekt bei INMCM überwiegend ausgemittelt wird. Während
auf der Südhemisphäre die Gleichgewichtstemperatur kaum je den Gefrierpunkt unterschreitet, nimmt
die Anzahl der Monate mit positiver Gleichgewichtstemperatur auf der Nordhemisphäre gegen Norden
ab. Auch eine steigende Kontinentalität reduziert die Monate mit positiven Werten der
Gleichgewichtstemperatur.
b) MIROC
Monate mit Teq > 0°C
Monate mit Teq > 0°C
a) INMCM
Abb. 17. Anzahl Monate pro Jahr mit einer Gleichgewichtstemperatur > 0°C bei a) schlechter räumlicher
Auflösung (IMNCM) und b) guter räumlicher Auflösung (MIROC).
Neben der räumlichen Betrachtung der Gleichgewichtstemperaturanomalien ist auch die zeitliche
Betrachtung von grosser Bedeutung. Der jährliche Mittelwert verdeckt intraannuelle Anomalien. Z.B.
kann die zusätzliche Erwärmung im Sommer von grosser Bedeutung sein, wenn bei einem
Wasserkörper im Sommer bereits kritische Temperaturwerte erreicht werden. Eine zusätzliche, starke
Temperaturerhöhung könnte Folgen wie extremer Sauerstoffmangel, Algenblüte oder das Umkippen
des Gewässers haben. Klimatische Extremereignisse treten in bestimmten jahreszeitlichen Perioden
auf (z.B. sommerliche Hitzewellen). Oft haben für Ökosysteme solche Extremereignisse grössere
43
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.3 Zeitliche Betrachtung
Folgen als die Entwicklung der durchschnittlichen Wassertemperatur. Auch wenn klimatische
Extremereignisse meist von kurzer Dauer sind, kann die Entwicklung der monatlich gemittelten
Gleichgewichtstemperatur Hinweise auf problematische Zeitperioden geben. Deshalb wird die
Entwicklung der Gleichgewichtstemperatur im Verlauf eines Jahres innerhalb einzelner BreitengradIntervallen untersucht (Abb. 18). Dabei wird nur die Nordhemisphäre betrachtet. Gemäss allen
Klimamodellen liegen in äquatornahen Gebieten bis 30° Breite kaum jahreszeitliche Variabilitäten der
Gleichgewichtstemperaturanomalien vor. Mit steigender Breite erhöhen sich auch die intra-annuellen
Variabilitäten. In hohen Breiten sind starke zeitliche Unterschiede ersichtlich. Das Minimum der
Erwärmung
fällt
auf
die
Sommermonate
in
der
polnahen
Zone.
Dort
fällt
die
Gleichgewichtstemperaturanomalie im Frühsommer stark ab und steigt im Spätsommer stark an. Alle
Modelle zeigen eine stete Zunahme der zeitlichen Variabilität der Gleichgewichtstemperaturanomalie
mit steigender Breite sowie das sommerliche Minimum in Polnähe. Die grössten Unterschiede
zwischen den Modellen bei der zeitlichen Entwicklung sind bei 60°-75° (teilweise auch bei 45°-60°)
Breite auszumachen. Während vier Modelle in dieser Zone eine unterdurchschnittliche Erwärmung
aufzeigen, prognostizieren zwei AOGCMs eine überdurchschnittliche Erwärmung.
44
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.3 Zeitliche Betrachtung
a) BCCR
b) CCCMA
c) CNRM
d) GISS
e) INMCM
f) MIROC
Abb. 18. Zeitliche Entwicklung der Gleichgewichtstemperatur in Breitengrad-Intervallen der Nordhemisphäre
mit Klimamodelldaten von a) BBCR, b) CCCMA, c) CNRM, d) GISS, e) INMCM und f) MIROC.
45
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.4 Energieflüsse
3.4 Energieflüsse
Der Änderung der Gleichgewichtstemperatur einer Gewässeroberfläche gehen Anomalien der
Wärmeflüsse voraus. Die Gleichgewichtstemperatur bestimmt die negativen Energieflüsse über die
langwellige Ausstrahlung sowie teilweise über die turbulenten Wärmeflüsse. Abb. 19. zeigt die
absoluten Wärmeflüsse nach Breitengrad-Intervallen am Beispiel des CNRM-Modells. Der radiative
Energieaustausch ist um ein vielfaches höher als der turbulente. Die absoluten Energieflüsse
unterscheiden sich in ihren Verhältnissen zueinander zwischen verschiedenen AOGCMs kaum.
Innerhalb
der
einzelnen
Breitengrad-Intervallen
ist
der
Netto-Energieaustausch
zwischen
Seeoberfläche und Atmosphäre null, da ein Gleichgewichtszustand beschrieben wird. Die grösste
Energiezufuhr in den Wasserkörper erfolgt über die langwellige Einstrahlung. Diese nimmt mit
steigender Breite kontinuierlich ab. Die solare Einstrahlung erreicht ihr Minimum zwischen ca. 45°60° Breite und steigt dann gegen die Polregionen an. Zwischen 75°-90° Breite ist die Solarstrahlung
der dominante positive Energiefluss. Dieser Effekt ist auf die zeitliche Einschränkung der Daten in
hohen Breiten auf Sommermonate zurückzuführen (siehe Kapitel 3.3). Bei den negativen
Energieflüssen dominiert die langwellige Abstrahlung. Die turbulenten Wärmeflüsse können positiv
oder negativ sein, bewirken aber einen negative Netto-Energiefluss. Der latente Wärmefluss ist
besonders in tiefen Breiten wichtig und nimmt mit steigender Breite ab. Umgekehrt verhält es sich mit
dem konvektiven Wärmefluss, welcher erst in kalten Klimaregionen (ca. ab 60° Breite) zu grösseren
Energieflüssen führt.
Abb. 19. Absolute Energieflüsse unter Verwendung von Basisklimadaten des Modelles CNRM nach
Breitengrad-Intervallen. Die Summe aller Energieflüsse innerhalb eines Breitengrad-Intervalls entspricht 0, da
sie einen Gleichgewichtszustand beschreiben. Die totalen Energieflüsse und die Grössenverhältnisse der
einzelnen Wärmeflüsse sind bei allen AOGCMs sehr ähnlich.
46
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.4 Energieflüsse
Die wegen des Klimawandels bewirkten Veränderungen der Energieflüsse werden in Abb. 20.
dargestellt. Die positiven und
negativen Anomalien der Energieflüsse gleichen sich in jedem
Breitengrad-Intervall aufgrund der Gleichgewichtsannahme aus. Die stärkste Zunahme aller
Energieflüsse erfährt die langwellige Einstrahlung. Gegen die Pole schwächt sich diese Zunahme ab.
Die solare Einstrahlung verändert sich gemäss der Mehrzahl der Klimamodelle bis ca. 60° Breite
kaum. In hohen Breiten ist allerdings eine deutliche Abnahme festzustellen. Die langwellige
Abstrahlung nimmt verhältnismässig wenig zu. Der negative Wärmefluss der latenten Wärme
hingegen vergrössert sich besonders in tieferen Breiten überproportional. Die Anomalie des
konvektiven Wärmeflusses zeigt in allen Breitengrad-Regionen und bei allen AOGCMs eine
Energiezufuhr in den See. Der Netto-Energie Transfer von der Seeoberfläche in die Atmosphäre durch
konvektiven Wärmefluss schwächt sich somit ab. Generell verändern sich die turbulenten
Wärmeflüsse überproportional stark. Die Änderungen aller Energieflüsse liegen im ein- bis knapp
zweistelligen Prozentbereich.
47
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.4 Energieflüsse
a) BCCR
d
d
b) CCCMA
d) GISS
d
d
c) CNRM
f) MIROC
d
d
e) INMCM
Abb. 20. Jährlich gemittelte Energieflussanomalien in einzelnen Breitengrad-Intervallen bei Verwendung von
Klimadaten der Modelle a) BCCR, b) CCCMA, c) CNRM) d) GISS, e) INMCM und f) MIROC.
48
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.5 Einfluss einzelner Klimafaktoren
3.5 Einfluss einzelner Klimafaktoren
3.5.1 Gleichgewichtstemperatur bei einem variablen Klimafaktor
Der Einfluss einzelner Klimafaktoren auf die Veränderung der Gleichgewichtstemperatur soll genauer
untersucht werden. Dies kann auf verschiedene Weise erreicht werden. In dieser Arbeit wird der
Einfluss der Klimafaktoren vor allem anhand der Veränderungen von nur einem Klimafaktor sowie
mit Regressionen abgeschätzt.
Die Gleichgewichtstemperatur für die Basisklimatologie wurde mit den benötigten Klimadaten
berechnet. Die Gleichgewichtstemperatur des zukünftigen Klimas wurde hingegen nicht wie bis anhin
mit der zukünftigen Klimatologie berechnet. Es wurden nur die Daten eines Klimafaktors unter
zukünftigem
Klima
benutzt,
die
restlichen
Klimafaktoren
wurden
dem
Datensatz
der
Basisklimatologie entnommen. Die durch Subtraktion der beiden Gleichgewichtstemperaturen
berechneten Anomalien zeigen also die Auswirkungen von nur einem veränderten Klimafaktor. Dies
wurde mit Daten des Klimamodells CNRM durchgeführt. In Abb. 21. werden die berechneten
Gleichgewichtstemperatur-Anomalien räumlich dargestellt. Zudem wird die Einfachregression
zwischen der berechneten Anomalie der Gleichgewichtstemperatur und der Anomalie des veränderten
Klimafaktors gezeigt.
49
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.5 Einfluss einzelner Klimafaktoren
a 1)
a 2)
b 1)
b 2)
c 1)
c 2)
d 1)
d 2)
50
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.5 Einfluss einzelner Klimafaktoren
e 1)
e 2)
f 1)
f 2)
Abb. 21. Gleichgewichtstemperaturanomalien bei Verwendung der Basisklimatologie und nur einem
Klimafaktor unter zukünftigem Klima. Es wurden Klimadaten des CNRM-Modelles verwendet. Die
Abbildungen 1) zeigen jeweils den jährlichen Mittelwert in räumlicher Ansicht, 2) zeigen die Einfachregression
der Gleichgewichtstemperatur-Anomalien mit den Anomalien eines Klimafaktors. Der Nullpunkt der Anomalie
des Klimafaktors fällt jeweils auf jenen der Gleichgewichtstemperaturanomalie. y beschreibt die
Regressionsgerade. Die Resultate werden gezeigt für den veränderten Klimafaktor a) Luftdruck, b)
Lufttemperatur, c) Dampfdruck, d) Windgeschwindigkeit, e) Bewölkung und f) solare Einstrahlung.
Der Oberflächenluftdruck beeinflusst den latenten Wärmefluss über die Bowen-Konstante (Formel
11). Die Luftdruck-Anomalien bewegen sich um ein paar 100 Pa und damit im tausendstel-Bereich
des Atmosphärendrucks. Die dadurch verursachten Gleichgewichtstemperatur-Anomalien sind minim
(Abb. 21. a). An einzelnen Datenpunkten erreichen sie maximal 0.05°C. Im Vergleich mit der
Grössenordnung der durch andere Klimafaktoren verursachten Anomalien ist der Einfluss des
Dampfdruckes vernachlässigbar. In der Folge wird dieser Faktor nicht weiter untersucht.
Die Anomalie der Lufttemperatur führt zu einer markanten Erhöhung der Gleichgewichtstemperatur
(Abb. 21. b). Einige räumliche Muster der Gleichgewichtstemperatur-Anomalien gleichen jenen unter
Einbezug aller Parameter, insbesondere in mittleren und hohen Breiten. Im Streudiagramm befinden
sich die Datenpunkte mit kleiner Varianz entlang der Regressionsgeraden mit einer Steigung von 0.46.
51
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.5 Einfluss einzelner Klimafaktoren
Die Änderungen des Dampfdrucks führen ebenfalls zu ausgeprägten GleichgewichtstemperaturAnomalien (Abb. 21. c). Dampfdruck und Gleichgewichtstemperatur sind positiv korreliert.
Auffallend ist die grosse Streuung der Datenpunkte. Die Gleichgewichtstemperatur reagiert räumlich
und zeitlich variabel auf Änderungen des Dampfdrucks. Die Beschreibung mit linearer Regression ist
schwierig.
Windgeschwindigkeits- und Bewölkungsanomalien haben im jährlichen Mittel einen eher geringen
Einfluss auf die Gleichgewichtstemperatur (Abb. 21. d und e). Während bei der Windgeschwindigkeit
eine deutlich negativ korreliert entsteht, ist die Korrelation bei der Bewölkung schwach positiv. Bei
der Windgeschwindigkeit ist festzustellen, dass trotz der generell negativen Korrelation eine Erhöhung
der Windgeschwindigkeit auch einen Gleichgewichtstemperatur-Anstieg bewirken kann.
Die Anomalien der solaren Einstrahlung führen insbesondere in den hohen Breiten der
Nordhemisphäre zu einer deutlichen Abkühlung der Gleichgewichtstemperatur (Abb. 21. e).
Änderungen in der Bewölkung und der solaren Einstrahlung zeigen teilweise inverse Auswirkungen,
was auf die starke Korrelation dieser Klimafaktoren hindeutet.
3.5.2 Regressionen der Gleichgewichtstemperatur und der Klimafaktoren
Die Reaktion der Gleichgewichtstemperatur auf die veränderten Klimafaktoren wird mit multipler
linearer Regression bestimmt. Auf globaler Ebene liegen die Werte der Zusammenhänge aller Modelle
in derselben Grössenordnung (Tab. 4). Die einheitlichsten Resultate werden bei der Lufttemperatur
erzielt. Die Gleichgewichtstemperatur steigt auf globaler Ebene pro °C höherer Lufttemperatur um
rund 0.55°C (0.48-0.63°C). Bei dem Dampfdruck sind die Unterschiede zwischen den Modellen
bedeutend grösser (0.09 -0.19°C pro Pa Dampfdruck). 1m-s stärkere Windgeschwindigkeit führt zu
einer
Abkühlung
von
0.69-1.24°C,
1%
Bewölkungszunahme
bewirkt
eine
-2
Gleichgewichtstemperaturanstieg von 0.016- 0.040°C und 1 Wm stärkere solare Einstrahlung eine
Temperaturzunahme von 0.020- 0.036°C. In globaler Grössenordnung liegen die primären
Ungenauigkeiten der ermittelten Einflüsse der Klimafaktoren in der teilweisen Nichtlinearität der
Zusammenhänge aufgrund starker geographischer Unterschiede.
52
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.5 Einfluss einzelner Klimafaktoren
Tab. 4. Reaktion der Gleichgewichtstemperatur auf die Veränderung einer Klimafaktor-Einheit.
BCCR
CCCMA
CNRM
GISS
INMCM
MIROC
Arithmetisches
Mittel
d Teq pro
d Tair (°C/°C)
0.613
0.511
0.520
0.476
0.567
0.632
0.553
d Teq pro d eA
(°C/Pa)
0.150
0.092
0.136
0.193
0.140
0.148
0.143
d Teq pro d u
(°C/ms-1)
-0.688
-0.885
-0.844
-1.243
-0.860
-1.033
-0.926
d Teq pro d C
(°C/%)
0.023
0.036
0.032
0.016
0.040
0.033
0.030
d Teq d HS
(°C/Wm-2)
0.026
0.033
0.030
0.028
0.020
0.036
0.029
In Tab. 5. wurde die Abhängigkeit der Gleichgewichtstemperatur von Anomalien der Klimafaktoren
innerhalb von Breitengrad-Intervallen berechnet. Die Daten der unterschiedlichen Klimamodelle
streuen stärker als bei globaler Grössenordnung. Alle Klimamodelle zeigen mit steigenden
Breitengraden einen Trend zu stärkerer Sensibilität der Gleichgewichtstemperatur auf LufttemperaturSchwankungen. Der Einfluss des Dampfdruckes scheint in sehr hohen Breiten am stärksten zu sein.
Die Windgeschwindigkeit ist besonders in tiefen Breiten wie auch in Polnähe wichtig. Die
Abhängigkeit der Gleichgewichtstemperatur von der Bewölkung ist zwischen 60° und 75° Breite am
höchsten, bei der solaren Einstrahlung zwischen 60° und 90°. Generell steigt der Einfluss der
Klimafaktoren auf die Gleichgewichtstemperatur mit zunehmender Breite.
Das grösste Problem bei der Regressionsanalyse auf regionaler Skala sind die teilweise sehr starken
Korrelationen zwischen den Klimafaktoren. Z.B. wird bei MIROC zwischen 30° und 60° Breite ein
negativer Zusammenhang zwischen Gleichgewichtstemperatur- und Bewölkungsanomalie errechnet.
Aufgrund der verwendeten Wärmeflussformeln ist allerdings nur ein positiver Zusammenhang
möglich. In diesen Breitengraden sind Bewölkung und solare Einstrahlung besonders stark korreliert,
was die Ursache dieses Fehlers ist. Die Resultate von Tab. 5. sind also kritisch zu betrachten,
besonders bei Klimafaktoren mit eher geringem Einfluss auf die Gleichgewichtstemperatur (siehe
Abb. 21).
Tab. 5. Einfluss einzelner Klimafaktoren auf die Gleichgewichtstemperatur in einzelnen Breitengrad-Intervallen.
d Teq pro d Tair (°C/°C)
BCCR
CCCMA
CNRM
GISS
INMCM
MIROC
Arithmetisches
Mittel
0°-15°
0.518
0.397
0.425
0.550
0.509
0.391
15°-30°
0.481
0.439
0.424
0.457
0.531
0.451
30°-45°
0.541
0.533
0.460
0.401
0.451
0.440
45°-60°
0.613
0.864
0.539
0.527
0.638
0.647
60°-75°
0.735
0.806
0.815
0.621
0.733
0.689
75°-90°
0.784
0.588
0.710
0.680
0.665
0.616
0.465
0.464
0.471
0.638
0.7332
0.6738
53
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.5 Einfluss einzelner Klimafaktoren
d Teq pro d eA (°C/Pa)
BCCR
CCCMA
CNRM
GISS
INMCM
MIROC
Arithmetisches
Mittel
0°-15°
0.216
0.138
0.123
0.186
0.212
0.154
15°-30°
0.162
0.144
0.126
0.145
0.140
0.160
30°-45°
0.202
0.033
0.172
0.265
0.251
0.164
45°-60°
0.296
-0.085
0.262
0.349
0.182
0.001
60°-75°
0.227
0.203
0.231
0.405
0.329
0.232
75°-90°
0.242
0.573
0.474
0.566
0.578
0.649
0.172
0.146
0.181
0.168
0.2712
0.514
dTeq pro d u (°C/ms-1)
BCCR
CCCMA
CNRM
GISS
INMCM
MIROC
Arithmetisches
Mittel
0°-15°
-0.772
-0.975
-1.331
-1.221
-1.054
-1.094
15°-30°
-0.897
-1.056
-0.881
-1.278
-0.992
-1.284
30°-45°
-0.754
-0.857
-1.050
-1.257
-0.894
-1.086
45°-60°
-0.236
-0.522
-0.514
-1.140
-0.466
-0.491
60°-75°
-0.766
-0.548
-0.708
-0.887
-0.747
-0.935
75°-90°
-1.001
-0.837
-0.951
-1.184
-1.058
-1.216
-1.075
-1.065
-0.983
-0.562
-0.765
-1.041
d Teq pro d C (°C/%)
BCCR
CCCMA
CNRM
GISS
INMCM
MIROC
Arithmetisches
Mittel
0°-15°
0.027
0.030
0.036
0.023
0.035
0.024
15°-30°
0.025
0.028
0.026
0.030
0.028
0.036
30°-45°
0.010
0.040
0.026
0.001
0.031
-0.019
45°-60°
0.028
0.078
0.032
0.005
0.052
-0.018
60°-75°
0.041
0.034
0.050
0.031
0.072
0.035
75°-90°
0.017
0.039
0.028
0.024
0.009
0.024
0.029
0.029
0.015
0.030
0.044
0.024
d Teq pro d HS (°C/Wm-2)
0°-15°
0.028
0.031
0.029
0.018
0.022
0.031
BCCR
CCCMA
CNRM
GISS
INMCM
MIROC
Arithmetisches
0.027
Mittel
15°-30°
0.026
0.028
0.025
0.027
0.015
0.029
30°-45°
0.022
0.032
0.026
0.028
0.012
0.016
45°-60°
0.027
0.056
0.025
0.022
0.019
0.034
60°-75°
0.049
0.052
0.053
0.045
0.047
0.043
75°-90°
0.051
0.062
0.049
0.047
0.043
0.047
0.025
0.023
0.031
0.048
0.050
54
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
3 Resultate
3.6 Einfluss unterschiedlicher Wärmeflussformeln
3.6 Einfluss unterschiedlicher Wärmeflussformeln
Um die Abhängigkeit der Resultate von den gewählten Wärmeflussformeln zu untersuchen, wurde die
Gleichgewichtstemperatur mit teilweise ausgetauschten Formeln berechnet. Bei der einen Berechnung
wurde eine alternative Formel für die atmosphärische Emissivität verwendet, Formel 5 wurde durch
Formel 6 ersetzt. Für die zweite Berechnung wurde eine alternative Formel für den latenten
Wärmefluss eingesetzt, Formel 8 wurde durch Formel 9 ersetzt. Die Unterschiede zwischen Standardund alternativer Formel werden in Kapitel 2.2.1.2 und 2.2.1.3 besprochen. Die Berechnungen wurden
mit CNRM-Klimadaten durchgeführt. Die atmosphärische Emissivität ist ein wichtiger Teil der
Berechnung der langwelligen Einstrahlung. Ein Wechsel der Formel für atmosphärische Emissivität
verändert also die Wärmeflussformel der langwelligen Einstrahlung. Mit Einsatz der alternativen
Formel für die langwellige Einstrahlung (Formel 6 von Idso and Jackson) wurde eine
Gleichgewichtstemperatur-Anomalie über der Landoberfläche von 2.10 °C errechnet. Dieser Wert
liegt um 0.24°C tiefer als bei Berechnung mit den Standardformeln. Über Seeflächen liegt die
ermittelte Gleichgewichtstemperatur-Anomalie mit einer Erwärmung von 2.06°C um 0.28°C tiefer als
bei Verwendung der Standardformeln. Bei Verwendung der alternativen Formel für den latenten
Wärmefluss (Formel 9 nach Meyer) erhöht sich die Gleichgewichtstemperatur über Land um 2.24°C
und über Seeflächen um 2.28°C. Dies entspricht einer 0.10°C resp. 0.06°C schwächeren Erwärmung
als bei Gebrauch der Standardformeln.
Die Unterschiede der absoluten Gleichgewichtstemperatur sind bei Verwendung verschiedener
Formeln hingegen markant (Abb. 22). Die alternative Formel für langwellige Einstrahlung führt in den
Tropen zu deutlich tieferen (ca. -2°C) und in Polargebieten zu höheren (ca. +2°C) Temperaturen.
Auch über Gebirgen (Himalaya, Rocky Mountains, Anden) wird eine deutlich höhere
Gleichgewichtstemperatur errechnet.
Die Verwendung der alternativen Formel für den latenten Wärmefluss bewirkt massiv tiefere
Temperaturen über ariden Gebieten (Nordafrika, Arabische Halbinsel bis Zentralasien). Generell liegt
die Gleichgewichtstemperatur rund 1.5°C tiefer als bei Einsatz der Standardformeln. Nur an den Polen
wird die Temperatur um ca. 0.5°C höher berechnet. Die Unterschiede fallen so aus, wie das anhand
der in Abb. 5 und 6 dargestellten Zusammenhänge zu erwarten war.
55
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
b)
Teq_Standard - Teq_Meyer
Teq _Standard - Teq_Idso_and_Jackson
a)
3 Resultate
3.6 Einfluss unterschiedlicher Wärmeflussformeln
Abb. 22. Differenz der jährlich gemittelten Gleichgewichtstemperaturen von alternativen Wärmeflussformeln
und Standardformeln unter CNRM-Basisklimatologie. Es wurden alternative Formeln für a) die atmosphärische
Emissivität (Idso and Jackson) und b) den latenten Wärmefluss (Meyer) verwendet. Zu beachten ist sind die
unterschiedlichen Temperaturskalen.
Die Differenzen zwischen Gleichgewichtstemperatur-Anomalien bei Verwendung von Standard- und
Alternativformeln fallen im Gegensatz zu den absoluten Werten gering aus (Abb. 23). Die
Unterschiede bewegen sich im Bereich von ein paar wenigen Zehntelgrad. Diese Abweichungen sind
zu gering, als dass sie das grundsätzliche räumliche Muster der Gleichgewichtstemperatur-Anomalien
der Standardformeln verändern könnten. Auch die Streuung der Datenpunkte und die zeitliche
Entwicklung der Änderungen unterscheiden sich kaum durch den Austausch einer Wärmeflussformel.
Lokal kann die Verwendung verschiedener Formeln gewisse Unterschiede bewirken (z.B. Himalaya,
Arabien und Zentralasien, Nordwestamerika). Bei grossskaliger Betrachtung sind diese Unterschiede
allerdings von geringer Bedeutung. Die absoluten Werte reagieren demnach viel sensitiver auf
unterschiedliche Gleichungen als die Temperaturdifferenzen.
56
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
a)
3 Resultate
3.6 Einfluss unterschiedlicher Wärmeflussformeln
dTeq _Standard - dTeq_Meyer
dTeq _Standard - dTeq_Idso_and_Jackson
b)
Abb. 23. Differenz der jährlich gemittelten Gleichgewichtstemperatur-Anomalien bei Verwendung der
Standardformeln und alternativer Formel für a) die atmosphärische Emissivität (Idso and Jackson) sowie b) den
latenten Wärmefluss (Meyer). Zu beachten sind die unterschiedlichen Temperaturskalen.
Die Entwicklung der Gleichgewichtstemperaturanomalien entlang der geographischen Breite
unterscheidet sich kaum durch Gebrauch verschiedener Formeln der Wärmeflüsse (Abb. 24). Die
Hauptunterschiede liegen in relativ konstanten Differenzen von 1-2 Zehntelgrad. Besonders über
Tropen und Subtropen verlaufen die Kurven nahezu identisch zueinander. Einige breitenabhängige
Unterschiede treten ab 50° Nord und 40° Süd auf.
Abb. 24. Gleichgewichtstemperatur-Anomalien berechnet mit Standard- und Alternativformeln entlang der
geographischen Breite. Die alternative Formel der langwelligen Einstrahlung (HA) basiert auf der Formel von
Idso and Jackson (Formel 6), jene für den alternativen latenten Wärmefluss (HV) auf der Formel von Meyer
(Formel 9). Die Datenlücke um 60° Süd ist auf die Absenz von Landmasse zurückzuführen.
57
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
4 Diskussion
4.1 Eignung des verwendeten Ansatzes
4 Diskussion
4.1 Eignung des verwendeten Ansatzes
Um die Auswirkungen des Klimawandels auf die Wassertemperatur von Seen abzuschätzen, ist die
Verwendung der Gleichgewichtstemperatur empfehlenswert. Dieser Ansatz ermöglicht die beste
Annäherung an die realen Energieflüsse zwischen Wasser und Atmosphäre und ist deshalb als
zuverlässiger zu betrachten als andere Ansätze. Die Gleichgewichtstemperatur ist nicht geographisch
gebunden wie beispielsweise empirische Ansätze und kann deshalb global eingesetzt werden. Die
Gleichgewichtstemperatur kann in komplexere Untersuchungen einfliessen, z.B. als Input-Faktor in
ein Seen-Modell.
Falls sich die Emission von Treibhausgasen ungefähr so entwickelt, wie dies bei dem
Emissionsszenario SRES A1B angenommen wird, ist mit massiven klimabedingten Veränderungen in
Seen zu rechnen. Auch bei Verwendung von Klimadaten wenig klimasensitiver AOGCMs liegt die
Erhöhung der Gleichgewichtstemperatur innerhalb von 60° Nord und Süd kaum unter 2°C. Diverse
der in Kapitel 1.4 beschriebenen Auswirkungen würden bis Ende dieses Jahrhunderts eintreffen.
4.2 Einfluss der Grössenskalen
Klima spielt sich in verschiedenen Skalen ab. Mit AOGCMs kann nur das grossskalige
Hintergrundklima modelliert werden. Gemäss Christensen et al. (2007) sind Prozesse unter der
Auflösung von AOGCMs (typischerweise in der Grössenordnung von 200km) wichtig, können aber
von AOGCMs nicht repräsentiert werden. Hochauflösende Klimamodelle deuten darauf hin, dass in
stark von der Orographie beeinflussten Regionen grossskalige Klimaentwicklungen beträchtlich
verändert oder in einigen Fällen sogar umgekehrt werden können (Christensen et al., 2007). Für
Gebiete mit starkem Einfluss der lokalen Gegebenheiten (z.B. Bergregionen) ist die Aussagekraft der
Resultate einer grossskaligen Untersuchung demnach gering. Regionale Klimamodelle können in
solchen
Fällen
zu
deutlichen
Verbesserungen
führen.
Allerdings
sind
die
Fehler
bei
Klimamodellierung kleiner Skalen grösser als bei Modellierung grosser Skalen (Randall et al., 2007).
Dies ist auch bei der modellierten Gleichgewichtstemperatur ersichtlich. Je kleinskaliger die
untersuchten Gebiete sind, desto stärker unterscheiden sich die Resultate aufgrund der verwendeten
Klimadaten. Während globale Mittelwerte der Gleichgewichtstemperatur-Anomalie bei allen
Modellen vergleichbar ausfallen, gibt es bei den räumlichen Mustern (Abb. 14) markante
58
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
4 Diskussion
4.3 Einfluss der Jahreszeit
Unterschiede. Es ist demnach schwierig, für Grossregionen wie Kontinente die Entwicklung der
Gleichgewichtstemperatur zu prognostizieren. Eine Ausnahme bilden die Tropen. Dort wird unter
Anwendung aller AOGCM-Klimadaten eine sehr uniforme Erwärmung prognostiziert (Abb. 16),
welche sich zwischen den Klimamodellen nur gering unterscheidet. Die Prognosen für die Tropen
scheinen demnach besser möglich und viel robuster zu sein als für andere Klimaregionen. In mittleren
bis hohen Breiten (45°-75°) hingegen streuen die berechneten Gleichgewichtstemperatur-Anomalien
stark. In ein paar wenigen Gebieten höherer Breiten sind die Resultate zwischen den AOGCMs relativ
konsistent. Dort sind die Aussagen über die zukünftige Entwicklung mit geringerer Unsicherheit
verbunden. Regionen, welche besonders stark von einer Erhöhung der Gleichgewichtstemperatur
betroffen sind, zeigen vor allem zwei Merkmale. Es ist dies eine deutliche Erhöhung der
Lufttemperatur bei gleichzeitiger Zunahme des Dampfdruckes. Dieser Effekt deutet auf die
Wasserdampf-Rückkoppelung hin (siehe Kapitel 2.3.2). Ein solcher Rückkoppelungseffekt ist nur bei
genügend grosser Feuchtigkeitsverfügbarkeit möglich. In der von einer besonders starken Erhöhung
der Gleichgewichtstemperatur betroffenen Region in Nord-Ost-Amerika sind die Voraussetzungen
dafür gegeben. Während die Lufttemperatur dieser Region ansteigt, wird zudem ein Anstieg des
Niederschlages (Christensen et al., 2007) und somit ein Trend zu einem feuchteren Klima erwartet.
Das stark klimasensitive AOGCM MIROC zeigt diesen Effekt sehr ausgeprägt. Die stärksten
Gleichgewichtstemperatur-Anomalien werden auf der Nordhemisphäre ab ca. 40° Breite sowie in
Tropenregionen modelliert. Gemäss Christensen et al. (2007) erhöht eine Erwärmung die räumliche
Variabilität des Niederschlages, was zu einer Verminderung des Regens in den Subtropen und einer
Erhöhung in hohen Breiten und in Teilen der Tropen führt. Auch die etwas stärkere Erwärmung der
Gleichgewichtstemperatur (rund 0.1°C) über Seeflächen als über der gesamten Erdoberfläche kann mit
dem Effekt der Wasserdampf-Rückkoppelung erklärt werden. Grosse Seen versorgen die Atmosphäre
mit Wasserdampf. Regionen mit einer grossen Seendichte liegen überwiegend in feuchten Klimaten.
Die Wasserverfügbarkeit über Gitterzellen mit grossem Seeflächenanteil ist demnach höher als über
der gesamten Landoberfläche und erlaubt somit einen stärkeren Rückkoppelungseffekt.
4.3 Einfluss der Jahreszeit
In hohen Breiten (ca. ab 60°) ist eine geringe Zunahme der Gleichgewichtstemperatur festzustellen.
Die solare Einstrahlung in diesen Gebieten geht markant zurück. Dies ist hauptsächlich auf die
Bewölkungszunahme in dieser Zone zurückzuführen. Dies scheint der oft formulierten Erkenntnis zu
widersprechen, dass ganz besonders in hohen Breiten ein überdurchschnittlich starker Klimawandel zu
erwarten ist (z.B. Mueller et al., 2009; Christensen et al., 2007; Meehl et al., 2007). Die Erklärung für
dieses
Phänomen
liefert
die
zeitliche
Betrachtung.
59
In
hohen
Breiten
fallen
die
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
4 Diskussion
4.4 Änderungen der Energieflüsse
Gleichgewichtstemperaturen in Wintermonaten unter 0°C und werden deshalb nicht in den
Berechnungen berücksichtigt. Mit steigender Breite schränken sich die verfügbaren Daten demnach
immer mehr auf die Sommermonate ein (Abb. 17). Gemäss Christensen et al. (2007) ist die
Temperaturzunahme in 60°-90° Nord im Sommer massiv geringer als Winter. Dies spiegelt sich auch
in den Gleichgewichtstemperatur-Anomalien in Breiten von 75°-90° und teilweise auch 60°-75°
wieder (Abb. 18). Das Minimum der Erwärmung liegt jeweils im Juni oder Juli, vorher fällt die
Anomalie der Gleichgewichtstemperatur stark, danach erhöht sie sich sofort wieder. In sehr hohen
Breiten wird also nicht vor allem die Erhöhung der Wasseroberflächentemperatur zu grossen
Veränderungen in Seen führen, sondern vielmehr Veränderungen in der Kryosphäre und somit der
Dauer der Eisbedeckung. Diese hat grossen Einfluss auf die physikalischen und ökologischen
Verhältnisse im See. Z.B. erlaubt die Absenz einer Eisschicht die Winddurchmischung des Wassers
und kann damit zu einem Regimewechsel der Stratifikation führen. Die Wichtigkeit der
Gleichgewichtstemperatur ist in sehr hohen Breiten deshalb untergeordnet.
In den Tropen und Subtropen erhöht sich die Gleichgewichtstemperatur-Anomalie zeitlich sehr
uniform. Mit steigender Breite nimmt auch die zeitliche Variabilität der Änderung der
Gleichgewichtstemperatur zu.
4.4 Änderungen der Energieflüsse
Ein verändertes zukünftiges Klima bewirkt Änderungen des Energieaustausches zwischen
Seeoberfläche und Atmosphäre. Aufgrund des grösseren Gehaltes an atmosphärischen Treibhausgasen
steigt der Energiegehalt der Atmosphäre. Dieser Energiezuwachs führt zu einem grösseren
Energieumsatz zwischen Wasseroberfläche und Atmosphäre. Dies geschieht durch höheren
langwelligen Energie-Input in den Wasserkörper und verstärkten radiativen und evaporativen
Energieausstoss (Abb. 20). Eine Verstärkung des Energietransfers erfolgt, wenn sich ein Wärmefluss
in der Richtung des absoluten Wärmeflusses entwickelt (z.B. langwellige Einstrahlung), eine
Abschwächung erfolgt bei Entwicklung in entgegengesetzter Richtung (z.B. konvektiver Wärmefluss).
Der geringste Zuwachs des Energieumsatzes findet zwischen 60°-90° Breite statt. Dies ist auf den
gegen
hohe
Breiten abnehmenden
Zuwachs
langwelliger
Einstrahlung und
evaporativen
Energieverluste, besonders aber auf die Abnahme der solaren Einstrahlung und die Abschwächung des
Wärmeverlustes durch konvektiven Energiefluss zurückzuführen. Die turbulenten Wärmeflüsse,
insbesondere der latente Wärmefluss, erfahren eine im Vergleich zu ihren absoluten Grössen
überproportionale Veränderung. Entgegen der generellen Erhöhung der Energieflüsse nimmt der
konvektive Energieverlust bei allen AOGCMs in allen Regionen ab, am stärksten in hohen Breiten.
Der konvektive Wärmefluss ist hauptsächlich abhängig von der Differenz von Gleichgewichts- und
60
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
Lufttemperatur.
Gemäss
Schmid
et
al.
(2009)
4 Diskussion
4.5 Robustheit der Resultate
steigt
die
Gleichgewichtstemperatur
der
Wasseroberfläche weniger stark an als die Lufttemperatur. Diese Tatsache wurde auch in dieser Arbeit
bestätigt (Tab. 4 und 5). In einem zukünftigen Klima liegt die Lufttemperatur demnach näher bei der
Gleichgewichtstemperatur als im Basisklima. Dies zeigt die Schwächen der Versuche, die
Wassertemperatur von Seen empirisch durch die Lufttemperatur zu bestimmen. Auch wenn diese
Zusammenhänge heute stimmen mögen, können sie unter einem sich wandelnden Klima ihre
Gültigkeit verlieren.
Bei den turbulenten Energieflüssen steigt die Dominanz des evaporativen Wärmeverlustes. Somit wird
sich das Bowen-Verhältnis (= HC/HV) mit der Zeit verringern. Der Übergang zur verstärkten
Evaporation kann auch Auswirkungen auf die Massenbilanz eines Sees haben. Dies betrifft
insbesondere Seen mit einem grossen Oberflächen-Volumen-Verhältnis und langer Verweildauer des
Wassers. Allerdings kann sich unter zukünftigem Klima auch der Wasserzufluss in einen See ändern.
Für konkrete Aussagen zur Massenbilanz eines Sees müsste zusätzlich die Entwicklung des
Niederschlages im Einzugsgebiet untersucht werden.
4.5 Robustheit der Resultate
Die
mit
unterschiedlichen
AOGCM-
Klimadaten
modellierten
Anomalien
der
Gleichgewichtstemperatur unterliegen teilweise massiven Differenzen, besonders bei kleinskaligen
Untersuchungsregionen. Die Robustheit der Resultate nimmt demnach mit steigender räumlicher
Auflösung ab. Da die Gleichgewichtstemperatur vollständig aus den von AOGCMs generierten
Klimafaktoren errechnet wird, ist die Güte der Modellierung der Gleichgewichtstemperatur von der
Güte der AOGCM-Klimadaten abhängig. Fehler und Unsicherheiten in den Klimadaten werden auf
die Gleichgewichtstemperatur übertragen. Einzelne Datenpunkte der Klimamodelle zeigen sehr
unplausible Klimaentwicklungen auf. Z.B. zeigt das GISS-Modell über dem Kaspischen Meer, das als
grösster See der Welt gilt, einen extremen Rückgang der Luftfeuchtigkeit sowie einen starken Anstieg
der Lufttemperatur. Bei der Gleichgewichtstemperatur führt dies zu einer deutliche Abkühlung. Ein
teilweises Austrocknen des Kaspischen Meeres könnte derartige klimatische Veränderungen bewirken.
Allerdings sind diese Effekte auf den südlichen und tiefen Bereich des Kaspischen Meeres beschränkt,
wo ein solches Szenario ausgeschlossen werden kann. Die Ursache dieser Extremwerte konnte nicht
schlüssig ermittelt werden. In einem Fall wie diesem könnten einzelne Ausreisser grösseren Einfluss
haben auf die Resultate. So zeigt das GISS-Model über den Seeflächen im Gegensatz zu allen anderen
Modellen einen geringeren Temperaturanstieg als über der gesamten Landfläche. Auch andere
Modelle zeigen punktuell sehr unplausible Entwicklungen auf. Dies erhöht die Unsicherheit der
Resultate einzelner AOGCMs. Dem kann mit der Bildung eines Multi-Modell-Mittelwertes begegnet
61
Auswirkungen des Klimawandels auf die Gleichgewichts4 Diskussion
Oberflächentemperatur von Seen in globaler Betrachtung 4.6 Verhältnis Gleichgewichtstemperatur- Klimafaktor
werden. Damit können Fehler einzelner Modelle ausgemittelt und konstante Entwicklungs-Trends
ersichtlich gemacht werden. Auch wenn die Zahl von sechs AOGCMs etwas klein ist, ist das
arithmetische Mittel aller Resultate als robuster einzuschätzen als die Resultate der einzelnen
Klimamodelle.
Die Verwendung alternativer Formel für Wärmeflüsse hat einen signifikaten Einfluss auf die absolute
Gleichgewichtstemperatur und deren räumliche Verteilung (Abb. 22). Im Gegensatz zu den absoluten
Werten ist der Einfluss alternativer Formeln auf die Gleichgewichtstemperatur-Anomalie hingegen
gering (Abb. 23 und 23) und bringt keine grundsätzlich unterschiedlichen Resultate hervor. Je nach
Kombination von Energieflussformeln könnten die Resultate allerdings stärker beeinflusst werden.
Zudem ist zu erwarten, dass sich alternative Formeln bei verschiedenen AOGCM-Klimadaten
unterschiedlich stark auswirken.
Dennoch ist klar ersichtlich, dass Gleichgewichtstemperaturen viel sensitiver auf den Einsatz
unterschiedlicher AOGCM-Datensätze reagieren als auf die Verwendung unterschiedlicher
Wärmeflussformeln. Gleichgewichtstemperatur-Untersuchungen mit Klimadaten nur eines AOGCMs
sind wenig aussagekräftig. Es sollte immer mit von möglichst vielen AOGCMs generierten
Klimadaten gearbeitet werden. Den weniger gravierenden Unsicherheiten aufgrund verschiedener
Wärmeflussformeln kann mit einer sorgfältigen, dem Untersuchungszweck angepassten Auswahl des
Formelsatzes begegnet werden.
4.6 Verhältnis Gleichgewichtstemperatur- Klimafaktor
Die
Untersuchung
des
Einflusses
einzelner
Klimafaktoren
auf
die
Änderung
der
Gleichgewichtstemperatur ist aufgrund diverser und komplexer Zusammenhänge zwischen den
Klimaparametern wie auch der Zusammenhänge verschiedener Wärmeflüsse schwierig. Die
Zusammenhänge zwischen Gleichgewichtstemperatur- und Klimafaktor-Anomalie sind teilweise stark
räumlich und zeitlich variabel.
Auf globaler Ebene hat die Lufttemperatur deutlich den stärksten Einfluss auf Veränderungen der
Gleichgewichtstemperatur (Abb. 21). Die Datenpunkte lassen sich relativ gut mit einer linearen
Einfachregression beschreiben, wobei die Steigung gegen höhere Lufttemperaturen leicht abnimmt.
Auch die veränderte Luftfeuchtigkeit hat entscheidenden Einfluss auf die Gleichgewichtstemperatur,
wobei die Daten stark streuen. Die starken Steigungen werden in den hohen Breiten und die geringen
Steigungen in tiefen Breiten erreicht aufgrund des stärkeren Effektes auf die langwellige Absorption
bei tiefen Dampfdrücken (siehe Kapitel 2.3.2). Zudem führt ein höherer Dampfdruck zur Reduktion
des Dampfdruckdefizites, was eine geringere Evaporation bewirkt. Die anderen Faktoren haben
geringen oder nur lokal grösseren Einfluss. Die Änderung nur eines Klimafaktors, wie dies modelliert
62
Auswirkungen des Klimawandels auf die Gleichgewichts4 Diskussion
Oberflächentemperatur von Seen in globaler Betrachtung 4.6 Verhältnis Gleichgewichtstemperatur- Klimafaktor
wurde, wird in der Natur so nicht vorkommen. Veränderungen eines Klimafaktors haben
Auswirkungen auf andere Klimaparameter. Z.B. würde ein Anstieg der Lufttemperatur in den meisten
Fällen ein Anstieg des Dampfdrucks nach sich ziehen oder eine Zunahme der Bewölkung ein
Rückgang der solaren Einstrahlung. Die genaue Reaktion der anderen Klimafaktoren ist jedoch nicht
eindeutig abzuschätzen und kann sich sehr unterschiedliche verhalten. Während z.B. generell von
einer konstanten relativen Luftfeuchtigkeit bei einer Lufttemperaturerhöhung ausgegangen wird, wäre
das bei einer Erhöhung der Lufttemperatur aufgrund einer Entwicklung zu ariderem Klima und starker
Reduktion der Bodenfeuchte nicht gegeben. Die Modellierung mit einem variablen Klimafaktor gibt
eine gute erste Übersicht über die Stärke des Zusammenhangs und illustriert die in den
Wärmeflussformeln beschriebenen physikalischen Vorgänge.
Der Einfluss der Lufttemperatur auf die Gleichgewichtstemperatur steigt mit zunehmender Breite an
und erreicht sein Maximum gemäss den meisten Klimamodellen zwischen 60° und 75° Breite (Tab.
8). Der Anstieg der Gleichgewichtstemperatur ist stets kleiner als der Lufttemperaturanstieg. Dies
steht im Einklang mit der Analyse der Wärmeflüsse von Schmid et al. (2009). Gemäss Mohseni und
Stefan (2003) vergrössert sich bei erhöhter Lufttemperatur das Wasserdampfdefizit über der
Wasseroberfläche drastisch, was zu einer starken evaporativen Abkühlung führt und somit die
Beziehung zwischen Wasser- und Lufttemperatur abschwächt. Auch auf Veränderungen des
Dampfdruckes reagiert die Gleichgewichtstemperatur in hohen Breiten stärker als in tiefen. Dies kann
auf die starke Änderung der langwelligen Absorption bei Anomalien tiefer Dampfdrücke
zurückgeführt werden. In hohen Breiten korrelieren Lufttemperatur und Luftfeuchtigkeit stark, in
tiefen Breiten hingegen kaum. In hohen Breiten ist die relative Luftfeuchtigkeit nahe 100% und
Feuchtigkeit ist zur Genüge verfügbar. Die Luftfeuchtigkeit ist demnach temperaturlimitiert und kann
als abhängig von der Lufttemperatur betrachtet werden.
Die Gleichgewichtstemperatur reagiert in hohen Breiten (ca. ab 60°) generell sensitiver auf
Veränderung des Klimas als in tieferen Breiten. Nur Anomalien der Windgeschwindigkeit haben in
den Tropen und Subtropen stärkeren Einfluss auf die Gleichgewichtstemperatur als in hohen Breiten.
63
Auswirkungen des Klimawandels auf die Gleichgewichts5 Schlussfolgerungen und Ausblick
Oberflächentemperatur von Seen in globaler Betrachtung 4.6 Verhältnis Gleichgewichtstemperatur- Klimafaktor
5 Schlussfolgerungen und Ausblick
Der Ansatz Gleichgewichtstemperatur eignet sich für die Abschätzung der zukünftigen
Wassertemperatur-Anomalien. Da die Gleichgewichtstemperatur nur von meteorologischen Faktoren
abhängt, können grosse Skalen untersucht werden. Die berechneten GleichgewichtstemperaturAnomalien eignen sich am besten zur Modellierung der Temperaturentwicklungen in gut
durchmischten und seichten Seen mit geringer Wärmespeicherkapazität. In sehr tiefen und
unregelmässig durchmischten Seen sind grössere Differenzen zwischen Gleichgewichts- und
Wassertemperatur-Anomalie zu erwarten. Aufgrund der beschränkten räumlichen Auflösung der
AOGCMs können nur die Auswirkungen des Hintergrundklimas auf Seen modelliert werden.
Die Entwicklung der Gleichgewichtstemperatur im Verlauf dieses Jahrhunderts weist bedeutende
räumliche Unterschiede auf. Gleichgewichtstemperatur-Anomalien weisen in mittleren bis hohen
Breiten eine sehr grosse Variabilität und Unsicherheit auf. In den Tropen hingegen ist eine räumlich
und zeitlich uniforme Entwicklung der Gleichgewichtstemperatur zu erwarten. Die Resultate in den
Tropen sind ausserordentlich robust. Sehr tiefe Breiten eignen sich deshalb besonders gut für
grossskalige Modellierung der Entwicklung der Gleichgewichtstemperatur.
Die Abhängigkeit der Gleichgewichtstemperatur von der Lufttemperatur nimmt mit steigender Breite
zu. Die Erhöhung der Gleichgewichtstemperatur bleibt jedoch stets deutlich unter der Erhöhung der
Lufttemperatur.
In
Folge
des
Klimawandels
nähert
sich
die
Lufttemperatur
also
der
Gleichgewichtstemperatur an. Der konvektive Wärmeverlust von Seen an die Atmosphäre nimmt ab,
während der evaporative Wärmeverlust überproportional zunimmt. Unter einem zukünftigen Klima ist
mit einem verstärkten evaporativen Wasserverlust zu rechnen, was für Seen mit sehr geringem
Durchfluss von Bedeutung sein kann.
Die Resultate dieser Arbeit sind abhängig von der Güte der Klimamodelle. Eine grosse Unsicherheit
stellt auch die künftige Entwicklung der Treibhausgasemissionen dar. Die Resultate dieser Arbeit sind
demnach nicht als Prognose zu verstehen. Stattdessen zeigen sie die wahrscheinlichen Entwicklungen
der Oberflächentemperatur von Seen unter der Annahme des SRES A1B-Szenarios.
Um die Reaktionen von Seen auf ein verändertes Klima genauer zu untersuchen, könnten die hier
berechneten Gleichgewichtstemperatur-Anomalien als Inputfaktor für Seemodelle genutzt werden. Die
Wassertemperatur
an
der
Oberfläche
könnte
genauer
wiedergegeben
und
die
neuen
Stratifikationszustände im See ermittelt werden. Dafür wären aber seespezifische Parameter nötig. Um
die Integration solch spezifischer Daten zu umgehen und um die grossskalige Betrachtung nicht zu
verlassen, könnten Seemodelle verschiedener Seetypen mit idealisierten Parametern mit den
64
Auswirkungen des Klimawandels auf die Gleichgewichts5 Schlussfolgerungen und Ausblick
Oberflächentemperatur von Seen in globaler Betrachtung 4.6 Verhältnis Gleichgewichtstemperatur- Klimafaktor
Gleichgewichtstemperatur-Anomalien gekoppelt werden. Damit könnte die Reaktion von Seen auf
Änderungen des Klimas besser und ausführlicher wiedergegeben werden.
Bei zukünftigen Berechnungen der Gleichgewichtstemperatur sollte die Wahl des Formelsatzes der
Wärmeflüsse sorgfältig vorgenommen und der zu untersuchenden Region und Fragestellung angepasst
werden. Für zuverlässige Daten sollten Berechnungen mit einer möglichst grossen Anzahl an
Klimadaten verschiedener AOGCMs durchgeführt und gemittelt werden. Die Verwendung von
Klimadaten eines einzelnen Klimamodelles ergibt lokal offensichtliche Fehler. Aufgrund der starken
Abhängigkeit der Resultate von den verwendeten Klimamodelldaten können bei Verwendung von nur
einem AOGCMs keine schlüssigen Aussagen gemacht werden.
Besonders in stark von veränderten Gleichgewichtstemperaturen betroffenen Regionen sollten
vertiefte Studien über die Entwicklung der Oberflächentemperaturen von Seen durchgeführt werden,
z.B. in der Region der Great Lakes. Es sollten Massnahmen zur Minderung der Folgen des
Temperaturanstieges untersucht und eingeleitet werden.
Gewisse Rückkoppelungseffekte im Klimasystem, insbesondere die Wasserdampfrückkoppelung
scheint von grosser Bedeutung für die Entwicklung der Oberflächentemperatur von Wasserkörpern zu
sein. Genauere Untersuchungen zu solchen Prozessen und deren Einfluss auf Seen wären zu
begrüssen.
65
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
6 Quellen
6.1 Literatur
6 Quellen
6.1 Literatur
Adrian R., O’Reilly C. M., Zagarese H., Baines S. B., Hessen D O., Keller W., Livingstone D. M.,
Sommaruga R., Straile D., Van Donk E., Weyhenmeyer G. A. and Winder M. 2009. Lakes as
sentinels of climate change. Limnology and Oceanography 54, 2283-2297.
Antonopoulos V. Z. and Gianniou S. K. 2003. Simulation of water temperature and dissolved
oxygen distribution in Lake Vegoritis, Greece. Ecological Modelling 160, 39-53.
Arnott S. E., Keller B., Dillon P. J., Yan N., Paterson M. and Findlay D. 2003. Using temporal
coherence to determine the response to climate change in boreal shield lakes. Environmental
Monitoring and Assessment 88, 365-388.
Bleckner T., Adrian R., Livingstone D. M., Jennings E., Weyhemeyer G. A., George D. G.,
Jankowski T., Järvinen M., Aonghusa C. N., Nõges T., Straile D. and Teubner K. 2007. Largescale climate signature in lakes across Europe: a meta-analysis. Global Change Biology 13,
1314-1326.
Blenckner T., Omstedt A. and Rummukainen, M. 2002. A Swedish case study of contemporary and
possible future consequences of climate change on lake function. Aquatic Sciences 64, 171-184.
Bleckner T. 2005. A conceptual model of climate-related effects on lake ecosystems. Hydrobilogia
533, 1-14.
Bogan T., Mohseni O. and Stefan H. G. 2003. Stream temperature-equilibrium temperature
relationship. Water Resources Research 39, 1245–1257.
Brooks A. S. and Zastrow J. C. 2002. The potential influence of climate change on offshore primary
production in Lake Michigan. Journal of Great Lakes Research 28, 597-607.
Buck A. L. 1981. New equations for computing vapor pressure and enhancement factor. Journal of
Applied Meteorology 20, 1527-1532.
Canadian Centre for Climate Modelling and Analysis (homepage). http://www.cccma.bc.ec.gc.ca/
eng_index.shtml. Zugriff: 9. 2009.
Christensen J. H., Hewitson B., Busuioc A., Chen A., Gao X., Held I., Jones R., Kolli R. K., Kwon W.
-T., Laprise R., Magaña Rueda V., Mearns L., Menéndez C. G., Räisänen J., Rinke A., Sarr A. and
Whetton P. 2007. Regional Climate Projections. In: Climate Change 2007: The Physical Science
Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental
Panel on Climate Change [Solomon S., Qin D., Manning M., Chen Z., Marquis M., Averyt K. B.,
66
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
6 Quellen
6.1 Literatur
Tignor M. and Miller H. L. (eds.)]. Cambridge University Press, Cambridge, United Kingdom and
New York, NY, USA.
Cogley, J. G. 1979. The albedo of water as a function of latitude. Monthly Weather Review 107, 775–
781.
Croley II T. E. 1990. Laurentian Great-Lakes Double-Co2 Climate Change Hydrological Impacts.
Climatic Change 17, 27-47.
Dake J. M. K. 1972. Evaporative cooling of a body of water. Water Resources Research 8, 1087-1091.
dos Reis R. J. and Dias N. L. 1998. Multi-season lake evaporation: energy budget estimates and CRLE
model assessment with limited meteorological observations. Journal of Hydrology 208, 135-147.
Downing J. A., Prairie Y. T., Cole J. J., Duarte C. M., Tranvik L. J., Striegl R. G., McDowell W. H.,
Kortelainen P., Caraco N. F., Melack J. M. and Middelburg J. J. 2006. The global abundance and
size distribution of lakes, ponds, and impoundments. Limnology and Oceanography 51, 2388-2397.
Dröscher I., Patoine A., Finlay K. and Leavitt P. R. 2009. Climate control of the spring clear-water
phase through the transfer of energy and mass to lakes. Limnology and Oceanography 54, 24692480.
Edinger J. E., Duttweiler D. W. and Geyer J. C. 1968. The response of water temperatures to
meteorological conditions. Water Resources Research 4, 1137-1143.
Eggers K. A. and Tetzlaff G. 1978. A simple model for describing the heat balance of a shallow lake
with application to Lake Chad. Boundary Layer Meteorology 15, 205–214.
Fang X. and Stefan H. G. 1999. Projections of climate change effects on water temperature
characteristics of small lakes in the contiguous U.S. Climatic Change 42, 377-412.
Fang X. and Stefan H. G. 2009. Simulations of climate effects on water temperature, dissolved
oxygen, and ice and snow covers in lakes of the contiguous United States under past and future
climate scenarios. Limnology and Oceanography 54, 2359-2370.
Franceschini, G. A. 1968. The influence of clouds on solar radiation at sea. Deutsche
Hydrographische Zeitschrift 21, 162-168.
Gleckler P.J., Taylor K. E. and Doutriaux C. 2008. Performance metrics for climate models. Journal
of Geophysical Research 113, D06104, doi:10.1029/2007JD008972.
Gooseff M. N., Strzepek K. and Chapra S. C. 2005. Modeling the potential effects of climate change
on water temperature downstream of a shallow reservoir, Lower Madison River, MT. Climatic
Change 68, 331-353.
Henderson-Sellers B. 1986. Calculating the surface energy balance for lake and reservoir modeling: a
review. Reviews of Geophysics 24, 625-649.
IPCC Data Distribution Centre (homepage). http://www.ipcc-data.org/index.html. Zugriff: 9. und 10.
2009.
67
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
6 Quellen
6.1 Literatur
Krajewski W. F. 1982. A graphical technique for river water temperature predictions. Ecological
Modelling 17, 209-224.
Leavitt P. R., Fritz S. C., Anderson N. J., Baker P. A., Bleckner T., Bunting L., Catalan J., Conley D.
J., Hobbs W. O., Jeppesen E., Korhola A., McGowan S., Rühland K., Rusak J. A., Simpson G. L.,
Solovieva N. and Werne J. 2009. Paleolimnological evidence of the effects on lakes of energy and
mass transfer from climate and humans. Limnology and Oceanography 54, 2330-2348.
Lehner B. and Döll P. 2004. Development and validation of a global database of lakes, reservoirs and
wetlands. Journal of Hydrology 296, 1-22.
Li J., Scinocca J., Lazare M., McFarlane N., Von Salzen K., Solheimet L. 2006. Ocean surface albedo
and its impact on radiation balance in climate models. Journal of Climate 19, 6314–6333.
Livingstone D. M. and Imboden D. M. 1989. Annual heat balance and equilibrium temperature of
Lake Aegeri, Swizterland. Aquatic Sciences 51, 351-369.
MacIntyre S., Fram J. P., Kushner P. J., Bettez N. D., O’Brien W. J., Hobbie J. E. and Kling G. W.
2009. Climate-related variations in mixing dynamics in an Alaskan arctic lake. Limnology and
Oceanography 54, 2401-2417.
MacKay M. D., Neale P. J., Arp C. D., De Senerpont Domis L. N., Fang X., Gal G., Jöhnk K. D.,
Kirillin G., Lenters J. D., Litchman E., MacIntyre S., Marsh P., Melack J., Mooij W. M., Peeters F.,
Quesada A., Schladow S. G., Schmid M., Spence C. and Stokes S. L. 2009. Modeling lakes and
reservoirs in the climate system. Limnology and Oceanography 54, 2315-2329.
Meehl G. A., Stocker T. F., Collins W. D., Friedlingstein P., Gaye A. T., Gregory J. M., Kitoh A.,
Knutti R., Murphy J. M., Noda A., Raper S. C. B., Watterson I. G., Weaver A. J. and Zaho Z. C.
2007. Global climate projections. In: Climate Change 2007: The Physical Science Basis.
Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel
on Climate Change [Solomon S., Qin D., Manning M., Chen Z., Marquis M., Averyt K. B., Tignor
M. and Miller H. L. (eds.)]. Cambridge University Press, Cambridge, United Kingdom and New
York, NY, USA.
Mooij W. M., Hülsmann S., De Senerpont L. N., Nolet B. A., Bodelier P. L. E., Boers P. C. M.,
Miguel Dionisio Pires L., Gons, H. J., Ibelings B. W., Noordhuis R., Porielje R., Wolfstein K. and
Lammens E. H. R. R. 2005. The impact of climate change on lakes in the Netherlands: a review.
Aquatic Ecology 39, 381-400.
Mortsch L. D. and Quinn F. H. 1996. Climate change scenarios for Great Lakes Basin ecosystem
studies. Limnology and Oceanography 41, 903-911.
Mohseni O. and Stefan H. G. 1999. Stream temperature/air temperature relationship: a physical
interpretation. Journal of Hydrology 218, 128-141.
68
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
6 Quellen
6.1 Literatur
Mueller D. R., Van Hove P., Antoniades D., Jeffries M. O. and Vincent W. F. 2009. High Arctic lakes
as sentinel ecosystems: Cascading regime shifts in climate, ice cover, and mixing. Limnology and
Oceanography 54, 2371-2385.
Neumann, J. 1954. Insolation in relation to cloud amount. Monthly Weather Review 82, 317-319.
Nunez M., Davies J. A. and Robinson P. J. 1972. Surface albedo at a tower site in Lake Ontario.
Boundary-Layer Meteorology 3, 77-86.
O'reilly C. M., Alin S. R., Plisnier P.-D., Cohen A. S. and Mckee B. A. 2003. Climate change
decreases aquatic ecosystem productivity of Lake Tanganyika, Africa. Nature 424, 766-768.
Payne R. E. 1972. Albedo of the Sea Surface. Journal of the Atmospheric Science 29, 959-970.
Pham S. V. and Leavitt P. R. 2008. Spatial variability of climate and land-use effects on lakes of the
northern Great Plains. Limnology and Oceanography 53, 728-742.
Quayle W. C., Peck L. S., Peat H., Ellis-Evans J. C. and Harrigan P. R.. 2002. Extreme responses to
climate change in Antarctic lakes. Science 295, 645-645.
Randall D. A., Wood R. A., Bony S., Colman R., Fichefet T., Fyfe J., Kattsov V., Pitman A., Shukla
J., Srinivasan J., Stouffer R.J., Sumi A. and Taylor K. E. 2007. Cilmate Models and Their
Evaluation. In: Climate Change 2007: The Physical Science Basis. Contribution of Working Group
I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change [Solomon S.,
Qin D., Manning M., Chen Z., Marquis M., Averyt K. B., Tignor M. and Miller H. L. (eds.)].
Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
Riley M. J. and Stefan H. G. 1998. MINLAKE: A dynamic lake water quality simulation model.
Ecological Modelling 43, 155-182.
Schmid M., Little J. C. and Wüest A. 2009. Effect of a changing climate on the lake surface
temperature: a global perspective and effects on a sensitive lake. Not published.
Stefan H. G., Fang X. and Hondzo M. 1998. Simulated climate change effects on year-round water
temperatures in temperate zone lakes. Climatic Change 40, 547-576.
Tranvik L. J., Downing J. A., Cotner J. B., Loiselle S. A., Striegl R. G., Ballatore T. J., Dillon P.,
Finlay K., Fortino K., Knoll L. B., Kortelainen P. L., Kutser T., Larsen S., Laurion I., Leech D. M.,
McCallister S. L., McKnight D. M., Melack J. M., Overholt E., Porter J. A., Prairie Y., Renwick
W. H., Roland F., Sherman B. S., Schindler D. W., Sobek S., Tremblay A., Vanni M. J., Verschoor
A. M., von Wachenfeldt E. and Weyhenmeyer G. A. 2009. Lakes and reservoirs as regulators of
carbon cycling and climate. Limnology and Oceanography 54, 2298-2314.
Trumpickas J., Shuter B. J and Minns C. K. 2009. Forecasting impacts of climate change on Great
Lakes surface water temperatures. Journal of Great Lakes Research 35, 454-463.
Verburga P. and Hecky R. E. 2009. The physics of the warming of Lake Tanganyika by climate
change. Limnology and Oceanography 54, 2418-2430.
69
Auswirkungen des Klimawandels auf die GleichgewichtsOberflächentemperatur von Seen in globaler Betrachtung
6 Quellen
6.2 Abbildungen
Wagner C. and Adrian R. 2009. Cyanobacteria dominance: Quantifying the effects of climate change.
Limnology and Oceanography 54, 2460-2468.
WCRP CMIP3 multi-model database (homepage). https://esg.llnl.gov:8443/index.jsp. Zugriff: 9. und
10. 2009.
Whitehead P. G., Wilby R. L., Battarbee R. W., Kernan M. and Wade A. J. 2009. A review of the
potential impacts of climate change on surface water quality. Hydrological Sciences-Journal 54,
101-123.
Williamson C. E., Saros J. E., Vincent W. F. and Smol J. P. 2009. Lakes and reservoirs as sentinels,
integrators, and regulators of climate change. Limnology and Oceanography 54, 2273-2282.
6.2 Abbildungen
Titelbild:
Nasa, Visible Earth. SeaWiFS-Bild der Great Lakes.http://veimages.gsfc.nasa.gov/1151/
S1999227180330.png. Zugriff: 27.4.2010.
Abb. 3:
Eigene Darstellung nach Edinger J. E., Duttweiler D. W. and Geyer J. C. 1968. The
response of water temperatures to meteorological conditions. Water Resources
Research 4, 1137-1143.
Abb. 5:
Henderson-Sellers B. 1986. Calculating the surface energy balance for lake and reservoir
modeling: a review. Reviews of Geophysics 24, 625-649.
Abb. 6:
Henderson-Sellers B. 1986. Calculating the surface energy balance for lake and reservoir
modeling: a review. Reviews of Geophysics 24, 625-649.
Abb. 7:
Meehl G. A., Stocker T. F., Collins W. D., Friedlingstein P., Gaye A. T., Gregory J. M.,
Kitoh A., Knutti R., Murphy J. M., Noda A., Raper S. C. B., Watterson I. G., Weaver
A. J. and Zaho Z. C. 2007. Global climate projections. In: Climate Change 2007: The
Physical Science Basis. Contribution of Working Group I to the Fourth Assessment
Report of the Intergovernmental Panel on Climate Change [Solomon S., Qin D.,
Manning M., Chen Z., Marquis M., Averyt K. B., Tignor M. and Miller H. L. (eds.)].
Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
Abb. 9:
Meehl G. A., Stocker T. F., Collins W. D., Friedlingstein P., Gaye A. T., Gregory J. M.,
Kitoh A., Knutti R., Murphy J. M., Noda A., Raper S. C. B., Watterson I. G., Weaver
A. J. and Zaho Z. C. 2007. Global climate projections. In: Climate Change 2007: The
Physical Science Basis. Contribution of Working Group I to the Fourth Assessment
Report of the Intergovernmental Panel on Climate Change [Solomon S., Qin D.,
Manning M., Chen Z., Marquis M., Averyt K. B., Tignor M. and Miller H. L. (eds.)].
Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA.
70
Persönliche Erklärung: Ich erkläre hiermit, dass ich die vorliegende Arbeit selbstständig verfasst und
die den verwendeten Quellen wörtlich oder inhaltlich entnommenen Stellen als solche kenntlich
gemacht habe.
Grüt, 26. 4. 2010
Stefan Hunziker