Trennender Schnitt

6. Flüsse in Netzwerken
Berechnung maximaler Flüsse
Satz 6.4. Ersetzt man in Algorithmus 6.1 den Schritt 2 durch
2a. Wähle den Knoten
.
, der zuerst in
eingefügt wurde. Setze
dann berechnet der Markierungsalgorithmus für beliebige Kapazitätsfunktionen in
einen Maximalfluß.
Beispiel 6.2. Anwendung des Markierungsalgorithmus. Tafel ✎
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
173
6. Flüsse in Netzwerken
max-flow min-cut
Trennender Schnitt
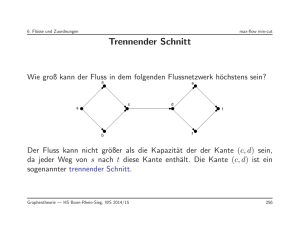
Wie groß kann der Fluß in dem folgenden Flußnetzwerk höchstens
sein?
a
e
c
d
s
t
f
b
! sein,
$% ist ein
Der Fluß kann nicht größer als die Kapazität der der Kante
da jeder Weg von nach diese Kante enthält. Die Kante
sogenannter trennender Schnitt.
"
#
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
174
Definition 6.5. Es sei & ( ')*+",#- ein Flußnetzwerk mit ' . 0/1 .
Für eine Teilmenge 243 heißt /65 7 98%;:< /= 8 2%: 2 Schnitt von ' .
Falls " 2%# 2 , so ist /65 ein trennender Schnitt.
Ein trennender Schnitt /65 mit minimaler Kapazität
>./65? 7 AC@ BED>F G0HI
6. Flüsse in Netzwerken
max-flow min-cut
heißt minimaler Schnitt.
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
6. Flüsse in Netzwerken
175
max-flow min-cut
& (')*JK",#-
Satz 6.5. [max-flow-min-cut-Theorem]
ist der Wert eines maximalen
In einem Flußnetzwerk
Flusses gleich der Kapazität eines minimalen Schnittes.
Beweis. Tafel ✎.
L
Bemerkung 6.2.
M
N
OPQNR > ./65R
M
Kennen wir einen Fluß und finden wir einen trennenden Schnitt
mit
, so ist ein Maximalfluß.
N
2
M
Für die Menge bei Terminierung von Algorithmus 6.1 ist
minimaler Schnitt (vgl. Beweis zu Satz 6.2).
/65
/65
ein
Der Markierungsalgorithmus berechnet also nicht nur einen maximalen Fluß sondern auch einen minimalen Schnitt.
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
176
6. Flüsse in Netzwerken
max-flow min-cut
Beispiel 6.3. Wie groß ist der Maximalfluß in dem folgenden Graphen?
N,S2%+T
[N,Z TUCVW YX N,S2%C/1 \N,./]_^`Y
X N,^a\VW Yb 4 f
N,./]\cP N,Scd(Ve also OPQNR . Die Kapazität des trennenden Schnittes 2gKTW+h^a\V
+_ScdCVW Also ist N ein Maximalfluß.
ist 8.
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
177
6. Flüsse in Netzwerken
Matchings
Matchings
Adam
Das Heiratsproblem lautet:
In einer Gruppe von Männer
und Frauen kennnen sich einige Männer und Frauen. Ist
es möglich, daß jeder mit einer seiner Bekannten verheiratet wird?
Eva
Hänsel
Kriemhild
Siegfried
Gretel
Tristan
Berta
Romeo
Julia
' .ij
H m2 8%0: n V 8 2%;: V
in zwei dis
2
klV ), so daß
heißt bipartit gdw.
Definition 6.6. Ein Graph
junkte Teilmengen und zerlegt werden kann (d.h.
für alle Kanten
gilt:
.
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
178
Definition 6.7. Es sei ' o pqj ein bipartiter Graph. Ein Menge r s
von
Kanten heißt Zuordnung (Matching) gdw. für alle H,tuH r mit
H,tP v H gilt: H,twxH y , d.h. die Kanten haben keinen gemeinsamen
Knoten.
6. Flüsse in Netzwerken
Matchings
Bemerkung 6.3.
M
M
Das Heiratsproblem ist genau dann lösbar, wenn ein Matching maximaler Mächtigkeit existiert.
M
Das wesentliche Problem besteht also darin, zu einem bipartiten Graphen ein Matching mit maximaler Mächtigkeit zu berechnen. Hierzu
können wir die das Problem als Flußproblem modellieren.
Alle Kanten des Orginalgraphen werden von
2
nach
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
M
Neuer Knoten
"
gerichtet.
179
; ",S8z für alle 8 2
M Neuer Knoten # und neue Kanten 98%#- für alle 8 V
M
6. Flüsse in Netzwerken
V
Matchings
und neue Kanten
Alle Kanten erhalten die Kapazität 1.
Beispiel 6.4. Transformiert man den bipartiten Graphen des gegebenen Heiratsproblem nach obigen Regeln ergibt sich:
S
s
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
T
t
180
M
6. Flüsse in Netzwerken
Matchings
N
Es sei ein Maximalfluß, der mit dem Markierungsalgorithmus berechnet wurde. Wegen der Ganzzahligkeit des Problems ist dann
auch ganzzahlig.
N
8 V kann dann nicht mehr als 1 hineinfließen.
M Aus einem Knoten 8 2 kann nicht mehr als 1 herausfließen.
M Daraus folgt, daß die Kanten zwischen 2 und V mit Fluß 1 ein MatM
In einen Knoten
ching bilden.
M
Die Anzahl dieser Kanten ist gleich dem Flußwert
M
Damit stellen diese Kanten ein Matching maximaler Mächtigkeit dar.
OlNR .
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
181
6. Flüsse in Netzwerken
Matchings
Beispiel 6.5. Für unser spezielles Heiratsproblem erhalten wir als eine
Lösung:
S
s
T
t
Es ist also nicht möglich, alle zu verheiraten. Tristan und Julia bleiben
bei dieser Lösung unverheiratet.
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
182
6. Flüsse in Netzwerken
Matchings
Das gewichtete Zuordnungsproblem
Das gewichtete Zuordnungsproblem lautet:
M
# V
M
Gegeben sei ein vollständiger bipartiter Graph, d.h. für alle
gibt es eine Kante, die und verbindet.
"
#
" 2
und
M
Auf den Kanten ist eine Gewichtsfunktion definiert.
M
Man finde ein Matching maximaler Mächtigkeit mit minimalem Gesamtgewicht.
Beispiel: Man verbindet im Heiratsproblem alle Männer mit allen
Frauen und drückt den Grad der Zuneigung durch ein Antipathiegewicht aus.
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
M
6. Flüsse in Netzwerken
183
Matchings
M
Es sind dann alle zu verheiraten und zwar so, daß die Gesamtantipathie möglichst klein und somit die Gesamtzuneigung möglichst groß
ist.
M
Zur Lösung von gewichteten Zuordnungsproblemen wendet man
ähnliche Verfahren wie bei der Berechnung von Maximalflüssen und
wie beim ungewichteten Zuordnungsproblem an.
Ein sehr bekanntes Verfahren ist der ungarische Algorithmus.
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
184
6. Flüsse in Netzwerken
Matchings
Zusammenfassung
M
M
Flußnetzwerk und Maximalfluß
Zunehmender Weg als Grundlage zur Berechnung von maximalen
Flüssen
Berechnung maximaler Flüsse mit dem Markierungsalgorithmus
M
max flow = min cut
M
M
Anwendung des Maximalflußproblems zur Berechnung maximaler
Matchings
Einführung in die Graphentheorie — FH Bonn-Rhein-Sieg, WS 01/02
185