Dienstag, 25.11.2014, 11:15 Uhr im HS 5 Aufgabe 1 (5 Punkte)

Dr.
Christian Werge, Steffen Hintze
WS 2014/2015
Grundwissen Schulmathematik
Übungsaufgaben Serie 5
Abgabe: Dienstag, 25.11.2014, 11:15 Uhr im HS 5
Aufgabe 1 (5 Punkte)
Von einem rechtwinkligen Dreieck ABC mit dem rechten Winkel bei C seien die Kathete a und der
entgegengesetzt gelegene Hypotenusenabschnitt q bekannt.
a) Berechnen Sie die Hypotenuse c und Kathete b.
b) Prüfen Sie Ihre Rechnungen durch Konstruktion mit q = 6 cm und a = 4 cm.
Aufgabe 2 (5 Punkte)
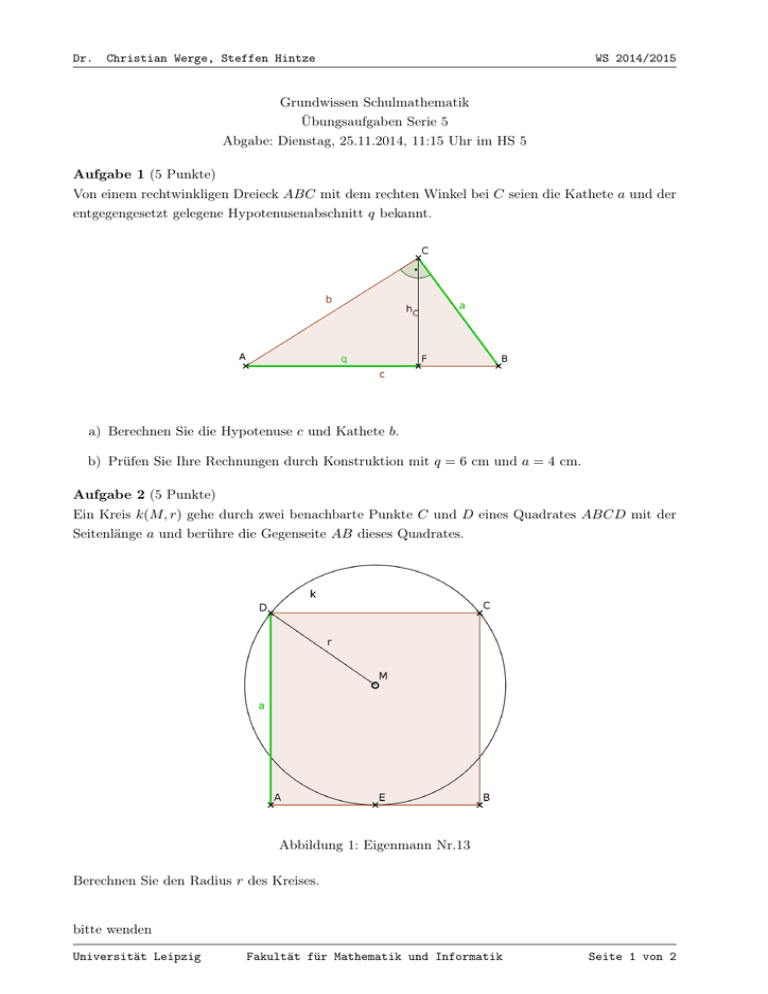
Ein Kreis k(M, r) gehe durch zwei benachbarte Punkte C und D eines Quadrates ABCD mit der
Seitenlänge a und berühre die Gegenseite AB dieses Quadrates.
Abbildung 1: Eigenmann Nr.13
Berechnen Sie den Radius r des Kreises.
bitte wenden
Universität Leipzig
Fakultät für Mathematik und Informatik
Seite 1 von 2
Dr.
Christian Werge, Steffen Hintze
WS 2014/2015
Aufgabe 3 (8 Punkte)
In der folgenden Aufgabe sollen Sie beweisen, dass es unendlich viele Primzahlen gibt, die bei
der Division durch 4 den Rest 3 haben. Mit anderen Worten: Zeigen Sie, dass es unendlich viele
Primzahlen p der Form p = 4k + 3 mit k ∈ N gibt. Zeigen Sie dafür zunächst die Wahrheit der
folgenden beiden Aussagen.
A1: Alle Primzahlen p ≥ 3 haben bei der Division durch 4 den Rest 1 oder den Rest 3.
A2: Gegeben seien zwei natürliche Zahlen a, b, die bei der Division durch 4 den Rest 1 haben.
Zeigen Sie, dass deren Produkt a · b bei der Division durch 4 den Rest 1 hat.
Nun soll der Beweis, dass es unendlich viele Primzahlen p der Form p = 4k + 3 mit k ∈ N gibt,
indirekt geführt werden. Es wird somit angenommen, dass es (nur) endlich viele Primzahlen p der
Form p = 4k + 3 mit k ∈ N gibt. Die Menge aller dieser Primzahlen sein
P = {p1 ; . . . ; pn }
und es wird die Zahl
q = 4 · p1 · . . . · pn − 1
betrachtet. Diese Zahl q hat eine bis auf die Reihenfolge der Faktoren eindeutige Primfaktorzerlegung
(siehe Hauptsatz der elementaren Zahlentheorie). Zeigen Sie, dass jede der folgenden Aussagen zu
einem Widerspruch führt.
A3: q ist durch 2 teilbar.
A4: In der Primfaktorzerlegung von q gibt es (mindestens) einen Primfaktor, der bei der Division
durch 4 den Rest 3 hat.
A5: Alle Primfaktoren von q haben bei der Division durch 4 den Rest 1.
Begründen Sie, warum damit der Beweis geführt wurde, dass es unendlich viele Primzahlen gibt,
die bei der Division durch 4 den Rest 3 haben.
Aufgabe 2 (2 Punkte)
Zeigen Sie, dass es beliebig große Intervalle von N gibt, in denen keine Primzahl liegt. Mit anderen
Worten: Zeigen Sie, dass es für jedes n ∈ N ein a ∈ N gibt, so dass alle Zahlen a; a + 1; . . . ; a + n − 1
zusammengesetzte Zahlen sind.
Universität Leipzig
Fakultät für Mathematik und Informatik
Seite 2 von 2