pdf - Digitale Schule Bayern

M 7.1
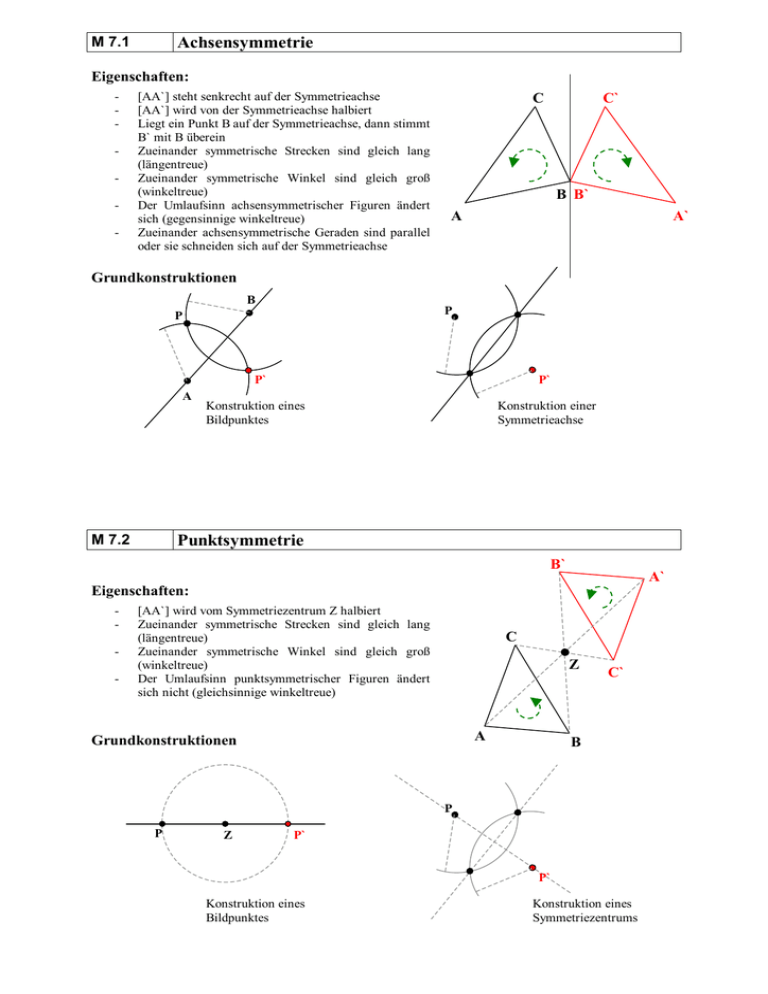
Achsensymmetrie
Eigenschaften:
-
[AA`] steht senkrecht auf der Symmetrieachse
[AA`] wird von der Symmetrieachse halbiert
Liegt ein Punkt B auf der Symmetrieachse, dann stimmt
B` mit B überein
Zueinander symmetrische Strecken sind gleich lang
(längentreue)
Zueinander symmetrische Winkel sind gleich groß
(winkeltreue)
Der Umlaufsinn achsensymmetrischer Figuren ändert
sich (gegensinnige winkeltreue)
Zueinander achsensymmetrische Geraden sind parallel
oder sie schneiden sich auf der Symmetrieachse
C`
C
B B`
A
A`
Grundkonstruktionen
B
P
P
P`
A
M 7.2
P`
Konstruktion eines
Bildpunktes
Konstruktion einer
Symmetrieachse
Punktsymmetrie
B`
A`
Eigenschaften:
-
[AA`] wird vom Symmetriezentrum Z halbiert
Zueinander symmetrische Strecken sind gleich lang
(längentreue)
Zueinander symmetrische Winkel sind gleich groß
(winkeltreue)
Der Umlaufsinn punktsymmetrischer Figuren ändert
sich nicht (gleichsinnige winkeltreue)
C
Z
A
Grundkonstruktionen
C`
B
P
P
Z
P`
P`
Konstruktion eines
Bildpunktes
Konstruktion eines
Symmetriezentrums
M 7.3
Grundkonstruktionen der ebenen Geometrie
Mittelsenkrechte zu [PP`]:
Konstruktionsüberlegung:
Zeichne:
P

PP` 

- k1  P; r1 >


2


- k 2 (P `; r2 = r1 )
P`
- Verbinde die Schnittpunkte von k1
und k2; es ergibt sich die gesuchte
Mittelsenkrechte.
Lotgerade von A auf g:
g
Konstruktionsüberlegung:
Zeichne:
- k1 A; r1 > d A; g
- k1 schneidet die Gerade in den
Punkten P und P`.
- Konstruiere die Mittelsenkrechte
der Srecke [PP`]
(
(
Konstruktion einer
Mittelsenkrechten
))
P
A
P`
Konstruktion eines Lotes
von A auf g
M 7.4
Grundkonstruktionen der ebenen Geometrie
Winkelhalbierende zu beliebigem ϕ:
Konstruktionsüberlegung:
Zeichne:
- k S ; r beliebig
- k schneide die Schenkel von ϕ in
den Punkten P und P`.
- Konstruiere die Mittelsenkrechte
der Srecke [PP`]
(
P
)
S
P`
Konstruktion einer
Winkelhalbierenden
Kreistangente an P ∈ k(M;r):
Konstruktionshilfe:
Zeichne:
- g mit M, P ∈ g
- Konstruiere in P das Lot auf g
P
M
Konstruktion einer
Kreistangente
M 7.5
Winkelbetrachtungen
Winkel an Geradenkreuzungen:
An einer Geradenkreuzung – siehe nebenstehende Skizze – nennt
man die gleichgefärbten Winkelpaare Scheitelwinkelpaare, die
verschieden gefärbten Winkelpaare Nebenwinkelpaare.
h
Es gilt:
-
Scheitelwinkel sind gleich groß
Nebenwinkel ergänzen sich zu 180°
g
h
Winkel an Parallelenpaaren:
g2
In nebenstehendem Bild
gleichgefärbte Winkelpaare
heißen Stufenwinkel.
β2
α2
γ2
δ2
g2
In nebenstehendem Bild
gleichgefärbte Winkelpaare
heißen Wechselwinkel.
Es gilt:
Es gilt:
Stufenwinkel sind gleich
groß!
Wechselwinkel sind gleich
groß!
β1
α1
γ1
δ1
g1
α2
β2
γ2
δ2
g1
β1
γ1
α1
δ1
g1 || g2
g1 || g2
h
M 7.6
Das Aufstellen von Termen / Termwerte
Zahlen, Variablen und deren sinnvolle
rechnerische Verknüpfungen nennt man auch
Terme.
Der Malpunkt zwischen Zahl und Variable kann
weggelassen werden (Malpunkte zwischen
Zahlen niemals!)
Anstelle der Variablen dürfen Zahlen aus der
sog. Definitionsmenge des Terms eingesetzt
werden.
Beachte: Tritt eine Variable mehrmals im Term auf, so muss
der gewählte Zahlenwert an jeder Position der Variablen
eingesetzt werden!
Durch Ausrechnen der entstehenden Aufgabe
erhält man den sog. Termwert.
Beispiele:
Zahlterme:
Variablenterme:
3, 5, 24, …
a, b, f, …
Vermischte Terme:
1 2
⋅ x −9⋅ y
3
Beispiel:
T (n ) =
1 2
⋅ n + 4 ⋅ n mit n ∈ IN
2
1
T (2 ) = ⋅ 2 2 + 4 ⋅ 2 = 2 + 8 = 10
2
Beispiel:
Terme können auch aus mehreren Variablen
zusammengesetzt sein. Zur Berechnung muss
man die jeder Variablen entsprechenden
Zahlenwerte einsetzen!
Sollen Termwerte für mehrere Zahlen berechnet
werden, sollte man eine Wertetabelle
verwenden!
T (x; y ) = x 2 − 2 ⋅ x ⋅ y mit x, y ∈ Q
2
1
5
1
1
 1
1
T  ; − 1 =   − 2 ⋅   ⋅ (− 1) = + 1 = = 1
4
4
4
2
 2
2
x
y
T(x;y) = x+y
1
2
3
2
3
5
3
4
7
4
5
9
M 7.7
Termumformungen / Summen und Differenzen
Beispiele:
Terme sind dann und nur dann gleichartig,
wenn sie – bis auf einen Zahlenfaktor – in allen
Variablen und den zu den einzelnen Variablen
eventuell gehörenden Hochzahlen (Exponenten)
übereinstimmen!
2 3 3 2
3
gleichartige Terme: 2 x y; x y;
yx
3
7
1 2 3 2
a b; ab ; ab 3 ; 9ab;
2
5
ungleichartige Terme:
Beispiele:
In Summen und Differenzen lassen sich nur
gleichartige Termteile zusammenfassen!
Sie werden addiert (subtrahiert), indem die
Zahlenfaktoren – unter Beibehaltung des
Variablenproduktes – addiert (subtrahiert)
werden (Distributivgesetz!).
Manchmal ist es sinnvoll, Summen oder
Differenzen
durch
Ausklammern
(Distributivgesetz!) in ein Produkt zu
verwandeln. Man nennt diesen Vorgang auch
Faktorisieren!
M 7.8
1 2
2
13
1 2
x d + x 2d =  + x 2d = x2 d
5
3
15
5 3
1
1
 1
a 2 c + ac − a 2 c = 1 −  a 2 c + ac = a 2 c + ac
2
2
 2
s 2 df 3 − sfk 2 = s 2 df 3 − sfk 2
Beispiele:
2 3
2 2
(
)
a b + a b − a 2b = a 2b ⋅ b 2 + b − 1
(
s 2 df 3 − sfk 2 = sf ⋅ sdf 2 − k 2
)
Termumformungen / Produkte
Beispiele:
Potenzen mit der gleichen Basisvariablen werden
multipliziert, indem man die gemeinsame
Basisvariable mit der Summe der Exponenten
potenziert.
x 3 ⋅ x 5 = x 3+ 5 = x 8
k 3 ⋅ k = k 3 ⋅ k 1 = k 3 +1 = k 4
allgemein :
an ⋅ am = an+m
(n, m ∈ IN )
Beispiele:
Produkte mit Variablen lassen sich vereinfachen,
indem man sowohl die Zahlenfaktoren als auch
die Potenzen mit gleichen Basisvariablen
zusammenfasst!
1 2 2 2
1 2
2
x d ⋅ x d = ⋅ ⋅ x 2 + 2 d 1+ 1 = x 4 d 2
5
3
5 3
15
1
1
a 2 c ⋅ abc ⋅ a 2 c = a 5bc 3
2
2
Manchmal ist es sinnvoll Produkte der Form
x2 ⋅ 2 ⋅ x − y
durch
Ausmultiplizieren
(Distributivgesetz!) in eine Summe oder eine
Differenz zu verwandeln.
Beispiele:
2
(
)
x ⋅ (2 x − y ) = x 2 ⋅ 2 x − x 2 ⋅ y = 2 ⋅ x 3 − x 2 ⋅ y
(
)
a 2b ⋅ b 2 + b − 1 = a 2b 3 + a 2b 2 − a 2b
M 7.9
Multiplikation (Summen und Differenzen) Klammerregeln
Werden zwei Klammern miteinander
multipliziert
(Ausmultiplizieren
von
Klammern / Distributivgesetz), so muss jedes
Glied der ersten Klammer – unter
Berücksichtigung der Vorzeichenregeln – mit
jedem Glied der zweiten Klammer
multipliziert
werden;
danach
wird
zusammengefasst (wenn möglich)!
Werden mehrere Klammern miteinander
multipliziert, so geht man Schritt für Schritt
vor: Zunächst werden zwei der Klammern
ausmultipliziert, das Ergebnis wird dann mit
der „nächsten“ Klammer multipliziert u.s.w..
Beispiel:
(2 ⋅ x + a) ⋅ (x − a + 3) =
= 2 ⋅ x2 − 2 ⋅ a ⋅ x + 6 ⋅ x + a ⋅ x − a2 + 3 ⋅ a =
= 2 ⋅ x 2 − a ⋅ x + 6 ⋅ x − a2 + 3 ⋅ a
Beispiel:
(x + 2) ⋅  3x − 1  ⋅ (x − 2) = [(x + 2) ⋅ (x − 2)] ⋅  3 x − 1  =
[
M 7.10
2
]
[

]
2
1
1


= x 2 + 2 ⋅ x − 2 ⋅ x − 4 ⋅  3 x −  = x 2 − 4 ⋅  3x −  =
2
2


1
= 3 ⋅ x 3 − ⋅ x 2 − 12 ⋅ x + 2
2
Beachte: Das Verwenden von Asoziativund
Kommutativgesetz
der
Multiplikation spart manchmal
viel Zeit!
Wichtig: Steht vor einer Klammer ein
Minuszeichen, so müssen alle
Glieder in der Klammer mit (-1)
multipliziert werden, d.h. es sind
alle Vorzeichen in der Klammer
zu ändern!

Beispiel:
− (3 ⋅ y − z − 2 ⋅ x ) = (− 1) ⋅ ((+ 3 ⋅ y ) + (− z ) + (− 2 ⋅ x )) =
= (− 1) ⋅ (+ 3 ⋅ y ) + (− 1) ⋅ (− z ) + (− 1) ⋅ (− 2 ⋅ x ) =
= −3 ⋅ y + z + 2 ⋅ x
Gleichungen / Allgemeines
Durch das Gleichsetzen von Termen entstehen
sog. Gleichungen. Eine Gleichung ist eine
mathematische Aussage, die wahr oder falsch
sein kann!
Die gesuchte(n) Größe(n) wird (werden) mit
(einer) Variablen (x, y, z, a, b, …) bezeichnet.
Anstelle der Variablen dürfen Zahlen aus der
sog. Grundmenge G der Gleichung (des Terms)
eingesetzt werden.
Durch sog. Äquivalenzumformungen kann
gezielt die Lösung (Lösungsmenge L) der
Gleichung bestimmt werden!
Eine Gleichung ist
- eindeutig
lösbar
über
der
Grundmenge, wenn sie genau eine
Lösung besitzt!
- allgemein
lösbar
über
der
Grundmenge, wenn alle Zahlen der
Grundmenge Lösungen sind!
- unlösbar, wenn sie keine Lösung in G
besitzt (Lösungsmenge ist dann die sog.
leere Menge L = { })!
Beispiele:
-
4⋅x – 5 = 3
2 - 3⋅x = 8
6 + 4⋅x = 3 – x
2⋅a – 4 = 5 + 5⋅a
Beispiele:
-
4⋅x – 5 = 3
4⋅1 – 5 = 3
4⋅2 – 5 = 3
4⋅3 – 5 = 3
Grundmenge: IN
Aussage ist falsch!
Aussage ist wahr!
Aussage ist falsch!
Beispiele:
- 4⋅x – 5 = 3
G = IN; L = {2} eindeutig
- 2⋅x + 2 = 2 + 2⋅x
G = Q; L = Q; allgemein
- x+1=x
G = Q; L = { }; unlösbar
- x+1=-2
G = IN; L = { }; unlösbar
M 7.11
Gleichungen / Äquivalenzumformungen
Eine Äquivalenzumformung ändert die
Lösungsmenge L einer Gleichung nicht. Ziel ist
es
eine
Gleichung
mit
Hilfe
von
Äquivalenzumformungen so zu vereinfachen,
dass deren Lösung(en) direkt abgelesen werden
kann!
Beispiel:
4⋅x +7 = 9
4 ⋅ x + 7 = 9 | −7
4 ⋅ x = 2 |: 4
1
x=
2
 1
L= 
2
Zunächst werden die Terme auf beiden
„Gleichungsseiten“
soweit
als
möglich
vereinfacht
(Klammern
auflösen;
zusammenfassen gleichartiger Glieder).
Danach …
… darf dieselbe Zahl (derselbe Term) auf
beiden
Gleichungsseiten
addiert
oder
subtrahiert werden!
Beispiel:
… darf auf beiden Gleichungsseiten mit
derselben, von Null verschiedenen Zahl
(demselben, von Null verschiedenen Term)
multipliziert oder durch dieselbe, von Null
verschiedene Zahl (denselben, von Null
verschiedenen Term) dividiert werden!
M 7.12
G = Q;
2−
2
1 

x − 3 − x 
3
3 

x − 3 | −x
−3
|: 2
3
x=−
2
L={}
1
⋅ (4 − 6 ⋅ x ) =
2
3⋅x =
2⋅x =
G = IN
Geometrie / Kongruente Figuren
Definition:
Deckungsgleiche
kongruent.
Figuren
nennt man
C
zueinander
C`
Wichtig:
Bei zueinander
kongruenten Figuren sind
zueinandergehörende Winkel und Strecken gleich groß.
Konstruktionsvorschriften, die kongruente Figuren
erzeugen heißen Kongruenzabbildungen!
B B`
A
A`
Die Achsenspiegelung und die Punktspiegelung gehören
zu den Kongruenzabbildungen, d.h. zueinander
achsensymmetrische oder punktsymmetrische Figuren
sind kongruent!
B`
C
Weitere wichtige Kongruenzabbildungen sind:
-
A`
Z
Drehungen
Verschiebungen
Mehrfachspiegelungen
A
B
C`
M 7.13
Geometrie / Kongruenzsätze für Dreiecke
Die Kongruenzsätze geben die Mindestbedingungen
an, wann die Form und die Größe eines Dreiecks
eindeutig festgelegt ist!
Dreiecke sind bereits dann kongruent …
…, wenn sie in allen drei Seitenlängen übereinstimmen
(Kongruenzsatz SSS).
…, wenn sie in zwei Seitenlängen und der
Winkelgröße
des
von
diesen
Seiten
eingeschlossenen
Winkels
übereinstimmen
(Kongruenzsatz SWS).
λ
…, wenn sie in einer Seitenlänge und zwei
Winkelgrößen zweier gleichliegender Winkel
übereinstimmen (Kongruenzsatz SWW oder
WSW).
…, wenn sie in zwei Seitenlängen und der
Winkelgröße des Winkels, welcher der größeren
Seite
gegenüberliegt,
übereinstimmen
(Kongruenzsatz SsW).
M 7.14
Geg.:
Ges.:
ϕ
ϕ
λ
µ
µ
δ
δ
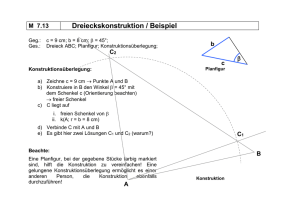
Geometrie / Dreieckskonstruktion / Beispiel
c = 9 cm; b = 8 cm; β = 45°;
Dreieck ABC; Planfigur; Konstruktionsüberlegung;
b
C2
c
Konstruktionsüberlegung:
β
Planfigur
a) Zeichne c = 9 cm → Punkte A und B
b) Konstruiere in B den Winkel β = 45° mit
dem Schenkel c (Orientierung beachten)
→ freier Schenkel
c) C liegt auf
i. freien Schenkel von β
ii. k(A; r = b = 8 cm)
d) Verbinde C mit A und B
e) Es gibt hier zwei Lösungen C1 und C2 (warum?)
C1
Beachte:
Eine Planfigur, bei der gegebene Stücke farbig markiert sind, hilft die Konstruktion zu vereinfachen! Eine
gelungene Konstruktionsüberlegung ermöglicht es einer anderen Person, die Konstruktion ebenfalls
durchzuführen
Konstruktion
A
B
M 7.15
Geometrie / Besondere Dreiecke
Definition:
Ein Dreieck mit zwei gleich langen Seiten heißt
gleichschenkliges Dreieck. Die gleich langen Seiten
nennt man Schenkel, die dritte Seite Basis. Der
Schnittpunkt der Schenkel heißt Spitze des Dreiecks;
die an der Basis anliegenden Innenwinkel werden
Basiswinkel genannt.
Spitze
Schenkel
Schenkel
Für jedes gleichschenklige Dreieck gilt:
a) Basiswinkel sind gleich groß
b) Achsensymmetrie zur Mittelsenkrechten der
Basis
Wichtig:
Basiswinkel
Definition:
Basiswinkel
Kathete
Ein Dreieck mit einem rechten Innenwinkel heißt
rechtwinkliges Dreieck. Die dem rechten Winkel
gegenüberliegende Seite nennt man Hypotenuse, die
beiden anderen Seiten bezeichnet man als Katheten.
Die Hypotenuse ist immer die längeste Seite des
rechtwinkligen Dreiecks.
M 7.16
Basis
Ein Dreieck mit drei gleich langen Seiten heißt
gleichseitiges Dreieck. In solchen Dreiecken sind
auch alle Winkel gleich groß (60°) →
Konstruktion eines 60° Winkels.
Kathete
Hypotenuse
Geometrie / Rechtwinkelige Dreiecke / Taleskreis
Vorbemerkung:
Jeder mathematische (Lehr-)Satz besteht aus
Voraussetzung (Wenn …) und Behauptung (…, dann
…).
C
Mathematische Sätze können wahr oder auch falsch
sein! Ihre Gültigkeit ist immer zu beweisen!
Vertauscht man Behauptung und Voraussetzung, so
erhält man den sog. Kehrsatz bzw. die Umkehrung des
Satzes.
A
B
Beispiel:
Satz:
Kehrsatz:
Wenn man zwei gerade Zahlen addiert,
dann ist der Summenwert wieder eine
gerade Zahl.
Wenn der der Summenwert bei der
Addition zweier Zahlen gerade ist, dann
wurden zwei gerade Zahlen addiert!
Bemerkung: Offensichtlich ist der Satz richtig (wie
kann man das beweisen?), der
Kehrsatz aber falsch (hier genügt ein
einziges Gegenbeispiel)!
Satz des Tales:
Wenn C auf einem Kreis mit dem Durchmesser
[AB] liegt, dann ist der Winkel ACB ein rechter
Winkel!
Es gilt auch die Umkehrung dieses Satzes:
Wenn der Winkel ACB ein rechter Winkel ist,
dann ist [AB] der Durchmesser des Kreises, auf
dem der Punkt C liegt!
Definition:
Der Umkreis eines rechtwinkligen Dreiecks
wird als Taleskreis bezeichnet!
M 7.17
Geometrie / Tangentenkonstruktion am Kreis
Geg.: Es sei A ∈ K(M; r);
Ges.: Tangente an K in A;
Konstruktionsüberlegung:
-
A
Zeichne die Halbgerade [MA[
Errichte in A die Lotgerade zu [MA[
M
S1
Geg.: Es sei A ∉ K(M; r); d(A; M) > r;
Ges.: Tangente von A an K;
Konstruktionsüberlegung:
-
Zeichne die Strecke [MA]
Der Taleskreis über [MA] schneidet
K in S1 und S2.
Verbinde A mit S1 und S2 → ges. Tangenten
M 7.18
A
M
S2
Geometrie / Tangentenkonstruktion am Kreis
Geg.: Es seien: K 1 (M1; r1 ); K 2 (M 2 ; r 2 ) (wie im Bild!)
Ges.: Tangentenpaar an K1 und K2;
L1
Konstruktionsüberlegung:
- Zeichne einen Kreis K 3 (M 2 ; r 3 = r 2 − r1 )
- Der Taleskreis über [M1M2] schneidet K3
in den Punkten S1 und S2.
- Verbinde M1 mit S1 und S2.
- Zeichne die Halbgeraden [M2S1[ und
[M2S2[.
- [M2S1[ schneidet K2 in L1.
- [M2S2[ schneidet K2 in L2.
- Errichte in L1 und L2 die Tangenten
an K2 → ges. Tangentenpaar
S1
M1
M2
r1
r2
S2
L2
M 7.19
Geometrie / Tangentenkonstruktion am Kreis
Geg.: Es seien: K 1 (M1; r1 ); K 2 (M 2 ; r2 ); M1M 2 > r1 + r 2 (wie im Bild!)
Ges.: Tangentenpaar an K1 und K2;
Konstruktionsüberlegung:
- Zeichne einen Kreis K 3 (M 2 ; r 3 = r 2 + r1 )
- Der Taleskreis über [M1M2] schneidet K3
in den Punkten S1 und S2.
- Verbinde M1 mit S1 und S2.
- Zeichne die Halbgeraden [M2S1[ und
[M2S2[.
- [M2S1[ schneidet K2 in L1.
- [M2S2[ schneidet K2 in L2.
- Errichte in L1 und L2 die Tangenten
an K2 → ges. Tangentenpaar
S1
L1
M2
M1
r1
L2
S2
r1
r2