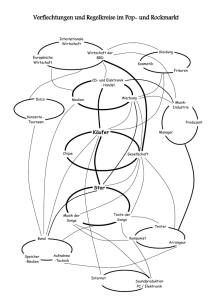
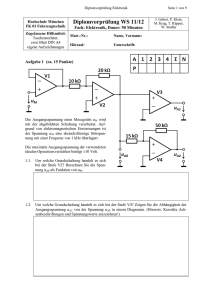
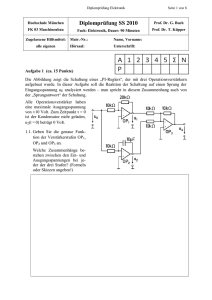
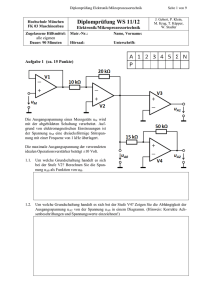
u - Hochschule Bremerhaven

Elektronik und Prozessmesstechnik
Hochschule Bremerhaven
I
Hochschule Bremerhaven --- IAE
I
Einleitung
Elektronik und Prozessmesstechnik
[ EPM ]
I.I
Umdruck zur Vorlesung
S Teil 1:
Signale und Systeme
S Teil 2:
Elektronische Bauelemente
Über die Homepage der Vorlesung <http://www1.hs---bremerhaven.de/kmueller/>
werden aktualisierte oder korrigierte Unterlagen im Verlauf der Vorlesung zur Verfügung
gestellt. Zu den Laborveranstaltungen müssen die entsprechenden Unterlagen in
gedruckter Form vorliegen.
S Teil 3:
Analoge Schaltungen
S Teil 4:
Digitalschaltungen
Unterlagen zur Lehrveranstaltung
Die jetzige Fassung 1.0a ist in vielen Details genauer gegenüber der Vorgängerversion.
I.II Elektronik und Prozessmesstechnik
Fast alle Geräte oder Anlagen enthalten Elektronik, die für wichtige Funktionen
verantwortlich ist. Dies gilt gleichermaßen für industrielle Anlagen und Prozesse als auch
für täglich benötigte Geräte im Haushalt. In Anbetracht der großen Bedeutung der
Elektronik ist es für Ingenieure unterschiedlicher Fachgebiete wichtig, die Grundlagen
elektronischer Schaltungen zu beherrschen. Diese Veranstaltung vermittelt die dazu
notwendigen Kenntnisse.
Revision:
V1.0a (major)
Datum:
September 2006
Prof. Dr.-Ing. Kai Müller
Hochschule Bremerhaven
Institut für Automatisierungs- und Elektrotechnik
An der Karlstadt 8
D---27568 Bremerhaven
Tel:
FAX:
+49 471 48 23 --- 415
+49 471 48 23 --- 418
E---Mail:
[email protected]
Obwohl die wirtschaftliche Bedeutung der Schlüsseltechnologie Elektronik offensichtlich
ist, hat die Elektronik-Industrie in Deutschland einen beispiellosen Niedergang erlebt.
Viele große Firmen wie AEG, Telefunken, Grundig und viele andere existieren nicht mehr
und sind lediglich Markennamen ausländischer Konzerne. Eine nennenswerte Fertigung
innovativer elektronischer Komponenten existiert kaum noch. Wir erleben gerade in
jüngster Zeit, dass deutsche Konzerne nicht in der Lage sind, beispielsweise ein
funktionsfähiges elektronisches Mauterfassungssystem zu entwicklen (Stand: September
2003). Oft hört man auch von “Elektronik-Problemen”. Elektronik arbeitet jedoch
verschleißfrei und besitzt prinzipiell eine unbegrenzte Lebensdauer. Die Probleme
entstehen nicht durch die Elektronik selbst, sondern durch Fehler im Entwurfs- oder
Fertigungsprozess der elektronischen Baugruppen.
Diese Worte mögen Motivation sein, sich mit dem wichtigen Fachgebiet Elektronik
auseinanderzusetzen. Die Veranstaltung umfasst neben dem unvermeidlichen theoretische
Teil auch den praktischen Umgang mit moderner Elektronik-CAD-Software (Multisim)
und die praktische Erprobung elektronische Schaltungen.
Elektronik und Prozessmesstechnik
II
Hochschule Bremerhaven --- IAE
Ich wünsche allen Hörern der Veranstaltung „Elektronik und Prozessmesstechnik” viel
Freude an dem faszinierenden und bedeutenden Fachgebiet.
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
II Inhalt
1
Bremerhaven, September 2006
III
Kai Müller
<kmueller@hs ---bremerhaven.de>
Tel: (0471) 4823 --- 415
2
3
4
Signale und Systeme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.1
Signalbeschreibung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1
1.2
Beispiele . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
Elektronische Netzwerke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.1
Digitalschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.2
Simulatoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.2.1
Digitale Simulatoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
Elementare Schaltungstechnik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
3.1
Analyse linearer Netzwerke . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
3.2
Quellenkonversion . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
Halbleiterbauelemente (aktive Bauelemente) . . . . . . . . . . . . . . . . . . . . . . . . . .
11
4.1
Eigenleitung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
4.2
Dotierung (Störleitung) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
4.2.1
n-Halbleiter (n-Dotierung) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
4.2.2
p-Halbleiter (p-Dotierung) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
Diode (pn-Übergang) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
4.3.1
17
4.3
5
6
7
Z-Diode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diodenschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
5.1
Dynamisches Verhalten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
5.2
Einweggleichrichterschaltung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
21
5.3
Brückengleichrichter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
22
Bipolartransistor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
24
6.1
Bestimmung des Arbeitspunktes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
27
6.2
PNP-Transistor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
28
Feldeffekttransistoren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
30
7.1
Sperrschicht-FET (JFET = Junction Field Effect Transistor) . . . . . . . .
31
7.2
p-Kanal-JFET . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
34
Elektronik und Prozessmesstechnik
8
9
IV
Hochschule Bremerhaven --- IAE
Elektronik und Prozessmesstechnik
V
Hochschule Bremerhaven --- IAE
MOSFETs (=Metal-Oxyde Semiconductor FET) . . . . . . . . . . . . . . . . . . . . . . .
34
8.1
CMOS (=Complementary MOS) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
36
16.1
Negierer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
Berechnung von Halbleiterschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
37
16.2
Addierer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
78
9.1
Elemente elektronischer Modelle . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
16.3
Subtrahierer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
79
9.2
Gesteuerte Quellen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38
16.4
Integrator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
83
9.3
Diode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
39
16.5
Differenzierer . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
85
9.4
Bipolartransistor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
40
16.6
Tiefpassfilter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
86
16.7
Hochpassfilter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
87
17 Beispiele für aktive Filter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
88
9.4.1
77
Übung: Berechnung des Kollektorstroms
mit Transistormodell . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
Übung: Verstärkungsunempfindliche Einstellung
des Kollektorstroms . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
41
17.1
Tiefpassfilter: Verstärkung 2, Grenzfrequenz 40Hz . . . . . . . . . . . . . . . .
88
JFET . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
42
17.2
Hochpassfilter: Verstärkung 0.8, Grenzfrequenz 5Hz . . . . . . . . . . . . . . .
90
9.5.1
Übung: Spannung und Strom in einem n-JFET . . . . . . . . . . . . .
43
17.3
Professionelles Tiefpassfilter für 1kHz . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
9.5.2
Verwendung eines JFET als Spannungsverstärker
(Wechselspannungen) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18 Messschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
44
9.4.2
9.5
16 Operationsverstärker-Schaltungstechnik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10 Transistorkenngrößen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18.1
Gleichrichterschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
44
18.1.1 Präzisions-Einweggleichrichter . . . . . . . . . . . . . . . . . . . . . . . . . . .
92
10.1
Großsignalverhalten . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
45
18.1.2 Präzisions-Zweiweggleichrichter . . . . . . . . . . . . . . . . . . . . . . . . .
93
10.2
Kleinsignalverhalten (Wechselstromverhalten) . . . . . . . . . . . . . . . . . . . .
45
19 Effektivwertmessung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
94
11 Transistorgrundschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
11.1
Kleinsignal-Ersatzschaltbilder . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
11.1.1 Bestimmung von differenziellen Widerständen . . . . . . . . . . . . .
49
11.1.2 Beispiel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
49
Emitterschaltung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
12 Kollektorschaltung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
11.2
12.1
19.1
Näherungsweise Effektivwertmessung über den Betragsmittelwert . . .
97
20 Scheitelwertmessung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
99
21 Analoge und digitale Systeme . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
101
22 Digitalschaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
102
22.1
Verwirklichung digitaler Funktionen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
102
22.2
Logische Signale und Funktionen (Gatter) . . . . . . . . . . . . . . . . . . . . . . .
103
22.3
Elementare Gatter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
104
22.3.1 Inverter (Negation) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
104
Kleinsignal-Ersatzschaltbild mit Transistor . . . . . . . . . . . . . . . . . . . . . . .
56
13 Differenzverstärker . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
59
14 Operationsverstärker . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
60
22.3.2 Konjunktion (AND) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
104
Prinzip von OP-Schaltungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
65
22.3.3 Disjunktion (OR) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
105
15 Komparator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
70
22.3.4 NAND . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
105
14.1
15.1
Schmitt-Trigger . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
72
22.3.5 NOR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
105
15.2
Fensterkomparator (Fensterdiskriminator) . . . . . . . . . . . . . . . . . . . . . . .
75
22.3.6 Antivalenz (exklusiv ODER, XOR) . . . . . . . . . . . . . . . . . . . . . . .
106
E K. Müller
Elektronik und Prozessmesstechnik
VI
Hochschule Bremerhaven --- IAE
22.3.7 Equivalenz (XNOR) . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
106
22.4
Vorrangregeln für boolsche Algebra . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
106
22.5
Funktionen für eine Variable (UNARY OPERATORS) . . . . . . . . . . . .
107
22.6
Funktionen für zwei Variablen (BINARY OPERATORS) . . . . . . . . . . .
108
22.7
Übung: Aufstellen einer Wahrheitstabelle . . . . . . . . . . . . . . . . . . . . . . . .
108
22.8
Rechenregeln für eine Variable und eine Konstante . . . . . . . . . . . . . . . .
109
22.9
Verwirklichung einfacher Gatterfunktionen durch
mechanische Schalter . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
110
23 Rechenregeln für mehrere Variablen (wichtig!) . . . . . . . . . . . . . . . . . . . . . . . . .
111
23.1
Kommutativgesetz (Vertauschen von Operanden) . . . . . . . . . . . . . . . . .
111
23.2
Assoziativgesetz (Zusammenfassen von Operanden) . . . . . . . . . . . . . . .
112
23.3
Distributivgesetz (Verteilen von Operanden) . . . . . . . . . . . . . . . . . . . . .
112
23.4
DeMorgansche Gesetze (Negationsregeln) . . . . . . . . . . . . . . . . . . . . . . .
112
23.5
Kürzungsregeln . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
112
24 Mehrstufige Logik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
113
25 Universelle Schaltungen mit NAND- oder NOR-Gattern . . . . . . . . . . . . . . . . .
113
25.1
Ungenutzte Eingänge . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
114
25.2
AND- und OR-Funktion mit NAND und NOR . . . . . . . . . . . . . . . . . . .
114
25.3
Verwirklichung von OR-Gattern mit NAND . . . . . . . . . . . . . . . . . . . . . .
115
25.4
Verwirklichung von AND-Gattern mit NOR . . . . . . . . . . . . . . . . . . . . . .
115
26 Normalformen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
115
27 Minimieren (Optimieren) von Digitalschaltungen . . . . . . . . . . . . . . . . . . . . . . .
118
27.1
KV-Diagramm für zwei Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
119
27.2
KV-Diagramm für drei Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
119
27.3
KV-Diagramm für vier Variablen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
120
28 Literatur . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
123
1
Elektronik und Prozessmesstechnik
1
Hochschule Bremerhaven --- IAE
Signale und Systeme
In der Elektronik --- wie auch in anderen Bereichen der Ingenieurwissenschaften --- hat sich
das Denken in Signalen und Systeme etabliert. Signale im allgemeinen beschreiben
Energien, Material, Informationen oder anderen Größen. Signale können also
verschiedener Natur sein. In der Elektronik verstehen wir unter Signalen i.a. die
Spannungen und Ströme einer Schaltung. Zusätzlich können auch elektrische und
magnetische Feldstärken, Induktion oder andere Signale in der Elektronik eine Rolle
spielen.
Ein dynamisches System stellt eine Funktionseinheit dar zur Verarbeitung und
Übertragung von Signalen, wobei die Systemeingangsgrößen als Ursache und die
Systemausgangsgrößen als deren zeitliche Auswirkung zueinander in Relation
gebracht werden.
In der Elektronik sind Systeme die elektronischen Bauelemente oder die aus
elektronischen Bauelementen gebildeten Netzwerke.
System
Eingangsspannung
elektronisches
Netzwerk
Ausgangsspannung
Signale
Bild 1.1:
Beispiel für ein System
Mit dieser Vorgehensweise lassen sich auch komplexe Schaltungen mit einem Höchstmaß
an Übersichtlichkeit entwerfen.
1.1
Signalbeschreibung
Signale bestehen immer aus einem Wert und einer Einheit. Beispielsweise kennzeichnet
u 1 = 40V
(1.1)
eine Spannung von 40 Volt. Große und kleine Werte werden durch einen entsprechenden
Zusatz zur Einheit beschrieben, z.B. 19μA (= 19 Mikroampere = 1,9 10 ---5A).
Man unterscheidet im wesentlichen drei verschiedene Signale:
S
Gleichsignale (DC). Diese Signale sind konstant, d.h. sie ändern sich nicht über der
Zeit.
E K. Müller
2
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Harmonische Signale (AC). Die Signale sind “sinusförmig”, d.h. sie sind periodische
Funktionen über der Zeit.
Zeiger werden durch unterstrichene Großbuchstaben gekennzeichnet.
S
Transiente, d.h. “einmalige” oder beliebige Funktionen der Zeit.
transiente Signale werden durch Kleinbuchstaben gekennzeichnet.
Praktisch vorkommende Signale können aus der Kombination dieser Signalformen
bestehen.
2.5
2
1.5
1
0.5
U1
DC
1
0.5
0
---0.5
U2
AC
3
u3(t)
transienter
Vorgang
2
1
0
6
u4(t) = u1(t)+u2(t)+u3(t)
4
u4(t)
2
0
0
20
40
60
80
100
120
Zeit [s]
Bild 1.2:
3
Hochschule Bremerhaven --- IAE
Der Augenblickswert
Gleichsignale werden durch Großbuchstaben gekennzeichnet.
S
E K. Müller
Elektronik und Prozessmesstechnik
Signaltypen und Überlagerung
In Bild 1.2 ist die Überlagerung der drei Signaltypen zu einem Signal u4(t) gezeigt.
Kleinbuchstaben kennzeichnen Augenblickswerte.
Harmonische Signale werden i.a. nicht durch den Augenblickswert, sondern durch
komplexe Zeiger beschrieben.
^
cos ωt + Ô 
u(t) = u
(1.2)
wird durch den komplexen Zeiger
^
U = u e jÔ
2
(1.3)
eindeutig beschrieben. Man kann sich den Zeiger mit der Winkelgeschwindigkeit ω in der
komplexen Ebene rotierend vorstellen. Der Augenblickswert folgt dann aus dem Realteil
dieses Ausdrucks
^
cos ωt + Ô  .
u(t) = Re2 U e jωt = 2 U cos ωt + Ô  = u
(1.4)
Der Faktor 2 gibt den Zusammenhang zwischen Scheitelwert und Effektivwert an, da ein
komplexer Zeiger per Definition die Länge des Effektivwerts besitzt.
Der Wert U ist der Betrag des Zeigers U und Ô sein Winkel in der komplexen Ebene.
Die Gleichung (1.4) hat auch eine einfache grafische Interpretation. Der zeitliche Verlauf
folgt aus der Projektion des mit τ = ωt umlaufenden Zeigers auf die reelle Achse.
E K. Müller
4
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
1.2
jIm
ωt
2 U
5
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Beispiele
Bei einem Ohmschen Widerstand gilt
Ô
(1.7)
U = RI .
Daraus folgt
Re
*
*
(1.8)
S = UI = RI I = RI 2 = P .
1.5
1
0.5
0
---0.5
---1
---1.5
Die Scheinleistung in einem Widerstand ist stets reell, also entsteht nur reine
Wirkleistung P.
0
Ein Spule mit der Induktivität L besitzt die komplexe Impedanz
(1.9)
Z L = jωL .
5
Man erhält für die Scheinleistung an einer Induktivität folglich
*
*
(1.10)
10
S = UI = Z L I I = jωLI 2 = jQ .
15
Die Scheinleistung ist rein imaginär. Damit tritt positive Blindleistung auf. Die Definition
einer positiven Blindleistung für Induktivitäten ist eine Konvention. Eine Induktivität
nimmt folglich keine Leistung auf, sondern tauscht nur Leistung mit der Spannungs- oder
Stromquelle aus.
Bei einem Kondensator erhalten wir für die komplexe Impedanz
20
Winkel ωt
j
.
ZC = 1 = −
jωC
ωC
25
Für die Scheinleistung gilt
*
*
S = U I = ZC I I = −
Bild 1.3:
(1.11)
Zusammenhang zwischen komplexem Zeiger und zeitlichem Verlauf der
Spannung
Mit Hilfe der komplexen Rechnung lassen sich sehr elegant Netzwerke berechnen, die mit
harmonischen Größen betrieben werden. Auch Leistungen (Wirk- und Blindleistungen)
folgen sehr kompakt aus den Zeigergrößen. Für die komplexe Leistung gilt
*
S = P + jQ = U I .
j 2
I = − jQ .
ωC
Die Scheinleistung ist rein imaginär. Damit tritt negative Blindleistung auf.
Aufgabe: Bestimmen Sie Wirk- und Blindleistung für folgende Last (f = 50Hz).
I
(1.5)
U = 230V
R = 12Ω
UR
UL
I* ist dabei der konjugiert komplexe Zeiger des Stromes
*
I = I e −jÔ .
(1.6)
Bild 1.4:
Ohmsch-induktive Belastung
L = 80mH
(1.12)
E K. Müller
6
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
Die gesamte Impedanz der Last ergibt sich zu
(1.13)
Damit folgt für die komplexe Scheinleistung
*
S=UI =U
 
U
Z ges
2
U2
= U* =
.
R − jωL
Z ges
(12Ω) 2 + (2 π 50 1s 80mH) 2
+j
U R = RI =
R
U,
R + jωL
U L = jωLI =
jωL
U.
R + jωL
U R = 42.7V − j 89.4V ,
(1.15)
U L = 187.3V + j 89.4V .
(1.21)
I = 3.56A − j 7.45A .
(230V)2 2 π 50 1s 80 mH
(12Ω) 2 + (2 π 50 1s 80mH) 2
Im
(1.16)
U
Den Verläufe von Spannung, Strom und Leistung zeigt Bild 1.5.
Re
400
200
0
---200
---400
Ôui
UR
20
10
0
---10
---20
i [A]
p [W]
3000
2000
1000
0
---1000
---2000
Bild 1.6:
2
0
5
10
15
20
25
ωt
Bild 1.5:
(1.20)
bzw.
= 818W + 1.714kVar .
u [V]
(1.19)
Mit Zahlenwerten erhält man
Mit den Zahlenwerten für R und L erhält man
S=
(1.18)
U = UR + UL ,
(1.14)
2
2
R + jωL
= 2 U R2 2 + j 2U ωL2 2 .
R +ω L
R +ω L
R 2 + ω 2L 2
(230V) 2 12 Ω
Hochschule Bremerhaven --- IAE
mit
Nach konjugiert komplexer Erweiterung erhält man
S = U2
7
Der Spannungsumlauf in der Masche in Bild 1.4 ergibt
Z ges = R + Z L = R + jωL .
*
Elektronik und Prozessmesstechnik
I
UL
Zeigerdiagramm bei ohmsch-induktiver Last
Elektronische Netzwerke
Netzwerke lassen sich mit den bekannten Methoden zur Berechnung passiver Netzwerke
(mit den passiven Bauteilen R, L und C) berechnen. Hinzu kommen zusätzlich aktive
Bauelemente (Transistoren, Triacs, Thyristoren, Röhren) sowie weitere Halbleiterbauelemente.
Verläufe von Spannung, Strom und Leistung bei ohmsch-induktiver Last
Die Zusammenhänge lassen sich auch gut im Zeigerdiagramm wiedergeben. Es gilt
I=
U
.
Z ges
(1.17)
Aktive Bauelemente enthalten (gesteuerte) Spannungs- und/oder Stromquellen.
Hierzu werden Modelle der einzelnen Transistortypen (z.B. BJT, JFET, MOSFET, IGBT)
benötigt. Man bezeichnet Schaltungen dieser Art als analoge Schaltungen.
E K. Müller
Elektronik und Prozessmesstechnik
2.1
8
Hochschule Bremerhaven --- IAE
Digitalschaltungen
Viele elektronische Schaltungen enthalten Digitaltechnik oder bestehen ausschließlich aus
digitalen Schaltungen. Diese Schaltungen werden nicht mit den bekannten Knoten- und
Maschengleichungen analysiert, sondern mit Hilfe boolscher Logik.
2.2
Simulatoren
Die Verwendung von Simulatoren ist ein Standard bei dem Entwurf und bei der Analyse
elektronischer Schaltungen. Eine komplexe Schaltung lässt sich nicht vollständig
berechnen. Insofern sind Simulatoren eine wertvolle Unterstützung für den Entwurfsprozess. Im Rahmen dieser Lehrveranstaltung werden wir die moderne Elektronik-CAD-Software Multisimt von Electronics Workbench einsetzen, die sowohl analoge als auch
digitale und gemischte Schaltungen beliebiger Komplexität simulieren kann.
Analoge Schaltungen erfordern die Lösung von algebraischen Gleichungssystemen und die
Integration eines Systems nichtlinearer Differenzialgleichungen. Eine der populärsten
Simulationsprogramme ist SPICE von der University of Berkeley (1975).
Der Name “Spice” steht für Simulation Program for Integrated Circuits Emphasis. Damit
kommt zum Ausdruck, dass sich mit Spice nicht nur einfache Schaltungen, sondern auch
komplexe integrierte Schaltungen mit Hilfe sogenannter Subcircuits simulieren lassen.
Dieses Konzept ermöglicht eine hierarchische Struktur, die eine übersichtliche Darstellung
auch größerer Schaltungen gestattet. Subcircuits dürfen wieder Subcircuits enthalten.
Die Hersteller leistungselektronischer Bauteile wie IGBTs oder MOSFETs stellen oft
Modelle in Form von Subcircuits zur Verfügung, so dass diese Bauteile wie elementare
Transistoren benutzt werden können. Leider existieren heute mehrere Spice-Varianten, die
von den Halbleiterherstellern nicht gleichermaßen unterstützt werden.
Obwohl es sich bei Spice um ein altes Programm handelt, ist Spice aufgrund der guten
Struktur und der einfachen Syntax auch heute noch interessant. Aufgrund verschiedener
Weiterentwicklungen und Erweiterungen kann Spice auch für moderne Schaltungen
verwendet werden. Auch neuere Simulatoren wie beispielsweise Saber oder Simplorer
verwenden keine prinzipiell anderen Algorithmen als Spice.
Spice wurde teilweise kommerziell verwertet, weshalb nicht alle Versionen frei verfügbar
sind. Eine sehr populäre Fassung ist die Version Spice2g6 (also die 7. Fassung von Spice2).
Auf dieser Version baut Spice3 auf, das heute in der Version Spice3f5 vorliegt. Gleichzeitig
entstanden eine Reihe von Erweiterungen bzw. Dialekten wie HSPICE, XSPICE und
PSpice (kommerzielle Version für PC). Insbesondere PSpice (Microsim Corp., jetzt Orcad
E K. Müller
Elektronik und Prozessmesstechnik
9
Hochschule Bremerhaven --- IAE
Inc.) ist weitgehend inkompatibel zu allen Weiterentwicklungen von Spice. Andere Firmen
wie Electronics Workbench (Multisimt) lehnen sich in ihren Produkten wieder an Spice3
an.
2.2.1
Digitale Simulatoren
Digitale Simulatoren arbeiten grundsätzlich anders als Simulatoren für analoge
Schaltungen. Ein digitaler Simulator wertet Erweiterungen boolscher Gleichungen aus und
arbeitet “ereignisdiskret”, d.h. die Ergebnisse werden jeweils für bestimmte Zeiten
berechnet (z.B. jeweils nach Gatterlaufzeiten). Die Beschreibung digitaler Systeme erfolgt
heute überwiegend in Hardwarebeschreibungssprachen (VHDL oder Verilog). Ein reales
System verfügt fast immer über analoge und digitale Komponenten.
3
Elementare Schaltungstechnik
Auch wenn heute leistungsfähige und komfortable CAD-Werkzeuge Unterstützung beim
Entwurf elektronischer Schaltungen bieten, so muss der Ingenieur doch über ein gewisses
Maß an Wissen über Schaltungstechnik verfügen, um die für eine bestimmte Aufgabe
geeignete Schaltung entwerfen zu können. Die Details der Schaltung sowie der Entwurf der
Leiterplatte kann dann im wesentlichen mit Software erledigt werden
3.1
Analyse linearer Netzwerke
Lineare beliebige Netzwerke lassen sich mit Hilfe der Knoten- und Maschengleichungen
sowie den Abhängigkeiten zwischen Strom und Spannung der Bauelemente in den Zweigen
des Netzwerkes berechnen.
Ein Netzwerk habe z Zweige und k Knoten. Dann existieren für die Ströme k---1
unabhängige Gleichungen (es existieren natürlich k Gleichungen aber nur, k---1 sind
linear unabhängig). Die noch fehlenden Gleichungen zur Bestimmung sämtlicher Ströme
in den Zweigen folgt aus den Maschengleichungen. Es existieren genau z---k+1
unabhängige Maschen. Aus dem sogenannten vollständigen Baum lassen sich diese
unabhängigen Maschengleichungen ermitteln. Werden in den Maschengleichungen die
Spannungen durch die Ströme in den einzelnen Zweigen (Ausnahme: ideale
Spannungsquellen) ersetzt, so folgen die Ströme als Lösung eines linearen Gleichungssystems.
Die Analyse von Netzwerken setzen wir als bekannt voraus, deshalb braucht hier nicht
weiter daraus eingegangen zu werden.
3.2
Quellenkonversion
Reale Spannungs- und Stromquellen lassen sich stets ineinander umrechnen. Die Wahl
einer geeigneten Darstellung kann eine Schaltung dramatisch vereinfachen.
E K. Müller
10
Elektronik und Prozessmesstechnik
Ri
E K. Müller
Hochschule Bremerhaven --- IAE
Ia
Elektronik und Prozessmesstechnik
Ia
Ri = 8Ω
11
Hochschule Bremerhaven --- IAE
Ia
RL = 47Ω
U0
Bild 1.7:
RL
Ua
I0
Ri
RL
Ua
Bild 1.9:
Spannungs- und Stromquelle mit Innenwiderstand
An den Anschlussklemmen sind die linke Schaltung (mit Spannungsquelle) und die rechte
Schaltung (mit Stromquelle) nicht zu unterscheiden. Für die Spannungsquelle erhält man
U − Ua
U
U
= 0− a .
Ia = 0
Ri
Ri
Ri
(1.22)
Der Zusammenhang zwischen Ausgangsspannung und Ausgangsstrom bei der Stromquelle
lautet
Ia = I0 −
Ua
.
Ri
(1.23)
Damit ist offensichtlich, dass bei gleichen Innenwiderständen Ri der Zusammenhang
I0 =
U0
Ri
(1.24)
Beispiel: Wie groß ist der Laststrom Ia im Lastwiderstand RL ?
Ia
RL = 47Ω
Ua
Schaltung mit Stromquelle
Die Aufgabe wird einfacher, wenn die Stromquelle mit Innenwiderstand durch eine
Spannungsquelle mit der Spannung
U 0 = R i I0 = 96mV
ersetzt wird (Bild 1.9).
Ua
Umwandlung in Spannungsquelle
Daraus folgt unmittelbar
Ia =
U0
) = 96mV = 1.745mA .
Ri + RL
55Ω
(1.26)
Natürlich hätte man das Problem auch mit Knoten- und Maschengleichung lösen können;
die Umwandlung von Spannungs- in Stromquelle ist jedoch eleganter.
4
Halbleiterbauelemente (aktive Bauelemente)
Das Verhalten aktiver Bauelemente kann durch enthaltene Spannungs- oder Stromquellen
beschrieben werden. Diese können ungesteuert (z.B. Diode) oder gesteuert (Transistor)
sein. Es lassen sich damit prinzipiell Schaltungen aufbauen, die eine Verstärkung > 1
aufweisen.
Erst mit zunehmender Temperatur lösen sich einzelne Elektronen aus dem Gitter und
bewirken eine (schlechte) Leitfähigkeit des Materials. Bei Metallen stellt sich eine
gegenteilige Wirkung ein, da mit zunehmender Temperatur durch eine vermehrte
Bewegung der Elektronen im Metall die Leitfähigkeit behindert wird.
Ri = 8Ω
Bild 1.8:
RL
Halbleiter gehören zur 4. Gruppe im Elementensystem. Es existieren jedoch auch
Verbindungen zwischen der 3. und der 5. Gruppe (III-V-Halbleiter), die die gleichen
elektronischen Eigenschaften aufweisen. Alle Halbleiter bilden sehr große Kristallgitter,
in denen die Elektronen best eingebunden sind. Es existieren also keine freien Elektronen
wie in Metallen. Reine Halbleiter gehören damit eher zu den Nichtleitern und haben
technisch keine Bedeutung.
gelten muss.
I0 = 12 mA
U0 = 96 mV
(1.25)
Der technisch wichtigste Halbleiter ist Silizium. Vereinzelt finden sich auch noch
Anwendungen mit Germanium bzw. sogenannte Hybridhalbleiter aus Germanium und
Silizium. In neuerer Zeit hat der Verbindungshalbleiter GaAs (Galliumarsenid) viel
Bedeutung erlangt (schnelle HF-Schaltungen, Optoelektronik).
4.1
Eigenleitung
Die Eigenleitung ist --- wie gesagt --- technisch bedeutungslos. Für das Verständnis der
Halbleiterbauelemente ist das Prinzip der Eigenleitung jedoch wesentlich. Halbleiter
E K. Müller
Elektronik und Prozessmesstechnik
12
Hochschule Bremerhaven --- IAE
E K. Müller
bilden ein regelmäßiges (dreidimensionales) Gitter, das jedoch zum Erläuterung der
Halbleitereigenschaften auch zweidimensional gezeichnet werden kann.
4+
4+
4+
4+
4+
4+
4+
4+
13
Elektronik und Prozessmesstechnik
Bild 1.11:
Hochschule Bremerhaven --- IAE
4+
5+
4+
4+
4+
4+
4+
4+
n-Dotierung eines Halbleiters
Dieses Prozess nennt man Dotierung. Der Halbleiter wird damit zu einem Leiter. Die
Leitfähigkeit hängt von Grad der Dotierung ab.
Bild 1.10:
Kristallgitter eines Halbleiters (z.B. Silizium, Selen, Germanium)
Zu dem vierwertigen Kern gehören jeweils 4 Elektronen. Das Kristallgitter entsteht nun
dadurch, dass Elektronenpaare bilden, die gewissermaßen von zwei Atomkernen
gleichermaßen genutzt werden. Unter dem Einfluß thermischer Energie können
Elektronen aus dem Verband entfernt werden, die sich dann vergleichbar mit freien
Elektronen bewegen können. Es bleibt eine Elektronenfehlstelle zurück.
Eine Elektronenfehlstelle bezeichnet man als Loch.
In einem eigenleitenden Halbleiter existieren gleich viele bewegliche Elektronen und
Löcher.
5-wertige Atome in einem Halbleiter nennt man Donatoren. Sie führen auf einen
n-Halbleiter, bei dem die Elektronen in der Überzahl sind.
In einem n-dotierten Halbleiter sind die Elektronen Majoritätsladungsträger und die
Löcher sind Minoritätsladungsträger.
4.2.2
Bringt man 3-wertige Atome (durch Diffusion) in den Halbleiter ein, so entstehen Löcher
(Elektronenfehlstellen).
Ein Loch kann man als “positiven Ladungsträger” auffassen, da das Ladungsgleichgewicht
nicht mehr besteht. Unter dem Einfluss eines elektrischen Feldes bewegen sich die
Elektronen entgegen der Feldrichtung. Gleichzeitig entsteht ein Löcherstrom in
Feldrichtung.
4.2
Dotierung (Störleitung)
Die Eigenschaften eines Halbleiters lassen sich technisch nutzen, wenn in dem reinen
Halbleiter gezielt Atome von 5- bzw. 3-wertigen Elementen eingebracht werden. Diese
Elemente nehmen im Kristallgitter die Plätze der Halbleiteratome ein.
4.2.1
n-Halbleiter (n-Dotierung)
Bringt man 5-wertige Atome (durch Diffusion) in den Halbleiter ein, so entstehen freie
Elektronen. Die Elektronen sind nicht in das Kristallgitter eingebaut.
p-Halbleiter (p-Dotierung)
Bild 1.12:
4+
3+
4+
4+
4+
4+
4+
4+
Loch
(positiv)
p-Dotierung eines Halbleiters
Diesen Prozess nennt man p-Dotierung. Der Halbleiter wird damit zu einem Leiter. Die
Leitfähigkeit hängt von Grad der Dotierung ab.
3-wertige Atome in einem Halbleiter nennt man Akzeptoren. Sie führen auf einen
p-Halbleiter, bei dem die Löcher in der Überzahl sind.
In einem p-dotierten Halbleiter sind die Löcher Majoritätsladungsträger und die
Elektronen sind Minoritätsladungsträger.
E K. Müller
14
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Die Leitfähigkeit kommt hier durch die Löcher zustande, die sehr leicht Elektronen
aufnehmen und auf diese Weise zu dem Transport von Ladungsträgern beitragen.
4.3
E K. Müller
15
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Raumladungsdichte
ρ
+
Diode (pn-Übergang)
Alle Halbleiterbauelemente basieren auf pn-Übergängen, bei dem p- und n-dotierte
Gebiete aufeinandertreffen. Das jeweilige Übergewicht an p- bzw. n-Ladungsträgern
gleicht sich in einem engen Gebiet durch Diffusion aus.
x
--Feldstärke
E
x
x
p
---
+
E=1
Á
n
x
Bild 1.13:
Der letzte Verlauf (Wegintegral über die Feldstärke) offenbart, dass sich über dem
pn-Übergang eine Spannung aufbaut.
Die Zone um den pn-Übergang ist elektrisch geladen. Es sind in dieser Zone jedoch kaum
freie Ladungsträger vorhanden, da sie in das Kristallgitter eingebunden sind.
---
0
Potenzial
Φ
pn-Übergang
Es entsteht um Übergang herum eine Raumladungszone durch die Abwanderung der
jeweiligen Majoritätsladungsträger. Dadurch sind die Zonen um den pn-Übergang nicht
mehr elektrisch neutral. Aufgrund der Trennung der Ladungsträger entsteht ein
elektrisches Feld. Die folgenden prinzipiellen Verläufe zeigt das Bild 1.14.
 Ã(ξ)dξ
x
Φ=−
 E(ξ)dξ
+
0
x
Bild 1.14:
Ladungsverteilung, Feldstärke und Potential beim pn-Übergang
(schematisiert)
Versieht man die Halbleiter mit einem Metallanschluss, entsteht das einfachste
Halbleiterbauelement: die Diode.
p
Die Zone um einen pn-Übergang bildet eine Sperrschicht.
---
+
n
Metallkonakte
Die Spannung aufgrund der Potenzialdifferenz am pn-Übergang bezeichnet man als
Diffusionsspannung.
Bild 1.15:
Aufbau einer Diode
Die Diode besteht somit aus einem Halbleiter-Halbleiter-Übergang mit unterschiedlicher
Dotierung. (Bei der Schottky-Diode verwendet man einem Metall-Halbleiter-Übergang.)
Das Bauteil besitzt folglich nur zwei Anschlüsse, die mit Anode (+-Pol) und Kathode
(----Pol) bezeichnet werden.
Anode A
Bild 1.16:
Kathode K
Symbol der Diode
Die Kathode ist oft durch einen Ring gekennzeichnet, da die Einbaurichtung für die
Funktion entscheidend ist.
E K. Müller
16
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
Bei positiver Anode gegenüber der Kathode fließt ein Strom; bei negativer Spannung
“sperrt” die Diode. Der statische Verlauf ID (UD ) wird durch folgende Exponentialfunktion
beschrieben

UD
I D = I S e mUT − 1

(1.27)
.
17
Elektronik und Prozessmesstechnik
max. Strom:
max. Sperrschicht-Temp.
max. Verlustleistung:
Hochschule Bremerhaven --- IAE
150 mA
175 0C
500 mW
Zeichnet man die Kennlinie (I-U-Diagramm) für die 1N4148, so erhält man einen fast
idealen Verlauf für eine Diode.
Id
Die Spannung UT ist die Temperaturspannung, die bei Zimmertemperatur ca.
25,5mV beträgt.
Durchlassbetrieb
Man rechnet in der Praxis auch gern mit folgender Beziehung

ID = IS e
UD
UT
−1

---100V
(1.28)
.
Sperrbetrieb
0.7V
Ud
Man setzt also m = 1 und nimmt dafür eine Temperaturspannung von UT = 40mV an.
Die grundsätzliche Funktion der Diode hängt natürlich von der Temperatur nicht ab; die
Kennlinie ist aber temperaturabhängig. Der “Korrekturfaktor hat einen Wert Im Bereich
von ca. 1..2. Die Kennlinie hat die in Bild 1.17 dargestellten Verlauf.
Strom Id
Bild 1.18:
Dioden-Kennlinie
Da die Diode den Strom nur in positiver Richtung führen kann, bezeichnet man
Dioden auch als Gleichrichter.
0.12
0.1
Leistungs-Dioden sind für Spannungen bis ca. 3kV und für Ströme bis ca. 4kA lieferbar. Die
elektrischen Daten sind für Leistungsdioden jedoch schlechter als die für Kleinsignaltypen.
0.08
0.06
Ein Betrieb der Diode bei Spannungen UD < ---USperr, max führt i.a. zur Zerstörung der
Diode (Ausnahme: Z-Diode). Die Spannung UD hängt im wesentlichen vom eingesetzten
Material ab (Si: UK ≈ 0,65V, Ge: UK ≈ 0,35V, Schottky: UK ≈ 0,3V). Die
Schottky-Diode (Metall-Halbleiter-Übergang) besitzt ein besonderes Symbol.
0.04
0.02
0
---0.02
kaputt
---5
---4
---3
---2
---1
0
1
2
Anode A
Spannung Ud
Bild 1.17:
Verlauf von Strom als Funktion der Spannung an der Diode
Man gibt als Kenngrößen gewöhnlich nicht m und UT an, sondern den praktischeren
Wert UD . Diese Spannung wird Flussspannung genannt; sie wird bei ID (ca. 0,1 Imax )
gemessen. Die Betriebsgrenzen sind Imax (bei positiver Spannung UD ) und ---USperr, max .
Die Daten der Diode 1N4148 (Kleinsignal-Diode) lauten:
Typ:
Silizium Epitaxial-Planardiode
Sperrstrom:
25 nA
max. Sperrspannung:
100 V
Bild 1.19:
4.3.1
Kathode K
Symbol der Schottky-Diode
Z-Diode
Zener-Dioden (Z-Dioden genannt) ist die Sperrspannung UZ genau festgelegt, d.h. ab
einer bestimmten Sperrspannung steigt der Sperrstrom. Diese Dioden werden als
Spannungsreferenz und zur Stabilisierung von Gleichspannungen benutzt. Z-Dioden sind
mit Durchbruchsspannungen im Bereich von ca. 3-200V erhältlich. Durch entsprechende
Schaltungen muss natürlich der Sperrstrom begrenzt werden, um die Z-Diode nicht zu
schädigen.
E K. Müller
Elektronik und Prozessmesstechnik
18
Anode A
Bild 1.20:
E K. Müller
Hochschule Bremerhaven --- IAE
19
Elektronik und Prozessmesstechnik
i
Kathode K
Hochschule Bremerhaven --- IAE
i
Symbol der Z-Diode
ideale Diode
u
Die Durchlassspannung unterscheidet sich nicht von der normaler Dioden. Ein
Güte-Kriterium ist der differenzielle Innenwiderstand
r Z = ∆U
∆I
u
r=
⇔
(1.29)
im negativen Durchlassbereich. Bei sehr kleinen Zener-Spannungen ist der differenzielle
Innenwiderstand recht groß, so dass sich diese Dioden nicht gut für Spannungsstabilisierungen eignen.
UT
ID
UK ≈ 0,7V
reale Diode
Bild 1.22:
Ersatzschaltbild
Ersatzschaltbild für eine reale Diode (Silizium)
Das Ersatzschaltbild enthält nun nur noch ideale Bauelemente.
Bild 1.21:
5
Kennlinie der Z-Diode (nach [2])
S
Ideale Diode: kein Sperrstrom, kein Spannungsabfall in Flussrichtung.
S
Idealer Widerstand: Spannungsabfall proportional zum Strom.
S
Ideale Spannungsquelle: Die Spannung ist unabhängig vom Strom (Knickspannung UK )
Mit diesen idealisierten Bauelementen folgt die Kennlinie in Bild 1.23.
I
Diodenschaltungen
Durchlassbetrieb
reale Kennlinie
Um Schaltungen mit Dioden einfach entwerfen zu können, wird häufig ein Modell der
Diode verwendet, dass die wesentlichen Eigenschaften der Diode richtig wiedergibt. Die
exakte exponentielle Kennlinie (1.27) ist für diesen Zweck i.a. ungünstig. Bewährt hat sich
das folgende Ersatzschaltbild der Diode.
Kennlinie für
Ersatzschaltbild
Sperrbetrieb
0.7V
Bild 1.23:
U
Kennlinien von realer Diode und vom Ersatzschaltbild (KIS = keep it simple)
Der Widerstand r in der Ersatzschaltung ist der differenzielle Widerstand, d.h. er hängt vom
Arbeitspunkt (Betriebspunkt der Diode) ab, da die Steigung der realen Kennlinie (1.27)
nicht konstant ist. Der differenzielle Widerstand wird als Kehrwert des Leitwerts
E K. Müller
20
Elektronik und Prozessmesstechnik

U
D
g = 1r = dI = d
I e mU T − 1
dU D
dU D S
E K. Müller
Hochschule Bremerhaven --- IAE

=
UD
IS
e mU T
mU T
(1.30)
bestimmt. Aus (1.27) folgt
Einweggleichrichterschaltung
(1.31)
I S e mUT = I D + I S .
und damit
g=
UD
I + IS
IS
I
e mUT = D
≈ D .
mU T
mU T
mUT
(1.32)
Gleichrichterschaltungen werden zur Erzeugung von Gleichspannung aus Wechselspannung eingesetzt (z.B. in Netzteilen). Das Eingangssignal ist also eine Wechselspannung
(AC); das Ausgangssignal ist ein Spannung, die nur noch positiv oder negativ ist.
i
Man erhält für den differenziellen Widerstand
r = 1g ≈
Hochschule Bremerhaven --- IAE
Technisch nutzt man der Änderung der Sperrschichtkapazität, um eine spannungsabhängige Kapazität zu erzeugen (z.B. in der Funktechnik).
5.2
UD
21
Elektronik und Prozessmesstechnik
mU T
.
ID
(1.33)
D
RL
~
U
UL
In der Praxis rechnet man mit m = 1 und UT = 40mV. Die Berechnung vereinfacht sich
dann zu
r≈
UT
.
ID
(1.34)
Die differenzielle Widerstand r sinkt also mit steigendem Diodenstrom ID .
5.1
Bild 1.25:
Falls die Wechselspannung U groß gegenüber der Knickspannung UK (ca. 0,7V bei
Silizium-Dioden) ist, ergibt sich ein Verlauf gemäß Bild 1.26.
U [V] 15
Dynamisches Verhalten
10
Unter dynamischem Verhalten versteht man die Eigenschaften eines Bauelementes für
“schnelle” Vorgänge, d.h. für hohe Frequenzen. Für sehr schnelle Vorgänge gilt für den
Zusammenhang zwischen Strom und Spannung nicht mehr die Kennlinie in Bild 1.18. Der
Grund liegt in in Kapazitäten, die im Sperrbetrieb durch Speicherung von Ladungsträgern
oder im Durchlassbetrieb durch Diffusion gebildet werden. Das Hochfrequenz-Ersatzschaltbild ist in Bild 1.24 gezeigt.
u
⇔
reale Diode
Bild 1.24:
5
u
---5
UT
ID
C
Ersatzschaltbild
Hochfrequenz-Ersatzschaltbild für die Diode (an einem Arbeitspunkt)
U
---10
---15
r=
UL
0
i
i
Einweggleichrichtung
Bild 1.26:
0
5
10
15
20
ωt [rad]
25
Ein- und Ausgangsspannungen des Gleichrichters
Die Ausgangsspannung wird nun nicht mehr negativ. Man benötigt jedoch häufig
“geglättete” Gleichspannungen. Die Aufgabe der Glättung übernehmen Kondensatoren,
die elektrische Energie speichern können. Die Schaltung in Bild 1.25 muss nur durch einen
Kondensator (größerer Wert, typisch Elko oder Tantalkondensator).
E K. Müller
22
Elektronik und Prozessmesstechnik
i
Bild 1.27:
D
E K. Müller
23
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Gelegentlich zeichnet man Brückengleichrichter auch in folgender Form, was natürlich mit
Bild 1.29 identisch ist.
C
~
U
Hochschule Bremerhaven --- IAE
RL
UL
iL
D1
iw
Einweggleichrichtung mit Glättung durch Kondensator
Die Ausgangsspannung UL verläuft nun wesentlich gleichmäßiger. Je größer der
eingesetzte Kondensator, desto besser erfolgt die Glättung der Spannung. Der Abfall der
Spannung ist wird durch die Entladung des Kondensators verursacht.
D3
~
U
RL
U [V] 15
D2
UL
D4
10
5
Bild 1.30:
UL
0
---5
Während der positiven Halbwelle der Wechselspannung leiten D1 und D4; während der
negativen Halbwelle führen D2 und D3 den Strom. Den Verlauf der Spannungen U und
UL zeigt Bild 1.31.
U
---10
---15
Bild 1.28:
5.3
0
5
10
15
20
ωt [rad]
25
U [V] 15
Ein- und Ausgangsspannungen des Gleichrichters
10
0
Nachteilig an der Einweggleichrichtung ist die schlecht Ausnutzung der Wechselspannung,
da während der negativen Halbwelle keine Gleichrichtung erfolgt. Diesen Nachteil hat der
Brückengleichrichter nicht.
D
D1
U
Bild 1.29:
~
Brückengleichrichter
---5
---15
D3
UL
U
---10
iL
RL
D2
UL
5
Brückengleichrichter
iw
Brückengleichrichter
Bild 1.31:
0
5
10
15
20
ωt [rad]
25
Ein- und Ausgangsspannungen des Brüpcken-Gleichrichters
D4
Die praktisch ausgeführte Gleichrichterschaltung zeigt Bild 1.32. Hier wird die
Ausgangsspannung wieder durch einen Kondensator geglättet. Ein fast perfekte
Gleichspannung erzeugt man dann mit weiteren elektronischen Bauelementen, die später
behandelt werden (Transistoren und Operationsverstärker).
E K. Müller
24
Elektronik und Prozessmesstechnik
D
iw
D1
Hochschule Bremerhaven --- IAE
iL
UL
Bild 1.32:
6
D2
~
U
RL
Brückengleichrichter mit Glättungsschaltung
Die Basis-Emitter-Strecke verhält sich wie eine gewöhnliche Diode, d.h. es fließt ein
Basisstrom iB nur bei positiver Spannung UBE . Das Verstärkungsprinzip wird deutlich,
wenn man die unterschiedlichen Dotierungen und Schichtdicken berücksichtigt.
Bipolartransistor
Der Bipolartransistor ist ein stromgesteuerter Verstärker, d.h. mit einem kleinen
Steuerstrom kann ein großer Strom eingestellt werden. Bauteile mit einer Verstärkereigenschaft heißen aktive Bauelemente.
Bipolartransistor: Strom fließt über PN-Übergänge.
Im Gegensatz dazu sind sogenannte Feldeffekttransistoren Unipolartransistoren. Der Strom
fließt nur durch ein Gebiet mit einer Dotierung (nur p- oder nur n-Gebiet).
n
Basis
RB
B
Emitter
iC
Für Minoriätsladungsträger ist eine Sperrschicht durchlässig.
Da Elektronen in der Basiszone Minoritätsladungsträger sind (die Basis ist ja p-dotiert)
können somit die Elektronen in die Kollektorzone gelangen. Diese Elektronen bilden den
positiven Kollektorstrom, der unter dem Einfluss des elektrischen Feldes zustande kommt.
p---
RC
C
B
Der Kollektorstrom ist zum Basisstrom proportional. Wichtigste Kenngröße des
Bipolartransistors ist die Stromverstärkung
∆
E
n+
E
Bild 1.33:
Der Basisstrom iB bewirkt einen Elektronenstrom vom Emitter (daher der Name) in die
Basiszone. Der Elektronenstrom ist umso stärker, je größer die Dotierung des
Emitterbereichs gewählt wird. Aufgrund der geringen Dotierung und der geringen
Ausdehnung der Basiszone gelangen sehr viele Elektronen in den Kollektorbereich. Die
Elektronen können die Basis-Kollektor-Sperrschicht ungehindert überwinden.
Der Basisstrom injiziert einen Kollektorstrom, der größer als der Basisstrom ist.
Kollektor
iB
Hochschule Bremerhaven --- IAE
Die Dicke der Basisschicht ist außerordentlich gering (ca. 100μm). Durch die
unterschiedlich starken Dotierungen dürfen Emitter und Kollektor nicht vertauscht
werden, obwohl die Zonenfolge im Prinzip eine Umkehrung gestatten würde. Die Breite
der Schichten und den Grad der Dotierung bestimmen die Eigenschaften der
verschiedenen Transistortypen.
D4
C
25
gefolgt von einer schwach dotierten Basis-Zone (p---). Der Kollektorzone ist wieder
n-dotiert. Die pn-Übergänge zwischen Basis und Emitter und zwischen Basis und Kollektor
bilden Diodenstrecken. Da diese Dioden gegensinnig angeordnet sind, kann der Transistor
zwischen Kollektor und Emitter keinen Strom führen, wenn kein Basisstrom iB fließt.
D3
C
E K. Müller
Elektronik und Prozessmesstechnik
Aufbau eines NPN-Transistors (Anschluss: Emitterschaltung) und Symbol
Der bipolare Transistor (NPN-Typ) besteht aus einer Folge von unterschiedlich dotierten
Halbleiterzonen (heutzutage Silizium). Die untere Zone (Emitter) ist stark n-dotiert (n+),
h fe = β =
iC
.
iB
(1.35)
Die Bezeichnungen hfe oder β sind für die Stromverstärkung gebräuchlich. Die
Stromverstärkung variiert in einem weiten Bereich und liegt bei Leistungstransistoren bei
etwa β = 5 bis β = 500 bei NF-Transistoren. Aus (1.35) folgt, dass der Kollektorstrom im
wesentlichen nur vom Basisstrom und nicht von der Kollektor-Spannung abhängt. Bei
realen Transistoren besteht jedoch auch eine geringe Abhängigkeit von der
Kollektor-Emitter-Spannung.
Betreibt man den NPN-Transistor in folgender Messschaltung (Bild 1.34), so kann das
sogenannte Kennlinienfeld des Transistors gemessen werden.
E K. Müller
26
Elektronik und Prozessmesstechnik
iB
C
Hochschule Bremerhaven --- IAE
A
E K. Müller
iC
B
27
Elektronik und Prozessmesstechnik
iB
uC
E
uBE
0.7V
Bild 1.36:
Bild 1.34:
Messung des Kennlinienfeldes
Mit der Stromquelle an der Basis wird ein konstanter Basisstrom iB eingestellt und die
Kollektorspannung uC wird jeweils variiert. Der Kollektorstrom als Funktion der
Kollektor-Emitter-Spannung mit iB als Parameter bildet das Kennlinienfeld des
Bipolartransistors (Bild 1.35).
iC
Verlustleistungshyperbel
Eingangskennlinie des Transistors
Die in Bild 1.35 eingezeichnete Hyperbel kennzeichnet das Gebiet, in dem der Transistor
dauerhaft betrieben werden darf. Die Verlustleistung ist das Produkt von Kollektor-Strom
und Kollektor-Emitter-Spannung
(1.36)
P V = u C iC .
Eine maximale Verlustleistung darf nicht überschritten werden, da ansonsten der
Transistor durch Überhitzung Schaden nimmt (max. Temperatur des Siliziums ca. 150 0C).
Der maximale Strom folgt aus (1.36) durch Auflösung nach
IB 5
IB 4
i C,max =
IB 3
P V,max
uC .
(1.37)
Diese Beziehung ist grafisch in Bild 1.35 eingezeichnet (gestrichelt).
IB 2
IB 1
6.1
0 < i B1 < i B2 < i B3 < i B4 < i B5
uC
Bild 1.35:
Hochschule Bremerhaven --- IAE
Kennlinienfeld des Bipolartransistors
Bestimmung des Arbeitspunktes
Der Verlauf von Strom und Spannung am Transistor ist nichtlinear, d.h. Strom und
Spannung sind nicht proportional. Damit kann der Arbeitspunkt eines Transistors in einer
Schaltung mit einem Widerstand nicht mehr analytisch ausgerechnet werden. Der
Arbeitspunkt kann aber leicht grafisch ermittelt werden.
Man bezeichnet das Diagramm in Bild 1.35 auch als Ausgangskennlinienfeld des
Transistors. Die Eingangskennlinie, d.h. das Diagramm des Basisstroms über der
Basisspanung ist einfach eine Diodenkennlinie. Aufgrund der Dotierungsverhältnisse darf
dieser Übergang jedoch nicht bei hohen negativen Spannungen betrieben werden.
RC
iB
C
B
uR
uC
iC
U0
E
Bild 1.37:
Arbeitspunkt der Schaltung aus Widerstand und Transistor
E K. Müller
Elektronik und Prozessmesstechnik
28
E K. Müller
Hochschule Bremerhaven --- IAE
Elektronik und Prozessmesstechnik
Der Spannungsumlauf in der rechten Masche liefert
C
(1.38)
uC + uR − U0 = 0 .
Die Spannung am Widerstand kann durch den Strom ausgedrückt werden
Kollektor
p
(1.39)
uC + R C iC − U 0 = 0 .
iB
Damit lautet der Zusammenhang zwischen iC und uC
iC =
U0 − uC
.
RC
RB
(1.40)
iC
U − uC
iC = 0
RC
iC0
Arbeitspunkt
IB 3
uC
Grafische Bestimmung des Arbeitspunktes
In Bild 1.38 ist der Schnittpunkt von der Widerstandsgeraden mit der Transistorkennlinie
für den Basisstrom iB4 markiert. Im Arbeitspunkt stellen sich eindeutig der Strom iB0
sowie die Spannung uC0 ein. Nur im Schnittpunkt werden die Gleichung der
Widerstandsgeraden und die Kennlinie des Transistors gleichzeitig erfüllt.
6.2
C
B
E
p+
Aufbau eines PNP-Transistors (Anschluss: Emitterschaltung) und Symbol
NPN- und PNP-Transistoren mit vergleichbaren Werten bezeichnet man als
Komplementärtransistroren.
0 < i B1 < i B2 < i B3 < i B4 < i B5
Bild 1.38:
RC
Durch die unterschiedlichen Dotierungen bei NPN- und PNP-Transistoren ermöglichen
einen flexiblen Einsatz der Transistoren an positiven und negativen Spannungen.
IB 2
u0
iC
Der Basisstrom iB führt beim PNP-Transistor zu einer Injektion eines Löcherstroms vom
Emitter in den Kollektor, der die Sperrschicht zwischen Basis und Kollektor überwinden
kann (die Löcher sind ja Minoritätsladungsträger in der n-Basis).
IB 4
IB 1
uC0
n---
Hochschule Bremerhaven --- IAE
E
Bild 1.39:
IB 5
Widerstandsgerade
B
Emitter
Der Zusammenhang ist eine Gerade mit der Steigung ---1 / RC . Zeichnet man diese
Gerade in das Kennlinienfeld ein, so erhält man durch den Schnittpunkt dieser Gerade mit
der jeweiligen Transistorkennlinie den sogenannten Arbeitspunkt.
u0
RC
Basis
29
PNP-Transistor
Vertauscht man die Dotierungen, so entsteht ein PNP-Transistor. Die Richtungen von
Strom und Spannung müssen ebenfalls getauscht werden.
Mit komplementären Transistoren lassen sich beispielsweise Leistungsendstufen für
Verstärker aufbauen.
Die elektrischen Eigenschaften von NPN-Transistoren sind besser als die von
PNP-Transistoren. Dies liegt an der Beweglichkeit der Ladungsträger. Bei NPN-Transistoren sind dies die Elektronen; bei PNP Transistoren beruht die Leitfähigkeit auf
Löcherleitung. Da die Beweglichkeit der Elektronen deutlich höher als die der Löcher ist,
bevorzugt man NPN-Transistoren.
Ü1
Berechnung einer Transistorschaltung
Eine Berechnung von Transistorschaltungen ist möglich, wenn ein idealisiertes
Transistormodell verwendet wird. Eine genaue Analyse der Schaltung kann dann durch
Simulation mit einem vollständigen Transistormodell erfolgen.
E K. Müller
30
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Idealisiertes Modell:
Konstante Stromverstärkung β,
S
Konstante Basis-Emitterspannung von uBE = 0,7V,
S
keine Abhängigkeit des Kollektorstroms von der Kollektor-Emitter-Spannung (horizontale Geraden in Bild 1.38).
Arbeitspunkt für einen NPN-Transistor in
Emitterschaltung
Der Arbeitspunkt (Spannung uC und Strom iC ) der folgenden Schaltung soll ermittelt
werden.
u0
iB
RB
Feldeffekttransistoren besitzen für viele Anwendungen bessere elektrische Eigenschaften
als Bipolartransistoren. Am Ende dieses Abschnitts können beide Transistortypen
verglichen werden.
Feldeffekttransistoren können als spannungsgesteuerte Widerstände aufgefasst werden.
7.1
Sperrschicht-FET (JFET = Junction Field Effect
Transistor)
C
Sperrschicht
D
B
uC
uB 0
G
p+
n
Berechnung des Arbeitspunktes
Bekannt sind: ub0 = 5V, u0 = 20V, RC = 680Ω, RB = 100kΩ, β = 260.
a)
Wie groß ist der Basisstrom iB ? Hinweis: diese Teilaufgabe können Sie ohne die
rechte Maschengleichung lösen.
b)
Welchen Wert hat der Kollektorstrom iC ?
c)
Wie groß ist die Spannung uC am Kollektor des Transistors?
d)
Welche Verlustleistung nimmt der Transistor auf?
Kontrollergebnis: Die Verlustleistung in d) beträgt 138,6mW.
7
Feldeffekttransistoren
Die Idee zum Aufbau von Feldeffekttransistoren ist älter (Patent von J. Lilienthal, 1928)
als die Theorie der Bipolartransistoren. Jedoch gelang es erst 10 Jahre nach den ersten
S
G = Gate
D = Drain
S = Source
p+
E
G
uDS
Bild 1.40:
Hochschule Bremerhaven --- IAE
Bei einem Sperrschicht-FET wird der Widerstand durch die Änderung der Breite eines
leitfähigen Kanals variiert.
iC
RC
31
Bipolartransistoren funktionierende Feldeffekttransistoren aufzubauen (ca. 1960).
Feldeffekttransistoren sind spannungsgesteuerte Bauelemente (im Gegensatz zu den
stromgesteuerten Bipolartransistoren). Das Funktionsprinzip der FETs ist vergleichbar mit
Elektronenröhren, auf die hier aber nicht mehr eingegangen werden soll.
S
Ü1.1
E K. Müller
Elektronik und Prozessmesstechnik
Bild 1.41:
D
uGS
G
S
n-Kanal Sperrschicht-FET und Symbol
Die Anschlüsse des JFETs sind Source (Quelle), Drain (Senke) und Gate
(Steuerelektrode). Mit der Spannung des Gates gegenüber dem Source kann die Breite der
Sperrschicht verändert werden. Der Pfeil am Gate kennzeichnet die Richtung der “Diode”,
die durch das Gate und die Drain-Source-Strecke gebildet wird.
Der JFET ist selbstleitend, d.h. es besteht eine leitfähige Verbindung zwischen Drain
und Source, wenn die Spannung uGS = 0 ist.
Der JFET in Bild 1.41 wird mit negativer Spannung uGS betrieben. Bei negativer Spannung
verbreitert sich die Sperrschicht, d.h. der “Kanal” (Channel) zwischen Drain und Source
wird kleiner.
Die Ansteuerung von FETs durch das Gate erfolgt leistungslos.
Da die Gate-Diode in Sperrrichtung betrieben wird, fließt praktisch kein Strom in der
Gate-Leitung (vernachlässigbarer Sperrstrom).
E K. Müller
32
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
33
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
iD
iD
UGS 5
UGS 4
RD
UGS 3
u0
UGS 2
UGS 1
U P < u GS1 < u GS2 < u GS3 < u GS4 < u GS5 < 0
uG
uDS
Bild 1.42:
Bild 1.44:
Messschaltung für einen n-Kanal JFET
In der Schaltung in Bild 1.42 misst man folgende Verläufe des Drainstromes als Funktion
der Spannung uDS .
iD
Bild 1.43:
Man erkennt, dass der Drainstrom in einem weiten Bereich unabhängig von der Spannung
uDS ist und nur von der Steuerspannung uGS abhängt. Der FET ist damit ein
spannungsgesteuertes Bauelement.
Wie kommt es bei dem JFET zu den Bereichen konstanten Stroms (horizontale Verläufe
in Bild 1.44)? Zum Verständnis der Funktion ist es wesentlich, den Verlauf der Sperrschicht
im JFET zu kennen. Die Sperrschicht ist umso breiter, je größer die (Sperr-) Spannung an
dieser Schicht ist. Diese Sperrspannung ist aufgrund der relativ hohen Spannung am Drain
gegenüber dem Source innerhalb des JFET aber nicht konstant. Im Bereich des Drains ist
die Sperrspannung größer und somit die Sperrschicht breiter.
iDSS
Sperrschicht
uGS
UP
D
Drainstrom als Funktion der Gatespannung uGS (uDS konstant)


u GS
UP
G
p+
n
G
2
.
(1.41)
Zu beachten ist, dass sowohl die Gatespannung uGS als auch die Spannung UP negativ
ist.
Die Spannung UP heißt Pinch-Off-Spannung. Bei einer Spannung uGS < UP fließt
kein Drainstrom mehr.
Verändert man die Spannung uDS bei jeweils konstanter Gatespannung uGS , so erhält man
das Ausgangskennlinienfeld des JFET (Bild 1.44).
+
Bild 1.45:
S
p+
iD
Der Drainstrom steigt etwa quadratisch mit der Gatespannung an
i D = I DSS 1 −
Kennlinienfeld des JFET mit uGS als Parameter
uDS
---
uGS
Verlauf der Sperrschichten im JFET unter Spannung
Wird die Drainspannung erhöht, so verbreitert sich die Sperrschicht mit der Folge, dass sich
der leitfähige Kanal verengt. Bei kleinen Drainspannungen erhöht sich der Strom
proportional zur Spannung, d.h. der JFET verhält sich wie eine Widerstand
(Anlaufbereich). Bei größeren Spannungen kann durch die Verengung des Kanals der
Strom nicht weiter erhöht werden (horizontaler Bereich der Kennlinie). Der Drainstrom
iD hängt dann nur noch von der Gatespannung uGS ab.
E K. Müller
34
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
E K. Müller
Jetzt wird auch die Bedeutung der Pinch-Off-Spannung UP deutlich: Bei dieser
Gatespannung berühren sich die Sperrschichten und kein Drainstrom kann mehr fließen.
n-Kanal
p-Kanal-JFET
Hochschule Bremerhaven --- IAE
uDS
D
G
7.2
35
Elektronik und Prozessmesstechnik
S
uGS
D
Durch Vertauschen der Dotierungen erhält man einen p-Kanal-JFET, der mit Spannungen
umgekehrter Polarität betrieben wird.
iD
n+
SiO2
n+
G
p-Substrat
S
RD
D
u0
G
S
uGS
Bild 1.46:
Spannungen zum Betrieb des p-Kanal Sperrschicht-FET
Die Pfeilrichtung in dem Symbol für den p-Kanal-JFET steht für die Richtung der
Gate-Source-Diode, die wie bei dem n-Kanal-JFET in Sperrrichtung betrieben wird.
8
MOSFETs (=Metal-Oxyde Semiconductor FET)
Bei einem MOSFET ist wird Gate nicht über eine Sperrschicht sondern mit Hilfe einer
dünnen Lage aus SiO2 (Siliziumdioxyd) isoliert. Unabhängig von der Polarität der
Gatespannung kann somit stationär kein Strom im Gate-Anschluss fließen. Der MOSFET
ist somit ein ideales spannungsgesteuertes Bauelement. Im Gegensatz zum JFET ist der
MOSFET selbstsperrend. Auf die weniger bedeutsamen selbstleitenden MOSFETs
(Depletion MOSFETs) soll hier nicht eingegangen werden.
Bild 1.47:
n-Kanal-MOSFET und Symbol
In einem p-Substrat werden zwei n+-Inseln eindiffundiert und metallisiert (schwarze
Flächen). Diese Anschlüsse bilden Drain und Source. In der Regel verbindet man das
Substrat mit dem Source-Anschluss (untere Fläche). Wie durch die internen Dioden
angedeutet, kann zwischen Drain und Source kein Strom fließen, da immer eine Diode in
Sperrrichtung betrieben wird.
Der Gate-Anschluss ist über eine dünne Schicht aus SiO2 vollständig von der
Halbleiterstruktur isoliert. Über die Gate-Source-Spannung uGS wird ein elektrisches
Feld erzeugt, dass einen Einfluss auf die Ladungen auf dem Gate und dem Kanal unter der
Gateelektrode hat.
Bei positiver Spannung uGS werden negative Ladungen unter der SiO2-Isolation erzeugt
(influenziert), die einen leitfähigen Kanal bilden. Über die Gatespannung kann also die
Leitfähigkeit gesteuert werden. Obwohl sich unterhalb des Gates eine p-Schicht befindet
bildet sich ein leitfähiger Kanal durch Elektronenleitung aus (daher der Name
n-Kanal-MOSFET).
Da der Strom nur die eine Art von Ladungsträgern zustande kommt (Elektronen beim
n-Kanal-FET, Löcher beim p-Kanal-FET) spricht man von unipolarer Leitung. Beim
Bipolartransistor sind immer Löcher und Elektronen beteiligt.
Die Leitung des Stroms erfolgt unipolar in einem FET.
Feldeffekttransistoren sind aufgrund der unipolaren Leitung rauschärmer als Bipolartransistoren, was für NF- und HF-Verstärker besonders wichtig ist.
Für den Zusammenhang von Drainstrom und Gatespannung gilt der gleiche
Zusammenhang (1.42)
E K. Müller
36
Elektronik und Prozessmesstechnik
i D = I DSS


u
1 − GS
UP
E K. Müller
Hochschule Bremerhaven --- IAE
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
VDD
2
(1.42)
.
37
p-Kanal-MOSFET
T2
Allerdings sind nun beide Spannungen uGS und UP positiv. Die Gleichung (1.42) gilt
allerdings nur für uGS ≥ UP ; für uGS < UP kann nur ein verschwindend kleiner
Drainstrom fließen.
U2
U1
T1
iD
n-Kanal-MOSFET
iDSS
VSS
Bild 1.49:
UP
Bild 1.48:
2 UP
uGS
Drainstrom als Funktion der Gatespannung uGS (uDS konstant)
Das Ausgangskennlinienfeld, d.h. der Zusammenhang zwischen uDS und iD unterscheidet
sich nicht von dem eines JFET (Bild 1.44). Auch hier ist der Drainstrom iD weitgehend
unabhängig von der Drainspannung uDS . Die Höhe des Stroms lässt sich leistungslos über
die Gatespannung uDS einstellen. Die Abhängigkeit ist allerdings nichtlinear; der Strom
steigt quadratisch mit der Gatespannung an.
Durch Vertauschen der Dotierungen entsteht der p-Kanal-MOSFET. Alle Spannungen
müssen für den Betrieb des p-Kanal-MOSFETs umgekehrte Polarität aufweisen.
N-Kanal-MOSFETs werden auch für große Leistungen hergestellt. Ein Leistungs-MOSFET besteht dann aus ca. 6000 Einzeltransistoren (parallelgeschaltet) auf einem Substrat.
8.1
CMOS (=Complementary MOS)
MOSFETs eignen sich sehr gut für den Aufbau integrierter Schaltungen (IC = Integrated
Circuit), da sie nur einen Diffusionsschritt erfordern. Für komplexe Schaltungen verwendet
man n- und p-Kanal-MOSFETs auf einem Siliziumchip. Diese Technik wird für
Digitalschaltungen benutzt. Man erhält sehr kleine Strukturen und einen geringen
Leistungsbedarf durch die leistungslose Ansteuerung.
CMOS-Beispiel: Inverter für die Digitaltechnik
Der Inverter aus Bild 1.49 besteht aus einem p-Kanal- und einem n-Kanal-MOSFET. Die
positive Betriebsspannung bezeichnet man mit VDD (von Drain), die negative
Betriebsspannung (üblicherweise auch Masse gennant, 0V) wird mit VSS (von Source)
bezeichnet. Typische Werte für VDD sind 5V oder 3,3V.
Bei dieser Schaltung nimmt U1 nur die Werte VSS oder VDD an. Ist U1 = VSS (U1 = 0V)
ist der obere Transistor T2 leitend, T1 ist nicht leitend. Somit nimmt U2 den Wert VDD
an. Für U1 = VDD gilt umgekehrt U2 = VSS (U2 = 0V).
9
Berechnung von Halbleiterschaltungen
Berücksichtigt man alle Details eines Halbleiterbauelementes, so ist eine Berechnung von
Halbleiterschaltungen schwierig oder gar unmöglich. Da Bauelemente eines Types stets
großen Schwankungen unterworfen sind, wäre diese Vorgegehensweise auch zweifelhaft.
Für den praktischen Einsatz von Halbleiterbauteilen verwendet man deshalb “Modelle”.
Die verwendeten Modelle werden dabei soweit vereinfacht, dass nur noch die wesentlichen
Eigenschaften richtig wiedergegeben werden.
Modelle werden soweit wie möglich vereinfacht.
Es existiert somit nicht ein Modell für einen bestimmten Halbleiter, sondern man setzt ein
der Aufgabe angemesses einfaches Modell ein. Diese Vorgehensweise ist typisch für
Ingenieure. Auch in anderen Bereichen (Mechanik, Regelungstechnik usw.) werden
vereinfachte Modelle eingesetzt. Mechanische Beispiele sind “masselose Federn”,
“reibungsfreie Lager”, “Punktmassen” usw. Diese Modelle eigenen sich jedoch
ausgezeichnet, um das wesentliche Verhalten eines Systems richtig zu beschreiben.
E K. Müller
38
Elektronik und Prozessmesstechnik
9.1
E K. Müller
Hochschule Bremerhaven --- IAE
Elemente elektronischer Modelle
IA
Die Anzahl der Elemente zur Modellierung elektronischer Schaltung ist außerordentlich
klein; die meisten sind uns inzwischen bekannt:
Spannungsquellen, Stromquellen, Widerstände, Kondensatoren, Induktivitäten.
Bild 1.53:
Induktivitäten folgen später im Buch, sie spielen eine wichtige Rolle bei Hochfrequenzschaltungen und in der Leistungselektronik bzw. der Energieversorgung. Diese Elemente
genügen, um beliebige Halbleiter zu modellieren.
9.2
Gesteuerte Quellen
I
I, U
α UE
Hochschule Bremerhaven --- IAE
IA = α ⋅ UE
Spannungsgesteuerte Stromquelle
IA
Bild 1.54:
α ΙE
IA = α ⋅ IE
Stromgesteuerte Stromquelle
Die Bilder 1.51 bis 1.54 zeigen die möglichen Kombinationen von Quellen und
Steuerungen sowie die Abhängigkeiten der Ausgangsgröße von den Eingangsgrößen. Im
allgemeinen Fall kann die Abhängigkeit beliebig nichtlinear sein, d.h für Spannungsquellen
gilt
Bisher haben wir ungesteuerte Strom- und Spannungsquellen kennengelernt.
I, U
39
Elektronik und Prozessmesstechnik
I
(1.43)
U A = f (U E, I E)
U
U
und für Stromquellen
(1.44)
I A = f (U E, I E) .
Bild 1.50:
Ungesteuerte Strom- und Spannungsquellen mit Kennlinien
Ungesteuerte Quellen liefern einen konstanten Strom bzw. eine konstante Spannung. Der
Strom hat keinen Einfluss auf die Spannungsquelle; die Spannung an einer Stromquelle hat
keinen Einfluss auf den Strom.
Bei einer gesteuerten Spannungsquelle ist die Spannung abhängig von einer externen
Größe. Diese Größe ist entweder wieder eine Spannung oder ein Strom. Entsprechend
spricht man von einer
spannungsgesteuerten Spannungsquelle
oder von einer
stromgesteuerten Spannungsquelle.
UA
Bild 1.51:
UA
Bild 1.52:
α UE
UA = α ⋅ IE
Stromgesteuerte Spannungsquelle
Diode
Das einfachste Modell, das für viele Anwendungen aber ausreichend ist, besteht in einem
Schalter mit spannungsabhängiger Schalterstellung. Für U < 0 ist der Schalter offen, sonst
ist er geschlossen.
I
U, I
UA = α ⋅ UE
Spannungsgesteuerte Spannungsquelle
α ΙE
9.3
U<0
U≥0
Bild 1.55:
U
Modell einer idealen Diode
Bei einer negativen Spannung an der Diode fließt kein Strom; die Spannung ist von der
umgebenden Schaltung abhängig. Anderenfalls ist die Spannung null bei einem beliebigen
Strom in positiver Richtung.
Wird ein detaillierteres Modell benötigt, so kann das Modell in Bild 1.55 um einen
Widerstand und eine Spannungsquelle erweitert werden.
E K. Müller
40
Elektronik und Prozessmesstechnik
I
U, I
U, I
Bild 1.56:
Ud
Rd
Ud
Für folgende Schaltung sollen Kollektorstrom IC und Kollektorspannung UC bestimmt
werden.
U
R2
Modell einer realen Diode
U = U d + R d I = 0.5V + 16Ω 20mA = 0.82V .
Bipolartransistor
Bild 1.58:
Der Bipolartransistor wirkt damit als stromgesteuerte Stromquelle.
IB
IC
C
IC
U0
Schaltung mit NPN-Bipolartransistor
Daten der Schaltung: U0 = 20V, R1 = 270Ω, R2 = 87kΩ.
Daten des Transistormodells: β = 200, UD = 0.7V, RB = 240Ω, RC = 60kΩ.
a)
Wie groß ist der Basisstrom IB ?
b)
Bestimmen Sie die Kollektorspannung UC sowie den Kollektorstrom IC .
Lösungen: IB = 221.2μA, IC = 44.4mA,
IC
IB 4
IB 3
RB
βI B
R1
UC
IB
(1.45)
Der Bipolartransistor besteht aus einer Diodenstrecke zwischen Basis und Emitter. Der
Kollektorstrom folgt dann aus dem Basisstrom und der Stromverstärkung β.
B
RC
Ud
IB 2
IB 1
9.4.2
Übung: Verstärkungsunempfindliche Einstellung des Kollektorstroms
R2
UC
IC
U0
E
UCE
Modell (Ersatzschaltbild) des NPN-Bipolartransistors für positive Spannungen und Kennlinienfeld des Modells
Man erkennt, dass das Kennlinienfeld mit dem Modell des Transistors gut wiedergegeben
wird. Der Sättigungsbereich (an der IC -Achse für kleine Spannungen UC ) wird allerdings
nicht richtig modelliert. Das Modell in Bild 1.57 darf also nicht für Schaltungen benutzt
werden, in denen der Transistor in diesem Bereich betrieben wird.
Sättigungsbereich: Bereich in dem der Kollektorstrom kleiner ist als β IB .
UC = 8.02V.
Die Schaltung in Bild 1.58 hat den Nachteil, dass der Kollektorstrom von der
Stromverstärkung β abhängt. Die Stromverstärkung ist bei Transistoren aber starken
Schwankungen unterworfen. Bei der folgenden Schaltung wirken sich Schwankungen der
Stromverstärkung durch Exemplarstreuungen nur wenig auf den Kollektorstrom aus.
IB = 0
Bild 1.57:
Hochschule Bremerhaven --- IAE
Übung: Berechnung des Kollektorstroms mit Transistormodell
Beispiel: Welche Spannung fällt an einer Diode mit Ud = 0.5V und Rd = 16Ω ab, wenn
ein Strom von 20mA fließt?
9.4
41
Elektronik und Prozessmesstechnik
9.4.1
1
Rd
U<0
U≥0
E K. Müller
Hochschule Bremerhaven --- IAE
R3
Bild 1.59:
R1
Robuste Einstellung des Kollektorstroms (unempfindlich bezüglich der
Stromverstärkung)
E K. Müller
42
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
ID
IDSS
Daten der Schaltung: U0 = 15V, IC = 100mA, R2 = 1kΩ , R3 = 400Ω .
Daten des Transistormodells: β = 200, UD = 0.7V, RB → 0, RC → ∞.
a)
Wie groß muss R1 gewählt werden, damit der Strom IC den Wert 100mA
annimmt? Sie brauchen keine Rücksicht auf die E12-Reihe nehmen (z.B. durch
eine Realisierung von R1 als Potentiometer).
b)
Der Transistor wird durch einen anderen Transistor ersetzt, der nur über eine
Stromverstärkung von β = 100 verfügt. Welcher Kollektorstrom IC stellt sich nun
ein (mit dem Widerstand R1 aus a) )?
Lösungen: R1 = 34.26Ω , β = 100: IC = 95.7mA, β = 400: IC = 102.3.
9.5
Bei einem JFET wird die Gate-Source-Diode in Sperrrichtung betrieben. Es fließt somit
kein Gatestrom.
Der JFET wirkt damit als spannungsgesteuerte Stromquelle.
Für den Zusammenhang zwischen Drainstrom und Spannung gilt die Beziehung (1.46)
I D = I DSS


2
(1.46)
.
UGS = 0
UGS = 0.5Up
UGS = 0.75Up
UGS = Up
UDS
Kennlinienfeld des Modells für einen JFET
Im Bereich kleiner Drain-Source-Spannungen UDS gilt das Modell nicht. Sofern der
Transistor bei diesen Spannungen nicht betrieben wird, beschreibt das Modell das
sogenannte stationäre Verhalten (d.h. bei Gleichspannung und Gleichstrom) recht gut.
Man erkennt auch gut die nichtlineare (quadratische) Abhängigkeit des Drainstroms von
der Spannung UGS .
Genaue Modelle für JFETs (z.B. Shichman-Hodges-Modell im Spice-Simulator) besitzen
14 Parameter und ermöglichen die Simulation in allen Arbeitsbereichen.
9.5.1
Übung: Spannung und Strom in einem n-JFET
Für die folgenden Schaltung mit einem JFET sollen der Widerstand R1 für einen
Drainstrom ID = 3mA entworfen werden. Weiterhin ist die Spannung UDS zu bestimmen.
ID
Man kann das Verhalten des JFETs somit durch das vereinfachte Modell in Bild 1.60
beschreiben.
R2
D

I D = I DSS 1 −
G
Hochschule Bremerhaven --- IAE
UGS = 0.25Up
Bild 1.61:
JFET
u
1 − GS
UP
43
Elektronik und Prozessmesstechnik

u GS
UP
2
UDS
UGS
UGS
U0
R1
S
Bild 1.60:
Vereinfachtes Modell des JFET (Konstantstrombetrieb)
Zu diesem Modell gehört das folgende Kennlinienfeld.
Bild 1.62:
Dimensionierung einer Schaltung mit JFET
Die Daten des JFET-Modells sind: IDSS = 10mA, UP = ---3V.
Der Widerstand R2 sei 2.7kΩ . Die Spannung betrage U0 = 15V.
E K. Müller
Elektronik und Prozessmesstechnik
44
a)
Wie groß muss R1 gewählt werden?
b)
Welchen Wert hat die Spannung UDS ?
Hochschule Bremerhaven --- IAE
10.1
Verwendung eines JFET als Spannungsverstärker
(Wechselspannungen)
Erweitert man die Schaltung in Bild 1.62 (mit den bisher berechneten Werten) um
Kondensatoren, so entsteht ein Verstärker für Spannungen mit der Verstärkung A ≈ 10.
Die Ausgangsspannung
Ua
ist dabei um diesen Faktor
größer als die
Die Schaltung soll nicht weiter analysiert werden, da
Eingangsspannung Ue .
Wechselstromschaltungen mit Kondensatoren erst später behandelt werden.
ID
Das Kenntnis des Großsignalverhaltens ist jedoch auch erforderlich, um einen bestimmten
Arbeitspunkt (s. Bild 1.64) einzustellen, der für das Kleinsignalverhalten benötigt wird.
iC
10
∆U
U0
UA
∆I
U − uC
iC = 0
RC
IB 3
IB 2
IB 1
0 < i B1 < i B2 < i B3 < i B4 < i B5
RG
R1
C2
uC0
Bild 1.64:
Bild 1.63:
IB 4
Arbeitspunkt
UDS
IB 5
Widerstandsgerade
iC0
C3
UE
Großsignalverhalten
Dies wird benötigt bei Transistoren im Schaltbetrieb, d.h. bei Transistoren die zum Ein- und
Ausschalten benutzt werden (Leistungselektronik, z.B. Ansteuerung von elektrischen
Antrieben). Auch die gesamte Digitaltechnik basiert auf dem möglichst vollständigen Einund Ausschalten von Transistoren, die auf diese Weise die logischen Zustände ’0’ bzw. ’1’
darstellen.
u0
RC
R2
C1
Hochschule Bremerhaven --- IAE
Mit dem Großsignalverhalten wird der Transistor in seinem gesamten Kennlinienfeld
richtig beschrieben.
Lösungen: R1 = 452Ω , UDS = 5.54V.
9.5.2
E K. Müller
45
Elektronik und Prozessmesstechnik
Verstärker mit JFET
Transistorkenngrößen
Schaltungen mit Transistoren werden mit den gleichen Mitteln wie bei den passiven
Netzwerken analysiert. Hinzu kommen lediglich gesteuerte Spannungs- bzw. Stromquellen. Aufgrund der Nichtlinearität der Transistoren (Spannungen und Ströme sind nicht
proportional wie bei den Widerständen) unterscheidet man zwischen Großsignal- und
Kleinsignalverhalten.
10.2
u0
uC
Arbeitspunkt einer Transistorschaltung mit einem Kollektorwiderstand
Kleinsignalverhalten (Wechselstromverhalten)
Das Kleinsignalverhalten beschreibt den Transistor in der Nähe des Arbeitspunkts.
Entscheidend für das Verhalten sind die Steigungen der Kennlinien im Arbeitspunkt, also
die Ableitungen im Arbeitspunkt. Für kleine Abweichungen vom Arbeitspunkt ist der
Transistor wieder ein lineares Bauelement. Die Ausgangsgröße hat dann wieder die gleiche
Form wie die Eingangsgröße. Beispielsweise erhält man bei einer sinusförmigen
Eingangsspannung wieder eine sinusförmige Ausgangsspannung mit wesentlich größerer
Amplitude (linearer Verstärker).
E K. Müller
46
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
IC
IB
Bild 1.65:
E
Ein für den Entwurf wichtiger Faktor ist natürlich die Stromverstärkung
Messschaltung für einen NPN-Transistor
B=
Für einen Transistor in der Testschaltung nach Bild 1.65 gilt
UBE
(1.47)
I C = I S(T, U CE) e UT .
Der Kollektorstrom steigt also exponenziell mit der Basisspannung an. Der Strom IS ist
der (sehr kleine) Sperrstrom, der von der Temperatur T sowie in geringem Maße auch von
der Spannung UCE abhängt. Die differenzielle Abhängigkeit des Kollektorstrom von der
Basisspannung nennt man Steilheit
S :=
∂I C
∂U BE

(1.48)
.
UCE=const
Führt man die Differentiation aus, so erhält man
S=
I
I S UBE
e UT = C .
UT
UT
IC
,
IB
β :=
∂I C
∂I B


(1.53)
∂U BE
∂U
βU T
β
= ∂IBE = =
.
S
∂I B
IC
C
(1.54)
Fasst man die partiellen Ableitungen zusammen, so folgen die totalen Differenziale
.
(1.50)
dI B =
∂I B
∂I B
∂I B
dU +
dU ≈
dU = r 1 dU BE ,
∂U BE BE ∂U CE CE
∂U BE BE
BE
(1.55)
dI C =
∂I C
∂I C
dU +
dU = S dU BE + r 1 dU CE .
∂U BE BE ∂U CE CE
CE
(1.56)
U BE=const
Entsprechend ist ein differenzieller Eingangswiderstand definiert
∂U BE
∂I B
.
UCE=const
β
(1.49)
In Bild 1.64 ist dieser Wert das Verhältnis ∆U / ∆I. Der Widerstand nimmt mit steigendem
IC ab.
r BE :=

Bei Kenntnis der Stromverstärkung β lässt sich der differenzielle Eingangswiderstand
berechnen
Ein weiterer wesentlicher Parameter ist der differenzielle Ausgangswiderstand
∂U CE
∂I C
(1.52)
die strenggenommen vom Kollektorstrom abhängt. Diese sogenannte
statische
Stromverstärkung B unterscheidet sich etwas von der differenziellen Stromverstärkung
r BE :=
Zur Bestimmung der Steilheit ist also kein spezifisches Datenblatt erforderlich. Die
Temperaturspannung beträgt bei Raumtemperatur etwa UT = 26mV.
r CE :=
Hochschule Bremerhaven --- IAE
Ein- und Ausgangswiderstände müssen bekannt sein, wenn die zu entwerfende Schaltung
Bestandteil einer größeren Schaltung ist. Der Eingangswiderstand muss möglichst groß
sein, um einen vorangegangenen Schaltungsteil nicht zu stark zu belasten. Der
Ausgangswiderstand muss möglichst klein sein, damit die nachfolgende Schaltung die
Ausgangsspannung möglichst nicht verändert.
UCE
UBE
47
Das Verhalten der Basis-Emitter-Strecke unterscheidet sich nicht vom Verhalten einer
Diode.
C
B
Elektronik und Prozessmesstechnik
.
U CE=const
(1.51)
Für kleine Abweichungen vom Arbeitspunkt ist damit das Ersatzschaltbild 1.66 gültig.
E K. Müller
48
Elektronik und Prozessmesstechnik
spannungsgesteuerte
Stromquelle
iB
Hochschule Bremerhaven --- IAE
E K. Müller
49
Elektronik und Prozessmesstechnik
RB
iC
B
U0
C
uBE
rBE
S uBE
rCE
uCE
U1
Hochschule Bremerhaven --- IAE
RE
U2
E
Bild 1.66:
Ersatzschaltbild des Bipolartransistors (=Giacoletto-Ersatzschaltbild)
Beachten Sie die Kleinbuchstaben für Spannungen und Ströme (=Änderungen vom
Arbeitspunkt!).
11
Transistorgrundschaltungen
Mit den Kenngrößen aus Abschnitt 10 lassen sich die Standardschaltungen mit Transistoren
systematisch entwerfen. Man unterscheidet Basis-, Kollektor- und Emitterschaltungen.
U0
RC
RE
U1
Bild 1.67:
U2
RC
Emitter-Schaltung
Die Schaltungsvarianten werden für folgende Einsatzgebiete verwendet:
S
Basisschaltung: Hochfrequenzverstärker für Frequenzen > 200MHz. Die guten
Hochfrequenzeigenschaften sind die einzigen Vorteile der Schaltung. Das Einsatzgebiet ist die Nachrichtentechnik. Die Schaltungsvariante wird hier nicht weiter verfolgt.
S
Emitterschaltung: Diese Schaltung wird zur Verstärkung von Signalen eingesetzt.
Einsatzgebiete sind Messtechnik und NF-Technik, also z.B. Audioverstärker.
S
Kollektorschaltung (auch Emitterfolger genannt): Diese Schaltung ermöglicht eine
Impedanzwandlung, d.h. bei sehr hohem Eingangswiderstand zeigt die Schaltung einen
niedrigen Ausgangswiderstand. Für die Verstärkung gilt A < 1.
Kleinsignal-Ersatzschaltbilder
Bei Wechselstrom müssen alle konstanten Potenziale zusammengelegt werden und alle
Kondensatoren werden durchlässig. Dies folgt aus einer Betrachtung der Änderungen um
einen konstanten Arbeitspunkt.
U0
11.1.1
RB
Bild 1.68:
Kollektor-Schaltung
Die Namen der Schaltungen leiten sich aus dem Anschluss des Transistors her, der das
gemeinsame Bezugspotenzial zwischen Eingang und Ausgang bildet. Bei der
Kollektorschaltung (Bild 1.69) ist dies nicht unmittelbar ersichtlich. Für das
Kleinsignalverhalten besitzen Spannungsquellen (in diesem Fall U0) keinen differenziellen
Widerstand (Ri = 0Ω). Dies wird auch dadurch verständlich, dass sich ideale
Spannungsquellen als Kondensatoren mit unendlicher Kapazität auffassen lassen.
11.1
Basis-Schaltung
U1
Bild 1.69:
U2
Bestimmung von differenziellen Widerständen
Der differenzielle Widerstand ist der Widerstand, der sich aufgrund der Änderung einer
Spannung oder eines Stromes ergibt. Dieser Widerstand kann bestimmt werden, indem alle
Spannungsquellen mit konstantem Potenzial mit der Masse verbunden werden.
11.1.2
Beispiel
Für folgende Schaltung soll der differenzielle Widerstand bestimmt werden, der für
Änderungen der Spannung Ux wirksam ist.
E K. Müller
50
Elektronik und Prozessmesstechnik
R1
E K. Müller
Hochschule Bremerhaven --- IAE
I1
∆Ix
U0
Bild 5.1:
R2
Hochschule Bremerhaven --- IAE
heißt differenzieller Widerstand, der die Änderung der Stroms bezogen auf die Spannung
angibt. Diesen Widerstand kann man leichter bestimmen, wenn man das Kleinsignal-Ersatzschaltbild verwendet (die konstante Spannung U0 wird durch einen Kurzschluss
ersetzt).
Ix
Ux
51
Elektronik und Prozessmesstechnik
I2
∆I1
R2
∆Ux
∆I2
R1
Schaltungsbeispiel
Bild 5.2:
Aus der linken Masche folgt
I2 =
Ux
.
R2
(5.1)
⇒ I1 =
U0 − Ux
.
R1
(5.2)
Der Strom Ix ergibt sich aus der Knotengleichung
(5.3)
Ix = I2 − I1 .
Hier wird deutlich, dass der differenzielle Widerstand rx aus der Parallelschaltung von R1
und R2 gebildet wird.
HINWEIS: Anstelle der Größen ∆Ux , ∆Ix usw. verwendet man Kleinbuchstaben (ux , ix ).
Mit Hilfe der äußeren Masche lässt sich der Strom I1 ausrechnen
U x − U 0 + R 1I 1 = 0 ,
Ersatzschaltbild für Kleinsignale (Änderungen)
11.2
Emitterschaltung
Die Emitterschaltung kann analysiert werden, wenn der Transistor in Bild 1.68 durch das
Transistor-Ersatzschaltbild 1.66 (Giacoletto) ausgetauscht wird.
U0
Nun kann man die Ströme I1 und I2 ersetzen und erhält
Ix =


U
Ux U0 − Ux
−
= Ux 1 + 1 − 0
R2
R1
R1
R2 R1
(5.4)
RB
oder auch
B
R + R2 U0
−
.
Ix = U x 1
R 1R 2
R1
(5.5)
U1
Bei einer Änderung der Spannung Ux änder sich der Strom Ix gemäß
R + R2
∂I x
= 1
:= r1 .
x
∂U x
R 1R 2
R 1R 2
R1 + R2
C
rBE
S UBE
rCE
UCE = U2
E
(5.6)
Bild 1.70:
Emitter-Schaltung mit Transistor-Ersatzschaltbild (Giacoletto)
Sofern man nur Signaländerungen betrachtet, können alle Potentiale, die
Gleichspannung führen, zusammengeschaltet werden.
Der Widerstand
rx =
UBE
IC
RC
IB
(5.7)
Man erhält aus Bild 1.70 das folgende Ersatzschaltbild.
E K. Müller
52
Elektronik und Prozessmesstechnik
iB
RB
iC
B
u1
uBE
E K. Müller
Hochschule Bremerhaven --- IAE
C
rBE
Hochschule Bremerhaven --- IAE
Damit folgt dann die Spannungs-Verstärkung
u
A := u 2 = − SR C = − 76.9 mA 5kΩ = − 384.6 .
V
1
rCE
S uBE
53
Elektronik und Prozessmesstechnik
RC
uCE = u2
(1.60)
Das negative Vorzeichen bedeutet, dass das Ausgangssignal
Eingangssignal verläuft.
gegenphasig
zum
E
Bild 1.71:
Emitter-Schaltung mit Transistor-Ersatzschaltbild (Giacoletto) für Kleinsignalverhalten
Wann immer möglich vereinfacht man die Schaltung soweit als möglich, indem man die
Auswirkungen sehr großer neben sehr kleinen Widerständen analysiert. Gewöhnlich wählt
man RB ≪ rBE und es gilt fast immer rCE ≫ RC . Unter Anwendung des KIS-Prinzips
erhält man folgende sinnvolle Vereinfachung.
12
Kollektorschaltung
Bei der Kollektorschaltung (s. Bild 1.69) bildet --- wie der Name schon sagt --- der Kollektor
das gemeinsame Bezugspotenzial für Eingang und Ausgang.
VCC = U0
KIS = keep it simple (Grundprinzip der Ingenieure).
R1
Falls diese Vereinfachungen nicht statthaft sind, muss die kompliziertere Schaltung
gerechnet werden. Es kann die vollständige Schaltung natürlich auch simuliert werden.
iB
iC
B
u1 = uBE
C
rBE
S uBE
RC
uCE = u2
U1
R2
RE
U2
E
Bild 1.72:
Vereinfachte Emitter-Schaltung
Bild 1.73:
Man liest nun aus Bild 1.72 die einfache Beziehung
u 2 = u CE = − i CR C = − S u BER C = − SR C u 1
(1.57)
ab. Damit lautet die Spannungs-Verstärkung (Verhältnis der Spannungen von Ausgang zu
Eingang)
u
A := u 2 = − SR C .
1
(1.58)
Beispiel: IC = 2mA, RC = 6,8kΩ.
Zunächst muss die Steilheit bestimmt werden (1.49)
S = 2mA = 76.9 mA .
V
26mV
(1.59)
Typische Kollektor-Schaltung
Die Kondensatoren an den Ein- und Ausgängen sperren Gleichsignale und stellen für
Wechselströme praktisch keine Widerstand dar. Sie lassen also die Nutzsignale
(Kleinsignalverhalten) ungehindert passieren, beeinflussen andererseits die Arbeitspunkteinstellung (Großsignalverhalten) aber nicht.
Für die Einstellung des Arbeitspunkts wirken die Kondensatoren also wie ein unendlich
großer Widerstand, d.h. sie können zur Berechnung des Arbeitspunkts entfallen
(Bild 1.74).
E K. Müller
54
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
VCC = U0
55
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Aus dem Schaltbild 1.75 liest man ab
(1.63)
U 0 = U 1 + U 2 = R 1I 1 + R 2I 2 .
IC
R1
Die untere Masche liefert
U E + U BE − U 2 = I B + B I BR E + U BE − R 2I 2 = 0 .
IB
Die Stromsumme am rechten Knoten (IE = IB +B IB ) wurde bereits benutzt. Weiterhin
folgt aus dem linken Knoten
UCE
UBE
(1.65)
I1 = I2 + IB .
R2
RE
(1.64)
Aus den drei Gleichungen (1.63)---(1.65) folgen die drei Ströme I1, I2 sowie IB . Es
interessiert jedoch nur IB bzw. IC zur Bestimmung des Arbeitspunkts.
UE
Einsetzen von (1.65) in (1.63) liefert
Bild 1.74:
U 0 = R 1I2 + I B + R 2I 2
Bestimmung des Arbeitspunkts bei der Kollektorschaltung
bzw.
Die Spannung zwischen Basis und Emitter kann als konstant
(1.61)
U BE ≈ 0.6V
angenommen werden. Der Kollektorstrom ist um den Wert der Stromverstärkung größer
als der Basisstrom
(1.62)
IC = B IB .
Man erhält folgende Schaltung, mit der eine Arbeitspunktbestimmung möglich ist.
U0
U1, I1
R1
IB
I2 =
U 0 − R 1I B
.
R1 + R2
(1.67)
Die Gleichungen (1.64) und (1.67) bilden nun ein Gleichungssystem mit den zwei
Unbekannten I2 und IB , aus denen sich IB berechnen lässt. Es folgt nach Auflösen nach
dem Basisstrom
IB =
R2
R 1+R 2 U 0
− U BE
(1.68)
.
R R
1 2
(1 + B) R E + R +R
1
U0
(1.66)
2
bzw. für den gesuchten Kollektorstrom
IC = B IB
IC = B IB = B
UBE
R2
R 1+R 2 U 0
− U BE
1
2
Mit B ≫ 1 folgt dann einfach aufgrund von (1 + B)R E ≫
U2, I2
Bild 1.75:
R2
RE
UE
Bestimmung des Arbeitspunkts bei der Kollektorschaltung
IC ≈
R2
R 1+R 2 U 0
− U BE
RE
.
(1.69)
.
R R
1 2
(1 + B) R E + R +R
R 1R 2
,
R1 + R2
B ≈1
1+B
(1.70)
Aufgrund der hohen Stromverstärlung B des Transistors folgt der Kollektorstrom aus dem
Spannungsteiler auf der Basisseite (durch R1 und R2), dem Spannungsabfall an der Basis
und dem Emitterwiderstand RE . Diese Beziehung (1.70) gilt für jeden Transistor, der über
eine hinreichend große Stromverstärkung verfügt.
E K. Müller
56
Elektronik und Prozessmesstechnik
12.1
E K. Müller
Hochschule Bremerhaven --- IAE
Kleinsignal-Ersatzschaltbild mit Transistor
iC
rBE
uBE
u1
R1
Bild 1.76:
S uBE
1
iE
u2
(1.71)
u 1 = u BE + R Ei E .
Der Strom iE ist die Summe aus Basisstrom iB und Kollektorstrom iC

u BE
r BE + S u BE .
(1.72)

 

u
SR
S BE + S u BE = 1 + E + SR E u BE
β
β
(1.73)
u1
1+
SR E
+ SR E
β
(1.74)
.
Die Ausgangsspannung ist
 

SRβ
E
SR E
≈1.
1 + SR E
(1.77)
Man ist stets bestrebt den Eingangswiderstand eines Schaltungsteils möglichst groß zu
machen, um die vorangehende Stufe möglichste wenig zu belasten. Ist auf der anderen Seite
der Ausgangswiderstand sehr gering, so führt eine Belastung des Ausgangs wenig zu einer
Änderung der Spannung.
Zunächst erkennt man, dass am Eingangswiderstand die Parallelschaltung aus R1 und R2
beteiligt ist. Im Interesse eines großen Eingangswiderstands sollte man also diese
Widerstände möglichst groß wählen. Weiterhin ist der Widerstand u1 / iB zu bestimmen.
Hier ist es jedoch leichter, den Leitwert
di B
1
r e = du
(1.78)
1
u
S u BE
.
i B = r BE =
β
BE
(1.79)
u
i B = r BE =
BE
S
β
1+
SR E
+ SR E
β
(1.80)
u1
und daraus

u
R
u 2 = R E iE = R E r BE + Su BE = r E + SR E u BE .
BE
BE
=
≈
Mit (1.74) erhält man
bzw.
u BE =
SR E
+ SR E
β
SR E
1 + β + SR E
zu ermitteln. Der Basisstrom ist
Aus (1.54) folgt durch Ersetzen von rBE
u 1 = u BE + R E
(1.76)
u1 .
Die Verstärkung ist also unabhängig von den Transistordaten etwa 1 (bzw. ein wenig kleiner
als 1). Worin liegt nun der Sinn der Kollektorschaltung? Die Antwort folgt aus der
Bestimmung der Ein- und Ausgangswiderstände der Schaltung.
Die Widerstände R1 und R2 wirken als Parallelschaltung und verringern den
Eingangswiderstand. Auf die Spannungsverstärkung A haben sie keinen Einfluss. Durch
Spannungsumlauf in der linken Masche erhält man

SR E
+ SR E
β
SR E
1 + β + SR E
u
A = u2 =
Wechselstrom-ESB der Kollektor-Schaltung
u 1 = u BE + R E
u2 =
Daraus erhält man die Verstärkung
R2
RE
Hochschule Bremerhaven --- IAE
Setzt man nun (1.74) in (1.75) ein, d.h. man ersetzt uBE , so folgt
Für den Transistor wird wieder das Giacoletto-Ersatzschaltbild verwendet. Damit entsteht
Bild 1.76.
iB
57
Elektronik und Prozessmesstechnik

+ SR E u BE .
dI B
1
r e = dU =
1
(1.75)
S
β
1+
SR E
β
+ SR E
Der Eingangswiderstand ist damit
≈
S
β
1 + SR E
≈
S
β
SR E
= 1 .
βR E
(1.81)
E K. Müller
58
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
(1.82)
r e ≈ βR E .
Er liegt damit gewöhnlich mit Bereich von mehreren 100 kΩ bis MΩ, was für
messtechnische Zwecke einen erstrebenswerten Wert darstellt. Der tatsächliche
Eingangswiderstand vermindert sich jedoch um die Parallelschaltung von R1 und R2.
Elektronik und Prozessmesstechnik
59
Hochschule Bremerhaven --- IAE
Der Ausgangswiderstand in der Kollektorschaltung ist somit vom Transistortyp
unabhängig. Bei einem Kollektorstrom von 5mA (Arbeitspunkt) folgt für den
Ausgangswiderstand der sehr kleine Wert
ra ≈ 1 =
S
1 = 26mV = 5.2Ω .
5mA
(1.88)
5mA
26mV
Der differenzielle Ausgangswiderstand ist
ra =
∂u 2
.
∂i 2
(1.83)
Bestimmen lässt sich der Ausgangswiderstand als Verhältnis der Ausgangsspannung U2
zum Ausgangsstrom i2
bei der Eingangsspannung
u1 = 0.
Man zeichnet
zweckmäßigerweise Bild 1.76 etwas um.
i2
uBE
Bild 1.77:
rBE RE
iE
S uBE
13
Differenzverstärker
Ein großer Teil der Elektronikschaltungen für messtechnische Aufgaben besteht aus
sogenannten Operationsverstärkern, die als integrierte Schaltung (IC) aus mehreren
elektronischen Bauelementen bestehen. Die einfachste Form ist der sogenannte
Differenzverstärker.
u2
RC
RC
Wechselstrom-ESB der Kollektor-Schaltung zur Bestimmung des Ausgangswiderstands
uA1
Man liest unmittelbar aus Bild 1.77 den Ausgangsstrom i2 ab
u
u
i 2 = r 2 + 2 − Su BE .
RE
BE
uA2
uE 1
(1.84)
RE
uE 2
Weiterhin sieht man sofort, dass uBE = ---u2 gilt. Somit erhält man

 

u
u
i 2 = r 2 + 2 + Su 2 = r 1 + 1 + S u 2 = S + 1 + S u2 .
RE
RE
β RE
BE
BE
(1.85)
Der Ausgangsleitwert folgt zu
∂I 2
SR E + β + βSR E
S
1
1
r a = ∂U = β + R + S =
βR E
2
E
βR E
RE
RE
R
= SR
≈
≈ E =1 .
E
SR E
S
1 + SR E
SR E + β + βSR E
+ 1 + SR
β
E
Differenzverstärker mit zwei Transistoren
(1.86)
Der Differenzverstärker besitzt zwei Eingänge (uE1, uE2) und die zwei Ausgänge
(uA 1, uA 2). Gewöhnlich wird aber nur einer der Ausgänge verwendet. Die Transistoren sind
über den gemeinsamen Emitterwiderstand RE gekoppelt.
(1.87)
Die Analyse der Schaltung ist recht aufwändig. Eine relativ einfache Lösung erhält man,
wenn man die Eingangsspannungen in Gleichtakt- und Gegentaktsignal zerlegt und die
Verstärkung für beide Anregungen berechnet. Das Gleichtaktsignal ist die gleichförmige
Erhöhung oder Verminderung der Spannungen uE1 und uE2.
und damit
ra =
Bild 1.78:
u G := u E1 + u E2 .
(1.89)
E K. Müller
60
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
Entsprechend gilt für das Gegentaktsignal
(1.90)
u D := u E1 − u E2 .
Löst man das Gleichungssystem (1.89), (1.90) nach uE1 und uE2 auf, so erhält man
u E1 = 1 u G + u D ,
2
(1.91)
u E2 = 1 u G − u D .
2
(1.92)
Elektronik und Prozessmesstechnik
61
Hochschule Bremerhaven --- IAE
Operationsverstärker (OPs) werden als integrierte Schaltungen (ICs) ausgeführt. Das
Innenleben eines Operationsverstärker-ICs sei am Beispiel des TL081 von Texas
Instruments gezeigt. Man erkennt, dass die integrierten Schaltungen recht komplex
ausfallen.
Die Ausgangsspannung UA 2 folgt mit den Vereinfachungen
SR E ≫ 1 ,
u A2 ≈
SR C ≫ 1 ,
1+β
≈1
β
(1.93)
RC
2SR C u D − u G .
4R E
(1.94)
Die Verstärkung für das Gegentaktsignal ist also deutlich größer als die Verstärkung für
Gleichsignale; dies ist eine Folge der Kopplung über den gemeinsamen Emitterwiderstand.
Diese Eigenschaft ist in höchstem Maße erwünscht. Dieses Verhalten wird gezielt optimiert
in integrierten Schaltungen, die Operationsverstärker henannt werden.
14
Operationsverstärker
Bild 1.80:
Operationsverstärker sind sehr wichtige Bauelemente für die elektronische Messtechnik.
Verstärkung, Impedanzwandlung und Filterung werden heute überwiegend mit
Operationsverstärkern verwirklicht.
In elektronischen Schaltungen werden Operationsverstärker durch ein Dreieck dargestellt.
Die Eingänge werden als nicht-invertierender Eingang (+) sowie invertierender
Eingang (---) gekennzeichnet. Den Ausgang bildet die Spitze des Dreiecks.
invertierender Eingang
---
nicht-invertierender Eingang
+
Bild 1.79:
Ausgang
Symbol des Operationsverstärkers
Das Symbol darf auch noch andere Anschlüsse enthalten (z.B. Versorgungsspannung,
Frequenzgang- oder Offset-Kompensation)
TL081 BiFETR Operationsverstäker (Feldeffekt- und Bipolartransistoren)
Operationsverstärker-ICs enthalten einen, zwei oder vier Operationsverstärker.
E K. Müller
Elektronik und Prozessmesstechnik
Bild 1.81:
62
Hochschule Bremerhaven --- IAE
E K. Müller
Elektronik und Prozessmesstechnik
63
Anschlussbelegungen gebräuchlicher Operationsverstärker-ICs
Als Beispiel für einen modernen Operationsverstärker sind die Daten des LT1013/LT1014
von Linear Technology aufgeführt.
Bild 1.82:
Anschlüsse des LT1013 (Pinout Diagram)
Hochschule Bremerhaven --- IAE
E K. Müller
Elektronik und Prozessmesstechnik
64
Hochschule Bremerhaven --- IAE
E K. Müller
Elektronik und Prozessmesstechnik
65
Hochschule Bremerhaven --- IAE
Wie man an den Daten des LT1014 erkennt, ist ein moderner Operationsverstärker ein fast
ideales Bauelement. Zur Berechnung von Schaltungen kann man deshalb von einem
idealen Operationsverstärker ausgehen, ohne dass die berechneten Eigenschaften von den
der realen Schaltung nennenswert abweichen.
iN
iP
uN
--+
uP
Bild 1.85:
uA
Definition der Spannungen und Ströme
Ein idealer Operationsverstärker ist durch folgende Eigenschaften gekennzeichnet:
Bild 1.83:
Technische Daten des LT1013/LT1014
S
Unendliche Verstärkung für Gegentaktanregung, d.h. für uD = uP - uN . Natürlich
kann kein realer Operationsverstärker eine unendliche Verstärkung erreichen. Die
Verstärkung für OPs liegt in der Größenordnung von V ≈ 106.
S
Verstärkung null für Gleichtaktsignale uG = uP + uN . Werden also uP und uN gleich
erhöht oder erniedrigt, so ändert sich die Ausgangsspannung nicht.
S
Eingangswiderstände RE → ∞, d.h. die Eingangsströme iP und iN sind null.
S
Ausgangswiderstand RA = 0, d.h. die Ausgangsspannung hängt nicht von der
nachfolgenden Schaltung ab. Die Ausgangsspannung wird somit vom OP “eingeprägt”.
S
Die Offset-Spannung ist null. Unter Offset-Spannung versteht man die Spannung uD ,
für die die Ausgangsspannung null wird. Bei realen OPs liegt diese Spannung im Bereich
von Mikrovolt.
14.1
Prinzip von OP-Schaltungen
Bereits in den 40er Jahren wurde entdeckt, dass mit dem Prinzip der Gegenkopplung die
Eigenschaften von Verstärkern sehr verbessert werden können. Dieses Prinzip macht man
sich bei OP-Schaltungen zunutze. Die hohe Verstärkung für Gegentaktanregung wird
durch Gegenkopplung auf das benötigte Maß reduziert. Die Schaltung wird durch
Gegenkopplung weitgehend unabhängig von der Verstärkung des OPs.
Die Eigenschaften der Schaltung hängen nur von der äußeren Beschaltung ab.
Bild 1.84:
Interner Aufbau des Operationsverstärkers LT1013/LT1014
Eine typische Schaltung zeigt Bild 1.86. Der Ausgang wird über den Widerstand R2 auf den
negativen Eingang zurückgeführt (deshalb die Bezeichnung Gegenkopplung).
E K. Müller
66
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
R2
i1
R1
uD
u1
Bild 1.86:
--+
Hochschule Bremerhaven --- IAE
Das Verhältnis von Ausgangs- zu Eingangsspannung wird damit
R2
u2
u1 = − R
(1.102)
1
i2
und hängt folglich nur von der äußeren Beschaltung ab. Diese Beziehung gilt auch für
beliebige komplexe Impedanzen.
u2
Z2
I1
Operationsverstärker in Gegenkopplung
Für die Schaltung gilt
Z1
U1
(1.95)
u2 = V uD
67
Elektronik und Prozessmesstechnik
ud
--+
i2
U2
oder umgekehrt
uD =
u2
.
V
(1.96)
Für unendlich angenommene Verstärkung gilt dann
u D = lim
V→∞
u2
=0,
V
(1.97)
da natürlich die Ausgangsspannung u2 endliche Werte annimmt. Damit liegt der negative
Eingang des OPs (wie auch der positive Eingang) auf Massepotenzial.
Dieser Effekt wird virtuelle Masse genannt.
Bild 1.87:
Operationsverstärker in Gegenkopplung mit komplexen Impedanzen und
Spannungszeigern
Das Übertragungsverhalten
Z
U1
= F := − 2
U2
Z1
(1.103)
ist dann der Frequenzgang F.
Frequenzgang F(jw) = ---Z2 / Z1
Damit folgt der Eingangsstrom
i1 =
u1
.
R1
(1.98)
Da der OP einen unendlichen Eingangswiderstand aufweist, fließt dieser Strom auch
durch R2, d.h. es muss gelten
(1.99)
i2 = i1 .
Aufgrund der virtuellen Masse am positiven Anschluss folgt der Zusammenhang zwischen
der Ausgangsspannung u2 und dem Strom i2
(1.100)
u 2 = − R 2i 2 .
Setzt man (1.99) und (1.98) in (1.100) ein, so folgt
u 2 = − R 2i 1 = −
R2
u .
R1 1
(1.101)
Schaltungen mit Operationsverstärkern nennt man aktive Filter.
14.2 Serienschaltung von Operationsverstärkern
Operationsverstärker besitzen einen sehr kleinen Ausgangswiderstand, d.h. die
Ausgangsspannung hängt nicht von der nachfolgenden Beschaltung ab. Jede Schaltung mit
einem Operationsverstärker ist folglich unabhängig von vorgegangenen oder nachfolgenden Stufe.
E K. Müller
68
Elektronik und Prozessmesstechnik
Z2
I1
69
Elektronik und Prozessmesstechnik
Seine Realisierung als aktives Filter ist in Bild 1.89 gezeigt.
Z3
---
ud
+
Hochschule Bremerhaven --- IAE
Z4
Z1
U1
U2
F1(jω)
Bild 1.88:
E K. Müller
Hochschule Bremerhaven --- IAE
ud
C
--+
R2
R1
U3
Z2
--U1
F2(jω)
+
U2
Serienschaltung von Operationsverstärkern
Für die in Bild 1.88 gezeigte Schaltung gilt
Z
F 1(jω) = − 2 ,
Z1
Z
F 2(jω) = − 4 .
Z3
Bild 1.89:
(1.104)
Zunächst berechnet man
Aufgrund von
U 2 = F 1U 1
(1.105)
U 3 = F 2U 2
(1.106)
U 3 = F 2U 2 = F 2F 1U 1 .
(1.107)
sowie
Tiefpassfilter 1. Ordnung
Z2 =
1
R 2 jωC
R2
1 + jωR2C
(1.109)
Z2
R
1
=− 2
R1
R 1 1 + jωR 2C
(1.110)
1
R 2 + jωC
=
Der Frequenzgang ist dann
F(jω) = −
folgt
Eine Verstärkung von “1” erhält man für R2 = R1. Sollte die negative Verstärkung stören,
so kann ein Verstärker mit der Verstärkung ---1 nach- oder vorgeschaltet werden.
Der gesamte Frequenzgang ist somit einfach das Produkt aus den einzelnen
Frequenzgängen. Bei passiven Filtern gilt dieser einfache Zusammenhang natürlich nicht.
R1
R1
14.3 Tiefpassfilter 1. Ordnung
Filter unterscheidet man anhand ihrer Ordnung. Je größer dir Ordnung, desto größer ist
ihre Wirksamkeit. Allerdings steigt der Realisierungsaufwand. Die Ordnung n gibt an, wie
groß die Änderung der Verstärkung bezogen auf die Frequenzänderung ist. Dieses
Verhalten tritt natürlich erst jenseits der Grenzfrequenz auf. Falls also die Verstärkung sich
bei einer Verdoppelung der Frequenz halbiert, spricht man von einem Filter 1. Ordnung.
Der Frequenzgang lautet
F(jω) =
1
.
1 + jωRC
(1.108)
U1
Bild 1.90:
ud
--+
U2
Schaltung mit der Verstärkung “---1”
Filter höherer Ordnung kann man durch Hintereinanderschaltung mehrerer Filter
1. Ordnung erzeugen.
E K. Müller
70
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
E K. Müller
14.4 Hochpassfilter 1. Ordnung
+
Ein Hochpassfilter könnte man durch den Austausch des Kondensator in Bild 1.89 gegen
eine Induktivität erzeugen. Allerdings sind Induktivitäten um Größenordnungen teurer als
Kondensatoren. Deshalb verwendet man auch in Hochpassfiltern nur Widerstände und
Kondensatoren. Die Realisierung eines Hochpassfilters 1. Ordnung ist in Bild 1.91 gezeigt.
Z1
C
ud
U1
--+
uE 1
Bild 1.92:
R2
R1
71
Elektronik und Prozessmesstechnik
uE 2
---
Hochschule Bremerhaven --- IAE
*
uA
Komparator
Die Eingänge des Komparators sind analoge Signale.
Die Eingangssignale können beliebige Werte (im erlaubten Spannungsbereich) annehmen.
U2
Der Ausgang des Komparators ist ein digitales Signal.
Bild 1.91:
Hochpassfilter 1. Ordnung
Der Ausgang nimmt nur noch zwei Werte an, die folgende Bedeutung haben
Zunächst wird wieder Z1 ausgerechnet
1 + jωR1C
.
Z1 = R 1 + 1 =
jωC
jωC
u E1 > u E2 ,
(1.111)
Der Frequenzgang lautet damit
F=−
jωR 1C
R2
jωR 2C
R
=−
=− 2
.
Z1
R 1 1 + jωR 1C
1 + jωR 1C
(1.113)
u E1 ≤ u E2 .
Die Ausgangsspannung nimmt abhängig von der z der Eingangssignale nur noch zwei
Werte an
(1.112)
+ U A,max
uA = 
− U A,max

Für R1 = R2 erhält man einen Betrag der Verstärkung bei hohen Frequenzen von 1.
für uE1 > u E2
für uE1 ≤ u E2
(1.114)
.
14.5 Bandpassfilter und Bandsperren
Bei einem Komparator-IC (z.B. L331, LM393, LM339) ist der Ausgang kompatibel zu
digitalen ICs (TTL/CMOS). Diese Art von ICs nennt man auch Interface-ICs.
Bandpassfilter sind Filter, die einen bestimmten Frequenzbereich übertragen und die
Frequenzen außerhalb dieses Bereiches unterdrücken.
Mit einem Operationsverstärker lassen sich leicht Komparatoren erzeugen.
Bei einer Bandsperre wird ein Frequenzbereich ausgespart (unterdrückt). Die Frequenzen
außerhalb dieses Bereiches sollen möglichste ungehindert das Filter passieren.
+
Bandsperren und Bandfilter lassen sich durch Kombination von Hochpass- und
Tiefpassfiltern realisieren. Beispielsweise ergibt die Serienschaltung einer Hochpassfilters
mit einem Tiefpassfilter --- bei entsprechender Wahl der Grenzfrequenzen --- einen
Bandpass.
15
Komparator
Häufig muss man Spannungspegel auf bestimmte Grenzwerte hin überprüfen. Diese
Aufgabe übernehmen Komparatoren. Der Komparator bildet die Schnittstelle zwischen
Analog- und Digitaltechnik.
uE 1
Bild 1.93:
--uE 2
uA
Komparator mit Operationsverstärker
Operationsverstärker arbeiten schneller, wenn die Spannung zwischen positivem und
negativem Anschluss möglichst gering gehalten wird. Aufgrund der hohen Verstärkung
genügen auch kleine Spannungen. Die Spannung lässt sich mit zwei antiparallelen Dioden
auf die Werte ±0,7V beschränken.
E K. Müller
Elektronik und Prozessmesstechnik
72
Hochschule Bremerhaven --- IAE
R
E K. Müller
Elektronik und Prozessmesstechnik
73
Hochschule Bremerhaven --- IAE
Vin
5V
uE 1
R
uE 2
Bild 1.94:
+
---
2,9V
2,5V
2,1V
uA
Komparator mit Begrenzung der Eingangsspannung
Häufig muss die Ausgangsspannung auf bestimmte Werte beschränkt werden. Diese
Maßnahme erhöht außerdem ebenfalls die Geschwindigkeit des Komparators.
R
uE 1
R
uE 2
0V
t
Vout
High
Low
--+
Komparator
uA = ±Uz
t
Vout
High
Bild 1.95:
Komparator mit Begrenzung der Ausgangsspannung
Die Ausgangsspannung ist nun auf den Wert der Spannung der Z-Dioden + 0,7V
beschränkt.
Low
t
Bild 1.96:
15.1
Schmitt-Trigger
Inverter
Schmitt-Trigger
Jeder praktisch eingesetzte Komparator verfügt über eine Hysterese, d.h. die
Schaltschwellen für die Umschaltung zur positiven oder negativen Ausgangsspannung
fallen nicht zusammen.
Schmitt-Trigger
Anhand von Bild 1.96 kann man die Wirkungsweise des Schmitt-Triggers erkennen. Ein
gestörtes Eingangssignal (entsteht beispielsweise durch die Antennenwirkung einer
Leitung) kann nun eindeutig mit einer Spannung (in diesem Fall 2,5V) verglichen werden,
ohne dass sich die Störungen auf das Ausgangssignal auswirken.
Der Komparator verwendet den positiven Anschluss. Der Ausgang ist ebenfalls auf den
positiven Anschluss zurückgekoppelt (= Mitkopplung). Durch die Mitkopplung kann der
Ausgang nur jeweils bei der positiven oder der negativen Maximalspannung liegen. Die
Umschaltung zwischen beiden Spannungen wird durch die Eingangsspannung bewirkt.
E K. Müller
74
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
R2
i
ux = u1 −
+
R1
R2
R1
u − u 2 =
u +
u .
R1 + R2 1
R 1 + R 2 1 R 1 + R2 2
(2.5)
Der Nulldurchgang von ux erfolgt bei
---
ux
Hochschule Bremerhaven --- IAE
Nun kann der Strom durch (2.2) ersetzt werden und man erhält
R1
u1
75
Elektronik und Prozessmesstechnik
u2
u1 = −
R1
u .
R2 2
(2.6)
Den Zusammenhang zeigt das Bild 1.99.
Bild 1.97:
Schmitt-Trigger mit Operationsverstärker
u2
u20
Da der negative Anschluss mit Masse verbunden ist, erfolgt die Umschaltung immer dann,
wenn der positive Anschluss die Polarität wechselt (also von + nach --- oder umgekehrt).
Bei angenommenem idealen OPs fließ kein Strom in den OP hinein. Damit vereinfacht sich
die Bestimmung der Spannung ux (Spannung am positiven Anschluss des OP, s. Bild 1.97).
Damit kann zur Berechnung der Spannung ux der OP weggelassen werden.
u1
R2
i
R
− 1 u 20
R2
R1
Bild 1.99:
+
u1
Bild 1.98:
ux
---
15.2
Der Maschenumlauf (außen) liefert
(2.1)
Auflösen nach dem Strom führt auf
i=
u1 − u2
.
R1 + R2
---u20
Ein- und Ausgangsspannung des Komparators
Der Zusammenhang in Bild 1.99 wird Hysterese genannt. Der Umschaltpunkt hängt von
der Vorgeschichte ab.
u2
Schaltung zur Berechnung der Spannung ux
u 1 − u 2 − R 1 + R 2 i = 0 .
R1
u
R 2 20
(2.2)
Die linke Maschengleichung lautet
u 1 − u x − R 1i = 0
(2.3)
u x = u 1 − R 1i .
(2.4)
bzw.
Fensterkomparator (Fensterdiskriminator)
Der Fensterkomparator erkennt, ob eine Spannung in einem bestimmten Spannungsbereich (d.h. Fenster) liegt. Hierzu werden zwei Operationsverstärker und ein sogenanntes
UND-Gatter benötigt. Das UND-Gatter gehört in den Bereich Digitalschaltungen, die
später ausführlich behandelt werden.
E K. Müller
76
Elektronik und Prozessmesstechnik
+
u2
---
Hochschule Bremerhaven --- IAE
E K. Müller
Elektronik und Prozessmesstechnik
+
---
Hochschule Bremerhaven --- IAE
uE
*
X1
U2
&
uE
77
U1
y
*
X0
u1
t
x0
High
Low
Bild 1.100: Fensterkomparator
t
x1
Die Funktion soll anhand einer rampenförmigen Änderung der Spannung uE erläutert
werden.
High
Low
t
y
High
Low
t
Bild 1.101: Fenster-Diskrimiator
Man erkennt, dass das (digitale) Ausgangssignal y genau dann den logischen Wert ’1’
annimmt, wenn das Eingangssignal uE sich innerhalb der Schranken U1 und U2 befindet,
d.h. es gilt
y=
16

′1′
′0′
für U1 ≤ u E < U 2
.
sonst
(1.115)
Operationsverstärker-Schaltungstechnik
Operationsverstärker ermöglichen den kompakten Aufbau von komplexen analogen
Schaltungen. Moderne Operationsverstärker besitzen eine extrem hohe Differenzverstärkung, praktisch keine messbare Offsetspannung sowie einen fast unendlich hohen
E K. Müller
78
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
E K. Müller
i13
Eingangswiderstand. Evtl. ist hier bei Massenprodukten, bei denen Stückkosten eine große
Rolle spielen, ein Kompromiss aus elektrischen Eigenschaften und Preis zu schließen.
Hochwertige OPs kosten ca. 7€ / Stück.
uE 3
Im Bereich der Messtechnik verwendet man fast immer hochwertige OPs. Die
Schaltungseigenschaften hängen dann nur noch von der äußeren Beschaltung ab.
Negierer
Hochschule Bremerhaven --- IAE
R13
uE 2
R2
R12
i12
Schaltungen mit Operationsverstärkern dienen der analogen Signalverarbeitung. Um
beliebige Funktionen verwirklichen zu können, wird ein Satz von elementaren Funktionen
benötigt. Im folgenden werden diese Grundfunktionen vorgestellt.
16.1
79
Elektronik und Prozessmesstechnik
i11
i2
R11
---
uE 1
+
uA
Bild 1.103: Addierer
Der Negierer erzeugt ein Signal mit negativem Vorzeichen. Bei Sinussignalen spricht man
auch von gegenphasigen Signalen.
Der negative Anschluss des OPs bildet die virtuelle Masse. Folglich gilt für die
Stromsumme
(1.117)
i 11 + i 12 + i 13 + i 2 = 0 .
R1
Wenn wird die Ströme durch die Ein- und Ausgangsspannungen ersetzen, so erhalten wir
R1
uE1 u E2 u E3 u A
+
+
+
=0.
R 11 R 12 R 13 R 2
--uE
+
Auflösen nach uA liefert
uA
uA = −
Bild 1.102: Negierer
R1
u = − uE .
R1 E
(1.116)
Die Funktion hängt vom absoluten Wert der Widerstände nicht ab; beide Widerstände
müssen lediglich gleich sein. Durch ungleiche Werte entsteht ein invertierender Verstärker.
16.2


R2
R
R
u + 2u + 2u
.
R 11 E1 R 12 E2 R13 E3
(1.119)
Für den häufigen Fall, dass alle Widerstände identisch gewählt werden, erhält man
Ein- und Ausgangsspannung verwenden den negativen Eingang (zwecks Gegenkopplung).
Der Zusammenhang zwischen Ein- und Ausgang lautet
uA = −
(1.118)
Addierer
Der Addierer ist ein Element, dass Signale addiert. Gleichzeitig wird der Ausgang negiert,
was schaltungstechnisch nicht zu vermeiden ist.
u A = − u E1 + u E2 + u E3 .
16.3
(1.120)
Subtrahierer
Häufig ist es erforderlich, die Differenz zweier Signale zu bilden (z.B. bei der Bildung der
Regelabweichung in einem Regelkreis). Die Differenz kann durch Verwendung eines
Negierers und eines Addierers verwirklicht werden.
E K. Müller
Elektronik und Prozessmesstechnik
80
E K. Müller
Hochschule Bremerhaven --- IAE
R
R
R
--+
Hochschule Bremerhaven --- IAE
k 1 :=
∂u A
≠ f (u E2)
∂u E1
(1.123)
k 2 :=
∂u A
≠ f (u E1) .
∂u E2
(1.124)
sowie
ux
R
--uE 2
+
uA
Die Ausgangsgröße entsteht dann durch Überlagerung der Eingangsspannungen gebildet
werden
(1.125)
u A = k 1uE1 + k 2u E2 .
Bild 1.104: Subtrahierer
Zur Vereinfachung werden alle Widerstände gleichgesetzt. Damit ist die Verstärkung 1 für
alle Signale. Es gelten die Gleichungen für den Negierer und den Addierer
u x = − u E1 ,
81
Die Berechnung der Schaltung kann nach dem Überlagerungsprinzip erfolgen, da die
Operationsverstärker-Schaltungen linear sind. Linearität bedeutet, dass
R
uE 1
Elektronik und Prozessmesstechnik
u A = − u x + u E2 .
Wir können zur Bestimmung von k1 somit uE2 nullsetzen. Die dazu gehörende Schaltung
zeigt Bild 1.106.
R11
(1.121)
Nach Einsetzen von ux in die zweite Gleichung erhält man
uE 1
u A = − − u E1 + u E2 = u E1 − u E2 .
(1.122)
Es ist jedoch nicht ökonomisch, für diese Funktion zwei OPs zu verwenden. In der Praxis
verwendet man deshalb folgende Schaltung, die die gleiche Funktion mit nur einem
Operationsverstärker ermöglicht. Für diese Funktion gibt es auch spezielle ICs
(z.B. LF352).
R11
uE 1
R12
R21
--+
uA
Bild 1.106: Ersatz-Schaltung zur Bestimmung von k1
Die Schaltung in Bild 1.106 ist der bekannte invertierende Verstärker in Gegenkopplung
mit Beziehung
uA = −
--+
R12
uA
R22
uE 2
Bild 1.105: Subtrahierer mit einem Operationsverstärker (Instrumentationsverstärker)
R 12
u .
R 11 E1
(1.126)
E K. Müller
82
Elektronik und Prozessmesstechnik
R11
Hochschule Bremerhaven --- IAE
R12
E K. Müller
Elektronik und Prozessmesstechnik

---
R 12
R 11

R 22
u .
R 21 + R 22 E2
(1.129)
Durch Überlagerung von (1.129) und (1.126) erhält man die vollständige Beziehung
+
uA

uA = 1 +
R22
R 12
R 11

R 22
R
u − 12 u .
R 21 + R 22 E2 R 11 E1
(1.130)
Wählt man nun R12 = α R11 und R22 = α R21, so folgt
uE 2
u A = (1 + α)
α u − αu .
E1
1 + α E2
(1.131)
Das einfache Ergebnis lautet damit endgültig
Bild 1.107: Ersatz-Schaltung zur Bestimmung von k2
u A = α u E2 − α u E1 = α u E2 − u E1 .
Das Bild 1.107 zeichnet man in eine gebräuchliche Form um (Bild 1.108).
(1.132)
Sind alle Widerstände gleich, so erhält man aufgrund von α = 1
R21
ux
uE 2
Hochschule Bremerhaven --- IAE
Fasst man beide Gleichungen zusammen, so folgt
uA = 1 +
R21
83
R22
(1.133)
u A = u E2 − u E1 .
+
--R12
uA
16.4
Integrator
In Regelsystemen ist ein Integrator oft Bestandteil des Reglers. Das (negative) Integral der
Eingangsgröße liefert die Schaltung in Bild 1.109.
R11
C
i1
Bild 1.108: Ersatz-Schaltung zur Bestimmung von k2 (Umzeichnung von Bild 1.107)
R 22
u .
R 21 + R 22 E2
(1.127)


uE
+
uA
Bild 1.109: Integrator
Mit der virtuellen Masse am negativen Anschluss folgt für
Die Ausgangsspannung folgt aus ux
R
u A = 1 + 12 u x .
R 11
R
---
Diese vorstehende Schaltung lässt sich auf den bekannten nicht-invertierenden Verstärker
(Elektrometer-Verstärker) zurückführen. Die Eingangsspannung liegt jedoch nicht direkt
an dem positiven Anschluss des OPs an, sondern über den aus R21 und R22 gebildeten
(unbelasteten) Spannungsteiler
ux =
i2
(1.128)
i1 =
uE
R
und für den Strom
(1.134)
E K. Müller
84
Elektronik und Prozessmesstechnik
i2 = C
Hochschule Bremerhaven --- IAE
du A
.
dt
(1.135)
Da kein Strom in den negativen Anschluss des OP fließt (idealer OP), gilt natürlich
(1.136)
i1 + i2 = 0 ,
E K. Müller
85
Elektronik und Prozessmesstechnik
16.5
Differenzierer
Wird die Ableitung eines Signals benötigt (z.B. für einen Regler), so setzt man einen
Differenzierer ein, der aus dem “Tausch” der Impedanzen im Eingangszweig und der
Rückführung folgt.
R
oder durch die Spannungen ausgedrückt
uE
du
+C A =0.
R
dt
(1.137)
i1
--uE
(1.138)
Die Integration auf beiden Seiten ergibt die Spannung
 u (τ)dτ + u (0) .
E
A
+
uA
Bild 1.110: Differenzierer
t
uA = − 1
RC
i2
C
Auflösen nach der Ableitung des Ausgangsstroms gibt
u
du A
=− E .
RC
dt
Hochschule Bremerhaven --- IAE
(1.139)
0
Auf gleiche Weise wie im Abschnitt 16.4 folgt
i1 = C
Der Ausgang ist somit das (negative) Integral des Eingangs.
du E
dt
(1.143)
und für den Strom
Der Faktor RC wird als (Integrier-) Zeitkonstante Ti bezeichnet.
i2 =
Die Frequenzabhängigkeit des Integrators erhält man mit Hilfe der komplexen Impedanz
des Kondensators
ZC = 1 .
jωC
(1.140)
(1.144)
Da kein Strom in den negativen Anschluss des OP fließt (idealer OP), gilt wieder
(1.145)
i1 + i2 = 0 ,
oder durch die Spannungen ausgedrückt
Die komplexe Verstärkung lautet damit
Z
A=− C=− 1 .
R
jωRC
C
(1.141)
du E u A
+
=0.
R
dt
(1.146)
Die Ausgangsspannung ist demnach
Der Faktor ---1 / j = +j bedeutet eine Phasendrehung von 90˚ der Ausgangsspannung
gegenüber der Eingangsspannung (Phasenvoreilung).
Der Betrag von A ist
A = |A| =
uA
.
R
u A = − RC
du E
.
dt
(1.147)
Die komplexe Verstärkung folgt aus der Impedanz des Kondensators
1 .
ωRC
(1.142)
Die Verstärkung nimmt also mit der Frequenz stetig ab, d.h. hohe Frequenzen werden
unterdrückt.
ZC = 1 ,
jωC
(1.148)
A = − R = − jωRC .
ZC
(1.149)
E K. Müller
86
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Die Verstärkung nimmt mit zunehmender Frequenz stetig zu.
E K. Müller
87
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Die sogenannte Grenzfrequenz
ωg = 1
R 2C
Der Faktor ---j bedeutet eine Phasendrehung von 90˚ der Ausgangsspannung gegenüber
der Eingangsspannung (Phasennacheilung).
(1.154)
bzw.
16.6
Tiefpassfilter
fg =
Das folgende Bild zeigt ein aktives Tiefpassfilter 1. Ordnung.
C
ωg
= 1
2π
2πR 2C
(1.155)
ist die Frequenz, bei der der Betrag der Verstärkung von
A max =
Z2
R2
R1
(1.156)
auf
R2
R1
A max
2
--UE
+
(1.157)
abgefallen ist. Die Verstärkungsänderung um den Faktor 1∕ 2 entspricht etwa ---3dB im
logarithmischen Verhältnismaß DeziBel
UA

d = 20 ⋅ log 10 1 = − 3.0103dB ≈ − 3dB .
2
(1.158)
Bild 1.111: Tiefpassfilter
Die (komplexe) Verstärkung ist das Verhältnis der Impedanz in der Rückführung durch die
Impedanz im Eingangszweig (in diesem Fall nur R1). Man erhält
A=−
Z2
Z
=− 2 .
Z1
R1
(1.150)
16.7
Hochpassfilter
Ein sogenanntes aktives Hochpassfilter folgt aus dem Tiefpassfilter durch Austausch der
Impedanzen im Eingangszweig und in der Rückkopplung. Die Parallelschaltung von R und
C ist zusätzlich in eine Reihenschaltung zu wandeln.
Die Impedanz ist Z2 ist die Parallelschaltung aus R2 und C
Z2 =
1
R2
R2
1
=
.
1 + jωR 2C
+ jωC
(1.151)
UE
(1.152)
Für den Betrag der Verstärkung gilt
R
|A| = 2
R1
1
1 + ωR2C 2
R1
Z1
R2
---
und damit gilt
Z
R
1
A=− 2=− 2
.
R1
R 1 1 + jωR 2C
C
+
UA
Bild 1.112: Hochpassfilter
.
(1.153)
Die (komplexe) Verstärkung ist das Verhältnis der Impedanz in der Rückführung durch die
Impedanz im Eingangszweig. Man erhält
E K. Müller
88
Elektronik und Prozessmesstechnik
A=−
Hochschule Bremerhaven --- IAE
Z2
R
=− 2 .
Z1
Z1
(1.159)
Zunächst muss jedoch die Impedanz Z1 ermittelt werden
1 + jωR1C
.
Z1 = R 1 + 1 =
jωC
jωC
(1.160)
Damit folgt für die komplexe Verstärkung nach (1.159)
A=−
R2
jωR 2C
R
jωR 1C
=−
=− 2
.
Z1
R 1 1 + jωR 1C
1 + jωR 1C
E K. Müller
89
Elektronik und Prozessmesstechnik
Widerstände für Operationsverstärker-Schaltungen liegen im Bereich mehrerer kΩ . Die
Schaltung wird dann durch die Widerstände nicht belastet. Die Widerstände müssen jedoch
klein gegenüber den Eingangswiderständen des OPs gewählt werden.
Die Auswahl der Widerstände muss sich aber auch an der Verfügbarkeit orientieren, d.h.
man sollte nur Widerstände wählen, die in der E-12-Reihe enthalten sind. Dadurch können
aber Verstärkungsverhältnisse u.U. nicht exakt eingehalten werden. Müssen Werte exakt
eingehalten werden, so setzt man Potentiometer anstelle von Festwiderständen ein. Eine
andere Möglichkeit sind Parallel- oder Serienschaltungen von Widerständen.
(1.161)
Der Betrag lässt sich durch Betragsbildung von Zähler und Nenner ermitteln
A = |A| =
R2
R1
ωR 1C
1 + ωR1C 2
.
C
(1.162)
Z2
R2
R1
---
Die sogenannte Grenzfrequenz
ωg = 1
R 1C
Hochschule Bremerhaven --- IAE
(1.163)
UE
+
UA
bzw.
fg =
ωg
= 1
2π
2πR 1C
(1.164)
Die Verstärkung (Betrag) für tiefe Frequenzen ist gegeben durch
ist die Frequenz, bei der der Betrag der Verstärkung von
A max =
R2
R1
(1.165)
auf
A max
2
(1.166)
abgefallen ist. Die Grenzfrequenz nennt man auch 3dB-Frequenz.
17
Bild 1.113: Tiefpassfilter
Beispiele für aktive Filter
A max =
R2
R1
(1.167)
Ein ungefähres Verhältnis von 2 liefern die Widerstände R1 = 33kΩ und R2 = 68kΩ.
Man erhält
A max = 68kΩ = 2.061 .
33kΩ
(1.168)
Die Grenzfrequenz des Tiefpass ist gegeben durch
fg =
ωg
= 1
.
2π
2πR 2C
(1.169)
Da R2 bereits festgelegt wurde, muss nun C bestimmt werden
17.1
(1)
Tiefpassfilter: Verstärkung 2, Grenzfrequenz 40Hz
Bestimmen Sie die Widerstände und den Kondensator für ein aktives Tiefpassfilter
mit einer Verstärkung für tiefe Frequenzen (f ≪ fg ) von A = 2. Die Grenzfrequenz
soll 40Hz betragen.
C=
1 =
1
= 58.51nF .
2πR 2f g
2π68kΩ40 1s
(1.170)
Der nächste Kondensator in der E12-Reihe wäre 56nF. Mit diesem Kondensator wäre die
Grenzfrequenz
E K. Müller
90
Elektronik und Prozessmesstechnik
fg =
17.2
(1)
Hochschule Bremerhaven --- IAE
1
= 41.8Hz .
2π 68kΩ 56nF
(1.171)
E K. Müller
91
Elektronik und Prozessmesstechnik
17.3
Hochschule Bremerhaven --- IAE
Professionelles Tiefpassfilter für 1kHz
Hochpassfilter: Verstärkung 0.8, Grenzfrequenz 5Hz
Bestimmen Sie die Widerstände und den Kondensator für ein aktives
Hochpassfilter mit einer Verstärkung für tiefe Frequenzen (f ≪ fg ) von A = 0,8.
Die Grenzfrequenz soll 5Hz betragen.
Unter Verstärkung des Hochpassfilters versteht man das Verhältnis der Spannungen
zwischen Ausgang und Eingang für hohe Frequenzen, d.h. für f ≫ fg .
C
R1
Z1
R2
---
UE
+
Bild 1.115: Tiefpassfilter 4. Ordnung mit E-12-Werten (E Texas Instruments)
UA
Mit einem OP lässt sich ein Tiefpassfilter 2. Ordnung erzeugen (Mehrfach-Gegenkopplung). Für ein Filter 4. Ordnung benötigt man somit 2 OPs.
Bild 1.114: Hochpassfilter
Aus dem Betrag der Verstärkung folgt das Widerstandsverhältnis
|A| =
R2 !
= 0.8 .
R1
(1.172)
Man findet innerhalb der E-12-Reihe die Widerstände R1 = 15kΩ und R2 = 12kΩ, die
exakt das gewünschte Verhältnis ergeben.
Nun ist bereits R1 = 15kΩ festgelegt. Löst man (1.164) nach dem Kondensator auf, so
erhält man
1
1
=
= 2.122μF .
C=
2πR 1 f g
2π 15kΩ 5 1s
18
Messschaltungen
18.1
Gleichrichterschaltungen
Mit aktiven Gleichrichterschaltungen lassen sich präzise Gleichrichter verwirklichen, die
nicht durch Spannungsabfälle an Dioden verfälscht werden. Man unterscheidet zwischen
Einweg- und Zweiweggleichrichtung.
UA
UA
(1.173)
Der nächste E-12-Wert wäre 2.2μF. Die Grenzfrequenz lautet damit
fg =
1
= 4.8Hz .
2π 15kΩ 2.2μF
(1.174)
Da man die Grenzfrequenz in einem gewissem Abstand zum Nutzfrequenzbereich legt, ist
eine genaue Einhaltung der Grenzfrequenz i.a. nicht erforderlich.
Einweg-Gleichrichtung
UE
Bild 1.116: Ein- und Zweiweg-Gleichrichtung
Zweiweg-Gleichrichtung
UE
E K. Müller
92
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Bei der Einweg-Gleichrichtung wird nur die positive Spannung übertragen; bei negativer
Eingangsspannung bleibt die Ausgangsspannung null. Bei der Zweiweggleichrichtung
erzeugt die negative Eingangsspannung eine positive Ausgangsspannung gleicher
Amplitude.
18.1.1
E K. Müller
 − uE
0
u A= = 
für u E > 0
,
für u E < 0
(1.179)
i3
uE
D2
R
(1.178)
ersetzt man den Strom i2 gemäß (1.175) und (1.176), so folgt
i2
i1
Hochschule Bremerhaven --- IAE
u A= = − R 2i 2 .
Präzisions-Einweggleichrichter
R
93
Elektronik und Prozessmesstechnik
--uE
+
D1
uA=
uA=
Bild 1.117: Präzisions-Einweggleichrichter
Bild 1.118: Ein- und Ausgangsspannung der Schaltung aus Bild 1.117
In Bild 1.117 ist ein invertierender Einweg-Gleichrichter gezeichnet, d.h. die
Ausgangsspannung ist negativ. Man beachte, dass der Ausgang der Schaltung nicht der
Ausgang des OPs ist, damit die Spannung an der Diode die Gleichrichtung nicht verfälscht.
Der OP erzeugt wieder einer virtuelle Masse an seinem negativen Anschluss. Für den
Strom i1 gilt folglich
i1 =
uE
.
R
(1.175)
Aufgrund der Dioden sind i2 und i3 von der Stromrichtung von i1 bzw. von dem
Vorzeichen von uE abhängig
 i1
0
i2 = 
für i1 > 0
,
für i 1 < 0
0
 − i1
i3 = 
für i 1 > 0
.
für i 1 < 0
Die Ausgangsspannung ist (aufgrund der Wirkung der virtuellen Masse)
18.1.2
Präzisions-Zweiweggleichrichter
Eine Zweiweggleichrichter erhält man, indem man die Signale in Bild 1.118 geeignet
subtrahiert
(1.180)
u A = − u E + 2u A= .
-uE
2uA=
(1.176)
(1.177)
Bild 1.119: Signale der Gleichung (1.180)
Das Ergebnis der Addition ist im folgenden Diagramm dargestellt
E K. Müller
94
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
E K. Müller
95
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Der Effektivwert bezieht sich immer auf den Mittelwert der Leistung, d.h. man teil die
Energie durch ein Zeitinterval
uA2
T
P=W=
T
 p(τ)dτ
0
(1.182)
.
∆t
Es muss also die Leistung integriert werden (Energie) und durch das Zeitinterval geteilt
werden, über das integriert wurde. Zweckmäßigerweise beschränkt man das Zeitinterval
auf die Periodendauer zu zu untersuchenden Signals.
Bild 1.120: Ergebnis der Addition in Bild 1.119
Die Subtraktion erfolgt unter Verwendung des invertierenden Einweggleichrichters mit
einem Addierer.
2R
Damit muss
T
U 2eff
=1
R
T
2R
 u R(τ) dτ
2
(1.183)
0
gelten. Da das Ergebnis hängt von R nicht ab; wenn beide Seiten mit R multipliziert
werden, erhält man die Definitionsgleichung für Ueff .
R
T
U 2eff
D2
R
bzw.
---
+
D1
Einweg-Gleichrichter
 u (τ)dτ .
(1.184)
2
0
R
--uE
=1
T
+

T
uA
U eff =
1
T
(1.185)
u 2(τ)dτ .
0
Addierer
Bei Sinusgrößen
Bild 1.121: Präzisions-Zweiweggleichrichter
Die Ausgangsspannung ist allerdings im Gegensatz zu Bild 1.120 negativ, da der Addierer
invertierend ist.
^
sin(ωt) ,
u(t) = u
^
u
= Scheitelwert
(1.186)
ist es einfacher, über den Winkel τ = ωt zu integrieren, d.h. man erhält

2π
19
U eff =
Effektivwertmessung
.
p(t) = u(t)i(t) = u u =
R
R
 u^ sin(τ) 
2
dτ .
(1.187)
0
Der Effektivwert (RMS = root mean square) ist der äquivalente Gleichstrom, der die
gleiche Leistung an einem ohmschen Verbraucher abgibt, wie das zu untersuchende Signal.
Der Augenblickswert der Leistung an einem Widerstand ist
u2
1
2π
(1.181)
Der Scheitelwert kann auch vor die Wurzel gezogen werden

2π
^
U eff = u
1
2π
0
sin 2(τ)dτ .
(1.188)
E K. Müller
96
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
E K. Müller
Da über das Quadrat des Sinus integriert wird, genügt auch die Mittelwertbildung über die
halbe Periodendauer
^
U eff = u

U eff =
π
1
π
 sin (τ)dτ .
(1.189)
2
0
Ersetzt man
(1.190)
so folgt

1
2π
1 − cos(2τ)dτ .


1 τ − 1 sin(2τ)
2
2π

π
0
^
=u
12 .
(1.191)
U eff = u
2
−T∕4

T∕4
^
1 1 t3
= u .
3
T∕2 3 −T∕4
(1.194)
Näherungsweise Effektivwertmessung über den
Betragsmittelwert
T∕2
 u(t)dt .
U := 1
T
(1.192)
Das Suffix “eff” kann auch entfallen. Das Verhältnis zwischen Scheitelwert und
Effektivwert nenn man Crest-Faktor
^
Crest−Faktor = u = 2
U eff
^
Der Betragsmittelwert bei einem periodischen Signal ist
Der Effektivwert ist somit um den Faktor 2 kleiner als der Scheitelwert
^
2
 T∕4u t  dt
Der Effektivwert wird häufig über den Betragsmittelwert bestimmt, da der Unterschied
zwischen Betragsmittelwert und Effektivwert nicht so stark von der Kurvenform abhängt
wie bei Scheitelwert und Effektivwert (Crest-Faktor).
0
^
=u
Hochschule Bremerhaven --- IAE
Der Crest-Faktor für Dreieckspannungen ist somit 3 . Aus einer Messung des
Scheitelwertes kann also kaum auf den Effektivwert geschlossen werden.
19.1
π
^
U eff = u

T∕4
1
T∕2
^
= u
T∕4
sin 2 x = 1 1 − cos(2x) ,
2
97
Elektronik und Prozessmesstechnik
(1.195)
−T∕2
Dabei ist T die Periodendauer. Für Sinusgrößen genügt es, das Intervall auf die halbe
Periodendauer zu erstrecken, da die zweite Hälfte den gleichen Verlauf wie die Erste
aufweist. Weiterhin bietet sich wieder an, die Integration über den Winkel τ durchzuführen
π
(für Sinusgrößen) .
(1.193)
1
U=π
 u sin(τ)dτ = πu − cos(τ)
^
^
π
0
2u
^
=π
.
(1.196)
0
^
u
−T
4
uD
T
4
^
^
U eff = u = 0.7071u
2
^
u
^
^
2u
U=π
= 0.6366u
T
T
Bild 1.122: Dreiecksignal
Für Dreiecksignale gilt beispielsweise ein anderer Crest-Faktor. Hier gilt
Bild 1.123: Scheitelwert, Effektivwert und Betragsmittelwert bei Sinusgrößen
E K. Müller
98
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
^ 
Bei einer Dreieckspannung war der Effektivwert (1.194) U eff = u
∕ 3 .
Der
Betragsmittelwert folgt ohne Berechnung zu
^
U=u ,
2
(1.197)
da ja die Flächen ober und unterhalt des halben Scheitelwerts gleich sind.
^
u
|uD |
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
verwenden.
Viele Messgeräte messen Effektivwerte über den Betragsmittelwert und korrigieren
dies mit dem Faktor 1,111 (z.B. in der Skala zur Anzeige). Bei Kurvenformen, die von
der Sinusform abweichen, tritt ein systematischer Messfehler auf (Ausnahme:
Messgeräte mit der Angabe “True RMS”).
Beispiele:
Eine Messeinrichtung für sinusförmige Spannungen misst einen Effektivwert für
Dreiecksignale, der um den Faktor
^
U=u
2
(U eff∕U) Sinus
T
(U eff∕U) Dreieck
Bild 1.124: Betragsmittelwert des Dreiecksignals
Damit gelten für die Dreieckfunktion die Zusammenhänge in Bild 1.125.
^
^
U eff = u = 0.5774u
3
^
u
99
= 1.111 = 0.9619
1.155
zu klein ist. Der Messfehler beträgt damit etwas 4%. Bei anderen Kurvenformen kann der
Fehler stark anwachsen. Misst man z.B. den Effektivwert von Gleichstrom oder
Rechtecksignalen mit einer Messschaltung für Sinusspannungen, so ist die Messung um den
Faktor
(U eff∕U) Sinus
^
^
U = 1u
= 0.5u
2
(U eff∕U) Rechteck
T
(1.200)
= 1.111 = 1.111
1
(1.201)
zu groß. Der Messfehler beträgt damit mehr als 11%.
Eine echte Effektivwertmessung muss die Mittelwertbildung über das Quadrat der
Spannung beinhalten.
Bild 1.125: Scheitelwert, Effektivwert und Betragsmittelwert bei der Dreieckfunktion
Man erkennt, dass auch für Kurvenformen, die etwas von der Sinusform abweichen,
Effektivwert und Betragsmittelwert sich nicht wesentlich unterscheiden. Eine praktikable
Effektivwertmessung erhält man also, wenn man den Betragsmittelwert misst (einfach) und
ihn mit dem Faktor
U eff
U
^
=
u
2
=
2^
πu
π = π = 1.111 ,
8
2 2
(Sinusgrößen)
(1.198)
multipliziert.
Die Korrektur mit dem Faktor 1,111 gilt nur für Sinusgrößen!
Bei der Dreieckfunktion müsste man den Faktor
U eff
U
=
^
u
3
=
1^
u
2
2 = 1.155 ,
3
(Dreieckfunktion)
(1.199)
20
Scheitelwertmessung
Ein häufige Messaufgabe ist Bestimmung eines Maximalwertes eines ansonsten beliebigen
Verlaufs der Spannung oder des Stroms. Man bezeichnet diesen Vorgang als
Scheitelwertmessung. Eine mögliche Schaltung zeigt Bild 1.126.
E K. Müller
E K. Müller
100
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
21
R1
+
Analoge und digitale Systeme
R2
--uE
101
Hochschule Bremerhaven --- IAE
Unter System verstehen wir Einrichtung oder Anlage, die aufgrund einer Einwirkung
(Eingangssignal) eine Wirkung an seinem Ausgang als Folge des Eingangssignals erzeugt.
D2
R1
Elektronik und Prozessmesstechnik
Eingang
+
D1
OP1
uX
---
RC
T
C
OP2
uA
Bild 2.1:
System
Ausgang
System
Unter einem analogen System verstehen wir ein System, bei dem die Signale jeden
beliebigen Wert innerhalb eines kontinuierlichen Wertebereichs annehmen können und
diese Werte auch von technischer Bedeutung sind (Beispiel: Temperatur eines Backofens).
uC
Bei Digitale Systemen nehmen die Signale auch kontinuierliche Werte an. Jedoch
interessieren hier nur zwei Werte:
Bild 1.126: Präzisions-Scheitelwertmessung
Das Prinzip der Schaltung beruht auf der Speicherung der maximalen Amplitude auf dem
Kondensator C. Der Taster T dient nur zum Entladen des Kondensators über den
Widerstand RC , um eine neue Messung durchführen zu können. Der Kondensator würde
sonst den Scheitelwert (negativ!) theoretisch beliebig lange speichern, da er weder über den
OP2 noch über die Diode D1 in Sperrrichtung entladen werden könnte.
Für positive Eingangsspannungen uE leitet die Diode D1 (Ausgangsspannung von OP1
ist negativ). Damit wird der Kondensator auf die negative Spannung
uC = uA = − uE
(1.202)
aufgeladen. OP2 ist ein Verstärker mit A = 1, so dass uC = uA eingehalten wird. Die
Bedingung uA = ---uE folgt aus der Rückkopplung des invertierend geschalteten OP1
über R1.
Nimmt die Spannung uE wieder ab, so wird uX größer. Dadurch sperrt D1 und die
Rückkopplung über OP2 und R1 wird aufgehoben. Der Operationsverstärker OP1 würde
ohne die Diode D2 aufgrund seiner unendlichen Verstärkung seine positive
Maximalspannung ausgeben. Die Diode D2 verhindert diesen Zustand und begrenzt die
Ausgangsspannung uX auf kleine Spannungen (ca. 0,6---0,7V).
Bei einem digitalen System interessieren nur zwei Werte oder Zustände der Ein- und
Ausgangssignale: 0 oder 1, bzw. TRUE oder FALSE, ON oder OFF bzw. LOW oder
HIGH.
Häufig werden bei digitalen Systemen wieder kontinuierliche Signale benötigt (z.B.
CD-Player). Diese Aufgabe übernehmen Digital-Analog-Umsetzer (DAC) bzw.
Analog-Digital-Umsetzer (ADC).
Man bezeichnet die analoge Ein-/Ausgangssignale auch als koniuierliche Signale.
Bei einem digitalen System spricht man auch von diskreten Signale, die nur die
diskreten Werte 0 bzw. 1 annehmen.
Mit anderen Worten: Wir tun so, als wenn bei einem digitalen System nur zwei verschiedene
Werte auftreten.
Die Vorteile der Digitaltechnik gegenüber einer Verwirklichung mit analogen Schaltungen
sind jedoch so immens, dass immer mehr analoge Funktionen durch digitale Systeme
ersetzt werden. Beispiele:
Langspielplatte → CD-Player
Kamera mit Film → Digitalkamera
Darüber hinaus können mit digitalen Systemen neue Funktionen verwirklicht werden
(Computer, ABS / ESP sowie digitale Motorsteuerung bei Kraftfahrzeugen, digitale
Nachrichtenübermittlung bei Mobiltelefonen oder im Fernseh- und Rundfunkbereich).
Wichtige Vorteile der Digitaltechnik gegenüber analogen Ausführungen:
E K. Müller
102
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
22.2
S
Hohe Flexibilität durch Programmierbarkeit
S
Möglichkeit, beliebig komplexe Funktionen zu realisieren
S
Störungsfreie Übertragung und Signalverarbeitung (DAB bzw. DVB Rundfunk)
22
E K. Müller
Digitalschaltungen
Elektronische Digitalschaltungen bestehen überwiegend aus TTL- (Transistor-Transistor
Logic) oder CMOS- (Complementary Metal-Oxyde Semiconductor) Bauelementen. Die
logischen Zustände “0” und “1” werden durch kleine bzw. große Spannungen (relativ zur
Betriebsspannung von ca. 5 V) abgebildet. Man spricht in diesem Zusammenhang auch von
HIGH und LOW. Man drückt dadurch aus, dass die logischen Zustände durch physikalische
Spannungen repräsentiert werden.
Zuordnung von “0” zu “LOW” und “1” zu “HIGH” = positive Logik
Zuordnung von “0” zu “HIGH” und “1” zu “LOW” = negative Logik
103
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Logische Signale und Funktionen (Gatter)
Unabhängig von der physikalischen Verwirklichung entwirft man oft ein digitales System
als logisches System mit logischen Signalen, d.h. “0”-“1”-Signalen. Wir ignorieren also das
elektrische Verhalten (bei CMOS- oder TTL-Schaltungen) und beschränken uns auf die
diskreten Signale 0 und 1. Bevor man also eine Schaltung aufbaut, wird zunächst das logische
Verhalten entworfen.
x
f
y
logische
Schaltung
z
Bild 2.2:
g
Logische Schaltung mit drei Eingängen und zwei Ausgängen
Die Funktion der Schaltung wird durch die sogenannte Wahrheitstabelle vollständig
beschrieben.
Die Wahrheitstabelle beschreibt vollständig eine kombinatorische logische Schaltung.
22.1
Verwirklichung digitaler Funktionen
Eine logische Funktion kann nicht nur elektronisch realisiert werden. In der folgenden
Tabelle sind gebräuchliche Technologien zusammengestellt.
Unter
kombinatorischer
Schaltung versteht man eine Schaltung, bei der die
Ausgangsgrößen ausschließlich von den Eingangsgrößen abhängen.
Schaltungen mit internen Speicherelementen heißen sequentielle Schaltungen.
Technologie
Bit = 0
Bit = 1
Pneumatik
niedriger Druck
hoher Druck
Relais
Anker abgefallen
Anker angezogen
CMOS
0---1,5V
3,5---5,0V
Die Schaltung in Bild 2.2 könnte z.B. eine einstellige Addition sein.
TTL
0---0,8V
2,0---5,0V
Wahrheitstabelle für eine einstellige duale Addition
Lichtleiter
kein Licht
Licht an
Dynamischer
Speicher
Kondensator entladen
Kondensator geladen
Biploar ROM
Sicherung zerstört
Sicherung intakt
Festplatte/
Magnetband
Flussrichtung Nord
Flussrichtung Süd
CDROM
(Read Only)
keine Vertiefung (no Pit)
Vertiefung (Pit)
CD/RW
(rewritable)
polykristalline Struktur
monokristalline Struktur
Die sequentiellen Schaltungen sind wesentlich leistungsfähiger. Jeder Computer ist eine
sequentielle Schaltung. Eine sequentielle Schaltung enthält aber immer kombinatorische
Logik. Es ist deshalb sinnvoll, sich zunächst mit kombinatorischer Logik zu befassen.
Eingänge
Ausgänge
x = carryin
y = xk
z = yk
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
f = xk +yk
0
1
1
0
1
0
0
1
g = carryout
0
0
0
1
0
1
1
1
E K. Müller
104
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
Beliebig komplexe Schaltungen lassen sich aus wenigen elementaren Logikfunktionen
(=Gatter) aufbauen.
22.3
E K. Müller
22.3.3
Es werden jeweils die gültigen IEC-Symbole aufgelistet als auch die veralteten
amerikanischen Schaltzeichen. Alte deutsche Symbole werden weggelassen. Die alten
amerikanischen Symbole sind auch heute weit verbreitet, insbesondere bei ECAD-Software (Electronic Computer Aided Design).
a
b
≥1
Die folgenden Gatter werden nur mit der minimalen Anzahl von Eingangsgrößen
gezeichnet. Der Erweiterung auf mehrere Eingangsgrößen ist jedoch einfach.
Übung: Zeichnen Sie Gatter mit jeweils drei Eingangsgrößen und geben Sie die
entsprechende Wahrheitstabelle an.
22.3.1
22.3.4
a
x
a
b
x
a
Wahrheitstabelle
a
x
0
1
1
0
x
Wahrheitstabelle
a
x
b
0
0
0
0
1
1
1
0
1
1
1
1
DIN-Schreibweise:
x = a∨b
(x = a oder b)
amerik. Schreibweise:
x = a+b
(x = a or b)
NAND
&
a
b
amerik. Symbol
x
a
b
x
Boolsche Funktion
amerik. Symbol
1
x
Symbol
Inverter (Negation)
Symbol
amerik. Symbol
Boolsche Funktion
Variablen mit den Zuständen 0 und 1 bezeichnet man als boolsche Variablen.
Die Rechenreglen mit boolschen Variablen heißen boolsche Algebra.
Hochschule Bremerhaven --- IAE
Disjunktion (OR)
Symbol
Elementare Gatter
105
Elektronik und Prozessmesstechnik
Wahrheitstabelle
a
x
b
0
0
1
0
1
1
1
0
1
1
1
0
DIN-Schreibweise:
x = a∧b
amerik. Schreibweise:
x = (a ⋅ b )′ (x = a nand b)
Mit NAND-Gattern lassen sich beliebige logische Funktionen realisieren.
Boolsche Funktion
22.3.2
DIN-Schreibweise:
x=y
(x = nicht a)
amerik. Schreibweise:
x = a′
(x = not a)
&
amerik. Symbol
x
NOR
Symbol
Konjunktion (AND)
Symbol
a
b
22.3.5
a
b
x
Boolsche Funktion
Wahrheitstabelle
a
x
b
0
0
0
0
1
0
1
0
0
1
1
1
DIN-Schreibweise:
x = a∧b
(x = a und b)
amerik. Schreibweise:
x = a⋅b
(x = a and b)
a
b
≥1
amerik. Symbol
x
a
b
x
Boolsche Funktion
Wahrheitstabelle
a
x
b
0
0
1
0
1
0
1
0
0
1
1
0
DIN-Schreibweise:
x = a∨b
amerik. Schreibweise:
x = (a + b )′ (x = a nor b)
Mit NOR-Gattern lassen sich beliebige logische Funktionen realisieren.
E K. Müller
106
Elektronik und Prozessmesstechnik
22.3.6
Hochschule Bremerhaven --- IAE
Antivalenz (exklusiv ODER, XOR)
Symbol
=1
a
b
amerik. Symbol
x
a
b
x
Boolsche Funktion
22.3.7
Wahrheitstabelle
a
x
b
0
0
0
0
1
1
1
0
1
1
1
0
DIN-Schreibweise:
x = a  b = ( a ∧ b ) ∨ a ∧ b
amerk. Schreibweise:
x = ( a  b ) (x = a xor b)
Equivalenz (XNOR)
Symbol
=1
a
b
amerik. Symbol
x
a
b
x
Boolsche Funktion
22.4
E K. Müller
Elektronik und Prozessmesstechnik
Wahrheitstabelle
a
x
b
0
0
1
0
1
0
1
0
0
1
1
1
DIN-Schreibweise:
x = a  b = a ∧ b ∨ ( a ∧ b )
amerik. Schreibweise:
x = ( a  b )′ (x = a xnor b)
Vorrangregeln für boolsche Algebra
Leider sind die Vorrangregeln für Operationen international nicht einheitlich (die
amerikanischen Regeln unterscheidet sich von von DIN 66000). Dies folgt aus der
amerikanischen Schreibweise für UND (S) und ODER (+), die der UND-Verknüpfung
eine höhere Priorität (Multiplikationszeichen) als der ODER-Verknüpfung (Summenzeichen) einräumt. Die deutsche DIN 66000 sieht UND und ODER als gleichwertig an. In der
DIN 660000 müssen also Klammern gesetzt werden, die im Amerikanischen entfallen
können.
Wir wollen uns in diesem Skript der amerikanischen Schreibweise anschließen, um bei den
späteren Software-Übungen nicht umlernen zu müssen.
Prioritätsregeln
1.
2.
3.
Negation
Konjunktion (UND)
Adjunktion (ODER)
a
a∧b
a∨b
107
Hochschule Bremerhaven --- IAE
4.
NAND
a∧b
5.
6.
7.
NOR
Äquivalenz
Antivalenz (XOR)
a∨b
a≡b
ab
Im Zweifel kann durch Klammernsetzung immer eine eindeutige Funktion angegeben
werden.
22.5
Funktionen für eine Variable (UNARY OPERATORS)
Eingang
a=1 0
Ausgang x
Symbol
Bezeichnung
0
1
0
1
x=0
x=a
x=a
x=1
Konstante 0
Identität
Negation
Konstante 1
Bild 2.3:
0
0
1
1
Unary Operators
E K. Müller
108
Elektronik und Prozessmesstechnik
22.6
Hochschule Bremerhaven --- IAE
E K. Müller
Elektronik und Prozessmesstechnik
Funktionen für zwei Variablen (BINARY
OPERATORS)
Eingänge
a= 1010
b= 1100
Ausgang x
Symbol
Bezeichnung
0000
0001
0010
0011
0100
0101
0110
0111
1000
1001
1010
1011
1100
1101
1110
1111
x=0
x = a∨b
x = a∧b
x=b
x = a∧b
x=a
x = ab
x = a∧b
x = a∧b
x=a≡b
x=a
x = a∨b
x=b
x = a∨b
x = a∨b
x=1
Konstante 0
NOR
Inhibition
Negation (b)
Inhibition
Negation (a)
XOR (Antivalenz)
NAND
UND (Konjunktion
Äquivalenz
Identität (a)
Implikation
Identität (b)
Implikation
ODER (Disjunktion)
Konstante 1
Bild 2.4:
22.7
Grundverknüpfung
S
S
S
S
S
S
S
Binary Operators
Übung: Aufstellen einer Wahrheitstabelle
Geben Sie für folgende Schaltung die Wahrheitstabelle an.
a
&
b
c
d
a∧b
≥1
1
1
c
d
&
c∧d∧e
e
Bild 2.5:
22.8
Schaltung aus einzelnen Gattern
a∧b ∨ c∧d∧e
a
b
c
d
e
a∧b
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
109
Hochschule Bremerhaven --- IAE
c∧d∧e
a∧b ∨ c∧d∧e
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Rechenregeln für eine Variable und eine Konstante
Die folgenden Rechenregeln ermöglichen oft eine erhebliche Vereinfachung von logischen
Schaltungen.
x∨0=x
(2.7)
x∨1=1
(2.8)
x∧0=0
(2.9)
x∧1=x
(2.10)
x∨x=1
(2.11)
x∧x=x
(2.12)
E K. Müller
110
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
x∨x=x
(2.13)
x∧x=x
(2.14)
x=x
(2.15)
Verwirklichung einfacher Gatterfunktionen durch
mechanische Schalter
Bild 2.9:
Zum Verständnis von Logikschaltungen ist es hilfreich, sich eine mechanische Realisierung
vorzustellen. In vielen Industrieanwendungen werden auch einfache logische Funktionen
durch Schalter (Öffner und Schließer) verwirklicht.
b
Bild 2.6:
Glühlampe
x
NAND-Gatter
a
Batterie
Bild 2.10:
Schließer
Hochschule Bremerhaven --- IAE
a
Batterie
22.9
111
Elektronik und Prozessmesstechnik
b
Glühlampe
x
NOR-Gatter
Öffner
a
Öffner und Schließer
b
Durch Drücken des Tasters wird der Schließer geschlossen (Kontakt hergestellt); durch
Drücken des Tasters auf dem Öffner wird der Kontakt geöffnet.
Eingänge:
Taster nicht gedrückt = 0
Taster gedrückt = 1
Batterie
Ausgänge: Lampe aus = 0
Lampe leuchtet = 1
Bild 2.11:
Glühlampe
x
XOR-Gatter
Übungen: Verwirklichen andere Gatterfunktionen mit mechanischen Schaltern
a
b
Batterie
Bild 2.7:
Glühlampe
x
UND-Gatter
Rechenregeln für mehrere Variablen (wichtig!)
Die Rechenregeln werden benötigt, um digitale Schaltungen zu vereinfachen, d.h. mit
minimalen Anzahl von Gatterfunktionen verwirklichen zu können.
a
Batterie
23
23.1
b
Glühlampe
x
Kommutativgesetz (Vertauschen von Operanden)
Konjunktion
x1 ∧ x2 = x2 ∧ x1
Bild 2.8:
ODER-Gatter
Disjunktion
(3.1)
E K. Müller
Elektronik und Prozessmesstechnik
112
x1 ∨ x2 = x2 ∨ x1
23.2
E K. Müller
Hochschule Bremerhaven --- IAE
Elektronik und Prozessmesstechnik
(3.2)
Assoziativgesetz (Zusammenfassen von Operanden)
Konjunktion
x 1 ∧ x 2 ∧ x 3 = x 1 ∧  x 2 ∧ x 3)
(3.3)
Disjunktion
x 1 ∨ x 2 ∨ x 3 = x 1 ∨ x 2 ∨ x 3
23.3
(3.4)
x 1 ∧ x 1 ∨ x 2 = x 1
(3.10)
x 1 ∨ x 1 ∧ x 2 = x 1 ∨ x 2
(3.11)
x 1 ∧ x 1 ∨ x 2 = x 1 ∧ x 2
(3.12)
x 1 ∧ x 2 ∨ x 1 ∧ x 2 = x 1
(3.13)
x 1 ∨ x 2 ∧ x 1 ∨ x 2 = x 1
(3.14)
Übung:
Begründen sie Kürzungsregeln mit Hilfe der vorstehenden Regeln oder der
Wahrheitstabelle.
Distributivgesetz (Verteilen von Operanden)
Konjunktion
x 1 ∧ x 2 ∨ x 3) = x 1 ∧ x 2 ∨ x 1 ∧ x 3
24
(3.5)
Disjunktion
x 1 ∨ x 2 ∧ x 3) = x 1 ∨ x 2 ∧ x 1 ∨ x 3
23.4
113
Hochschule Bremerhaven --- IAE
Mehrstufige Logik
Komplexe Logikschaltungen werden durch Hintereinanderschaltung vieler Gatter
verwirklicht. Die maximale Anzahlen von Gattern die ein Signal durchlaufen muss,
bestimmt die “Stufigkeit” n (n-stufige Logik).
(3.6)
≥1
DeMorgansche Gesetze (Negationsregeln)
=1
&
1. DeMorgansches Gesetz
x1 ∧ x2 ∧ x3 = x1 ∨ x2 ∨ x3
(3.7)
2. DeMorgansches Gesetz
x1 ∨ x2 ∨ x3 = x1 ∧ x2 ∧ x3
(3.8)
Bei DeMorgansche Gesetze fasst man zum DeMorganschen Theorem zusammen:
Die DeMorganschen Gesetze lassen sich leicht merken:
Inversion des Ausgangs ≡ Inversion aller Eingänge und Vertauschen von UND und
ODER.
23.5
Kürzungsregeln
x 1 ∨ x 1 ∧ x 2 = x 1
(3.9)
Bild 3.1:
3-stufige Logik
Es addieren sich die Durchlaufzeiten (=Propagation Delays) aller Gatter, d.h. es muss die
Summe aller Gatterlaufzeiten abgewartet werden, bis der Ausgang gültig ist. Bei modernen
Schaltkreistechnologien liegt die Gatterlaufzeit im Bereich von einigen Nanosekunden
(milliardstel Sekunden). Je schneller eine Schaltung sein muss, desto weniger Stufen darf
eine Schaltung enthalten.
25
Universelle Schaltungen mit NAND- oder
NOR-Gattern
Diese Gattertypen finden sich sehr häufig, da mit NAND- oder NOR-Gattern beliebige
kombinatorische Schaltungen aufbauen lassen. Diese Universalität folgt aus dem
DeMorganschen Theorem.
E K. Müller
114
Elektronik und Prozessmesstechnik
25.1
E K. Müller
Hochschule Bremerhaven --- IAE
Ungenutzte Eingänge
25.3
Abhängig von der Schaltkreistechnologie müssen ungenutzte Eingänge beschaltet werden,
da anderenfalls Fehlfunktionen auftreten können. Als Grundregel sollte man
berücksichtigen:
Ungenutzte Eingänge sollten nicht “offen” belassen werden.
115
Elektronik und Prozessmesstechnik
Verwirklichung von OR-Gattern mit NAND
Hier wird das DeMorgansche Theorem benötigt:
x1 ∧ x2 = x1 ∨ x2 .
(3.19)
Es müssen also die Eingänge x1 und x2 invertiert werden und in ein NAND-Gatter gegeben
werden.
x1
&
x1
Beispiel: Inverter mit NAND- oder NOR-Gatter
&
Da mit NAND und NOR beliebige Funktionen verwirklicht werden können, sind
natürlich auch Inverter möglich. Hierbei werden ein oder mehrere Eingänge der
Gatter nicht benötigt, die aber in geeigneter Weise eindeutig beschaltet werden
sollten.
Vcc ≙ 1
a
&
a
a
≥1
a
Hochschule Bremerhaven --- IAE
a
a
x2
Bild 3.3:
&
y
x2
Verwirklichung der OR-Funktion mit NAND-Gattern
Beweis:
&
a
≥1
a
y = x1 ∧ x1 ∧ x2 ∧ x2 = x1 ∧ x2 = x1 ∨ x2 .
25.4
(3.20)
Verwirklichung von AND-Gattern mit NOR
Hier wird ebenfalls das DeMorgansche Theorem angewandt:
x1 ∨ x2 = x1 ∧ x2 .
Gnd
Bild 3.2:
(3.21)
Es müssen also die Eingänge x1 und x2 invertiert werden und in ein NOR-Gatter gegeben
werden.
≙0
Inverter aus NAND- oder NOR-Gatter
x1
Der Nachweis lässt sich aus den Rechenregeln 22.8 erbringen.
a∧a= a
(3.15)
a∨a= a
(3.16)
1∧a=a
(3.17)
a∨0 = a
(3.18)
x2
Bild 3.4:
Beweis:
25.2
26
Die Verwirklichung von AND- und OR-Funktionen mit NAND und NOR ist einfach, da
lediglich ein Inverter benötigt wird, der sich auch NAND und NOR bilden lässt (s. 25.1).
x1
≥1
Auf diese Weise lassen sich Gatterschaltkreise, die oft mehrere unabhängige Gatter
enthalten, besser ausnutzen.
AND- und OR-Funktion mit NAND und NOR
≥1
≥1
y
x2
Verwirklichung der AND-Funktion mit NOR-Gattern
y = x1 ∨ x1 ∨ x2 ∨ x2 = x1 ∨ x2 = x1 ∧ x2 .
(3.22)
Normalformen
Die Normalformen sind der Schlüssel zur Verwirklichung komplexer Schaltungen mit einer
minimalen Anzahl von Gattern. Viele programmierbare Logikbausteine basieren auf einer
E K. Müller
116
Elektronik und Prozessmesstechnik
E K. Müller
Hochschule Bremerhaven --- IAE
Darstellung von Logikfunktionen in Normalform. Die Normalformen --- auch kanonische
Normalformen genannt --- lassen sich relativ leicht mit Computerprogrammen automatisch
minimieren (=optimieren im Sinne einer minimalen Anzahl von Gattern).
Elektronik und Prozessmesstechnik
117
Hochschule Bremerhaven --- IAE
y = x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x2 ∨ x 1
(3.24)
∧ x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x 2 ∨ x 1 .
Invertiert man (3.24) zweimal, so gilt die Gleichung natürlich weiterhin
Minterm: konjunktive Verknüpfung von Variablen (UND)
y = x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x2 ∨ x 1
Maxterm: disjunktive Verknüpfung von Variablen (ODER)
(3.25)
∧ x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x 2 ∨ x 1 .
Wendet man nun das DeMorgansche Theorem an
Man unterscheidet zwei (völlig gleichwertige) Normalformen
y = x 3 ∧ x 2 ∧ x 1 ∨ x 3 ∧ x 2 ∧ x 1 ∧ x 3 ∧ x2 ∧ x 1
Disjunktive Normalform (DNF): disjunktive Verknüpfung von Mintermen
(3.26)
∨ x3 ∧ x2 ∧ x1 ∨ x3 ∧ x2 ∧ x1 ,
Konjunktive Normalform (KNF): konjunktive Verknüpfung von Maxtermen
so erkennt man, das man dies auch als DNF für y auffassen kann (s. Bild 3.5)
Aus unerklärlichen Gründen findet man die DNF häufiger. Wir werden deshalb ebenfalls
die DNF-Darstellung bevorzugen. Beide Normalformen können jedoch über das
DeMorgansche Theorem leicht ineinander überführt werden. Es gibt jedoch auch Gründe
die eine oder andere Form zu wählen (Anzahl der Nullen oder Einsen in der
Wahrheitstabelle).
Bild 3.5:
x3
x2
x1
y
y
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
0
0
1
0
0
1
0
1
1
1
(3.27)
KNF = DNF für y
DNF und KNF beschreiben das Verhalten vollständig und richtig. In diesem Beispiel ist die
DNF günstiger, da weniger Terme auftreten.
Wenig Einsen → DNF, wenig Nullen → KNF
Die obige Grundregel gilt für die Verwirklichung von y. Man kann jedoch y realisieren
(mit anschließender Inversion), so dass man im Prinzip mit einer Normalform auskommt.
Bei der Verwirklichung von y finden sich weniger Nullen als Einsen, was nun eine
Darstellung in KNF nahelegt
Wahrheitstabelle für eine logische Funktion
y = x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x 2 ∨ x 1 ∧ x 3 ∨ x2 ∨ x 1 .
Für wollen die DNF und KNF für die Wahrheitstabelle 3.5 aufstellen.
(3.28)
Man benötigt lediglich einen Inverter am Ausgang, um wieder y erzeugen zu können. Die
zugehörige Schaltung zeigt Bild 3.6.
Die DNF berücksichtigt nur die Ausgänge mit “1”
Die disjunktive Zusammenfassung der “1”-Minterme liefert die DNF
y = x 3 ∧ x 2 ∧ x 1 ∨ x 3 ∧ x 2 ∧ x 1 ∨ x 3 ∧ x2 ∧ x 1 .
y = x 3 ∧ x 2 ∧ x 1 ∨ x 3 ∧ x 2 ∧ x 1 ∧ x 3 ∧ x2 ∧ x 1 .
∨ x3 ∧ x2 ∧ x1 ∨ x3 ∧ x2 ∧ x1 .
(3.23)
Die KNF berücksichtigt nur die Ausgänge mit “0”
Die konjunktive Zusammenfassung der “0”-Maxterme (Eingangsvariablen invertieren!)
liefert die KNF
E K. Müller
Elektronik und Prozessmesstechnik
118
x3
≥1
x3 ∨ x2 ∨ x1
&
≥1
y
1
x1
1
Bild 3.6:
27
x3 ∨ x2 ∨ x1
x2
x1
y
0
0
1
1
0
1
0
1
0
1
0
1
x1 0
1
0
1
1
1
Wahrheitstabelle und zugehöriges Karnaugh-Diagramm für 2 Variablen x1
und x2
x2
Minimieren (Optimieren) von
Digitalschaltungen
Bild 3.8:
Umfangreiche Digitalschaltung lassen sich algorithmisch am Rechner minimieren. Alle
modernen Programme zur Synthese digitaler Schaltungen verfügen über leistungsfähige
Algorithmen zur Minimierung des Schaltungsaufwandes (z.B. der Quine-McCluskey-Algorithmus). Kleinere Schaltungen können mit einem grafischen Verfahren, dem
Karnaugh-Veitch-Diagramm (Karnaugh-Map) minimiert werden.
Karnaugh-Diagramm: grafische Minimierung von Digitalschaltungen mit bis zu vier
Variablen
Im KV-Diagramm lässt sich das Distributivgesetz 23.3 grafisch zur Vereinfachung
auswerten. Die Gleichung
(3.29)
kann durch “Ausklammern” auf die Form
y = x1 ∧ x2 ∨ x2 = x1 ∧ 1 = x1
x2
Im KV-Diagramm werden an den entsprechenden Stellen nur Einsen (für die DNF) bzw.
nur Nullen (für die KNF) eingetragen. Die zusammenhängenden Gebiete werden
markiert.
Logikschaltung zur Wahrheitstabelle 3.5 für y (KNF)
(durch NAND-Gatter anstelle von AND entsteht y)
y = x1 ∧ x2 ∨ x1 ∧ x2
Hochschule Bremerhaven --- IAE
KV-Diagramm für zwei Variablen
Bild 3.7:
≥1
119
Elektronik und Prozessmesstechnik
27.1
x3 ∨ x2 ∨ x1
1
x2
E K. Müller
Hochschule Bremerhaven --- IAE
gebracht werden. Das Umformen boolscher Gleichungen ist unübersichtlich und führt
folglich nicht mit Sicherheit auf eine minimale Realisierung.
1
0
1
1
1
Markierung zusammenhängender Gebiete im KV-Diagramm
Bei jedem Übergang von einer “Zelle” des KV-Diagramm zur nächten “Zelle” ändert sich
genau eine Variable. Jede “1” entspricht genau einem Minterm.
Ändert sich eine Variable in einem zusammenhängenden Gebiet, so kann die
betreffende Variable aus den Mintermen entfernt werden.
In Bild 3.8 ändert sich die Variable x2 in dem zusammenhängenden Gebiet; folglich kann
sie bei der Realisierung entfallen
y = x1 .
(3.31)
Bei zwei Variablen lohnt sich das Zeichnen des KV-Diagramms meist nicht. Dies ändert
sich bei 3 oder 4 Variablen. Eine größere Anzahl von Variablen würde dreidimensionale
KV-Diagramme erfordern, die sich nicht mehr einfach zeichnen lassen.
27.2
(3.30)
x1 0
KV-Diagramm für drei Variablen
Das KV-Diagramm für drei Variablen erschient etwas unmotiviert. Es muss jedoch eine
Form gefunden werden, bei der vom Übergang von einer Zelle zur benachbarten Zelle sich
jeweils nur eine Variable ändert
E K. Müller
120
Elektronik und Prozessmesstechnik
x3
0
0
0
0
1
1
1
1
Bild 3.9:
x2
0
0
1
1
0
0
1
1
x1
x2 x1
00
y
0
1
0
1
0
1
0
1
E K. Müller
Hochschule Bremerhaven --- IAE
11
01
0
1
1
1
1
1
x3
0
1
0
1
0
1
0
1
10
x1 = 1
x2 = 1
Wahrheitstabelle und zugehöriges Karnaugh-Diagramm für die Variablen x1,
x2 und x3
In Bild 3.9 erkennt man ein zusammenhängendes Gebiet aus vier Einsen. Dieses Gebiet
ist in Bild 3.10 markiert.
x2 x1
00
11
01
0
1
1
1
1
1
x3
10
x3
x2
x1
y
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
0
0
0
1
0
1
0
0
0
0
1
1
1
1
Hochschule Bremerhaven --- IAE
x4 x3
x2 x1
00
01
11
1
00
01
1
1
11
1
1
10
10
1
x1 = 1
x2 = 1
x3 = 1
x4 = 1
Wahrheitstabelle und zugehöriges Karnaugh-Diagramm für die Variablen x1,
x2, x2 und x4
In Bild 3.11 sind die zusammenhängenden Gebiete markiert. Da es nur zwei
zusammenhängende Gebiete gibt, lässt sich die logische Schaltung von ursprünglich 6
Mintermen (s. Wahrheitstabelle, 6 Einsen) auf 2 Minterme (Gebiete) reduzieren, was einer
dramatischen Vereinfachung entspricht.
Das senkrecht markierte Gebiet beschreibt den Minterm
Markierung eines zusammenhängenden Gebiets
Es ändern sich die Variablen x2 und x3. Folglich brauchen diese Variablen auch nicht
berücksichtigt werden; es gilt
y = x1 .
x4
Bild 3.11:
x1 = 1
x2 = 1
Bild 3.10:
121
Elektronik und Prozessmesstechnik
(3.32)
(Nachweis z.B. anhand der Wahrheitstabelle.)
y1 = x3 ∧ x4 ,
(3.33)
da sich die Variablen x1 und x2 ändern. Entsprechend folgt für das quadratische Gebiet
(hier ändern sich die Variablen x2 und x4)
y2 = x1 ∧ x3 .
(3.34)
Die Disjunktion (OR) der Minterme beschreibt vollständig die logische Funktion
27.3
KV-Diagramm für vier Variablen
Logische Funktionen mit mehr als vier Variablen lassen sich in einem KV-Diagramm nicht
mehr darstellen. Auch hier muss eine Form gefunden werden, bei der beim Übergang von
einer Zelle zur nächsten Zelle sich nur jeweils eine Variable ändert. Eine mögliche
Realisierung mit einem Beispiel zeigt das Bild 3.11.
y = y1 ∨ y2 = x3 ∧ x4 ∨ x1 ∧ x3 .
(3.35)
Intuitiv findet man diese Lösung im allgemeinen nicht.
Zusammenhängende Gebiete finden
Karnaugh-Diagramms” hinweg.
sich auch
“über die
Grenzen der
E K. Müller
122
Elektronik und Prozessmesstechnik
Hochschule Bremerhaven --- IAE
28
Beispiel
x4
x3
x2
x1
y
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
0
0
0
0
1
0
1
0
0
0
0
Bild 3.12:
Elektronik und Prozessmesstechnik
x4 x3
x2 x1
00
01
11
10
00
01
1
1
11
1
1
x1 = 1
x2 = 1
10
x3 = 1
x4 = 1
123
Literatur
[1]
Bronstein-Semendjajew: Taschenbuch der Mathematik.
Harri Deutsch, 2002
[2]
Tietze, U. und Ch. Schenk: Halbleiter---Schaltungstechnik.
Springer, 2001
[3]
Nührmann, D.: Das komplette Werkbuch Elektronik.
Francis’, 2002
[4]
Lindner, H., H Brauer und C. Lehmann: Taschenbuch der Elektrotechnik und
Elektronik.
Fachbuchverlag Leipzig, 1999
Beispiel zur Auffindung zusammenhängender Gebiete
Die markierten Bereiche bilden ein zusammenhängendes Gebiet im Sinne der
Minimierung von Mintermen, da sich auch beim dem übergang vom rechten zum linken
Rand nur ein Bit ändert. Da es sich also nur um ein zusammenhängendes Gebiet handelt,
wird die logische Funktion also auch nur durch einen einzigen Minterm beschrieben
y = x1 ∧ x3
(3.36)
(es ändern sich in dem Gebiet ja die Variablen x2 und x4). Die logische Funktion der
Wahrheitstabelle nach Bild 3.12 kann also durch die folgende einfache Schaltung
verwirklicht werden:
x1
x3
Bild 3.13:
&
1
y
Schaltungstechnische Realisierung
Die gleichen Zusammenhänge gelten natürlich auch für den oberen und unteren Rand
eines KV-Diagramms.
:::
Hochschule Bremerhaven --- IAE
:::