Gruppe A Bitte tragen Sie SOFORT und LESERLICH Namen

Gruppe A
Bitte tragen Sie SOFORT und LESERLICH Namen und Matrikelnr. ein, und legen Sie Ihren Studentenausweis
bereit.
PRÜFUNG AUS DATENMODELLIERUNG (184.685) GRUPPE A
Matrikelnr.
Familienname
03.05.2016
Vorname
Arbeitszeit: 60 Minuten. Lösen Sie die Aufgaben auf den vorgesehenen Blättern; Lösungen auf Zusatzblättern
werden nicht gewertet. Viel Erfolg!
Aufgabe 1:
(6)
a) Bestimmen Sie für die folgenden Relationenschemata (R, F1 ) und (R, F2 ) mit R = ABCDEFG, sämtliche
Schlüssel.
Abhängigkeiten
Schlüssel
F1 = {F → AB , BE → G, D → B , GF → CD, DB → EF }
........................
F2 = {EA → BG, C → ABD, F → BEG, AG → BC }
........................
b) Geben Sie für die folgenden Relationenschemata (R, F1 ) und (R, F2 ) mit R = ABCDEF GH, an, welche
Normalformen sie erfüllen, indem Sie die richtigen Antworten ankreuzen.
Achtung: pro korrekter Lösung: 1 Punkt, pro falscher Lösung -1 Punkt, pro nicht beantworteter Frage 0 Punkte,
insgesamt mindestens 0 Punkte.
Abhängigkeiten
Schlüssel
F1 ={CEF → ADF , DC → B , ABC → GEF , D → BCD, EF → ADH }
EF, ABC, AD
keine Normalform
BCNF & nicht 3NF
3NF & nicht BCNF 3NF & BCNF F2 ={ADE → BFC , BD → CEH , CGH → CH , BF → AD, DE → AG}
keine Normalform
BCNF & nicht 3NF
DE, BF, DB
3NF & nicht BCNF 3NF & BCNF Aufgabe 2:
(6)
Gegeben sind die Relationen R(KLM ) mit 7 Tupeln, S(LN O) mit 5 Tupeln und T (K N ) mit 6 Tupeln.
Geben Sie die minimale bzw. maximale Größe (= Anzahl der Tupel) der durch die folgenden Ausdrücke entstehenden Relationen an:
Ausdruck
min. Ergebnisgröße
max. Ergebnisgröße
πN (T ) − πN (S)
(S (S × T ))
πKLM (σK=25∨L=14 (R S))
............
............
............
............
............
............
Aufgabe 3:
(8)
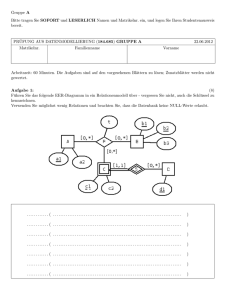
Führen Sie das folgende EER-Diagramm in ein Relationenmodell über. Markieren Sie pro Relation einen Schlüssel
durch unterstreichen der entsprechenden Attribute. Kennzeichnen Sie Fremdschlüssel durch das Voranstellen des
Namens der Relation, auf die sich der Schlüssel bezieht – also als Relation.Attribut.
Verwenden Sie möglichst wenig Relationen und beachten Sie, dass die Datenbank keine NULL-Werte erlaubt.
h2
f2
j3
f3
f1
(0,1)
j1
(1,1)
i
J
h1
(0,1)
F
(1,1)
H
g
j2
(0,1)
M
(3,5)
n
............ ( .......................................................................
)
............ ( .......................................................................
)
............ ( .......................................................................
)
............ ( .......................................................................
)
............ ( .......................................................................
)
............ ( .......................................................................
)
............ ( .......................................................................
)
............ ( .......................................................................
)
............ ( .......................................................................
)
Aufgabe 4:
(6)
a) Betrachten Sie die beiden Mengen Fd und Fd0 von funktionalen Abhängigkeiten (FDs) über dem Schema R =
ABCD.
Fd = {A → B , AC → D}
Fd0 = {A → B , BC → D}
Sind diese beiden Mengen von funktionalen Abhängigkeiten äquivalent (also gilt Fd ≡ Fd0 )? Falls ja, geben Sie
eine formale Begründung. Falls nein, geben Sie bitte ein Gegenbeispiel (also eine Ausprägung für R welche eine
der beiden Mengen an FDs erfüllt, die andere jedoch nicht; geben Sie außerdem an welche FD nicht erfüllt wird).
Achtung: Ankreuzen alleine gibt keine Punkte – Punkte gibt es nur für die Begründung.
Fd ≡ Fd0 ?
ja nein b) Betrachten sie das Schema (R, F ) mit R = ABCDE und F = {A → B , B → D, B → C , BC → E }.
Geben Sie drei Funktionale Abhängigkeiten an, welche sich mittels den Armstrong Axiomen der Transitivität,
Pseudotransitivität und Vereinigung aus F ableiten lassen. Geben Sie jeweils an welches Armstrong Axiom Sie
verwenden, sowie auf welche beiden Funktionalen Abhängigkeiten Sie dieses anwenden (ein Beispiel wie die Antwort
aussehen sollte ist unten angegeben). Sie können neben den Funktionalen Abhängigkeiten in F auch jene verwenden
die bereits in einem früheren Schritt abgeleitet wurden. Sie dürfen das selbe Axiom auch öfters (auf anderen FDs)
verwenden. Es müssen nicht alle drei Axiome verwendet werden.
Armstrong Axiom
Transitivität
angewandt auf
A → B, B → D
Ergebnis
A→D
..................................
............................
......................
..................................
............................
......................
..................................
............................
......................
Aufgabe 5:
(5)
Gegeben ist ein Relationenschema CDEFGHI und die Menge Fd von funktionalen Abhängigkeiten. Bestimmen
Sie die kanonische Überdeckung.
Fd = {D → H , CF → H , I → EG, CF → EF , DE → CI , EG → CD, H → GDE }
Fc =
n
o
Aufgabe 6:
(6)
Einige Ihrer Erkenntnisse aus der Recherche zu verlässlichen Schreibgeräten haben Sie in folgenden Relationen
gespeichert (kursiv geschriebene Attribute kennzeichnen Fremdschlüssel, Unterstreichungen Primärschlüssel):
Hersteller(mname, gründung, land)
Modell(mname, nummer, preis)
Kategorie(name, beschreibung, gewichtung)
Bewertung(mname, nummer, name, score)
a) Gesucht ist eine Liste (mname, nummer, name) aller Paare von Modellen und Kategorien für die noch keine
Bewertung vorliegt – also welche Modelle noch in welchen Kategorien bewertet werden müssen. Formulieren Sie
diese Anfrage in der relationalen Algebra.
b) Gegeben sind folgende Anfragen in der relationalen Algebra:
q1 : ρmname←Modell.mname,nummer←Modell.nummer (
πModell.mname,Modell.nummer,preis (σModell.nummer>1∧score>3 (σModell.nummer=Bewertung.nummer (Modell×Bewertung))))
q2 : πmname,nummer,preis (σnummer>1 (Modell
Bewertung) ∩ σscore>3 (Modell
Bewertung))
Geben Sie eine Ausprägung für die Relationen Modell und Bewertung an, so dass q1 und q2 , ausgewertet auf diesen
Ausprägungen, unterschiedliche Ergebnisse liefern. Geben Sie außerdem ein Tupel (mname, nummer, preis) an,
welches auf der von Ihnen gewählten Ausprägung eine Lösung von q1 aber nicht von q2 ist.
Hinweis: Sie können als Werte einfache Zahlen oder Buchstaben – 1,2,3,4, . . . , a,b,c, . . . – verwenden, und
brauchen keine “sinnvollen” Einträge angeben. Auch brauchen Sie sich keine Gedanken um sinnvolle Datentypen
machen – d.h. auch “name” darf 1 sein oder “nummer” a.
Wenn Sie ein Gegenbeispiel mit weniger als 2 Tupeln pro Relation finden, brauchen Sie die zweite Zeile nicht
ausfüllen, sonden können sie einfach leer lassen.
Modell
mname
Bewertung
nummer
preis
mname
nummer
name
score
Tupel: . . . . . . . . . . . . . . . . . . . . . . . . . . . .
c) Gegeben sind die folgenden Ausprägungen für drei der Relationen.
Modell
Kategorie
mname
nummer
preis
name
beschreibung
gewichtung
Schreiberling
1
48,95
Handling
[...]
8
Schreiberling
2
75,95
Haptik
[...]
5
Fehlerfrei
5
17,01
Verarbeitung
[...]
6
Tintenklecks
2
154,99
Haltbarkeit
[...]
7
Papierverzier
1
68,95
Genauigkeit
[...]
9
Bewertung
mname
nummer
name
score
Schreiberling
1
Haptik
4
Schreiberling
1
Verarbeitung
3
Tintenklecks
2
Handling
1
Tintenklecks
2
Genauigkeit
0
Schreiberling
1
Haltbarkeit
7
Fehlerfrei
5
Handling
9
Fehlerfrei
5
Genauigkeit
10
Papierverzier
1
Haptik
6
Papierverzier
1
Genauigkeit
7
Des weiteren ist folgendes ER-Diagramm gegeben, welches die drei Relationen beschreibt. Geben Sie für die Beziehung “Bewertung” die genauesten Werte in der (min,max)-Notation an, so dass die oben angegeben Ausprägungen
diese Werte erfüllen (d.h. die größtmöglichen Werte für “min”, und die kleinstmöglichen Werte für “max”.
Modell
Bewertung
Kategorie
Aufgabe 7:
Die Angabe zu dieser Aufgabe befindet sich auf der nächsten Seite.
(8)
Gesamtpunkte: 45
Sie können diese Seite abtrennen und brauchen sie nicht abzugeben!
Diesen Zettel daher bitte nicht beschriften! (Lösungen auf diesem Zettel werden nicht gewertet!)
Angabe für Aufgabe 7:
Ein zuverlässiges Schreibgerät das einen auch in den schwierigsten Extremsituationen nicht im Stich lässt ist
das wichtigste technische Hilfsmittel bei Prüfungen. Während Sie sich im Zuge Ihrer akribischen Vorbereitung auf
diese Prüfung deshalb einige Produktionsstätten von Kugelschreibern angesehen haben, entschied man sich in einer
davon auf Grund Ihrer Fragen ein neues Systems zur Qualitätssicherung zu implementieren und bat um Ihre Hilfe.
Zeichnen Sie aufgrund der vorliegenden Informationen ein EER-Diagramm. Verwenden Sie dabei die (min,max)
Notation. Es sind keine NULL-Werte erlaubt, und Redundanzen sollen vermieden werden.
Jedes (Kugelschreiber) Modell trägt eine eindeutige Bezeichnung (BEZ), besitzt einen Preis (PREIS), und wurde
von einem Kugelschreiberdesigner (DESIGNER) entworfen. Jeder produzierte Kugelschreiber ist eindeutig identifiziert durch das Modell, eine Fließbandnummer (FNR) und eine Laufnummer (LNR). Außerdem wird zu jedem
Kugelschreiber die Farbe vermerkt (FARBE).
Mitarbeiter können durch ihre Sozialversicherungsnummer (SVNR) zusammen mit ihrem Gehalt (GEHALT) eindeutig identifiziert werden. Des weiteren ist zu jedem Mitarbeiter eine email Adresse bekannt (EMAIL). Es soll
gespeichert werden welcher Mitarbeiter welchen Kugelschreiber zusammengebaut hat, wobei jeder Kugelschreiber
von genau einem Mitarbeiter zusammengebaut wird.
Prüfmethoden zum Testen der Qualität von Kugelschreibern haben einen eindeutigen Namen (NAME), und
darüber hinaus eine eindeutige ISO-Nummer (ISONR). Des weiteren verursacht jede Prüfmethode gewisse Kosten
(KOSTEN). Es soll nun gespeichert werden, welcher Kugelschreiber von welchem Mitarbeiter mittels welcher
Prüfmethode geprüft wurde. Dabei wird jeder Kugelschreiber mindestens zwei mal geprüft – aus Kostengründen
jedoch nicht öfter als fünf mal. Jeder Mitarbeiter muss mindestens fünf Überprüfungen vorgenommen haben.
Prüfmethoden können beliebig oft zum Einsatz kommen, wobei nicht jede Methode auch angewendet werden
muss.
Jede Bestellung ist eindeutig identifiziert durch eine Bestellnummer (BID). Zusätzlich soll eine Kreditkartennummer (KNR) und eine Versandadresse (ADRESSE) gespeichert werden. Eine Bestellung kann mehrere Kugelschreibermodelle beinhalten, mindestens jedoch eines. Für jedes bestellte Modell soll die Menge (MENGE) der bestellten
Exemplare vermerkt werden.
Wurde eine Bestellung bearbeitet wird das Datum der Fertigstellung vermerkt (DATUM). Außerdem wird gespeichert mit welchen Kugelschreibern die Bestellung erfüllt wurde. Jeder bearbeiteten Bestellung muss mindestens
ein Kugelschreiber zugewiesen sein. Ein Kugelschreiber kann maximal einer solchen Bestellung zugewiesen sein.