Prüfung Physik IA 2016-04-27

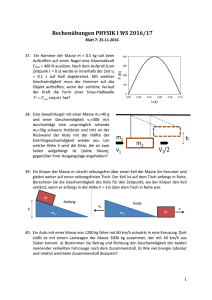
Rechenteil: Physik IA, 27.04.2016 (Maximal 12 Punkte) 1. Ein Ball wird mit einer Geschwindigkeit von 10 m/s nach oben geschossen. Gleichzeitig wird von jener Höhe, die dieser Ball maximal erreichen würde, ein zweiter Ball mit der Geschwindigkeit von 2 m/s nach unten geworfen. Zu welchem Zeitpunkt nach dem Start, in welcher Höhe über dem Boden und mit welchen Geschwindigkeiten stoßen die beiden Bälle aufeinander? (4 Punkte) 2. Gegeben sei eine homogene Kreisscheibe mit Radius R = 30 cm. Die Scheibe wird exzentrisch um eine horizontale Achse gelagert. Diese Drehachse (AP) hat einen Abstand von 20 cm vom Schwerpunkt (SP) der Scheibe und steht senkrecht auf diese. Die Scheibe AP
wird nun aus ihrer Ruhelage soweit um die Drehachse AP gedreht, bis sich der Schwerpunkt auf SP
gleicher Höhe mit der Drehachse befindet, und dann losgelassen. Mit welcher Geschwindigkeit bewegt sich der tiefste Punkt der Scheibe durch seine Ruhelage? (4 Punkte). 3. Ein Mann hält einen Gartenschlauch von 5 cm2 Innenquerschnitt mit einer Durchflussrate von 7.5 Liter Wasser pro Minute. Zwischen Schlauch und Auslassdüse ergibt sich ein Druckabfall von 2 bar. Welchen Durchmesser hat die Austrittsöffnung der Düse? (Annahme ideale inkompressible Flüssigkeit ohne Reibung). (4 Punkte) Theoretischer Teil: Physik IA, 27.04.2016 (2 Fragen nach Wahl beantworten, maximal 8 Punkte) 1. Ein Körper der Masse m rutscht über einen Keil der Masse mK = 4m herunter und gleitet weiter auf einen reibungsfreien Tisch. Der Keil ist auf dem Tisch anfangs in Ruhe. Berechnen Sie die Geschwindigkeit des Keils für den Zeitpunkt, wo der Körper den Keil verlässt, wenn er anfangs in der Höhe h über dem Tisch in Ruhe war. (4 Punkte) Anfang
h
mK
Ende
vK
mK
m
v
2. Eine ungedämpfte harmonische Federpendelschwingung mit einer Eigenfrequenz f hat zum Zeitpunkt t = 0 eine Auslenkung von x0 und eine Geschwindigkeit v0. Bestimmen Sie allgemein die Maximalamplitude A und die Anfangsphase  der Schwingung x(t) = A sin(t + ) als Funktion von x0, v0 und . Was bedeuten die beiden Spezialfälle  = 0 und /2 ? (4 Punkte) 3. Das dritte Keplersche Gesetz lautet: Die Quadrate der Umlaufzeiten zweier Planeten um eine Sonne verhalten sich wie die dritten Potenzen (Kuben) der großen Bahnhalbachsen. Beweisen Sie dieses Gesetz für kreisförmige Umlaufbahnen unter Zuhilfenahme des Gravitationsgesetzes. Wie würde das dritte Keplersche Gesetz für ein Zentralkraftfeld der Form F = k/r lauten, wobei k eine Konstante und r der Betrag des Abstandsvektors ist. (4 Punkte)