m v m V /2 h

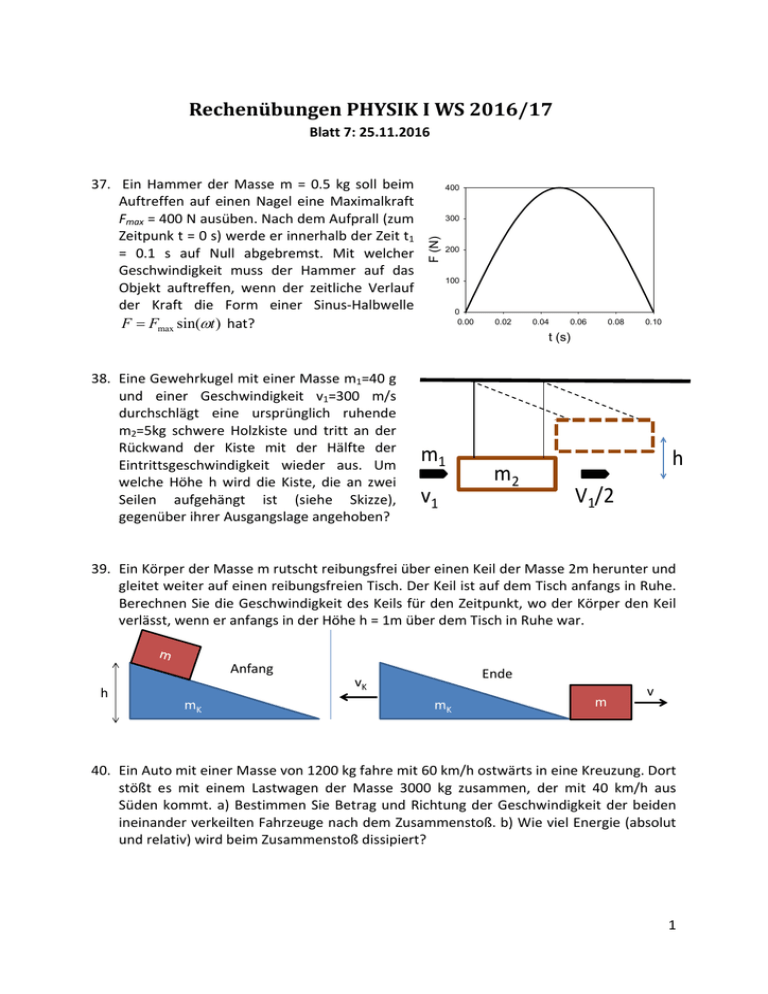
 RechenübungenPHYSIKIWS2016/17
F (N)
Blatt 7: 25.11.2016 37. Ein Hammer der Masse m = 0.5 kg soll beim 400
Auftreffen auf einen Nagel eine Maximalkraft 300
Fmax = 400 N ausüben. Nach dem Aufprall (zum Zeitpunk t = 0 s) werde er innerhalb der Zeit t1 200
= 0.1 s auf Null abgebremst. Mit welcher Geschwindigkeit muss der Hammer auf das 100
Objekt auftreffen, wenn der zeitliche Verlauf der Kraft die Form einer Sinus‐Halbwelle 0
0.00
0.02
0.04
0.06
0.08
0.10
F  Fmax sin(t ) hat? t (s)
38. Eine Gewehrkugel mit einer Masse m1=40 g und einer Geschwindigkeit v1=300 m/s durchschlägt eine ursprünglich ruhende m2=5kg schwere Holzkiste und tritt an der Rückwand der Kiste mit der Hälfte der m1
h
Eintrittsgeschwindigkeit wieder aus. Um m
2
welche Höhe h wird die Kiste, die an zwei V1/2
Seilen aufgehängt ist (siehe Skizze), v1
gegenüber ihrer Ausgangslage angehoben? 39. Ein Körper der Masse m rutscht reibungsfrei über einen Keil der Masse 2m herunter und gleitet weiter auf einen reibungsfreien Tisch. Der Keil ist auf dem Tisch anfangs in Ruhe. Berechnen Sie die Geschwindigkeit des Keils für den Zeitpunkt, wo der Körper den Keil verlässt, wenn er anfangs in der Höhe h = 1m über dem Tisch in Ruhe war. Anfang
h
Ende
vK
mK
mK
m
v
40. Ein Auto mit einer Masse von 1200 kg fahre mit 60 km/h ostwärts in eine Kreuzung. Dort stößt es mit einem Lastwagen der Masse 3000 kg zusammen, der mit 40 km/h aus Süden kommt. a) Bestimmen Sie Betrag und Richtung der Geschwindigkeit der beiden ineinander verkeilten Fahrzeuge nach dem Zusammenstoß. b) Wie viel Energie (absolut und relativ) wird beim Zusammenstoß dissipiert? 1 41. Ein Fahrrad bremst über einen Weg von 115 m gleichmäßig von v0 = 8.4 m/s ab, bis es zum Stehen kommt. Jedes Rad hat einen Gesamtdurchmesser von 68 cm. Bestimmen Sie a) die Winkelgeschwindigkeit der Räder zum Anfangszeitpunkt, b) die Gesamtzahl der Umdrehungen, die jedes Rad macht bevor es zum Stehen kommt, c) die Winkelbeschleunigung des Rades und d) die Zeit die es benötigt um zum Stehen zu kommen. 42. An den Eckpunkten eines gleichseitigen Dreiecks mit einer Seitenlänge von s = 40 cm befinden sich jeweils gleiche punktförmige Massen mit m = 0.5 kg. Dieses Dreieck wird um eine senkrecht auf die Dreiecksfläche stehende Drehachse in Rotation versetzt. Berechnen Sie die in dieser Rotation gespeicherte kinetische Energie bei einer Rotationsgeschwindigkeit von 10 Umdrehungen pro Sekunde, wenn a) die Drehachse durch den Schwerpunkt des Dreiecks geht und b) die Drehachse durch einen der Massen an den Eckpunkten geht. 2