6te Serie_WS2013_tonisch

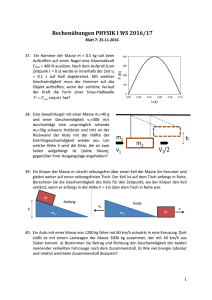
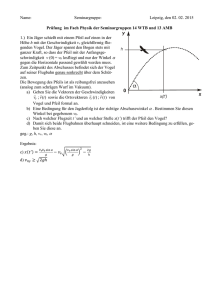
Technische Universität Ilmenau
Fakultät für Mathematik und Naturwissenschaften
Institut für Physik
http://www.tu-ilmenau.de/techphys2/lehre/
Übungen zur Vorlesung Physik I für Ingenieursstudiengänge im WS 2013
06. Serie: Schein- und Reibungskräfte
Aufgabe 21:
Für ein Belastungsexperiment rotiert ein Motor (z.B. ein Boxermotor) mit einer
Winkelgeschwindigkeit ω = 4 s-1 in einem Abstand von r = 2,5 m um die Drehachse A. Die
Kolbenbewegung verläuft in horizontaler Ebene und steht senkrecht zur Bahnkurve des Motors. Die
Masse eines Kolbens ist 0,7 kg.
r
r
a) Welche Bahngeschwindigkeit besitzt der Schwerpunkt S des Motors?
b) Die maximale Geschwindigkeit v‘ eines Kolbens im Motor ist 1 cm je Millisekunde. Wie groß
ist die CORIOLIS-Kraft auf die Wand des Zylinders?
c) Welche Richtung hat die CORIOLIS-Kraft, wenn der linke Kolben sich mit der Geschwindigkeit
v‘ momentan in Richtung der Drehachse A bewegt?
Aufgabe 22:
Eine Testrakete mit der Startmasse m = 600 kg bewegt sich mit einer konstanten Geschwindigkeit
von v0‘ =400 m/s durch eine geregelte Schubkraft bei der geographischen Breite β = 51° lotrecht nach
oben.
a) Man berechne daraus die CORIOLIS-Kraft und die CORIOLIS-Beschleunigung! In welche
Richtung ist die Kraft gerichtet?
b) Wie groß ist näherungsweise die durch die CORIOLIS-Beschleunigung hervorgerufene
Abweichung nach t = 5 s?
Der Brennstoffverlust während der Zeit von 5 s soll bei den Rechnungen keine Berücksichtigung
finden!
Aufgabe 23:
Ein Lastwagen (Masse 2,2 t) hat eine Spurbreite von 2,2 m sein Schwerpunkt ohne Ladung liegt bei
einer Höhe von z = 1,4 m. Der Haftreibungskoeffizient zwischen Straße und Reifen (Gummi/Asphalt
feucht) beträgt µH = 0,73.
a) Mit welcher Geschwindigkeit darf der LKW eine nicht überhöhte Kurve mit dem Radius
r = 100 m durchfahren, damit er nicht rutscht?
b) Liegt die resultierende Kraft aus der Normalkraft und der Zentrifugalkraft innerhalb oder
außerhalb der Spurbreite? Erstellen Sie eine Skizze! Wie groß ist der Betrag der
resultierenden Kraft?
Aufgabe 24:
In einer horizontalen Führung (v senkrecht auf g) bewegt sich ein Zylinder mit der Masse M = 10 kg
unter dem Einfluss einer Seilkraft, die über eine Umlenkrolle durch die Gewichtskraft eines zweiten
Körpers mit der Masse m = 3 kg wirkt, von einem Bereich mit der Gleitreibungszahl µG = 0,03 in
einem Bereich mit µG = 0,23 (siehe Skizze). Rollen- und Fadenmasse können vernachlässigt werden.
a) Berechnen sie für beide Gleitreibungsbereiche die Beschleunigung für beide Körper!
b) Aus der Kräftebilanz ist die Seilkraft (Formel) zu ermitteln und für beide Bereiche die jeweils
auftretende zu berechnen.
c) Wie groß ist die Seilkraftdifferenz beim Übergang in die unterschiedlichen Bereiche?
(Lösung 4,6 N)