Blatt 6

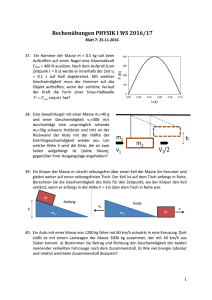
 RechenübungenPHYSIKIWS2013/14
Blatt 6: 22.11.2013 31. Ein Fahrrad bremst über einen Weg von 115 m gleichmäßig von v0 = 8.4 m/s ab, bis es zum Stehen kommt. Jedes Rad hat einen Gesamtdurchmesser von 68 cm. Bestimmen Sie a) die Winkelgeschwindigkeit der Räder zum Anfangszeitpunkt, b) die Gesamtzahl der Umdrehungen, die jedes Rad macht bevor es zum Stehen kommt, c) die Winkelbeschleunigung des Rades und d) die Zeit die es benötigt um zum Stehen zu kommen. 32. An den Eckpunkten eines gleichseitigen Dreiecks mit einer Seitenlänge von s = 40 cm befinden sich jeweils gleiche punktförmige Massen mit m = 0.5 kg. Dieses Dreieck wird um eine senkrecht auf die Dreiecksfläche stehende Drehachse in Rotation versetzt. Berechnen Sie die in dieser Rotation gespeicherte kinetische Energie bei einer Rotationsgeschwindigkeit von 10 Umdrehungen pro Sekunde, wenn a) die Drehachse durch den Schwerpunkt geht und b) die Drehachse durch einen der Massen an den Eckpunkten geht. 33. Berechnen Sie den vektoriellen Drehimpuls bezüglich des Ursprungs für folgende drei Fälle: a) ein Auto mit der Masse m = 1200 kg fährt mit einer Geschwindigkeit von v = 15 m/s auf einer Kreisbahn mit Radius r = 20 m in der x‐y Ebene gegen den Uhrzeigersinn um den Ursprung. b) dasselbe Auto bewegt sich in der x‐y Ebene mit einer Geschwindigkeit von v x = -15m/s auf einer geradlinigen Bahn mit y = y0 = 20 m parallel zur x‐Achse. c) Eine Scheibe mit homogener Dichte mit Radius r0 = 20 m und Masse m = 1200 kg rotiert mit ω = 0.75 s‐1 in der x‐y Ebene im Uhrzeigersinn um die z‐Achse. 34. Zwei Blöcke mit Massen m1 = 4 kg und m2 = 2 kg sind jeweils frei hängend über eine Umlenkrolle mit einem Seil verbunden. Die Umlenkrolle ist ein homogener Vollzylinders mit Masse M = 2 kg und Radius R = 20 cm. Das als masselose angenommene Seil laufe schlupffrei (reine Rollbewegung) und die Lagerung sei reibungsfrei. a) wie groß ist die lineare Beschleunigung der beiden Blöcke? b) Wie groß ist die Winkelbeschleunigung der Rolle? c) Wie groß sind die beiden Seilkräfte links und rechts der Umlenkrolle? D
35. Gegeben Sei eine masselose feste Stange der Länge L = 2 m, die an einem Ende am Punkt D drehbar aufgehängt ist und an deren anderem Ende eine Punktmasse mit m1 = 2 kg m2=3kg
α=450
hängt. Eine weitere Masse m2 = 3 kg ist 50 cm vom Ende m1=2kg
entfernt montiert (siehe Skizze). a) Die Stange wird aus der Ruhelage um den Winkel 450 ausgelenkt und dann v2=?
losgelassen. Mit welcher Geschwindigkeit bewegen sich v1=?
beide Massen durch den tiefsten Punkt? 36. Ein homogener dünner Stab der Länge l = 1 m kann frei um eine Achse senkrecht zur Stabachse rotieren. Finden Sie die Schwingungsdauer für kleine Auslenkungen wenn der Stab a) am Stabende aufgehängt ist, und b) 0.25 m vom Stabende entfernt aufgehängt ist. 1