Prüfung Physik IA 2014-12-10

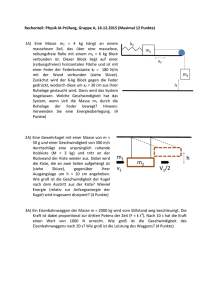
Rechenteil: Physik IA Prüfung, 10.12.2014 (Maximal 12 Punkte) 1. 1A) In einem Windkanal wird ein Tragflächenmodell mit einer Masse m = 500 kg und einer Fläche A = 10 m2 von Luft (Dichte  = 1.2 kg/m3) mit der Geschwindigkeit v0 = 40 m/s angeströmt. Oberhalb der Tragfläche hat die Luft die Geschwindigkeit v0+v, unterhalb v0‐v. Wie groß muss v sein, damit der Strömungsauftrieb durch den Venturi Effekt gerade der Gewichtskraft der Tragfläche entspricht? (4 Punkte) 2. 1B) Ein Mann hält einen Gartenschlauch von 5 cm2 Innenquerschnitt mit einer Durchflussrate von 7.5 Liter Wasser pro Minute. Zwischen Schlauch und Auslassdüse ergibt sich ein Druckabfall von 2 bar. Welchen Durchmesser hat die Austrittsöffnung der Düse? (4 Punkte) 3. 2A) Eine Masse m2 = 4 kg hängt an einem masselosen Seil, das über eine masselose, reibungsfreie Rolle mit einem m1 = 6 kg Block verbunden ist. Dieser Block liegt auf einer (reibungsfreien) horizontalen Fläche und ist mit einer Feder der Federkonstante kF = 180 N/m mit der Wand verbunden (siehe Skizze). Zunächst wird der 6‐kg Block gegen die Feder gedrückt, wodurch diese um xF = 30 cm aus ihrer Ruhelage gestaucht wird. Dann wird das System losgelassen. Welche Geschwindigkeit hat das System, nachdem die Masse m2 um h = 30 cm nach unten gesunken ist? (4 Punkte) 4. 2B) Eine Gewehrkugel mit einer Masse von 50 g und einer Geschwindigkeit von 200 m/s durchschlägt eine ursprünglich ruhende 5 kg schwere Holzkiste und tritt an der Rückwand der Kiste mit der Hälfte m1
h
der Eintrittsgeschwindigkeit wieder aus. m
2
Um welche Höhe h wird die Kiste, die an V1/2
v
1
zwei Seilen aufgehängt ist (siehe Skizze), gegenüber ihrer Ausgangslage angehoben? (4 Punkte) 5. 3A) Gegeben Sei eine masselose feste Stange der Länge L = 2 m, die an einem Ende am Punkt D drehbar aufgehängt ist und an deren anderem Ende eine Punktmasse mit m1 = 2 kg hängt. Eine weitere Masse m2 = 3 kg ist 50 cm vom Ende entfernt montiert (siehe Skizze). a) Die Stange wird aus der Ruhelage um den Winkel 450 ausgelenkt und dann losgelassen. Mit welcher Geschwindigkeit bewegen sich beide Massen durch den tiefsten Punkt? (4 Punkte) D
=450
m2=3kg
m1=2kg
v2=?
v1=?
6. 3B) Zwei homogene Kreisscheiben mit unterschiedlichem Radius (R1 = 30cm, R2 = 26cm) aber gleicher Masse (M = 2kg) sind am Umfang miteinander starr verbunden (siehe Skizze). Durch den Verbindungspunkt geht eine horizontale masselose Drehachse (senkrecht zur Zeichenebene in der Skizze). Am Beginn sei die Anordnung, wie gezeichnet, in horizontaler Ausgangslage. Wird die Drehung freigegeben, dann kippt die große Scheibe nach unten. Berechnen Sie die Geschwindigkeit, mit der sich der Mittelpunkt der großen Scheibe durch den tiefsten Punkt bewegt. (4 Punkte) Theoretischer Teil: Physik IA Prüfung, 10.12.2014 (2 Fragen nach Wahl beantworten, maximal 8 Punkte) 1. 1A) Sind der Impuls und der Drehimpuls eines Himmelskörpers bei seiner Rotation um ein Zentralgestirn (z.B. Erde um die Sonne) erhalten? Belegen Sie Ihre Argumentation mit einer quantitativen Berechnung. (4 Punkte). 2. 1B) Zeigen Sie, dass die Gesamtenergie eines Satelliten auf einer Kreisbahn um die Erde genau die Hälfte seiner potentiellen Energie ist. Hinweis: die potentielle Energie einer Masse im Gravitationsfeld ist negativ! (4 Punkte) 3. 2A) Leiten Sie die Differentialgleichung für ein mathematisches Pendel (Punktmasse m, aufgehängt an einem masselosen Faden der Länge L) für kleine Auslenkungen allgemein her. Drücken Sie diese Differentialgleichung durch Größen der Drehbewegung (Winkelbeschleunigung, Trägheitsmoment) aus, und diskutieren Sie die Erweiterung auf nicht‐punktförmige Körper, die außerhalb Ihres Schwerpunktes aufgehängt sind (physikalisches Pendel). Berechnen Sie allgemein die Schwingungsfrequenz für ein physikalisches Pendel als Funktion des Abstandes des Drehpunktes vom Schwerpunkt. (4 Punkte) 4. 2B) Ein mathematisches Pendel (Punktmasse m, aufgehängt an einem masselosen Faden der Länge L) werde um einen Winkel 0 ausgelenkt und dann losgelassen. Berechnen Sie die Geschwindigkeit der Masse beim Nulldurchgang 0 auf zwei Arten: a) durch eine Energiebetrachtung, und b) mithilfe der Lösung der Pendeldifferenzialgleichung für kleine Auslenkungen,    0 cos( p t ) , mit der Kreisfrequenz des Pendels  p  g / l . c) Zeigen Sie, dass die beiden Geschwindigkeiten für kleine Auslenkungen identisch sind. (4 Punkte) 5.
6.
3A) a) Wie sind die Dehnung und die Spannung bei einem Zugversuch definiert und wie hängen diese für die meisten Festkörper für kleine Verformungen zusammen? b) Vergleichen Sie diese Beziehung mit der rücktreibenden Kraft einer Feder, und stellen Sie einen Zusammenhang zwischen dem Elastizitätsmodul und der Federkonstanten her. (4 Punkte) 3B) Beschreiben Sie (in Worten und Formeln) die Coulomb‘sche‐, die Stoke’sche‐ und die Newton’sche Reibungskraft. Wo treten diese auf? Was ist der Unterschied zwischen Haftreibung und Gleitreibung, bei welcher der o.g. Reibungskräften spielen diese eine Rolle? c) Formulieren Sie das (dynamische) Kräftegleichgewicht für eine schwingende Feder in einer Flüssigkeit unter Berücksichtigung der entsprechenden Reibungskraft. (4 Punkte)