Prüfung Physik IA 2016-03-02

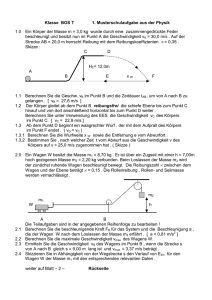
Rechenteil: Physik IA, 02.03.2016 (Maximal 12 Punkte) 1. Zwei Go Karts mit gleicher Masse m = 50 kg veranstalten ein Wettrennen über 100 m. Beide starten zum Zeitpunkt t = 0 s am Ort x = 0 m. Die Kraft auf Wagen 1 ist proportional zum Quadrat der Zeit F1 = k1*t2 und jene auf Wagen 2 ist direkt proportional zur Zeit, F2 = k2*t. Nach 9 Sekunden Fahrzeit ist die Kraft auf die beiden Wagen gleich groß und beträgt 18 N. Nach welcher Zeit haben die beiden Wägen die gleiche Geschwindigkeit? Nach welcher Zeit sind die beiden am gleichen Ort? Welcher Wagen gewinnt das Rennen? (4 Punkte) 2. Ein 80 cm langer Stab der Masse 0.25 kg ist an einem Ende reibungsfrei gelagert. Er wird horizontal gehalten und dann losgelassen. a) Wie groß sind unmittelbar nach dem Loslassen die Beschleunigung eines Punktes am freien Ende des Stabes? b) Berechnen Sie, welche lineare Geschwindigkeit das Stabende hat, wenn es die Vertikale passiert. (4 Punkte) 3. Die Fluchtgeschwindigkeit ist jene Startgeschwindigkeit die ein Körper (z.B. eine Rakete) haben muss, um vollständig aus dem Gravitationsfeld eines Himmelskörpers herauszukommen. a) Berechnen Sie erst allgemein die Fluchtgeschwindigkeit aus einer Energiebetrachtung. b) Auf dem Planeten Vulkan beträgt die Fluchtgeschwindigkeit 11.2 km/s. Die Masse des Vulkan ist 460 mal größer als die des Planeten Gliese 581c, und der Vulkanradius übertrifft den Radius des Gliese um einen Faktor 5.4. Berechnen Sie die Fluchtgeschwindigkeit für einen Körper auf der Glieseoberfläche. (4 Punkte) Theoretischer Teil: Physik IA, 02.03.2016 (2 Fragen nach Wahl beantworten, maximal 8 Punkte) 1. Ein Körper der Masse m rutscht über einen Keil der Masse 2m herunter und gleitet weiter auf einen reibungsfreien Tisch. Der Keil ist auf dem Tisch anfangs in Ruhe. Berechnen Sie die Geschwindigkeit des Keils für den Zeitpunkt, wo der Körper den Keil verlässt, wenn er anfangs in der Höhe h über dem Tisch in Ruhe war. (4 Punkte) Anfang
h
mK
Ende
vK
mK
m
v
2. Beschreiben Sie in Worten den Unterschied zwischen einem mathematischen und einem physikalischen Pendel. Verwenden Sie grundlegende Beziehungen zwischen Größen der Drehbewegung von ausgedehnten Körpern, um eine allgemeine Schwingungsdifferenzialgleichung für ein physikalisches Pendel herzuleiten. Berechnen Sie die Kreisfrequenz dieses Pendels allgemein und für den Spezialfall eines mathematischen Pendels. (4 Punkte) 3. Beschreiben Sie (in Worten und Formeln) die Coulomb‘sche‐, die Stoke’sche‐ und die Newton’sche Reibungskraft. Wo treten diese auf? b) Was ist der Unterschied zwischen Haftreibung und Gleitreibung, bei welcher der o.g. Reibungskräften spielen diese eine Rolle? c) Formulieren Sie das (dynamische) Kräftegleichgewicht für eine schwingende Feder in einer Flüssigkeit unter Berücksichtigung der entsprechenden Reibungskraft. (4 Punkte)