Fortgeschrittenen-Praktikum IIe Astrophysik

Fortgeschrittenen-Praktikum IIe
Astrophysik- und Spektroskopie
Institut für
Theoretische Physik und Astrophysik
der Christian-Albrechts-Universität
zu Kiel
Durchführung und Protokoll:
Phillip Dunzlaff
Aron Gaal
Ali Ismaeil
Inhaltsverzeichnis
Seite 4
1
Einleitung
2
Visuelle Beobachtungen
5
2.1
Das Teleskop
5
2.2
Aufsuchen von Himmelsobjekten
5
2.3
Gesichtsfeldmessung
5
2.3.1
Messungen
6
2.3.2
Ergebnisse und Fehlerabschätzungen
7
2.4
3
4
Bestimmung des Auflösungsvermögens
7
2.4.1
Das Auflösungsvermögen eines Teleskops
7
2.4.2
Messungen
7
2.4.3
Diskussion der Ergebnisse
8
Systemeigenschaften der CCD-Kamera ST-7
9
3.1
Das Funktionsprinzip einer CCD-Kamera
9
3.2
Technische Daten der ST-7
10
3.3
Durchführung des ”Trockenversuchs”
10
3.3.1
Ausleserauschen (”Readout noise”)
10
3.3.2
Dunkelstrom (”Dark current”)
10
3.3.3
Linearität
12
Aufnahmen mit der CCD-Kamera
14
4.1
Schwarz-Weiß-Aufnahmen
14
4.1.1
Bearbeitung der Schwarz-Weiß-Aufnahmen
14
4.1.2
Die Galaxie M 51 (Whirlpool-Galaxy)
14
4.1.3
Die Galaxie NGC 891
16
4.1.4
Die Galaxie M 101 (Pinwheel-Galaxy)
16
4.1.5
Der offene Sternhaufen NGC 654 in der Cassiopeia
17
4.1.6
Der Kugelsternhaufen M 3
18
4.1.7
Der offene Sternhaufen M 52
18
4.1.8
Der Komet C/2003 K4 (Linear)
19
4.2
Farbaufnahmen
20
4.2.1
Bearbeitung der Farbaufnahmen
20
4.2.2
Der Crabnebel M 1
20
2
Inhaltsverzeichnis
4.3
5
7
4.2.3
Der Ringnebel M 57
22
4.2.4
Der planetarische Nebel M 27 im Füchslein
22
4.2.5
Der Planetarische Nebel NGC 6781
23
Hochauflösende Mond- und Planetenaufnahmen
24
4.3.1
Saturn
24
4.3.2
Mond
25
Photometrische Aufgaben
28
5.1
Photometrie von DY-Peg
28
5.1.1
Aufnahme und Bearbeitung
28
5.1.2
Interpretation der Ergebnisse
28
5.2
6
3
Farben-Helligkeitsdiagramm von NGC 654
31
5.2.1
Das Farben-Helligkeits-Diagramm
31
5.2.2
Der offene Sternhaufen NGC 654
31
5.2.3
Aufnahme und Bildverarbeitung von NGC 654
31
5.2.4
Erstellung des Farben-Helligkeits-Diagramms
31
5.2.5
Interpretation des Farben-Helligkeits-Diagramms
32
Aufnahme von Sternspektren
34
6.1
Der Spektrograph
34
6.2
Sequenz der Spektraltypen von O bis M
35
6.2.1
Die Spektraltypen
35
6.2.2
Aufnahme und Bearbeitung der Sternspektren
36
6.2.3
Auswertung der Sternspektren
36
6.2.4
Ergebnisse
37
Spektralanalyse von BD+33◦ 2642
45
◦
7.1
BD+33 2642
45
7.2
Bestimmung der fundamentalen Sternparameter
45
7.3
Elementhäufigkeiten
52
7.4
Vergleich mit der Arbeit von Napiwotzki et al.
52
Anhang 1
Das Midas-Skript ”phot.prg”
61
Anhang 2
Das Midas-Skript ”Spect.prg”
66
Literatur
68
1
Einleitung
In diesem Praktikum sollen die Grundlagen der praktischen Astronomie, Astrophysik und Spektroskopie
kennengelernt werden. Im einzelnen gliedert sich das Praktikum in drei Bereiche:
• Visuelle Beobachtungen, wie das Aufsuchen von Himmelsobjekten und der Bestimmung bestimmter Eigenschaften des Teleskopes wie die Bestimmung des Auflösungsvermögens und des Gesichtsfeldes.
• Die Aufnahme von Bildern mit der CCD-Kamera und die photometrische Auswertung eines offenen Sternhaufens.
• Die Aufnahme von Sternspektren und deren Analyse.
Kiel, den 11.11.2004
4
2
Visuelle Beobachtungen
Die visuelle Beobachtung ist der erste Teil des Praktikum und hat den Zweck, sich mit den Eigenschaften
und der Bedienung des Teleskopes vetraut zu machen.
2.1 Das Teleskop
Für die Beobachtungen stehen zwei Teleskope zur Verfügung. Zum einen ein 10”-Reflektor, welcher wahlweise
im Ritchey-Chrétien-Fokus (f=2000 mm) oder im Cassegrain-Fokus (f=3750 mm) betrieben werden kann.
Während der RC-Fokus für Deep-Sky-Objekte die geeignete Wahl ist, kann mit dem Cassegrain-Fokus wegen
seiner wesentlich grösseren Brennweite ein Abbildungsmaßstab von 0.5 Bogensekunden/Pixel auf dem CCDChip erreicht werden (Im Vergleich zum Abbildungsmaßstab von 0.9 Bogensekunden/Pixel im RC-Fokus),
was ihn für hochauflösende Aufnahmen von Planeten geeignet macht. Zum anderen ist an dem Reflektor
ein Refraktor montiert, welcher mit seiner Öffnung von 110 mm und 600 mm Brennweite als Leitfernrohr
Verwendung findet, da das Auffinden von Objekten aufgrund des grösseren Gesichtsfeldes einfacher ist, als
mit den Hauptrohr. Befestigt sind beide Teleskope auf einer sogenannten ”Deutschen Montierung” und
werden in Rektaszension automatisch nachgeführt.
2.2 Aufsuchen von Himmelsobjekten
Da das Auffinden von Objekte - insbesondere von kleinen und lichtschwachen - mitunter sehr langwierig und
anstrengend sein kann steht ein NGC-MAX zur Verfügung. Dabei handelt es sich um einen Kleinstcomputer
zum Auffinden von Objekte aus verschiedenen Katalogen. Um den NGC-MAX zu benutzen ist es zuerst
notwendig, einen bekannten Stern in das Gesichtsfeld des Teleskops zu bringen und dann mittels dem Befehl
ALIGN STAR den gewählten Stern als Referenzstern zu definieren. Ausgehend von diesem Referenzstern
kann der NGC-MAX die relative Position von anderen Objekte anzeigen, die dann mit dem Teleskop leicht
aufzufinden sind. Laut Anleitung des NGC-MAX sollte man stets einen Stern im Osten als Referenzstern
auswählen um Zweideutigkeiten in der Position zu vermeiden. Um ein Objekt auszuwählen und aufzusuchen
muss die Katalognummer (Die NGC-MAX Datenbank enthält alle Objekte des Messier-, des NGC- und des
IC-Kataloges sowie ein Verzeichnis heller Sterne) des Objektes in die Konsole eingeben werden. Mit dem
Befehl GUIDE wird die relative Position, also die Entfernung vom momentanen Ort in Deklination und
Rektaszension in Grad anzeigt.
2.3 Gesichtsfeldmessung
Unter dem Gesichtsfeld eines Teleskop versteht man den Bereich in Grad, den man beim Blick durch das
Okular überblicken kann. Da sich die Vergrösserung eines Teleskops und damit das Gesichtsfeld aus dem
Quotienten aus Brennweite des Objektives und der Brennweite des Okulars ergibt, hängt das Gesichtsfeld
natürlich auch vom verwendeten Okluar ab. Die Größe des Gesichtsfeld läßt sich aus der Durchlaufzeit eines
Sterns durch das Gesichtsfeld berechnen.
Im Laufe eines synodischen Tages dreht sich die Erde, relativ zur Sonne einmal um ihre Achse. Da sich die
Erde in dieser Zeit auch auf ihrer Umlaufbahn um die Sonne weiterbewegt ist der siderische Tag, d.h. die Zeit
5
6
Visuelle Beobachtungen
zwischen zwei Durchgängen eines Fixsterns im Ortsmeridian um 3 Minuten und 56 Sekunden kürzer als der
mittlere Sonnentag. Damit beträgt die Dauer eines Sternentages 23 Stunden 56 Minuten und 4 Sekunden.
Ein Punkt auf dem Himmelsäquator bewegt sich also mit einer Winkelgeschwindigkeit von
360◦
23h 56m 4s
00
00
= 15.04 s ≈ 15 s .
Aus der Zeit T (in Sekunden), welche ein äquatornaher Stern braucht, um das Gesichtsfeld eines optischen
Systems zentral zu durchqueren, kann über die Formel
®=T
15 0
60 s
(2.1)
direkt das wahre Gesichtsfeld ® in Bogenminuten bestimmt werden. Hat ein Stern die Deklination δ, so läßt
sich die gemessene Zeit T 0 über die Formel:
T = T 0 cos(δ)
(2.2)
in die Durchlaufzeit T , welche der Stern am Äquator benötigen würde um das Gesichtsfeld zu queren,
umrechnen.
2.3.1 Messungen
Für die Bestimmung der Durchlaufzeiten wird der Stern α Leo gewählt. Da α Leo eine Deklination von
11.97◦ besitzt, müssen die Durchlaufzeiten gemäß Gl. (2.2) korrigiert werden. Folgende optische Systeme
werden hierbei betrachtet:
(i) ein 1000 Ritchey-Chrétien-Teleskop (f /8) mit einem 42 mm Okular
(ii) ein 4.400 Refraktor (f /5.5) mit einem 15 mm Okular
Vor Beginn der Messung wird der Stern im Gesichtsfeldes zentriert und anschließend mit Hilfe der Feinbewegung in Rektaszension leicht außerhalb positioniert. Die Zeitdifferenz zwischen dem Auftauchen des Sterns
am östlichen und dem Verschwinden am westlichen Gesichtsfeldrand wird durch Ablesen der Sternzeituhr
aufgenommen. Dabei werden für jedes der verwendeten optischen Systeme zwei Meßdurchgänge durchgeführt
und die erhaltenen Werte anschließend gemittelt.
Instrument
Refraktor (f /6), 15
Okular
mm
Ritchey-Chrétien
42 mm Okular
Durchlaufzeiten (in s)
298 / 291
144 / 147
mittlere Durchlaufzeit T’ (in s)
295
146
Standardabweichung von T’ (in s)
4.9
2.1
mittlere Durchlaufzeit T am Himmelsäquator (in s)
289
143
Standardabweichung von T am
Himmelsäquator (in s)
4.8
2.1
wahres Gesichtsfeld ® (in 0 )
72
36
Standardabweichung von ® (in 0 )
1.2
0.5
Tabelle 2.1. Ergebnisse der Bestimmung des wahren Gesichtsfeldes
(f /8),
2.4 Bestimmung des Auflösungsvermögens
7
2.3.2 Ergebnisse und Fehlerabschätzungen
In Tabelle 2.1 sind die Ergebnisse der Messungen zusammengestellt. Im Mittel ergibt sich eine Streuung der
Meßwerte von 3 Sekunden. Dieses Ergebnis liegt im Rahmen des verwendeten Meßverfahrens: Der Beobachter
am Teleskop kann die Kontaktzeiten auf ca. 1 Sekunde genau bestimmen und der Zeitnehmer die Uhr auf
ca. 1 Sekunde genau ablesen. Die restliche Zeitdifferenz läßt sich durch die nicht ganz zentrale Passage des
Sterns durch das Gesichtsfeld erklären. Nach Umrechnung der Transitzeit auf den Himmelsäquator mit Gl.
(2.2) folgt mit Gl. (2.1) für das Ritchey-Chrétien-Teleskop mit 42 mm Okular ein Gesichtsfeld von 36 0 und
für den Refraktor mit 15 mm Okular eines von 720 .
2.4 Bestimmung des Auflösungsvermögens
2.4.1 Das Auflösungsvermögen eines Teleskops
Das Auflösungsvermögen eines Teleskops ist nach unten beschränkt. Dieses resultiert aus dem Wellencharakter des Lichtes: Treffen zwei Strahlenbündel auf die Öffnung des Teleskops, so werden sie gebeugt. Aufgrund
der Interferenz der gebeugten Lichtstrahlen bildet sich ein konzentrisches Muster von dunklen und hellen
Bereichen aus. Für eine kreisförmige Öffnung ergibt sich als minimaler Winkelabstand:
λ
φ = 1.22 D
Im sichtbaren Wellenlängenbereich (λ ≈ 550 nm) folgt damit für das theoretische Auflösungsvermögen:
φ=
13.8
D cm
Für das verwendete 1000 Ritchey-Chrétien-Teleskop mit D = 25 cm ergibt sich also ein theoretisches
Auflösungsvermögen von φ = 0.600 . Dieser Wert gilt natürlich nur für ein ideal gefertigtes und kollimiertes
optisches System. In der Praxis ergibt sich als weitere Beschränkung die turbulente Konvektionsbewegung
in der Erdatmosphäre. Diese begrenzt das wahre Auflösungsvermögen meist auf Werte um 100 .
2.4.2 Messungen
Für die Bestimmung des Auflösungsvermögens des Teleskops werden mehrere Doppelsterne mit unterschiedlichen Abständen der Komponenten nach folgenden Kriterien ausgewählt:
• Die Sterne sollen zum Zeitpunkt der Beobachtung möglichst hoch über dem Horizont stehen. Bei geringer
Horizonthöhe ist die Luftruhe schlechter, da der Sehstrahl durch die turbulente Erdatmosphäre sehr viel
länger ist, als bei einer Beobachtung in Zenitnähe.
• Die Komponenten des Doppelsterns sollen ungefähr die gleiche scheinbare Helligkeit besitzen, um zu
verhindern, daß eine Komponente von der anderen überstrahlt wird.
Die Beobachtungsliste ist in Tabelle 2.2 zusammengefaßt. Um sicherzustellen, daß bei engen Doppelsternen die einzelnen Komponenten auch wirklich getrennt werden können, wird der Positionswinkel der Sekundärkomponente geschätzt.
8
Visuelle Beobachtungen
2.4.3 Diskussion der Ergebnisse
Am Abend des 08.05.2004 wurden zwischen 22:15 Uhr MEZ und 23:20 Uhr MESZ die in Tabelle 2.2 stehenden
Doppelsterne mit dem 1000 Ritchey-Chrétien (f /8) bei Vergrößerungen zwischen 100× und 160× beobachtet.
Die Erfassung des Positionswinkels erwies sich als recht kompliziert, da Haupt- und Sekundärkomponente
der entsprechenden Doppelsternsysteme jeweils ungefähr gleich hell waren. So wurde beim Stern ξ U M a
der Positionswinkel um 180◦ falsch geschätzt, da die einzelnen Komponenten des Systems gleich hell sind.
Während die ersten zwei Sterne noch einfach zu trennen waren, berührten sich die Beugungsscheibchen der
Sterne ξ U M a und λ Oph bereits und bei ζ Boo überlagerten sich die Beugungsscheibchen. Der Stern λ Cas
konnte hingegen gar nicht mehr aufgelöst werden. Das Auflösungsvermögen lag in dieser Nacht also bei ca.
0.800 , wurde also durch die Luftunruhe in der Erdatmosphäre herabgesetzt.
Doppelstern
Abstand
(in 00 )
P West
(in ◦ )
P Wlit
(in ◦ )
Bemerkungen
σ Crb
7.1
220-240
236
deutlich getrennt, schwarzer Zwischenraum
γ Leo
4.4
80-100
125
immer noch deutlich getrennt
ξ UMa
1.8
60
273
die Beugungsscheibchen berühren
sich
λ Oph
1.5
0
30
die Beugungsscheibchen berühren
sich
ζ Boo
0.8
240
300
aufgelöst,
Beugungsscheibchen
überlagern sich.
λ Cas
0.6
-
191
nicht mehr auflösbar
Tabelle 2.2. Beobachtete Doppelsterne
3
Systemeigenschaften der CCD-Kamera ST-7
Bis zur Mitte der 70er Jahre des 20. Jahrhunderts wurden vorwiegend photographische Platten als Detektoren
in der Astronomie verwendet. Mit der Entwicklung leistungsfähiger Halbleiterdetektoren wurden diese durch
CCD-Kameras ersetzt. Aus diesem Grund werden in dem folgenden Kapitel einige Eigenschaften einer CCDKamera erarbeitet.
3.1 Das Funktionsprinzip einer CCD-Kamera
Ein CCD Detektor besteht aus einem n-p-dotiertem Siliziumplättchen. Auf diesem befindet sich eine zweidimensionale Anordnung von Elektroden. Diese sind das Analogon zu den Silberhalogenidkörnchen einer
herkömmlichen Photoemulsion. Die Elektroden sind die Bildelemente der CCD-Kamera. Im Vergleich zur
Photoemulsion sind diese jedoch gleichmäßig über den CCD-Chip verteilt und besitzen eine einheitliche
Größe. Im Fall der ST7-E ist jedes Pixel 9 × 9 µm groß. Die Funktionsweise eines CCD-Detektors basiert auf
dem inneren Photoeffekt: Proportional zum einfallenden Licht sammeln sich Elektronen in dem Potentialtopf
der jeweiligen Elektrode. Nach erfolgter Belichtung wird die Ladungsverteilung auf dem CCD-Chip durch
Änderung der Poteniale zeilenweise ausgelesen und an den Bildrand geschoben. Dies wird als ladungsgekoppeltes Ausleseverfahren bezeichnet, daher also die Bezeichnung CCD (Charged-Coupled Device). Über
einen Verstärker werden die einzelnen Zeilen in einen Computer eingelesen. Die ursprüngliche Ladungsverteilung auf dem CCD kann nun als Bild betrachtet werden. Zusammenfassend kann also gesagt werden, daß
CCD-Detektoren gegenüber photographischen Platten folgende Vorteile haben:
• Linearität
• höhere Dynamik
• eine höhere Quanteneffizienz
Die beiden erstgenannten Eigenschaften sollen im folgenden ”Trockenversuch” näher untersucht werden.
9
10
Systemeigenschaften der CCD-Kamera ST-7
3.2 Technische Daten der ST-7
In diesem Praktikum wird eine CCD-Kamera der Firma Santa Barbara Instrument Group (SBIG) (Modell
ST-7E) verwendet, deren technische Daten in Tabelle 3.1 zusammengestellt sind. Die ST-7E unterscheidet
sich von der herkömmlichen ST-7 durch ihre höhere Empfindlichkeit im blauen Spektralbereich.
Imaging CCD
Tracking CCD
Chip
Kodak KAF 0401E
TI TC 211
Pixelzahl
765 × 510
192 × 164
Pixelgröße
9 µm x 9 µm
13.75 µm x 16 µm
Chipgröße
6.9 mm × 4.6 mm
2.6 mm × 2.6 mm
Bildfeld (Ritchey-Chrétien)
11.2
arcmin
7.6 arcmin
Abbildungsmaßstab
0.9 arcsec/P ixel
Full Well Capacity
×
4.3
arcmin
4.3 arcmin
×
1.4
1.6 arcsec/P ixel
×
100000
A/D Converter
16 bit
Gain
2.3 e− /ADU
Ausleserauschen
15 e− (RM S)
Tabelle 3.1. Technische Daten der CCD-Kamera ST-7E (Daten aus der Praktikumsanleitung entnommen).
3.3 Durchführung des ”Trockenversuchs”
3.3.1 Ausleserauschen (”Readout noise”)
Zur Bestimmung des Ausleserauschens wird ein Dunkelbild ohne Licht mit einer Belichtungszeit von 1 Minute
aufgenommen (Abbildung 3.1). Mit der Histogrammfunktion von CCDOPS wird eine mittlere Intensität der
Pixel von 70 bestimmt (RM S = 7.36). Deutlich erkennbar ist ein ”hot strip” - eine weiße Linie, welche das
Dunkelbild durchzieht. Mit der Cursorfunktion von CCDOPS werden für diese Streifen Intensitäten von 65
bis 95 bestimmt. Für das Rauschen ergeben sich Werte von 3 − 5.
3.3.2 Dunkelstrom (”Dark current”)
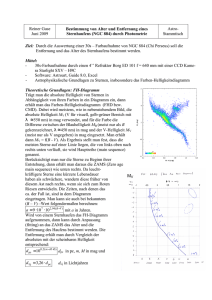
Für die Bestimmung der Temperaturabhängigkeit des Dunkelstromes werden Dunkelbilder mit einer Belichtungszeit von einer Minute für Temperaturen von 0◦ C bis 25◦ C erstellt: In Abbildung 3.2 ist die mittlere
Intensität I der einzelnen Dunkelbilder über der Temperatur T aufgetragen. Es ist ein nichtlinearer Verlauf
der Intensität als Funktion der Temperatur erkennbar. Weiterhin fällt auf, daß die Fehlerbalken (das ”Rauschen”) mit zunehmender Temperatur größer werden. Dieses kann dadurch erklärt werden, daß das Auslösen
von Elektronen aus dem Halbleiter, bedingt durch die thermische Bewegung, mit steigender Temperatur immer größer wird - ein Nachteil von CCD-Kameras, welcher jedoch durch Kühlung des CCD-Chips reduziert
werden kann.
3.3 Durchführung des ”Trockenversuchs”
11
Abb. 3.1. Dunkelbild mit einer Belichtungszeit von 1 Minute.
Temperaturabhängigkeit des Dunkelstroms
700
600
Mittlere Intensität
500
400
300
200
100
0
−100
0
5
10
15
20
T [°C]
Abb. 3.2. Nichtlineare Temperaturabhängigkeit des Dunkelstroms bei einer Belichtungszeit von 60 Sekunden.
data 1
shape−preserving
data 2
data 3
12
Systemeigenschaften der CCD-Kamera ST-7
Temperatur (◦ C)
Mittelwert
RM S
0.23
70
88.87
4.89
77
127
9.78
90
177
14.96
126
244
20.05
186
319
24.46
304
423
Tabelle 3.2. Ergebnisse der Dunkelstrommessungen
3.3.3 Linearität
Bei der Aufnahme von Pseudo-Flatfields mit einer Belichtungszeit t von 0.11 s bis 240 s ergeben sich die in
Tabelle 3.3 zusammengefaßten Werte. In der graphischen Darstellung der Meßwerte (Abbildung 3.3) werden
die RMS-Werte als Fehlerbalken geplottet.
Dynamikbereich der CCD−Kamera
4
x 10
6
Mittlere Intensität
5
4
3
2
1
0
50
100
150
Belichtungszeit [s]
200
Abb. 3.3. Der Dynamikbereich der CCD-Kamera
Mit MATLAB 6.5 wird an die ersten 18 Meßwerte eine lineare Funktion gefittet:
I(t) = 11.55t + 321.19
Es zeigt sich, daß die Meßwerte kaum um diese Funktion streuen.
3.3 Durchführung des ”Trockenversuchs”
Belichtungszeit (s)
Mittlere Intensität
RMS
0.11
81
6.75
0.5
190
10.7
1
339
15.31
1.5
492
19.50
3
957
32.47
5
1568
1696
8
2545
74.29
12
3838
108
15
4809
5121
18
5782
158
20
6424
174
22
7079
192
23
7403
200
24
7728
208
25
8054
216
26
8376
244
27
8641
232
30
9667
257
120
35097
381
180
45253
382
210
47345
565
240
50786
1264
13
Tabelle 3.3. Ergebnisse der Linearitätsmessungen
Diese Vermutung bestätigt der Wert des Korrelationskoeffizient r = 0.99854, welcher mit Hilfe von MATLAB
bestimmt wurde. Damit folgt, daß in dem Zeitbereich zwischen 0.11 und 50 Sekunden ein linearer Zusammenhang zwischen der Belichtungszeit und der mittleren Intensität besteht. Oberhalb dieses Zeitbereichs ist
die Abhängigkeit zwischen Belichtungszeit und mittlerer Intensität nichtlinear.
Abb. 3.4. Flat-Field-Aufnahme durch ein Clear-Filter.
4
Aufnahmen mit der CCD-Kamera
In diesem Abschnitt sind die Aufnahmen unterschiedlicher Himmelsobjekte zusammengestellt. Weiterhin werden die einzelnen Schritte von der Aufnahme über die Verarbeitung bis zum endgültigen Resultat ausführlich
erläutert.
4.1 Schwarz-Weiß-Aufnahmen
4.1.1 Bearbeitung der Schwarz-Weiß-Aufnahmen
Die Bearbeitung der Aufnahmen erfolgt mit Hilfe des Programms CCDOPS. In Abbildung 4.2 ist die
Prozessing-Sequenz einer Schwarz-Weiß-Aufnahme am Beispiel des Crabnebels, aufgenommen mit einer Belichtungszeit von 240 s durch ein Clear-Filter dargestellt. Nach der Aufnahme des Himmelsobjektes mit der
CCD-Kamera (siehe Abbildung 4.2, Oben), muß ein gleichlang belichtetes Dark-Frame abgezogen werden,
um das thermische Rauschen des CCD-Chips, sowie das Ausleserauschen des Verstärkers zu unterdrücken.
Das Ergebnis zeigt Abbildung 4.2 (Mitte). Im letzten Bearbeitungsschritt wird eine Flatfield-Aufnahme abgezogen, um einen gleichmäßigen Himmelshintergrund des Endresultates zu gewährleisten (Abbildung 4.2,
Unten). In den folgenden Abschnitten sind einige Aufnahmen verschiedener Himmelsobjekte zusammengestellt.
4.1.2 Die Galaxie M 51 (Whirlpool-Galaxy)
Belichtungszeit: 1x240 Sekunden im Clear-Filter. M 51 ist das dominierende Mitglied einer kleinen Gruppe
von Galaxien und war die erste Galaxie bei der die Spiralstruktur entdeckt wurde (Lord Rosse, 1845). M 51
verfügt über eine Begleitergalaxie mit der sie wechselwirkt.
Abb. 4.1. Aufnahme der Whirlpool-Galaxie M 51.
14
4.1 Schwarz-Weiß-Aufnahmen
15
Abb. 4.2. Prozessing-Sequenz einer Schwarz-Weiß-Aufnahme.Originalaufnahme (oben), Aufnahme nach Abzug des
Dark-Frames (Mitte) und Aufnahme nach Flat-Field Korrektur (unten).
16
Aufnahmen mit der CCD-Kamera
4.1.3 Die Galaxie NGC 891
Belichtungszeit: Komposit aus zwei Aufnahmen (1x240 Sekunden und 1x360 Sekunden) im Clear-Filter.
Die Galaxie NGC 891 befindet sich zwischen den Sternbildern Andromeda und Perseus (RA = 2h 23m,
DE = +42.3◦ ). Am Himmel besitzt sie eine scheinbare Ausdehnung von 130 × 2.80 , sowie eine scheinbare
Helligkeit von 10 mag. Von der Erde aus sehen wir auf die Kante dieser Galaxie, so daß die in den Spiralarmen verteilten Staubmassen deutlich als schwarzes Band vor dem Galaxienkern zu sehen sind. Auf der
Detailaufnahme (Abbildung 4.3, unten) sind zwei Galaxien im Hintergrund gekennzeichnet. Das es sich bei
diesen Objekten nicht etwa um Sternhaufen handelt die Galaxien üblicherweise begleiten, zeigt folgende
Quelle: http://www.astrode.de/ngc891.htm
Abb. 4.3. Aufnahme der Edge-On Galaxie NGC 891 im Perseus (oben), Detailvergößerung mit zwei Hintergrundgalaxien (unten).
4.1.4 Die Galaxie M 101 (Pinwheel-Galaxy)
Belichtungszeit: 1x240 Sekunden im Clear-Filter.
M 101 ist die hellste einer Gruppe von mindestens neun Galaxien; die hellsten Begleiter sind NGC 5474 und
NGC 5585. Die anderen Mitglieder der Gruppe sind: NGC 5204, NGC 5238, NGC 5477, UGC 8508, UGC
8837, und UGC 9405. Die Entfernung von M 101 wurde 1994/95 durch das Hubble Space Telescope durch
4.1 Schwarz-Weiß-Aufnahmen
17
die Vermessung von Cepheiden zu 24 Millionen Lichtjahren bestimmt. Unsere Fotographie ist eher dürftig,
ein Composite aus vielleicht 10x60 Sekunden würde die Spiralarme gewiss besser hervorbringen.
Abb. 4.4. Aufnahme der Galaxie M 101.
4.1.5 Der offene Sternhaufen NGC 654 in der Cassiopeia
Belichtungszeit: 5 Minuten im grünen, 8 Minuten im blauen Filter.
NGC 654 hat eine Entfernung von rund 7000 Lichtjahren und eine Ausdehnung von rund fünf Bogenminuten.
Die mittlere scheinbare Helligkeit beträgt 10 mag.
Abb. 4.5. Aufnahme des offenen Sternhaufens NGC 654.
18
Aufnahmen mit der CCD-Kamera
4.1.6 Der Kugelsternhaufen M 3
Mit ungefähr einer halben Million Sternen ist M 3 einer der herausragendsten Kugelsternhaufen. Er besitzt
eine extrem große Zahl von variablen Sternen: Laut B. Madore (in Hanes/Madore, Globular Clusters, 1978),
sind 212 variable Sterne entdeckt worden, wobei man von 186 die Perioden bestimmen konnte.Man hat
mindestens 170 RR Lyrae Veränderliche entdeckt.
Abb. 4.6. Aufnahme des Kugelsternhaufens M 3.
4.1.7 Der offene Sternhaufen M 52
Belichtungszeit: 240 Sekunden im Clear-Filter.
Die Entfernung von M 52 ist unklar, der Sky Catalog 2000 gibt einen Wert von 5200 Lichtjahren an. Andere
Autoren sprechen hingegen von lediglich 3000 Lichtjahren. Ake Wallenquist fand im Jahr 1959 193 mögliche
Haufenmitglieder in einer Region von 9 Bogenminuten Radius.
Abb. 4.7. Aufnahme des offenen Sternhaufens M 52.
4.1 Schwarz-Weiß-Aufnahmen
19
4.1.8 Der Komet C/2003 K4 (Linear)
Am 28.Mai 2003 entdeckte das LINEAR-Team im Grenzbereich Schwan/Füchschen einen 17.5 mag hellen
Kometen mit einer 6” kleinen, gering kondensierten Koma. Wenige Tage später konnte eine vorläufige Bahn
ermittelt werden, nach der der Komet bis Anfang September bei einer Helligkeit von ca. 6.5 m bequem von
Mitteleuropa beobachtbar sein sollte (IAUC 8139/45). Am 14.8.2004 konnten wir den Kometen gegen 23:38
MESZ in einer Höhe von ca. 10◦ über dem Westhorizont ausmachen. Trotz der schlechten Seeingbedingungen in Horizontnähe, ließ sich die innere Koma des Kometen bei einer Belichtungszeit von 3x240 s deutlich
abbilden (Abbildung 4.8). Man beachte die starke Eigenbewegung des Kometen während des Aufnahmezeitpunkts, deutlich erkennbar an den Strichspuren der Sterne. Um den auf der Aufnahme nicht sichtbaren Kern
des Kometen ist die Staub-/Gaskonzentration besonders hoch, so daß die Koma dort heller erscheint (false
nucleus). Zudem fällt die leicht asymmetrische Staub/Gasverteilung in Richtung des Kometenschweifs auf,
was auf unregelmäßig verteilte Aktivitätsgebiete auf der Oberfläche des Kometenkerns schließen läßt.
Abb. 4.8. Aufnahme der inneren Koma des Kometen C/2003 K4 (Linear).
20
Aufnahmen mit der CCD-Kamera
4.2 Farbaufnahmen
Werden 3 Aufnahmen durch einen Rot-, einen Grün- und einen Blaufilter gewonnen, so lässt sich aus diesen
ein RGB-Komposit erstellen.
4.2.1 Bearbeitung der Farbaufnahmen
Analog zur Bearbeitung der Schwarz-Weiß-Aufnahmen muß bei jedem Farbkanal eine Dark-Frame und FlatField-Korrektur angebracht werden. Die einzelnen Aufnahmen der unterschiedlichen Farbkanäle lassen sich
anschließend unter CCDOPS mit der Funktion ”RGB-Composit” zu einem RGB-Komposit zusammenstellen. Dies zeigt beispielhaft die Abbildung 4.10, drei Aufnahmen des planetarischen Nebels M 27 mit einer
Belichtungszeit von 240 s durch jeweils einen Rot-, Grün- und Blau-Filter. In der Rot-Aufnahme dominiert
das rote ”Hα-Leuchten”, in der Grün- und Blau-Aufnahme das ”O III-Leuchten” des zweifach ionisierten
Sauerstoffs. Einige weitere Farbaufnahmen finden sich in den folgenden Abschnitten.
4.2.2 Der Crabnebel M 1
Belichtungszeit: 300 s pro Farbkanal. Der Crabnebel M 1 ist der Überrest einer Supernova, welche im Jahr
1054 nach Christus explodierte. Am Himmel besitzt M 1 eine scheinbare Ausdehnung von 6’x 4’ und eine
scheinbare Helligkeit von 8.4 mag. Im Zentrum des Nebels befindet sich ein Pulsar mit einer scheinbaren
Helligkeit von ca. 16 mag (in Abbildung 4.9, unten mit einem Pfeil markiert.)
Crab−Pulsar
Abb. 4.9. RGB-Komposit des Crab-Nebels (oben), sowie eine Detailvergrößerung der Aufnahme (unten). Die Position
des Pulsars ist durch einen Pfeil markiert.
4.2 Farbaufnahmen
21
Abb. 4.10. Prozessing-Sequenz einer Farb-Aufnahme: Aufnahmen von M 27 durch einen Rot- (oben links), einen
Grün- (oben rechts) und einen Blau-Filter (Mitte). Nach der Anwendung der CCDOPS-Funktion ”RGB-Composit”
ergibt sich die unten dargestellt Farbaufnahme.
22
Aufnahmen mit der CCD-Kamera
4.2.3 Der Ringnebel M 57
Belichtungszeit: Jeweils 240 Sekunden im roten, grünen und blauen Filter.
M 57 ist der Prototyp unter den Planetarische Nebeln. Das Gas wurde einst von dem Zentralstern abgestossen
der es jetzt ionisiert. Seine Entfernung beträgt 4100 Lichtjahre.
Abb. 4.11. RGB-Komposit des Ringnebels M 27 in der Leier.
4.2.4 Der planetarische Nebel M 27 im Füchslein
Der Dumbbell Nebel M 27 war der erste planetarische Nebel, der überhaupt entdeckt worden ist. Am 12. Juli
1764 entdeckte Charles Messier diese Klasse von Objekten. Man spricht von planetarischen Nebel, da sie in
kleinen Teleskopen wie Planeten aussehen. Wir sehen dieses Objekt fast genau von seiner Äquatorialebene.
Würde man ihn von einem der Pole sehen, würde er wahrscheinlich die Form eines Ringes aufweisen und in
seinem Aussehen M 57 ähneln.
Abb. 4.12. Der Plantarische Nebel M 27.
4.2 Farbaufnahmen
23
4.2.5 Der Planetarische Nebel NGC 6781
Belichtungszeit: Jeweils 240 Sekunden im roten, grünen und blauen Filter. Bei NGC 6781 handelt es sich
wie bei M 27 und M 57 um einen planetarischen Nebel.
Abb. 4.13. Der Plantarische Nebel NGC 6781.
24
Aufnahmen mit der CCD-Kamera
4.3 Hochauflösende Mond- und Planetenaufnahmen
Im folgenden Abschnitt werden einige Objekte unseres Sonnensystems betrachtet. Auf eine detaillierte Darstellung muß aus Platzgründen leider verzichtet werden. Es wird daher auf Beatty, Petersen, Chaikin, ”The
New Solar System” verwiesen.
4.3.1 Saturn
4.3.1.1 Aufnahme und Bildbearbeitung
Die Aufnahmen von Saturn entstanden am 04.09.2004 um 05:18 Uhr MESZ. Aufgrund seiner günstigen
Position im Sternbild Zwillinge und dem guten Seeing waren brauchbare Ergebnisse zu erwarten. Es wurde
also eine Serie von 15 Aufnahmen pro Filter (RGB) zu jeweils 0.11 Sekunden im Ritchey-Chrétien-Fokus des
Teleskops belichtet. Die weitere Verarbeitung der Aufnahmen erfolgt mit dem Programm CCDOPS: Zunächst
wird jede der Einzelaufnahmen mit der Option ”Sharpen” (lunar-planetary, hard) zweimal geschärft. Das
Ergebnis wird um den Faktor zwei vergrößert (enlarge image 2×). Nach diesen beiden Bearbeitungsschritten
ergibt sich ein stark verrauschtes Bild. Um das Rauschen etwas zu unterdrücken, werden die Einzelaufnahmen
mit dem Befehl ”Crop” ausgeschnitten und anschließend mit ”Co-Add” aufaddiert. Das Resultat ist in
Abbildung 4.14 (oben, rechts) dargestellt. Zum Vergleich findet sich in Abbildung 4.14 (oben, links) ein RGBKomposit aus einer einzelnen Rohaufnahme. Auf diesem sind so gut wie gar keine Details erkennbar. Das mit
der oben beschriebenen Prozessing-Sequenz erzielte Resultat zeigt ansatzweise die Cassini-Teilung im Ring,
sowie ein rostrotes Wolkenband in der Saturnatmosphäre. Die ”Polkappe” des Planeten erscheint hellbraun.
Das Saturnscheibchen ist noch relativ klein. Bessere Ergebnisse lassen sich während der Opposition erzielen.
Eine 30 Sekunden lang belichtete Aufnahme zeigt deutlich die Saturnmonde Titan, Rhea und Enceladus
(Abbildung 4.14, unten).
Enceladus
Titan
Rhea
Abb. 4.14. RGB-Komposit des Planeten Saturn vor Anwendung der Prozessing-Sequenz (oben links), nach Anwendung der Prozessing-Sequenz (oben rechts). Die größten Monde des Saturn (unten).
4.3 Hochauflösende Mond- und Planetenaufnahmen
25
4.3.2 Mond
Der Mond umkreist die Erde in einer mittleren Entfernung von 384000 km. Aufgrund seiner Nähe lassen
sich auf seiner Oberfläche selbst mit einem kleinen Teleskop eine Vielfalt von unterschiedlichen geologischen
Strukturen ausmachen: Vulkane, Lavaströme, Gebirge und Meteoritenkrater.
4.3.2.1 Mondbeobachtungen
Bei außergewöhnlich guten Seeingbedingungen konnten am Morgen des 4.9.2004 um 5:29 Uhr MESZ sehr
hochauflösende Mondaufnahmen gewonnen werden. Die Belichtungszeit durch einen Blaufilter lag bei 0.11
s. Außer einer leichten Schärfung der Aufnahme mit CCDOPS (lunar-planetary, hard), wurde keine Bildbearbeitung durchgeführt.
4.3.2.2 Meteoritenkrater, Rillen und Vulkane
Das erste was einem bei einer Untersuchung der Mondaufnahmen auffällt ist die große Anzahl von Kratern.
Diese sind meist durch Einschläge von mehr oder weniger großen Meteoriten entstanden. Die Größe des
einschlagenden Körpers bestimmt das spätere Erscheinungsbild der Meteoritenkrater. Meteoriten mit einem
Durchmesser von unter einem Kilometer erzeugen einfache schüsselförmige Krater mit einem Durchmesser
von bis zu 25 km. Oberhalb dieser Grenze werden die Krater komplexer, d.h. sie besitzen z.B. eine zentrale
Aufwölbung oder einen terrassierten Kraterrand. Abbildung 4.15 zeigt eine Gruppe von drei großen Kratern. Von Norden nach Süden sind dies Theophilus, Cyrillus und Catharina. An dieser Dreiergruppe kann
das relative Alter von Strukturen auf der Mondoberfläche bestimmt werden. Als erstes entstand Cyrillus,
ihm überlagert ist Catharina; am jüngsten ist Theophilus, welcher im Nordostrand von Cyrillus entstand.
Auffällig ist auch, daß der junge Krater Theophilus scharfe Kraterränder besitzt, während die älteren Krater
deutlich erodierte Ränder besitzen. Nördlich des ”Krater-Trios” liegt das Mare Tranquillitatis. Im Vergleich
mit der Umgebung ist die Kraterdichte in dem mit dunkler Lava gefüllten Einschlagbecken sehr viel geringer.
Daraus folgt, daß die Oberfläche aufgrund des Vulkanismus in dieser Region jünger ist. Spuren des Vulkanismus im Mare Tranquillitatis sind in Abbildung 4.16 dargestellt. Nahe am Terminator finden sich mehrere
rundliche Strukturen, bei denen es sich um vulkanische Dome handelt. Diese Aufwölbungen der Mondoberfläche entstanden durch Ansammlungen von Magma unter der Mondoberfläche. Einige dieser Dome besitzen
kleine Krater an der Oberfläche, aus denen bis vor 3 Mrd. Jahren noch Asche und Gase gefördert wurden.
Man könnte diese Strukturen also auch als ”Mondvulkane” bezeichnen. Weitere Spuren von Vulkanismus
sind in Abbildung 4.17 dargestellt. Südlich des Mare Serenitatis wird das Mondhochland von zwei Rillen,
der Ariadaeus und der Hyginus-Rille durchschnitten. Diese entstanden durch den Einsturz von leeren Lavakanälen. Ein intakter Lavakanal befindet sich nahe des Ostrandes des Mare Serenitatis Auf den Aufnahmen
lassen sich noch unzählige weitere Details erkennen. Hier konnten aus Platzgründen nur die wichtigsten
zusammengefaßt werden. Für weitergehende Informationen sei auf J.Lacroux, Chr. Legrand: ”Der Kosmos
Mondführer” verwiesen.
26
Aufnahmen mit der CCD-Kamera
Mare Tranquilitatis
Theophilus
Cyrillus
Catharina
Abb. 4.15. Die Mondkrater Theophilus, Cyrillus und Catharina.
Dome
Abb. 4.16. Vulkanische Dome am Ostrand des Mare Tranquilitatis.
27
Mare Tranquilitatis
Ariadaeus−Rille
Hyginus−Rille
Lavastrom
Mare Serenitatis
Posidonius
4.3 Hochauflösende Mond- und Planetenaufnahmen
Abb. 4.17. Mond-Rillen und Lavaströme im Bereich der Maria Serenitatis und Tranquilitatis.
5
Photometrische Aufgaben
5.1 Photometrie von DY-Peg
DY Pegasi (DY Peg) ist ein Veränderlicher vom Typ δ Sct, dessen Lichtwechsel auf einer Pulsation des
Sterns beruhen. Insofern sind sie den δ Cepheiden verwandt, deren Periode mit ihrer Absoluten Helligkeit
verknüpft ist, so daß sie sich als ”Standardkerzen” zur Entfernungsbestimmung eignen. δ Sct Sterne zeichnen
sich insbesondere durch eine kurze Periode (max. 0.2 d, d.h. ca. 5 Stunden) aus, so daß man bei einigen dieser
Sterne schon innerhalb einer Beobachtungsnacht eine komplette Periode beobachten kann. DY Peg wurde
auf Grund seiner besonders kurzen Periode von 0.0726297 d oder ca 1 h 44 min (TheSky) ausgewählt. Für
die Änderung der Helligkeit findet man in der Literatur 0.67 mag. Abbildung 5.1 zeigt das Sternenfeld, in
dem sich DY Peg befindet. Neben dem zur Photometrie benötigten Vergleichsstern sind auch einige anonyme
Galaxien in der unmittlbaren Nachbarschaft des Veränderlichen eingezeichnet.
5.1.1 Aufnahme und Bearbeitung
Am Morgen des 15.8.2004 wurde zwischen 03:30 Uhr und 04:50 Uhr MESZ mit der CCDOPS-Funktion
AUTO-GRAB eine Serie von Aufnahmen mit einer Belichtungszeit von jeweils 1 Minute aufgenommen.
Nach der Darkframe- und Flatfield-Korrektur konnten der Veränderliche und der Vergleichsstern mit Hilfe
von CCDOPS photometrisch vermessen werden. Datum, Uhrzeit und Helligkeiten von DY Peg und dem
Vergleichsstern wurden anschließend mit MATLAB geplottet (Abbildung 5.2).
5.1.2 Interpretation der Ergebnisse
Während der Vergleichsstern eine konstante Helligkeit aufweist, zeigt DY Peg eine deutliche Zunahme der
Helligkeit. Ab 3:40 Uhr MESZ scheinen plötzlich beide Sterne schwächer zu werden. Dies ist auf die einsetzende Dämmerung zurückzuführen. Plottet man die Differenz zwischen den Helligkeiten von DY Peg und dem
Vergleichsstern, so ist die Lichtkurve mit einem ausgeprägten Maximum deutlich erkennbar (Abbildung 5.3).
Das Maximum läßt sich graphisch zu 03:53 Uhr MESZ bestimmen. Der Abstieg zum folgenden Minimum
ließ sich aufgrund der einsetzenden Dämmerung nicht mehr verfolgen. Der Helligkeitsanstieg, bzw. Abfall
beträgt ca. 0.4 mag.
28
29
Vergleichsstern
DY Peg
5.1 Photometrie von DY-Peg
Abb. 5.1. Das Sternenfeld um DY Peg mit dem verwendeten Vergleichsstern, sowie einigen anonymen Galaxien.
30
Photometrische Aufgaben
Lichtkurven von DY Peg und dem Vergleichsstern
14.5
14
Scheinbare Helligkeit [m]
13.5
13
12.5
12
11.5
11
10.5
10
03:30
03:45
04:00
04:15
04:30
Uhrzeit MESZ [h:m] 15.August 2004
04:45
05:00
Abb. 5.2. Lichtkurven von DY-Peg und dem Vergleichsstern. Man beachte das ”Verblassen” der Sterne mit einsetzender Dämmerung.
Differenzlichtkurve zwischen DY Peg und dem Vergleichsstern
3.05
3
Scheinbare Helligkeit [m]
2.95
2.9
2.85
2.8
2.75
2.7
2.65
2.6
2.55
03:30
03:45
04:00
04:15
04:30
Uhrzeit MESZ [h:m] 15.August 2004
04:45
Abb. 5.3. Differenzlichtkurve von DY-Peg und dem Vergleichsstern.
05:00
5.2 Farben-Helligkeitsdiagramm von NGC 654
31
5.2 Farben-Helligkeitsdiagramm von NGC 654
Das Hertzsprung-Russell-Diagramm ist das wichtigste Zustandsdiagramm der Astrophysik. Es stellt auf
sehr kompakte Weise die wesentlichen Parameter von Sternen, sowie deren Entwicklung dar. Im folgenden
Abschnitt wird eine Variante dieses Diagrammes näher erläutert, das Farben-Helligkeits-Diagramm.
5.2.1 Das Farben-Helligkeits-Diagramm
In einem Hertzsprung-Russell-Diagramm ist die absolute Helligkeit (Leuchtkraft) über dem Spektraltyp
(Temperatur) verschiedener Sterne, z.B. eines Sternhaufens aufgetragen. Da der Spektraltyp bei schwachen Sternen schwer zu bestimmen ist, kann es von Vorteil sein, statt des Spektraltyps den Farbindex zu
verwenden. Dieser läßt sich aus photometrischen Beobachtungen in zwei eng begrenzten Spektralbereichen
gewinnen. Um die Ergebnisse mit anderen Beobachtungen einfacher vergleichen zu können, muß ein ”Standardfarbsystem” festgelegt werden. Am gebräuchlichsten ist das Johnson UBVRI-System. Die Differenz der
Helligkeiten in zwei dieser Spektralbereiche wird dann als Farbindex bezeichnet. In dem weiter unten dargestellten Farben-Helligkeits-Diagramm wird die scheinbare Helligkeit über der Helligkeitsdifferenz in einem
Blau (B)- und einem Grün (V )-Filter, also dem Farbindex B − V aufgetragen. Da ein Sternhaufen untersucht wird, ist es unwichtig, ob die absolute, oder die scheinbare Helligkeit verwendet wird, da die Sterne
in dem Haufen ungefähr alle die gleiche Entfernung zur Erde besitzen. Dies führt nur zu einem konstanten
Summanden bei der Bestimmung der absoluten Helligkeit MV :
MV = 5 − 5 log r + mV = const. + mV ,
wobei r die Entfernung des Sternhaufens in pc ist.
5.2.2 Der offene Sternhaufen NGC 654
◦
Der offene Sternhaufen NGC 654 befindet sich in der Cassiopeia bei RA = 01h 44m und DE = 61 530 . Er
besitzt eine scheinbare Helligkeit von 6.5 mag und einen Durchmesser von 5 0 . Insgesamt gehören 60 Sterne zu
diesem offenen Sternhaufen, der hellste besitzt eine Helligkeit von 7.4 mag, 50 Sterne besitzen eine Helligkeit
von 11 bis 14 mag. (Quelle: http://dvaa.org/servlets/Sac?item=NGC654).
5.2.3 Aufnahme und Bildverarbeitung von NGC 654
Für die Erstellung eines Farben-Helligkeits-Diagramms werden zwei Aufnahmen benötigt, die mit unterschiedlichen Filtern aufgenommen wurden. Aus diesen lassen sich dann mit Hilfe eines geeichten Standardsterns die Helligkeiten der Sterne in den unterschiedlichen Spektralbereichen bestimmen. Aus diesen kann
der Farbindex B −V bestimmt werden. In der Nacht vom 14. auf den 15. August 2004 wurden zwischen 01:35
Uhr MESZ und 2:53 Uhr MESZ unter guten Seeingbedinungen (R = 3, D = 2) die B und V -Aufnahmen im
Ritchey-Chrétien-Fokus gewonnen. Für die V -Aufnahme wurde ein Grünfilter verwendet. Die Belichtungszeit
betrug 5 Minuten. Durch den Blaufilter wurde 10 Minuten belichtet. Außer dem Abzug eines Dunkelbildes
und der Addition der einzelnen Blauaufnahmen mit dem Programm CCDOPS (”CO-ADD”) wurden die
Aufnahmen nicht bearbeitet. Das Ergebnis ist in Abbildung 5.4 dargestellt.
5.2.4 Erstellung des Farben-Helligkeits-Diagramms
Für die Auswertung der Aufnahmen werden diese in das FITS-Format konvertiert. Die Auswertung erfolgt mit dem Midas-Skript ”phot.prg”. Dieses führt neben der Photometrie der einzelnen Sterne auch eine
Flatfield-Korrektur durch. Der Eichstern besitzt im V-Filter eine Helligkeit von 11.48 mag sowie eine Fabindex B − V von 0.69 mag. Nach Auswahl der einzelnen Sterne auf der Aufnahme werden diese von dem
Programm ”phot.prg” automatisch photometriert. Mit Hilfe des Eichsterns werden die scheinbaren Helligkeiten der Sterne in Magnitudines umgerechnet. Eingetragen in ein (B − V ) − V -Diagramm ergibt sich
Abbildung 5.5.
32
Photometrische Aufgaben
5.2.5 Interpretation des Farben-Helligkeits-Diagramms
Ist ein Stern im B-Filter schwächer als im V -Filter, der B − V -Wert also positiv, so ist der Stern rötlich. Im
umgekehrten Fall ist der Stern bläulich (B − V -Wert ist klein oder negativ). Die blauen Sterne befinden sich
im Farben-Helligkeits-Diagramm also links, die Roten weiter rechts. Das Farben-Helligkeits-Diagramm von
NGC 654 wird diagonal von einer Hauptreihe durchzogen, wobei die Messwerte jedoch sehr stark streuen.
Zur weiteren Interpretation des FHD nutzen wir aus, daß die scheinbare V-Helligkeit ein direktes Maß für
die Leuchtkraft eines Sterns ist. Für die Sterne auf der Hauptreihe gilt die Masse-Leuchtkraftbeziehung:
log L = 3.8 log M + 0.08
Aus dieser empirischen Beziehung wird entnommen, daß im unteren Bereich der Hauptreihe die massearmen
Sterne und im oberen Bereich der Hauptreihe (bei kleinen scheinbaren Helligkeiten) die massenreichen Sterne
liegen.
Abb. 5.4. V -Aufnahme des offenen Sternhaufens NGC 654.
5.2 Farben-Helligkeitsdiagramm von NGC 654
Abb. 5.5. Farben-Helligkeits-Diagramm des offenen Sternhaufens NGC 654.
33
6
Aufnahme von Sternspektren
Die Spektroskopie gehört zu den Verfahren in der Astrophysik, welche Informationen über die Zustände und
Dynamik der Objekte im Weltraum liefern. Anhand von einigen Beispielen werden im folgenden Abschnitt
die unterschiedlichen Anwendungsmöglichkeiten der Spektroskopie dargestellt.
6.1 Der Spektrograph
Im Praktikum wird der SBIG Self Guided Spectrograph verwendet. Bei diesem handelt es sich um einen
Gitterspektrographen. Dieser besitzt gegenüber einem Prismenspektrographen den Vorteil einer linearen Dispersion, was die Auswertung der Sternspektren erleichtert. Der Spektrograph kann mit vier unterschiedlichen Auflösungen betrieben werden. Dies läßt sich durch Änderung der Spaltbreite oder durch Austausch des
Blaze-Gitters erreichen (Tabelle 6.1). Der Wellenlängenbereich beträgt in der niedrigen Dispersion 320 nm,
in der höheren 75 nm.
Spalt
Gitter (Linien pro mm)
∆λ (in nm)
breit
150
3.8
breit
600
1.0
schmal
150
1.0
schmal
600
0.24
Tabelle 6.1. Kenndaten des SBIG Self Guided Spectrograph (der Praktikumsanleitung entnommen).
34
6.2 Sequenz der Spektraltypen von O bis M
35
6.2 Sequenz der Spektraltypen von O bis M
Aus dem Spektrum eines Sterns lassen sich Rückschlüsse auf den Zustand seiner Atmosphäre ziehen. Dieses
soll anhand von mehreren Sternen des Sommerhimmels demonstriert werden.
6.2.1 Die Spektraltypen
Die Klassifikation von Sternspektren erfolgt über den Spektraltyp. Dieser beschreibt die in dem Spektrum
auftretenden Linien und ist damit ein Maß für die Temperatur der Atmosphäre eines Sterns. Die Verknüpfung
zwischen Temperatur und Stärke der auftretenden Spektrallinien wird durch die Saha-Gleichung bestimmt:
ne
nn
3
≈ 1.9 × 1015 Tne2 exp(− UTion )
Hierbei ist ne die Elektronendichte, nn die Neutralgasdichte, T die Temperatur und Uion die Ionisationsenergie des betrachteten Elementes. Aus der Besetzungsdichte lassen sich Absorptionskoeffizienten berechnen
und mit deren Hilfe schließlich das Profil der Spektrallinie (D. Koester 2001). Die bekannteste Klassifikation
ist die ”Harvard-Klassifikation”, welche Ende des 19. Jahrhunderts entwickelt wurde:
O, B, A, F, G, K, M
Dabei sind O-Sterne am heißesten, während die M-Sterne relativ kühl sind. Die Merkmale der unterschiedlichen Spektraltypen von O bis M sind in Tabelle 6.2 zusammengestellt.
Spektraltyp
Temperatur [K]
Klassifikationsmerkmale
O
50000
Linien hochionisierter Atome: He II, Si IV, N
III,...; Wasserstoff H relativ schwach.
B0
25000
He II fehlt; He I stark; Si III, O II; H stärker.
A0
10000
He I fehlt; H im Maximum; Mg II, Si II, stark; Fe
II, Ti II schwach; Ca II schwach.
F0
7600
H schwächer; Ca II stark; die ionisierten Metalle,
z.B. Fe II, Ti II hatten ihr Maximum bei A5; die
neutralen Metalle erreichen nun etwa die gleiche
Stärke.
G0
6000
Ca II sehr stark; neutrale Metalle Fe I, ... sehr
stark.
K0
5100
H relativ schwach, neutrale Atomlinien stark; Molekülbanden.
M0
3600
Neutrale Atomlinien , z.B. Ca I, sehr stark; TiOBanden.
Tabelle 6.2. Klassifikation der Spektraltypen (modifizert aus Unsöld, Baschek (2002))
36
Aufnahme von Sternspektren
6.2.2 Aufnahme und Bearbeitung der Sternspektren
Für die Darstellung der Spektraltypen wurden sieben Sterne des Sommerhimmels ausgewählt (Tabelle 7.2).
Von diesen wurden am Abend des 10.10.2004 zwischen 21:40 Uhr und 23:45 Uhr MESZ bei guten Seeingbedinungen (R = 2,D = 3) im Ritchey-Chrétien-Fokus niedrigaufgelöste Spektren aufgenommen. Die Belichtungszeit lag dabei, je nach Helligkeit des Sterns, zwischen 60 und 180 Sekunden. Für die spätere
Wellenlängenkalibration wurden zu jedem Sternspektrum 20 Sekunden belichtete Aufnahmen einer HgDampflampe erstellt. Nach dem Abzug eines Dunkelbildes wird das Spektrum ausgewertet.
Stern
Spektraltyp
Schraubenwert
HD 193322
O9
5.4
η UMa
B3
5.4
² UMa
A0
5.4
δ Aql
F3
5.4
β Aql
G8
5.4
γ Aql
K3
5.4
² Del
M6
5.4
Tabelle 6.3. Liste der spektroskopierten Sterne, sowie der am Spektrographen eingestellte Schraubenwert bei
niedriger Auflösung.
6.2.3 Auswertung der Sternspektren
Nach der Konvertierung der ST7-Dateien ins FITS-Format kann die Wellenlängenkalibration vorgenommen
werden. Dazu wurde das Midas-Skript ”spect.prg” verwendet. Durch Auswahl von zwei Eichlinien wird
die Dispersionskurve berechnet und das Spektrum als Zeilenscan ausgegeben. Zur Wellenlängenkalibration
wurden die Hg-Linien bei 546.1 und 577.0 nm verwendet.
6.2 Sequenz der Spektraltypen von O bis M
37
6.2.4 Ergebnisse
Nach der Bearbeitung der Rohaufnahmen werden die Spektrallinien mit Hilfe des Programmes VisualSpec
von Valerie Desnoux identifiziert. Dieses beinhaltet eine Datenbank aller chemischen Elemente bis einschließlich Eisen, sowie einige Molekülbanden.
6.2.4.1 HD 193322
Die Balmerlinien Hβ, ist schwach erkennbar. Daneben sind einige O II-Linien sowie eine He II-Linie
sichtbar.
6.2.4.2 η UMa
Im Spektrum dieses B Sterns treten die Balmerlinien Hβ und Hγ bereits deutlich hervor. Daneben finden
sich He I, O II und Si III Linien.
6.2.4.3 ² UMa
Das Spektrum wird von den Balmerlinien Hβ bis Hη dominiert.
6.2.4.4 δ Aql
Neben den, im Vergleich zu dem A Stern ² UMa schwächeren Balmerlinien, ist auch die Ca II Linie erkennbar.
6.2.4.5 β Aql
Die Balmerlinien sind, bis aus Hβ und Hγ nur noch schwach erkennbar. Neben den gut erkennbaren Ca IILinien findet sich eine Linie des neutralen Metalls Eisen F e I.
6.2.4.6 γ Aql
Die Balmerlinien sind kaum erkennbar. Die Banden des Titanoxid-Moleküls T iO sind bereits gut sichtbar.
Daneben beherrschen neutrale Atomlinien das Spektrum: Ca I, O I.
6.2.4.7 ² Del
Am deutlichsten sind die T iO-Banden ausgeprägt. Die Balmerlinien sind hingegen verschwunden.
OII
H
β
Aufnahme von Sternspektren
OII
38
Abb. 6.1. Spektrum des O Sterns HD 193322.
39
HεHδ
Hγ
He I
H
β
6.2 Sequenz der Spektraltypen von O bis M
Abb. 6.2. Spektrum des B Sterns η UMa
Aufnahme von Sternspektren
Ηη
Ηζ
Η
Ηε
δ
Ηγ
Ηβ
40
Abb. 6.3. Spektrum des A Sterns ² UMa
Ca II
H
ζ
Hη
H
δ
H
γ
H
β
6.2 Sequenz der Spektraltypen von O bis M
Abb. 6.4. Spektrum des F Sterns δ Aql
41
Fe I ?
H
β
Aufnahme von Sternspektren
Ca II
Hγ
42
Abb. 6.5. Spektrum des G Sterns β Aql
43
Abb. 6.6. Spektrum des K Sterns γ Aql
Ca I
TiO
TiO
CaI
OI
TiO
TiO
6.2 Sequenz der Spektraltypen von O bis M
TiO
TiO
Aufnahme von Sternspektren
TiO
TiO
44
Abb. 6.7. Spektrum des M Sterns ² Del
7
Spektralanalyse von BD+33◦2642
Am Beispiel des Sterns BD+33◦ 2642 soll die Analyse eines hochaufgelösten Sternspektrums demonstriert
werden. Das optische Spektrum, welches hier verwendet wird, ist am Calar Alto Observatorium in Spanien
mit einem 3.5-Meter-Teleskop gewonnen worden.
7.1 BD+33◦ 2642
BD+33◦ 2642 ist ein blauer Stern (Post-AGB-Stern), der sich bei relativ hohen galaktischen Breiten befindet
(b = 50.8◦ ). Er ist der Zentralstern eines planetarischen Nebels, welcher einen scheinbaren Durchmesser von
500 besitzt.
7.2 Bestimmung der fundamentalen Sternparameter
Für die Bestimmung von Temperatur und Schwerebeschleunigung wird das Programm ”synspec” verwendet,
welches verschiedene Modelle von Sternatmosphären (Kurucz-Modelle) beinhaltet. Aus diesen Modellatmosphären läßt sich die Form der einzelnen Linien in einem Spektrum aus den in den Modellen verwendeten Parametern wie Druck, Temperatur und Schichtdicke der Atmosphäre berechnen. Erleichtert wird die
Bestimmung der Sternparameter durch das von I. Hubeny geschriebene Programm ”synplot”, einem IDLSkript, welches eine interaktive Anpassung der Linienprofile gestattet. Zur Bestimmung der Sternparameter werden zwei ausgeprägte Spektrallinien mit deutlichem Linienkern und Flügel verwendet, H − β und
H − δ. Da Wasserstoff das häufigsten Element in einem Stern ist, spielt die Elementhäufigkeit keine Rolle. Ausgangspunkt sind die in dem Artikel von Napiwotzki et al. gefundenen Parameter für BD+33◦ 2642:
T = 20000 K, log g = 2.9. Die Kurucz-Modelle beinhalten nur Sternatmosphären mit einer Schwerebeschleunigung von log g = 3.0 und aufwärts. Als erstes wird die ausgeprägte H − β-Linie gefittet: Bei einer
Temperatur von 20000 K und log g = 3.5 ergeben sich zu schmale Linienflügel (Abbildung 7.1). Bei einem
konstanten log g = 3.0 wird deshalb anschließend die Temperatur variiert (Abbildung 7.2 bis 7.2). Der beste
Fit ergibt sich bei T = 21000 K und log g = 3.0. Analog wird die H − δ-Linie gefittet. Das Ergebnis zeigt
Abbildung 7.6.
45
46
Spektralanalyse von BD+33◦ 2642
Abb. 7.1. Hβ-Linie bei T = 20000 K, log g = 3.5
7.2 Bestimmung der fundamentalen Sternparameter
Abb. 7.2. Variation der Effektivtemperatur bei log g = 3.0, T = 20000 K
47
48
Spektralanalyse von BD+33◦ 2642
Abb. 7.3. T = 21000 K
7.2 Bestimmung der fundamentalen Sternparameter
Abb. 7.4. T = 22000 K
49
50
Spektralanalyse von BD+33◦ 2642
Abb. 7.5. T = 23000 K
7.2 Bestimmung der fundamentalen Sternparameter
Abb. 7.6. Hδ-Linie bei T = 21000 K, log g = 3.0
51
52
Spektralanalyse von BD+33◦ 2642
7.3 Elementhäufigkeiten
Nach der Bestimmung von Temperatur und Schwerebeschleunigung können die Häufigkeiten der Elemente
He, C, M g, N , O, Si ermittelt werden. Für He ergibt sich der beste Fit bei einer solaren Häufigkeit: In
Abbildung 7.7 ist die He − II-Linie bei 438.7 nm mit 35% solarer Häufigkeit dargestellt. Zum Vergleich
zeigt Abbildung 7.8 das Linienprofil mit solarer Häufigkeit. Für die untersuchten ”Metalle” (alle Elemente
außer H und He) zeigt sich, daß diese im Vergleich zur Sonne stark verarmt sind. Für die Elemente O
und N konnten drei Linien im Spektrum gefittet werden. Für die anderen Elemente konnte nur jeweils
eine Linie zur Bestimmung der Elementhäufigkeit herangezogen werden. Die Ergebnisse sind in Tabelle 7.2
zusammengestellt.
7.4 Vergleich mit der Arbeit von Napiwotzki et al.
Der Vergleich der Ergebnisse mit den Literaturwerten zeigt, daß bei allen Elementen, mit Ausnahme von
C und He die Elementhäufigkeiten kleiner sind als die Literaturwerte. Die Standardabweichung der hier
durchgeführten Messungen scheint kleiner zu sein. Ein direkter Vergleich ist jedoch nicht möglich, da den
Literaturwerten wesentlich mehr Datenmaterial zugrundeliegt. Es umfaßt neben dem optischen auch den
UV-Bereich des Spektrums. Entsprechend konnte in der Arbeit von Napiwotzki mehr Linien ausgemessen
und damit eine bessere Statistik betrieben werden.
7.4 Vergleich mit der Arbeit von Napiwotzki et al.
Element
Wellenlänge (nm)
[El/H]
C II
426.7
0.07
N II
460.7
0.32
460.1
0.25
463.0
0.34
463.8
0.28
466.1
0.30
464.1
0.33
Mg II
448.1
0.34
Si II
413.0
0.37
He I
438.7
1.0
O II
Tabelle 7.1. Verwendete Spektrallinien und Elementhäufigkeiten
Element
log[El/H]
log[El/H]N apiwotzki
C II
-1.3
-1.1 ± 0.4
N II
-0.5 ± 0.07
-0.7 ± 0.4
O II
-0.54 ± 0.061
-0.8 ± 0.4
Mg II
-0.5
-1.1 ± 0.3
Si II
-0.5
-0.9 ± 0.3
He I
0.0
0.0 ± 0.1
Tabelle 7.2. Vergleich der bestimmten Elementhäufigkeiten mit denen von Napiwotzki et al.
53
54
Spektralanalyse von BD+33◦ 2642
Abb. 7.7. Modell Helium-Linie mit 0.35× solarer Häufigkeit im Vergleich mit der gemessenen Heliumlinie. Man
beachte den Misfit.
7.4 Vergleich mit der Arbeit von Napiwotzki et al.
Abb. 7.8. Gefittete Helium-Linie mit solarer Häufigkeit
55
56
Spektralanalyse von BD+33◦ 2642
Abb. 7.9. Gefittete Kohlenstoff-II-Linie
7.4 Vergleich mit der Arbeit von Napiwotzki et al.
Abb. 7.10. Gefittete Magnesium-II-Linie
57
58
Spektralanalyse von BD+33◦ 2642
Abb. 7.11. Gefittete Stickstoff-II-Linie
7.4 Vergleich mit der Arbeit von Napiwotzki et al.
Abb. 7.12. Gefittete Sauerstoff-II-Linie
59
60
Spektralanalyse von BD+33◦ 2642
Abb. 7.13. Gefittete Silicium-II-Linie
Anhang 1
Das Midas-Skript ”phot.prg”
define/local low/r/1/1 0.
define/local high/r/1/1 0.
define/local maxrad/r/1/1 14.
define/local max/r/1/1 14.
define/local schritt/r/1/1 1.
define/local refmag/r/1/1 0.
define/local xoff/r/1/1 0.
define/local yoff/r/1/1 0.
define/local vobs/r/1/1 0.
define/local vlit/r/1/1 0.
define/local voff/r/1/1 0.
define/local bobs/r/1/1 0.
define/local blit/r/1/1 0.
define/local boff/r/1/1 0.
define/local eichnum/i/1/1 0.
define/local xlim/r/1/2 0.,0.
define/local ylim/r/1/2 0.,0.
define/param p1 ? c "Name der V-Aufnahme?"
define/param p2 ? c "Name des V-Flatfield?"
define/param p3 ? c "Name der B-Aufnahme?"
define/param p4 ? c "Name des B-Flatfield?"
define/param p5 ? c "Name der Ergebnis Tabelle (ohne . im Namen!)"
! Umwandeln der Daten von FITS in MIDAS .bdf-Format
! indisk/fits ’FITS-file’ ’.bdf-file’
indisk/fits {p1} vraw
indisk/fits {p2} vff
indisk/fits {p3} braw
indisk/fits {p4} bff
! Fenster erzeugen zur Darstellung 2-dimensionaler Aufnahmen
! create/display Kanal-Nummer Anzahl_pixel_x-Achse, Anzahl_pixel_y-Achse
crea/disp 0 765,510
! Laden einer Tabelle, die Flusswerten Farben zuordnet
! (sog. LookUpTable = LUT)
! load/lut ’Name der LUT’
load/lut heat
! Aufziehen des Flatfields
load/ima vff
! Bestimmen des Maximumswertes fuer die Darstellung
61
62
Das Midas-Skript ”phot.prg”
stat/ima vraw
comp/key max = {outputr(3)}+5*{outputr(4)}
! Aufziehen der Sternhaufenaufnahme mit Minimuswert der Darstellung=0
! und Maximumswert={max}
load/ima vraw cuts=0,{max}
write/out "Normieren der Flatfields"
! Statistik des Flatfields
stat/ima vff
! Normieren des Flatfields (Division durch mittleren Fluss)
! compute/image ’Ergebnis’=’Operation’
comp/ima vff = vff/{outputr(3)}
! Gleiche Prozedur fuer B-Flatfield
stat/ima bff
comp/ima bff = bff/{outputr(3)}
! Flatfieldkorrektur der Sternhaufenaufnahmen
write/out "Flatfieldkorrektur der Sternhaufenaufnahme"
! comp/ima v = vraw/vff
! comp/ima b = braw/bff
! comp/ima v = vraw
! comp/ima b = braw
! Bestimmen des Maximumswertes fuer die Darstellung
stat/ima v
comp/key max = {outputr(3)}+5*{outputr(4)}
load/ima v cuts=0,{max}
!
!
!
!
!
!
Fadenkreuz zur Bestimmung von Flusswerten im dargestellten Bild
write/out "Hintergrundshelligkeit und Helligkeit heller Sterne bestimmen"
write/out "Hintergrundshelligkeit und Helligkeit heller Sterne bestimmen"
write/out "linke Maustaste --> Messung"
write/out "rechte Maustaste --> Verlassen des Cursors"
get/curs
!
!
!
!
inquire/key low "Helligkeit des Hintergrunds?"
inquire/key high "Helligkeit heller Sterne?"
Aufziehen der Sternhaufenaufnahme mit neuen Grenzwerten der Darstellung
load/ima v cuts={low},{high}
write/out "Positionsbestimung der Sterne in der Haufenaufnahme"
write/out "Positionen werden in Tabelle v.tbl gespeichert unter Spalten"
write/out ":xcen und :ycen"
! Positionsbestimmung der Sterne in der Haufenaufnahme
! Positionen werden in Tabelle ngc654v2.tbl gespeichert unter Spalten
! :xcen und :ycen
write/out "Zur Vermessung dient ein Fenster, dessen Groesse "
write/out "mit den Pfeiltasten der Tastatur angepasst werden kann. "
Das Midas-Skript ”phot.prg”
! Zur Vermessung dient ein Fenster, dessen Groesse mit den Pfeiltasten
! der Tastatur angepasst werden kann.
! center/gauss ’Methode’ ’Ausgabetabelle’
center/gauss cursor v
! Markieren der zu vermessenden Sterne
! load/tab ’Tabelle’ ’x-Position’ ’y-Position’ ’Identifikation’
! Symboltyp Symbolgroesse ’Symbolfarbe’ Verbindung_der_Symbole
load/tab v :xcen :ycen :ident 1 3 green 0
write/out "Tabelle v.tbl wird nach v_in.tbl kopiert"
! Kopieren der Tabelle ngc654v2.tbl nach ngc654v2in.tbl
copy/tab v v_in
write/out "Spalten :xcen und :ycen werden in :x_coord und :y_coord umbenannt"
! Umbenennen der Spalten fuer die Eingabe in integrate/star
! name/column ’Tabelle’ ’alter Name’ ’neuer Name’
name/col v_in :xcen :x_coord
name/col v_in :ycen :y_coord
write/out "Integration des Sternenflusses in einer angepassten Blende und"
write/out "Korrektur des Hintergrundes"
write/out "Ergebnis steht in v_out.tbl"
! Integration des Sternenflusses in einer angepassten Blende und
! Korrektur des Hintergrundes
! integr/star ’Aufnahme, Eingabetabelle’ ’Ausgabetabelle’
! Maximalradius_der_Blende, Schrittweite_bei_Radiusanpassung, Referenzhelligkeit
inquire/key maxrad "Maximalradius der Blende (Standardwert = 14.)?"
integrate/star v,v_in v_out {maxrad},1,0
! Bestimmen des Maximumswertes fuer die Darstellung
stat/ima b
comp/key max = {outputr(3)}+5*{outputr(4)}
! Aufziehen der B-Aufnahme des Sternhaufens
load b cuts=0,{max}
! Positionsmarkierungen der V-Aufnahme bleiben erhalten!
write/out "Vermessen Sie einige in der V-Aufnahme vermessene Sterne"
write/out "in der B-Aufnahme. Die Ergebnisse erscheinen nur am Bildschirm"
! Einige in der V-Aufnahme vermessene Sterne in der B-Aufnahme vermessen
! Ausgabe der Ergebnisse nur auf dem Bildschirm
center/gauss cursor
!ngc654v2 ID0001 <--> ID0002 ngc654b2
!
0003
0003
!
0011
0001
write/out "Aus dem Vergleich der Positionen ergibt sich der Versatz."
write/out "zwischen V- und B-Aufnahme"
write/out "read/tab v gibt den Inhalt der Tabelle v zum Vergleich mit den"
write/out "Messwerten aus"
read/tab v
! Aus dem Vergleich der Positionen ergibt sich
! x_b2 = x_v2-5.09
63
64
Das Midas-Skript ”phot.prg”
! y_b2 = y_v2-6.46
inquire/key xoff "Versatz in x-Richtung (x_v - x_b)?"
inquire/key yoff "Versatz in y-Richtung (y_v - y_b)?"
write/out "Tabelle v.tbl wird nach b_in.tbl kopiert"
! Kopieren der Tabelle v.tbl nach b_in.tbl
copy/tab v b_in
write/out "Korrektur des Versatz zwischen V- und B-Aufnahme in Tabelle b_in.tbl"
! Korrektur der Position fuer Eingabe in integrate/star
! compute/table ’Tabelle’ ’Ergebnisspalte’ = ’Operation’
comp/tab b_in :x_coord = :xcen-{xoff}
comp/tab b_in :y_coord = :ycen-{yoff}
write/out "test"
clear/chan o
! Markieren der vermessenen Sterne in der B-Aufnahme
load/tab b_in :x_coord :y_coord :ident 1 3 blue 0
write/out "Integration des Sternflusses in einer angepassten Blende und"
write/out "Korrektur des Hintergundes"
write/out "Ergebnis steht in b_out.tbl"
! Messung des Sternflusses in der B Aufnahme
integrate/star b,b_in b_out {maxrad},1,0
write/out "Eichstern aus der Literaturarbeit identifizieren durch Vergleich"
write/out "der Aufnahme und der Sucherkarte"
! Sterne 2 und 97 aus der Literaturarbeit auswaehlen durch Vergleich
! der Aufnahme und der Sucherkarte
! select/table ’Tabelle’ ’Selektionskriterium’
inquire/key eichnum "Nummer des Eichsterns bei der Vermessung (z.B.5)?"
inquire/key vlit "V-Helligkeit des Eichsterns?"
write/out "Nullpunkte berechnen und anbringen"
write/key vobs {v_out,:magnitude,@{eichnum}}
comp/key voff = vlit-vobs
comp/tab v_out :V = :magnitude+{voff}
inquire/key blit "B-Helligkeit des Eichsterns?"
write/key bobs {b_out,:magnitude,@{eichnum}}
comp/key boff = blit-bobs
comp/tab b_out :B = :magnitude+{boff}
copy/tab v_out {p5}
copy/tt b_out :B {p5} :B
! B-V ausrechnen
comp/tab {p5} :B_V = :B-:V
! Farben-Helligkeitsdiagramm darstellen
! x- und y-Achse setzen
stat/tab {p5} :B_V
write/key xlim/r/1/2 {outputr(1)},{outputr(2)}
stat/tab {p5} :V
write/key ylim/r/1/2 {outputr(1)},{outputr(2)}
crea/graph
Das Midas-Skript ”phot.prg”
set/graph xaxis={xlim(1)},{xlim(2)} yaxis={ylim(1)},{ylim(2)}
!plot/tab ’Tabelle’ ’x_Achse’ ’y-Achse’
plot/table {p5} :B_V :V
copy/graph postscript
$ mv postscript.ps {p5}.ps
write/out "postscript file = {p5}.ps"
65
Anhang 2
Das Midas-Skript ”Spect.prg”
define/local posspec/r/1/2 0.,0.
define/local skypos/r/1/4 0.,0.,0.,0.
define/local wlc1x/r/1/1 0.
define/local wlc1l/r/1/1 0.
define/local wlc2x/r/1/1 0.
define/local wlc2l/r/1/1 0.
define/local step/r/1/1 0.
define/local plot/c/1/1 "y"
define/param p1 ? c "Sternspektrum (fits-Format)?"
define/param p2 ? c "Dark fuer das Sternspektrum ?"
define/param p3 ? c "Wellenlaengenkalibrationsspektrum (fits-Format) ?"
define/param p4 ? c "Name fuer das Ergebnis (ohne . im Filenamen)"
set/grap pmod=1
indisk/fits {p1} specraw
indisk/fits {p3} wlc
crea/grap
if p2(1:2) .ne. "no" then
indisk/fits {p2} dark
comp spec = specraw-dark
else
comp spec = specraw
endif
aver/col specpos = spec <,>
plot specpos
write/out "Bereich des Sternspektrums und des Himmelshintergunds bestimmen"
write/out "Linke Maustaste --> Position"
write/out "Rechte Maustaste --> Verlassen des Cursor-Programms"
write/out "2 Positionen fuer Sternspektrum, 2 fuer Himmelshintergund"
!write/out "rechts und links vom Sternspektrum"
get/gcurs
inquire/key posspec "Bereich des Sternspektrums (2 Zahlen, durch Komma getrennt)"
inquire/key skypos "Bereich des Himmelshintergrunds (2 Zahlen, durch Komma getrennt)"
aver/row raw = spec {posspec(1)},{posspec(2)}
aver/row sky = spec {skypos(1)},{skypos(2)}
aver/row wlcraw = wlc {posspec(1)},{posspec(2)}
aver/row wlcsky = wlc {skypos(1)},{skypos(2)}
plot wlcraw
write/out "Position zweier Kalibrationslinien bestimmen"
get/gcurs
inquire/key wlc1x "X-Position der linken Kalibrationslinie?"
inquire/key wlc1l "Wellenlaenge der linken Kalibrationslinie?"
inquire/key wlc2x "X-Position der rechten Kalibrationslinie?"
66
Das Midas-Skript ”Spect.prg”
inquire/key wlc2l "Wellenlaenge der rechten Kalibrationslinie?"
copy/it raw raw :x
comp/tab raw :lambda = (:x-{wlc1x})/({wlc2x}-{wlc1x})*({wlc2l}-{wlc1l})+{wlc1l}
plot wlcsky
write/out "Position der beiden Kalibrationslinien bestimmen"
get/gcurs
inquire/key wlc1x "X-Position der linken Kalibrationslinie?"
inquire/key wlc2x "X-Position der rechten Kalibrationslinie?"
copy/it sky sky :x
comp/tab sky :lambda = (:x-{wlc1x})/({wlc2x}-{wlc1x})*({wlc2l}-{wlc1l})+{wlc1l}
sort/tab raw :lambda
sort/tab sky :lambda
stat/tab raw :lambda
comp/key step = ({outputr(2)}-{outputr(1)})/765
crea/ima ref 1,765 {outputr(1)},{step} nodata
convert/tab rawlam = raw :lambda #2 ref spline
convert/tab skylam = sky :lambda #2 ref spline
comp/ima {p4} = rawlam-skylam
plot {p4}
inquire/key plot " postscript file erzeugen?"
if plot(1:1) .eq. "y" then
copy/grap postscript
$ mv postscript.ps {p4}.ps
write/out "postscript file = {p4}.ps"
endif
outdisk/fits {p4}.bdf {p4}.fits
67
Literatur
Anleitung zum FP IIe: Astronomie und Spektroskopie, Wintersemester 2001/02, Institut für Theoretische Physik
und Astrophysik, CAU Kiel
R. Napiwotzki et al. 1994, ”Analysis of BD+33◦ 2642: a newly detected planetary nebula in the galactic halo and its
central star”, Astron. Astophys. 292, 239-248
Beatty, Petersen, Chaikin, ” The New Solar System ”, Cambridge University Press 1999
Unsöld, Baschek, Der neue Kosmos, Springer Verlag 2002
http://ngala.as.arizona.edu/dennis/instruct/ay14
Phelps R.L., Janes K.A. 1994, APJS 90, 31
G.D.Roth (Hrsg.), ”Planeten beobachten”, Verlag Sterne und Weltraum 1998
Jean Lacroux, Christian Legrand, ”Der Kosmos Mondführer”, Kosmos-Verlag 2000
http://dvaa.org/servlets/Sac?item=NGC654
www.sbig.com
Valerie Desnoux: ”VisualSpec” erhältlich für Windows unter http://valerie.desnoux.free.fr/vspec/
D.Koester: ”Stellar Astrophysics I: Stellar Atmospheres”, Third Edition Kiel 2001
D.Koester: ”Sternaufbau und Sternentwicklung”, Kiel 2001
68