Abiturprüfung 2007
Werbung

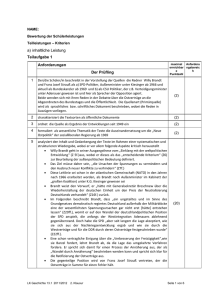
Ministerium für Schule und Weiterbildung NRW PH GK HT 1 Seite 1 von 12 Unterlagen für die Lehrkraft Abiturprüfung 2007 Physik, Grundkurs 1. Aufgabenart Bearbeitung eines Demonstrationsexperiments Bearbeitung einer Aufgabe, die fachspezifisches Material enthält 2. Aufgabenstellung Aufgabe 1: Ablenkung elektrisch geladener Teilchen in elektrischen und magnetischen Feldern (55 Punkte) Aufgabe 2: Wasserstoffspektrum und Bohr’sches Atommodell 3. (51 Punkte) Materialgrundlage Hinweise zum Experiment in Aufgabe 2: Das vom Lehrer zu Beginn der Bearbeitung durchgeführte Experiment bleibt während der gesamten Bearbeitungszeit aufgebaut stehen. Versuchsaufbau1: Versuchsdurchführung: Das Linienspektrum von Wasserstoff wird mit oben abgebildetem Aufbau (Kondensorlinse f = 50 mm, verstellbarer Spalt, Abbildungslinse f = 20 cm oder f = 10 cm und RowlandGitter-Kopie mit 570 Strichen pro mm) auf eine Leinwand oder einen Schirm abgebildet. Die Distanz e (Entfernung Gitter-Schirm) ist je nach lokalen Gegebenheiten und Präsentationsmöglichkeit der Messwerte zwischen 1 m und 3 m zu wählen. Die Brennweite der Abbildungslinse ist entsprechend anzupassen. 1 Vgl. Bader, F.: Dorn-Bader Physik 12/13, Gymnasium Sek II, Hannover 2000, S. 188; die Skizze wurde abgeändert Nur für den Dienstgebrauch! Ministerium für Schule und Weiterbildung NRW PH GK HT 1 Seite 2 von 12 Der Abstand a des 1. Maximums der roten Wasserstofflinie von der Mitte sowie der Abstand e zwischen Gitter und Schirm werden gemessen und den Schülerinnen und Schülern mitgeteilt. Kann der Versuch nicht durchgeführt werden oder misslingt er, werden den Schülerinnen und Schülern folgende Messwerte zur Verfügung gestellt: Abstand des Maximums 1. Ordnung der roten Linie von der Mitte a = 60,0 cm; Abstand Gitter/Schirm e = 150 cm. 4. Bezüge zu den Vorgaben 2007 1. Inhaltliche Schwerpunkte Aufgabe 1: Ladungen und Felder – Elektrisches Feld, elektrische Feldstärke – Magnetisches Feld, magnetische Feldgröße B, Lorentzkraft – Bewegung von Ladungsträgern in elektrischen und magnetischen Feldern Aufgabe 2: Elektromagnetische Schwingungen und Wellen – Interferenz (Lichtbeugung am Spalt, Doppelspalt und Gitter, Wellenlängenmessung) Atom- und Kernphysik – Linienspektren und Energiequantelung des Atoms, Atommodelle (Beobachtung von Spektrallinien am Gitter) 2. Medien/Materialien – entfällt 5. Zugelassene Hilfsmittel – Physikalische Formelsammlung – Wissenschaftlicher Taschenrechner (ohne oder mit Grafikfähigkeit) – Wörterbuch zur deutschen Rechtschreibung 6. Vorgaben für die Bewertung der Schülerleistungen 6.1 Modelllösungen Hinweis für die korrigierende Lehrkraft: Die nachfolgenden Beispiellösungen erfassen nicht notwendigerweise alle sachlich richtigen Lösungsalternativen. Aufgabe 1: Ablenkung elektrisch geladener Teilchen in elektrischen und magnetischen Feldern a) 1. Das (positiv geladene) Proton erfährt eine konstante elektrische Feldkraft und wird in Richtung der elektrischen Feldlinien gleichmäßig beschleunigt, sodass die vertikale Geschwindigkeitskomponente linear mit der Zeit ansteigt, die horizontale Komponente aber konstant bleibt. Das Proton läuft daher auf einer nach unten geöffneten Parabelbahn. Nur für den Dienstgebrauch! PH GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 3 von 12 2. Das (negativ geladene) Elektron erfährt im Magnetfeld eine Lorentzkraft jederzeit senkrecht zu seiner Bewegungsrichtung, sodass sich seine Bahngeschwindigkeit nicht verändert. Die Lorentzkraft wirkt als eine Zentralkraft, sodass sich als Bewegungsform eine Kreisbahn ergibt. 3. Das (zweifach positiv geladene) α-Teilchen wird parallel zu den elektrischen Feldlinien durch die elektrische Feldkraft beschleunigt. Seine Geschwindigkeit steigt linear mit der Zeit an, es handelt sich um eine gleichmäßig beschleunigte Bewegung. Es durchläuft das elektrische Feld geradlinig (ohne Ablenkung). 4. Das positiv geladene Ion erfährt nach der Lorentzkraft bei einer Bewegung parallel zu den magnetischen Feldlinien keine Kraft, sodass es sich mit der konstanten Eintrittsgeschwindigkeit geradlinig gleichförmig weiterbewegt. b) In y-Richtung erfahren die Elektronen im homogenen Querfeld des Kondensators eine konstante elektrische Kraft nach oben, sodass sie eine gleichmäßig beschleunigte Bewegung ausführen. Daher gilt: 1 y = ay ⋅ t 2 . 2 Mit Fy = m ⋅ ay , E = Es ist also: y = Fy e und E = Uy d errechnet sich ay zu: ay = Fy m = e ⋅ E e Uy = ⋅ . m m d 1 e Uy 2 ⋅ ⋅t . 2m d In x-Richtung führen die Elektronen eine gleichförmige Bewegung aus, für die das Zeit-Weg-Gesetz lautet: x = v 0 ⋅ t . Die Bewegungen in x- und y-Richtung überlagern sich ungestört; daher ergibt sich durch Eliminieren von t: y= 1 e Uy 1 2 ⋅ ⋅ ⋅x . 2 m d v02 Die Kondensatoreintrittsgeschwindigkeit der Elektronen nach dem Passieren der Beschleunigungsstrecke ergibt sich aus: e ⋅ U A = Eel = Ekin = 21 m ⋅ v 02 . Damit lässt sich v02 bestimmen zu v 02 = 2 e ⋅ UA . m Damit erhält man für die Bahnkurve letztlich die Gleichung: y= 1 Uy 1 e Uy 1 2 1 e Uy 1 ⋅ ⋅ 2 ⋅x = ⋅ ⋅ ⋅ x2 = ⋅ ⋅x2 4d U A 2 m d v0 2 m d 2 e ⋅U m A Nur für den Dienstgebrauch! PH GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 4 von 12 c) Die Anfertigung eines 1 − y -Diagramms ergibt die nachfolgende Grafik: UA 35 30 -3 y in 10 m 25 20 15 10 5 0 0,0 0,2 0,4 0,6 0,8 1,0 1/UA in 1/kV Es ergibt sich (näherungsweise) eine Ursprungsgerade mit der Steigung k1 = y ⋅ U A ≈ 35 V ⋅ m . Mit dem Ergebnis aus Teilaufgabe b und x = 0,15 m folgt für Uy : Uy ≈ 490 V . Hinweis für die korrigierende Lehrkraft: Alternative Lösungswege, wie beispielsweise das Anfertigen eines UA-y-Diagramms, das Vermuten des Vorliegens einer Hyperbel, das Prüfen der Antiproportionalität mit Hilfe der Produktgleichheit bei den Messwertpaaren und die anschließende Weiterverwendung des Mittelwerts der Produkte, sind ebenso möglich wie die Benutzung eines CAS-Systems. d) Die Elektronen treten unter dem Winkel α (≠0°) zur Horizontalen in das parallel zur G x-Achse gerichtete Magnetfeld ein. Der Geschwindigkeitsvektor v lässt sich in eine G G Komponente v s senkrecht zur x-Achse und in eine Komponente vp parallel zur x-Achse zerlegen. G vS G v α G vP Nur für den Dienstgebrauch! G B PH GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 5 von 12 G Die Komponente vp ist parallel zur Richtung des Magnetfelds, daher tritt hier keine Lorentzkraft auf, sodass diese Komponente lediglich eine gleichförmige Bewegung der Elektronen in x-Richtung verursacht. G Die Komponente v s , die senkrecht zur magnetischen Feldstärke gerichtet ist, verursacht die Ablenkung der Elektronen auf eine Kreisbahn, da die hier wirkende LorentzG kraft senkrecht zur Richtung von v s die für die Kreisbewegung notwendige Zentripetalkraft darstellt. Die unabhängige Überlagerung der beiden Bewegungen ergibt eine „in x-Richtung auseinandergezogene Kreisbahn“, d. h. eine Schraubenlinienbahn. Aufgabe 2: Wasserstoffspektrum und Bohr’sches Atommodell a) Parallele Wellenzüge werden am Gitter gebeugt. Die Gitteröffnungen können als Ausgangspunkte phasengleicher Elementarwellen aufgefasst werden. Im Raumpunkt P kommt es zur Überlagerung und Interferenz von N Wellenzügen. Verstärken sich alle zu einer Farbe gehörenden Wellenzüge unter einem Winkel α gegenseitig, so müssen die Wellenzüge benachbarter Gitteröffnungen einen Gangun- J. Grehn, J. Krause: Metzler Physik, 1998. S. 295, Zeichnung leicht abgeändert terschied Δs von genau einem Vielfachen einer Wellenlänge aufweisen. Dies ist nur bei bestimmten Winkeln möglich, weil es aufgrund der großen Anzahl der Gitteröffnungen bereits bei kleinsten Richtungsabweichungen zur Auslöschung der Wellenzüge kommt, da es zu einem beliebigen Wellenzug einen parallel verlaufenden Wellenzug mit einem Gangunterschied von einem ungeradzahligen Vielfachen einer halben Wellenlänge geben wird, sodass sich beide Wellenzüge gegenseitig (mindestens teilweise) auslöschen. Da die verschiedenen Farben des Wasserstofflichts unterschiedliche Wellenlängen haben, sieht man unter jeweils für sie charakteristischen Winkeln ein Helligkeitsmaximum. Die Helligkeitsmaxima erster, zweiter, dritter … Ordnung entstehen, wenn der Gangunterschied zwischen benachbarten Gitteröffnungen das Einfache, Doppelte, Dreifache … der Wellenlänge des Lichts der jeweiligen Farbe beträgt. Nur für den Dienstgebrauch! PH GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 6 von 12 b) Der Winkel αrot für das 1. Maximum der roten Wasserstofflinie ergibt sich aus: tan(αrot ) = a/e , also mit den (in der Aufgabe genannten Ersatz-)Werten aus dem Ex- periment: αrot = 21,8° . Für das 1. Maximum ist der Gangunterschied zwischen benachbarten Gitteröffnungen genau 1⋅λrot, also: sin ( αrot ) = λrot / g , also λrot = g ⋅ sin( αrot ) . Daraus ergibt sich mit den Zahlenwerten: λrot = 1m / 570000 ⋅ sin(21,8°) = 652 nm . c) Nach Balmer ergibt sich für m = 3 (geringstmöglicher Energieübergang auf n = 2, rotes Licht): frot = RH ⋅ ( 41 − 91 ) = 4,57 ⋅ 1014 Hz und somit λrot = c / frot = 656 nm . Das Bohr’sche Atommodell erklärt das Aussenden von Licht (allg. von elektromagnetischer Strahlung) mit dem Übergang eines Hüllenelektrons von einem energetisch höheren auf einen energetisch niedrigeren Zustand, wobei die hierbei auftretende Energiedifferenz ΔE die Energie der elektromagnetischen Strahlung gemäß ΔE = h ⋅ f bzw. ΔE = h ⋅ c / λ darstellt. Für Wasserstoff erhält man beim Übergang vom Zustand mit der Quantenzahl m = 3 in den mit der Quantenzahl n = 2 aus der gegebenen Formel: ΔE = E3 − E2 = − e 4 ⋅ me 8ε 0 2 ⋅ h 2 1 ⎞ e 4 ⋅ me ⎛ 1 − ⎜ 2 ⎟= n 2 ⎠ 8ε 0 2 ⋅ h 2 ⎝m ⎛ 1 1⎞ ⎜ 4 − 9⎟ . ⎝ ⎠ Mit den der Formelsammlung entnommenen Werten der Konstanten ergibt sich: 5 Δ E = 2,18 ⋅ 10 −18 ⋅ 36 J = 3,03 ⋅ 10−18 J . Daraus erhält man für λrot = h ⋅ c / ΔE : λrot = 656 nm . Beide Formeln liefern dieselbe Wellenlänge. d) Im (heißen) atomaren Wasserstoff gibt es angeregte Atome, deren Elektronen sich im Zustand mit n = 2 befinden. Das im Glühlampenlicht vorkommende Licht der Wellenlänge λrot kann diese Elektronen anregen, in den energetisch höheren Zustand mit n = 3 zu wechseln; das jeweilige Lichtquant selbst existiert nach der Wechselwirkung nicht mehr. Anschließend kann das angeregte Elektron in den Zustand mit n = 2 oder auch n = 1 zurückgehen, sodass im ersten Fall Licht der Wellenlänge λrot oder im zweiten Fall UV-Licht ausgesandt wird. Dieses ausgesandte Licht der Wellenlänge λrot wird jedoch in alle Raumrichtungen ausgesandt, sodass auf dem Schirm nur noch vernachlässigbar wenig Licht der Wellenlänge λrot registriert wird, was zu der Intensitätsabschwächung im Spektrum führt. Nur für den Dienstgebrauch! Ministerium für Schule und Weiterbildung NRW PH GK HT 1 Seite 7 von 12 6.2 Teilleistungen – Kriterien a) inhaltliche Leistung Aufgabe 1: Ablenkung elektrisch geladener Teilchen in elektrischen und magnetischen Feldern Teilaufgabe a) Anforderungen Der Prüfling maximal erreichbare Punktzahl (AFB)2 1 erkennt die vorgegebenen Teilchen hinsichtlich der Ladung sowie die Felder hinsichtlich ihrer jeweiligen Richtung. 4 (I) 2 nennt Aussagen zu den auftretenden Kräften in allen vier Fällen. 4 (I) 3 nennt Aussagen zu den Bewegungsarten der Teilchen in allen vier Fällen. 4 (II) 4 beschreibt die Bahnform im E- bzw. B-Feld in allen 4 Fällen. 4 (II) Teilaufgabe b) Anforderungen Der Prüfling maximal erreichbare Punktzahl (AFB) 1 beschreibt die Bewegungsformen der Elektronen in x-Richtung und begründet diese. 3 (I) 2 beschreibt die Bewegungsformen der Elektronen in y-Richtung und begründet diese. 4 (II) 3 gibt den Zusammenhang zwischen v0 und UA an. 3 (I) 4 leitet daraus die zeitunabhängige Bewegungsgleichung der Elektronen her. 4 (II) Teilaufgabe c) Anforderungen Der Prüfling 2 maximal erreichbare Punktzahl (AFB) 1 benutzt zur Argumentation ein Diagramm. 4 (I) 2 begründet die Proportionalität. 4 (II) 3 bestimmt anhand der Auswertung des Diagramms und der gegebenen Gleichung die am Kondensator anliegende Spannung. 5 (II) AFB = Anforderungsbereich Nur für den Dienstgebrauch! Ministerium für Schule und Weiterbildung NRW PH GK HT 1 Seite 8 von 12 Teilaufgabe d) Anforderungen Der Prüfling maximal erreichbare Punktzahl (AFB) 1 erläutert anhand einer Skizze die Zerlegung des Geschwindigkeitsvektors in eine Parallel- und eine Vertikalkomponente. 2 (III) 2 beschreibt für beide Geschwindigkeitskomponenten die jeweilige Bewegungsform. 4 (II) 3 nennt die unabhängige Überlagerung. 2 (I) 4 schlussfolgert daraus als Bahnkurve eine Schraubenlinienbahn. 4 (III) Aufgabe 2: Wasserstoffspektrum und Bohr’sches Atommodell Teilaufgabe a) Anforderungen Der Prüfling maximal erreichbare Punktzahl (AFB) 1 erstellt eine geeignete, für die weiteren Erklärungen aussagekräftige und vollständige Skizze. 4 (I) 2 erklärt die Bedingungen für die konstruktive Interferenz (für das Vorliegen der Maxima) am Ort des Schirms. 3 (I) 3 erklärt die Bedingungen für die destruktive Interferenz (für die Bereiche schwacher Intensität) zwischen den Maxima. 3 (II) 4 gibt Aussagen an zu der Lage der Maxima verschiedener Farben (derselben Ordnung). 3 (II) 5 gibt Aussagen an zu der Lage der Maxima unterschiedlicher Ordnung (derselben Farbe). 3 (II) Teilaufgabe b) Anforderungen Der Prüfling maximal erreichbare Punktzahl (AFB) 1 berechnet den Winkel αrot aus den gegebenen Größen a und e. 2 (I) 2 gibt den Gangunterschied zwischen benachbarten Gitteröffnungen für das 1. Maximum an. 2 (I) 3 stellt eine Beziehung zwischen αrot, g und λrot auf. 3 (II) 4 berechnet mit Hilfe des errechneten Winkels αrot die Wellenlänge λrot. 4 (I) Nur für den Dienstgebrauch! Ministerium für Schule und Weiterbildung NRW PH GK HT 1 Seite 9 von 12 Teilaufgabe c) Anforderungen Der Prüfling 1 maximal erreichbare Punktzahl (AFB) nennt den hier relevanten Übergang von m = 3 auf n = 2. 2 (I) berechnet mit Hilfe der Balmerformel und der Beziehung λrot = c/frot die Wellenlänge 4 (II) 3 nennt die Gleichung zur Berechnung der Wellenlänge λrot aus der Energiedifferenz E3 – E2. 3 (I) 4 führt die Rechnung mit den aus der Formelsammlung entnommenen Werten unter Berücksichtigung der Einheitenumrechnung aus. 6 (II) 2 λrot. Teilaufgabe d) Anforderungen Der Prüfling maximal erreichbare Punktzahl (AFB) 1 begründet, dass in (heißem) Wasserstoff Atome im Anregungszustand n = 2 vorhanden sind, die von Licht geeigneter Energie (Frequenz) in den Anregungszustand n = 3 gehoben werden können. 3 (III) 2 erklärt, dass beim Zurückfallen dieser angeregten Wasserstoffatome in einen niedrigeren Energiezustand Licht der Wellenlänge λrot zu allen Seiten ausgesandt wird. 3 (II) 3 begründet, dass aufgrund der in alle Raumrichtungen verteilten Aussendung des Lichts der angeregten Wasserstoffatome im Lichtweg des ankommenden Glühlampenlichts vergleichsweise sehr wenig Licht dieser Frequenz mehr wahrgenommen wird, sodass im Spektrum eine Abschwächung der Intensität wahrgenommen wird. 3 (III) Nur für den Dienstgebrauch! PH GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 10 von 12 7. Bewertungsbogen zur Prüfungsarbeit Name des Prüflings:____________________________________ Kursbezeichnung:____________ Schule: _____________________________________________ Aufgabe 1: Ablenkung elektrisch geladener Teilchen in elektrischen und magnetischen Feldern Teilaufgabe a) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl (AFB) 1 erkennt die vorgegebenen … 2 nennt Aussagen zu … 4 (I) 3 nennt Aussagen zu … 4 (II) 4 beschreibt die Bahnform … 4 (II) 3 EK ZK DK 4 (I) Teilaufgabe b) Anforderungen Lösungsqualität Der Prüfling 1 maximal erreichbare Punktzahl (AFB) beschreibt die Bewegungsformen … 3 (I) 2 beschreibt die Bewegungsformen … 4 (II) 3 gibt den Zusammenhang … 3 (I) 4 leitet daraus die … 4 (II) EK ZK DK Teilaufgabe c) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl (AFB) 1 benutzt zur Argumentation … 4 (I) 2 begründet die Proportionalität. 4 (II) 3 bestimmt anhand der … 5 (II) EK ZK DK Teilaufgabe d) Anforderungen Lösungsqualität Der Prüfling 1 erläutert anhand einer … 2 (III) 2 beschreibt für beide … 4 (II) 3 nennt die unabhängige … 2 (I) 4 schlussfolgert daraus als … 4 (III) Summe 1. Aufgabe 3 maximal erreichbare Punktzahl (AFB) 55 EK = Erstkorrektur; ZK = Zweitkorrektur; DK = Drittkorrektur Nur für den Dienstgebrauch! EK ZK DK PH GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 11 von 12 Aufgabe 2: Wasserstoffspektrum und Bohr’sches Atommodell Teilaufgabe a) Anforderungen Lösungsqualität Der Prüfling 1 erstellt eine geeignete, … maximal erreichbare Punktzahl (AFB) EK ZK DK 4 (I) 2 erklärt die Bedingungen … 3 (I) 3 erklärt die Bedingungen … 3 (II) 4 gibt Aussagen an … 3 (II) 5 gibt Aussagen an … 3 (II) Teilaufgabe b) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl (AFB) 1 berechnet den Winkel … 2 (I) 2 gibt den Gangunterschied … 2 (I) 3 stellt eine Beziehung … 3 (II) 4 berechnet mit Hilfe … 4 (I) EK ZK DK Teilaufgabe c) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl (AFB) 1 nennt den hier … 2 (I) 2 berechnet mit Hilfe … 4 (II) 3 nennt die Gleichung … 3 (I) 4 führt die Rechnung … 6 (II) EK ZK DK Teilaufgabe d) Anforderungen Lösungsqualität Der Prüfling maximal erreichbare Punktzahl (AFB) 1 begründet, dass in … 3 (III) 2 erklärt, dass beim … 3 (II) begründet, dass aufgrund … 3 (III) 3 Summe 2. Aufgabe 51 Summe der 1. und 2. Aufgabe 106 Summe insgesamt 106 aus der Punktsumme resultierende Note Note ggf. unter Absenkung um ein bis zwei Notenpunkte gemäß § 13,2 APO-GOSt Paraphe Nur für den Dienstgebrauch! EK ZK DK PH GK HT 1 Ministerium für Schule und Weiterbildung NRW Seite 12 von 12 ggf. arithmetisches Mittel der Punktsummen aus EK und ZK: ___________ Die Klausur wird mit der Note: ___________________________________ (____Punkte) bewertet. Unterschrift, Datum: Grundsätze für die Bewertung (Notenfindung) Für die Zuordnung der Notenstufen zu den Punktzahlen ist folgende Tabelle zu verwenden: Note Punkte Erreichte Punktzahl sehr gut plus 15 106 – 101 sehr gut 14 100 – 96 sehr gut minus 13 95 – 90 gut plus 12 89 – 85 gut 11 84 – 80 gut minus 10 79 – 75 befriedigend plus 9 74 – 69 befriedigend 8 68 – 64 befriedigend minus 7 63 – 59 ausreichend plus 6 58 – 53 ausreichend 5 52 – 48 ausreichend minus 4 47 – 41 mangelhaft plus 3 40 – 35 mangelhaft 2 34 – 28 mangelhaft minus 1 27 – 22 ungenügend 0 21 – 0 Nur für den Dienstgebrauch!