Sternenstehung und Entwicklung - Die Entstehung von Elementen
Werbung

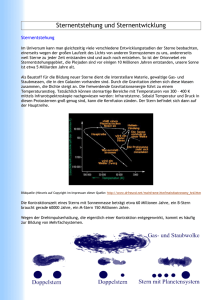
Hauptseminar WS 2005/2006 Astroteilchenphysik und kosmische Strahlung Sternenstehung und Entwicklung Die Entstehung von Elementen bis zum Eisen Inhalt • • • • • • 1 Die Vermessung und Klassifizierung von Sternen 2 Von der interstellaren Gaswolke zum Protostern 3 Der Protostern auf dem Weg zur Hauptreihe 4 Das Hauptreihenstadium 5 Die Entwicklung nach der Hauptreihe 6 Literatur 1 Die Vermessung und Klassifizierung von Sternen • • • • Klassifizierende Messgrößen der Sterne für Sternentwicklungsbeschreibung benötigt Vermessung der momentanen Sternpopulation (Datengewinnung) Dadurch Rückschlüsse auf die durchlaufenen Lebensphasen eines Sterns möglich (Scharmittel =Zeitmittel) Im Folgenden: Beschreibung und Gewinnung wichtiger Messdaten 1.1 Die Bestimmung der Entfernung • Trigonometrisches Verfahren r 1AE 1AE tan Definition der Parallaxensekunde: 1' ' r 206.265 AE 3,0857 1016 m 3,26ly 1 par sec Bei genauer Berechnung: -Erde auf Ellipsenbahn -rel. Position des Sterns zur Ekliptik Bessere Auflösung im Weltall → Satellit HIPPARCOS (1987-1991): 120.000 Sternabstände vermessen 4.000 mit 5% //300 mit 1% Genauigkeit → Nachfolger GAIA (2012-2016) 1' ' 1 206265rad aE 1AE 1,495978 1011 m • Cepheiden-Verfahren Cepheiden (←Sterne) ändern mit Periode P scheinbare Helligkeit m empirisch gefundener Zusammenhang zwischen absoluter Helligkeit M v und P für 2 verschieden Populationen: M V ( PopI ) 1,67 2,54 lg P 1d • MV ( PopII ) 0,27 2,54 lg P 1d →m und P messen und mit Entfernungsmodul m M 5 lg( r 10 pc) Abstand r bestimmen F F ( ) m 2,5 lg F F0 unterscheide visuelle mv, bolometrische mb und M v m(r 10 par sec) spektrale Helligkeit ms ! Hubble-Verfahren (Für weit entfernte Objekte) [ F ] W m2 Energieflussdichte Rotverschiebung des Spektrums→ v mit dem Hubble-Gesetz folgt damit r vr H 0 r 60kms1Mpc 1 H 0 80kms1Mpc 1 1.2 Die Bestimmung des Radius und der Masse • • • • • • Winkeldurchmesser von Sternen zu klein für optische Auflösung Nutzung von Beugungseffekten von Sternenlicht z.B. am Mondrand → Bestimmung des Radius mithilfe der Beugungstheorie Für große Sterne kann man die Stellar-Interferometrie verwenden. → 2 Spiegel, Abstand d +Spektralfilter → Interferenzmuster in Abh. von d → Aus dem Interferenzmuster Bestimmung des Radius An Beteigeuze (Roter Riese) zuerst durchgeführt: →300-facher Sonnenradius! Verbesserung des Verfahrens mit elektronischen Hilfsmitteln Doppelsternsysteme nötig zur Bestimmung der Sternenmasse Doppelsterne sind keine Ausnahme! (>50% sind Teil eines Mehrsternsystems) Um Kepplergesetze anwenden zu können z.B. Visuelle Doppelsterne nötig: Sterne müssen getrennt voneinander beobachtbar sein • zu messende Größen: Umlaufzeit T, Entfernung von S zur Sonne, Massenabstände a1 , a2vom Schwerpunkt S • Schwerpunktsatz→ M1 M 2 a2 a1 große Halbachse in rel. K.: a a1 a2 a1 M 2 M1 M 2 a , a2 M1 M1 M 2 a +3. keplerschen Gesetz → • • 4 2 a 3 M1 M 2 G T2 damit sind M1 & M 2berechenbar Berücksichtigung von Orientierung der Rotationsebene wichtig! Kann mit Keplergesetzen rausgerechnet werden. • Spektroskopische Doppelsterne Abstände zu klein für visuelle Trennung! → Messung der Doppleraufspaltung des Spektrums → Berechnung der Bahngeschwindigkeiten und Umlaufdauer → Aus T und v‘s Berechnung der a‘s → Massen können dann wie bei visuellen Doppelsternen bestimmte werden • • Photometrische Doppelsterne Nur 1 Stern sichtbar, Helligkeit schwankt periodisch → 2 umeinander rotierende Sterne mit gegenseitiger Bedeckung Aus der Helligkeitskurve berechenbar: • Verhältnis der Sternradien R1/2 • Verhältnis der Leuchtkräfte L1/2 Bei bekannten Bahngeschwindigkeiten sogar die Absolutwerte für R1/2 Astronomische Doppelsterne Nur 1 Stern erkennbar, der sich mit unsichtbaren Begleiter um Schwerpunkt dreht. (schwarzes Loch, Neutronenstern, schwarzer Zwerg) • Optische Doppelsterne Kein echtes Doppelsternsystem, da Sterne räumlich voneinander getrennt. →scheinbarer Doppelstern L 4r 2 Fb [ L] W 1.3 Spektraltypen • • • Jeder Stern besitzt charakteristisches Wellenlängenspektrum Absorptionslinien, Emissionslinien und Banden Spektrallinienintensität hängt empfindlich ab von: -Temperatur -chemischen Zusammensetzung der verschiedene absorbierenden und emittierenden Oberflächenschichten Modell: Sternoberfläche = Schwarzkörperstrahler Nach Wienschen-Verschiebungsgesetz: m T const → Je höher die Oberflächentemperatur T, desto weiter wandert das Spektrum in den kurzwelligen Bereich. Grob: „Je heißer die Oberfläche des Stern, um so bläulicher sein Licht“ Kugelsternhaufen M10 • • Aufnahme von 400.000 Spektren am HarvardObservatorium → Harvard-Klassifikation basierend auf der Intensitätsverteilung wichtiger Absorptionslinien z.B.: Balmerserie H-Atom Linien des He-Atoms neutralen Fe Ca-Ion CN-Radikal TiO-Molekül Zuordnung der Sterne zu einer Spektralklasse: ←steigende Oberflächentemperatur • • Später in jeweils 10 Unterklassen verfeinert S und C später hinzugefügt da mehr Verbindungen als in M enthalten • Beispiel für eine HarvardKlassifikationstabelle 1.4 Hertzsprung-Russel-Diagramm • 1910-1913 Enjar Hertzsprung (1873-1976) & Henry Norris Russel (1877-1957): Trägt man absolute Helligkeit über Spektralklasse/Temperatur auf → Hertzsprung-Russel-Diagramm (HRD) → Sterne gruppieren sich in bestimmen Gebieten → Sterne in einer Gruppe haben ähnliche Eigenschaften • • Unterscheidung von Sternen mit gleicher Spektralklasse bei völlig verschiedenen Leuchtkräften nötig! → MKK- /Yerkes-Klassifikation später verfeinert zur MK-Klassifikation: 0 Extrem leuchtkräftige Super-Überriesen Ia Überriesen mit großer Leuchtkraft Ib Überriesen mit geringer Leuchtkraft II Riesen mit großer Leuchtkraft III Normale Riesen IV Unterriesen V Hauptreihensterne (Zwergsterne) VI Unterzwerge • 1952 Sir Arthur Stanley Eddington (1882-1944) Empirische Masse-Leuchtkraftrelation für Sterne der Hauptreihe: L M Für kleine Sternmassen M 0,5M sonne : 4 Für große Sternmassen M 3M sonne : 3 2 Von der interstellaren Gaswolke zum Protostern • • • Sterne Orte hoher Massenkonzentration ↔ mittlerer Dichte im interstellaren Raum →Entstehung durch Akkumulation der Materie wegen Gravitation Gegen Kontraktion wirken: -Kompensation durch Drehimpuls -thermodynamischer Gasdruck interstellare Materie besteht hauptsächlich aus H, He, wenig schwere Elementen → Ideale Gasgleichung p V R T kann verwendet werden Abschätzung, wann eine Wolke kontrahieren kann: Für ein Gasteilchen muss gelten M m 3 E pot G Ekin k BT R 2 • Mit kugelförmiger Wolke & konstanter Massendichte 4 M V n m V V R 3 3 9 k BT 1 81k B3 T3 R MJ 2 3 8 Gm2 n m 32G n Von James Jeans bereits 1926 berechnet → MJ = jeanssche Masse Kriterium ab wann Wolke kollabiert = Jeanskriterium 3 4 T M J 3 10 M Sonne M Sonne 1,989 1030 kg [n] # Atome m3 n Rechenbeispiel: -interstellare Wolke aus neutalem H: n 106 m 3 T 100K M J 30.000 M Sonne -dichte, kalte Dunkelwolke: n 1012 m 3 T 10K M J 1 M Sonne • • • • • • • • • • • →Mehrere Sterne entstehen gleichzeitig aus einer ~10pc großen Wolke mit ein paar 10.000 Sonnenmassen Wolke kontrahiert, Dichte↑ T=const, da Energie nach außen abgestrahlt → Jeansmasse sinkt! → Kondensationskerne bilden sich Wolke fragmentiert (Drehimpuls hilft mit!) bis Dichte in den Fragmente Abstrahlung verhindert → freigesetzte Energie geht in kinetische Energie über →T↑ → MJ↑ →keine weiteren Kondensationskerne Im Innern der Kerne steigt Druck an → Verlangsamung der dortigen Kontraktion Von außen fällt weiterhin Materie fast im freien Fall in den Kern → Aufheizung Ab jetzt: Kondensationskern= Protostern Auslöser solcher „spontaner“ Kontraktionen: Supernovaexplosionen in der Nähe • Grobe Abschätzung der Minimalen Kollapszeit: Wie lange fällt Teilchen bis ins Massezentrum, wenn Gasdruck wegfällt? mM (r ) 4 M ( r ) r 3 Kraft auf Teilchen: F G 2 3 r 4 r(t ) G r 4 r(t 0) 0 3 G 3 r (t ) r0 cos( t ) t fall 1 3 2 4 G Wertebeispiel: n 10 5 H Atome / m 3 1,67 10 19 kg / m 3 • G 6,67 10 11 m3 kg 1 s 2 t fall 2,3 1014 s 7,3 106 a →Kurze Zeit im Vergleich zu anderen Phasen! Abschätzung mit Vorsicht zu genießen! Aber: Wenn Dichte abhängig vom Radius/Zeit → Nichtlinear partielle DGL muss gelöst werden! 3 Der Protostern auf dem Weg zur Hauptreihe • • • • • • • • • Materiewolke hat schon kugelförmige Gestalt kg Ab einer Dichte von 10 7 3 und T 100K kaum noch Energieabstrahlung m aus Wolkeninnern Ab da Wolke=Protostern mit adiabatischem Druckanstieg: TV 1 const pV const Steigender Gasdruck wirkt dem Gravitationsdruck entgegen → Kontraktion langsamer → „1. quasistatische Phase“ Kerndichte und T gehen langsamer ↑ Ab T=1800K Energieverlust durch H2-Dissoziation → T&p ändern sich wenig → Kontraktionsgeschwindigkeit ↑ „2. dynamischer Kollaps“ Hülle heizt sich auf 700K auf → Protostern = Infrarotstern Materie von außen fällt immer noch in de Kern und heizt ihn auf Bei T 10 4 K bis T 10 5 K Ionisation H und He • • • • • • nachdem H und He vollständig ionisiert: Gasdruck=Gravitationsdruck → „hydrostatisches Gleichgewicht“ Radius von 100AE auf 0,2AE weiteres Aufheizen durch Materiezustrom Lichtdurchlässigkeit klein → Energietransport durch Konvektion T ( r ) T (r ) Konvektion effektiv → er klein r r → Kerntemperatur ≈ Oberflächentemp. →Leuchtkraft relativ hoch: L 4R 2 T 4 Protostern taucht im HRD rechts auf. Höhe abhängig von der Masse ↔ Radius • • • • • • • • • • C.Hayashi: Stabilitätsforderung für vollständig konvektive Sterne ergibt Beziehung zwischen L und TOberfläche in Abhängigkeit der Masse Im HRD: Fast senkrechte Hayashi-Linie Alle Protosterne rechts davon instabil → konvergieren mit der Zeit auf die HL Auf der HL folgt langsame Kontraktion → Radius↓ ,T bleibt gleich → L 4R 2 T 4 ↓ Protosterne wandern auf HL nach unten Kerntemperatur steigt weiter an → Strahlungsdurchlässigkeit↑ → Energie wird verstärkt durch Strahlung transportier → Protostern nicht mehr vollständig konvektiv → Verlassen der HL nach links Temperatur im Kern steigt weiter an →Beginn von Kernfusionsprozesse (Teile der pp-Kette schon früh!) Nun „verdrängt“ die Fusionsenergie die Gravitationsenergie Bei Sternen mit großer Masse setzt Fusion früher ein als bei ... kleiner Masse Modellrechnungen: „Kondensation“ zur Hauptreihe stark massenabhängig Stern mit 15-facher Sonnenmasse 60.000a `` 0,1-facher `` hunderte Millionen a • Eintritt in die Hauptreihe durch Start der pp-Fusionskette bei 4 Millionen K festgelegt. 4 Das Hauptreihenstadium • • • • Sterne mit weniger als 0,008 Sonnenmasse erreichen HR nicht T im Kern zu gering → Abstrahlung der Gravitationsenergie → Gravitationsdruck = Gasdruck → „brauner Zwergstern“ Sterne mit mehr als 100 Sonnenmassen erreichen HR nicht T im Kern extrem hoch → Strahlungsdruck T 4 spielt nun wesentliche Rolle → Treibt die Materie nach außen → Protostern instabil Hauptreihensternmassen von 0,008-100 Sonnenmassen 70 Sonnenmassen-Stern schon nachgewiesen 4.1 Die Abhängigkeit der Lebensdauer von Leuchtkraft und Masse • Abschätzung der Verweilzeit im HR-Stadium mit „Eddingtonformel“: 3 4 L M verwende pro H-Atom erzeugte Energie aus pp-Prozess: E H 5MeV 8 10 13 J Vereinfachung: Stern besteht vollständig aus H M EH HR HR M 2 L mH Es können aber nur 10% „verbrannt“ werden da nur Kern genügend Energie: ( 10%) Sonnenwerte einsetzten: mH 1,67 10 27 kg M 20M Sonne 10 9 a M Sonne 2 1030 kg LSonne 3,85 10 26W HR 6 109 M Sonne M Jahre Genauere Modelle: z.B. Berücksichtigung der Konvektion → HR-Brennphase der Sonne 10 Milliarden Jahre (Hälfte der Zeit schon um!) 2 4.2 Energiegewinnung von Hauptreihensternen in Abhängigkeit der Masse • • Energiegewinnung auf HR definitionsgemäß Fusion von H Jedoch Unterschiede in Abhängig von der Masse 0,08-0,25 Sonnenmasse: Nur in kleinem Zentralgebiet Zündtemperatur für pp-Kette erreicht → großer Temperaturgradient → vollständig konvektiv (gesamter H-Vorrat wird verbraucht!) 0,25-1,5 Sonnenmasse: Energieerzeugung durch pp-Kette in ausgedehntem Bereich r 0,3R → Temperaturgradient im Innern klein → Energietransport dort durch Strahlung Weiter außen Zunahme der Strahlungsabsorption (wegen geringem T) →Konvektion übernimmt Energietransport → Zentrum radiativ, Hülle konvektiv • Sterne mit mehr als 1,5-facher Sonnenmasse CNO-Zyklus (große T-Abhängigkeit) hier wichtig Verantwortlich für Energieproduktion in kleinem Kerngebiet →Energieflussdichte dort sehr hoch →Temperaturgradient im Kern hoch →Konvektion übernimmt dort Energietransport →dort gute Durchmischung der Materie Weiter außen pp-Kette dominant In der Hülle keine Kernreaktion → Temperaturgradient dort sehr klein → Energietransport durch Strahlung → Zentrum konvektiv, Hülle radiativ 5 Die Entwicklung nach der Hauptreihe • Die Entwicklung nach der Hauptreihe sehr massenabhängig → Verlaufsbeschreibung in Abh. der Masse 5.1 Sterne mit 0,08-0,26-facher Sonnenmasse • • • • Sterne waren in Brennphase vollständig konvektiv → H-Vorrat vollständig verbraucht →bestehen überwiegend aus Helium Zündtemperatur von He-Brennen wird nicht erreicht →Kontraktion des Sterns bis Gravitationsdruck = Entartungsdruck der Elektronen Nach Durchlauf einer instabilen Phase → „weißer Zwerg“ Nach Abstrahlung der verbleibender Energie → „schwarzer Zwerg“ 5.2 Sterne mit 0,26-3-facher Sonnenmasse • Nachdem H-Vorrat im Kern aufgebraucht → Kontraktion des Kerns →Potentielle Energie wird thermische Energie →Aufheizung der Schale bis zur Zündtemperatur →H-Schalenbrennen →Expansion zum Roten Riesen Für Sterne mit mehr als 0,5 Sonnenmassen T im Kern erreicht 108 K → He-Brennen = 3-α-Prozess (He→C): • He 4He 8 Be 8 Be 4He 12 C E 0,1MeV E 7,4MeV 4 8 Be instabil: 2,5 1016 s → Beide Reaktionen müssen fast gleichzeitig ablaufen → 3 α-Teilchen müssen fast gleichzeitig zusammentreffen • Wegen ihrer Seltenheit tragen folgenden Alphareaktionen im He-Brennstadium kaum zur Energieerzeugung bei sind aber möglich: 12 C 4He 16 O , 16 O 4He 20 Ne , Ne 4He 24 Mg . für Sterne mit weniger als 1,4 Sonnenmassen (und mehr als 0,5): He-Kern vor He-Zündung enthält entartete Elektronen → neben Gasdruck der Ionen viel größere Entartungsdruck des Elektronengases kompensiert Gravitationsdruck → zum Zeitpunkt der He-Zündung keine Expansion des Kernvolumens nur T↑, aufgrund der Eigenart des entarteten Elektronengases → beschleunigte Reaktionsrate bei Fusionsprozessen Erst wenn Gasdruck > Entartungsdruck hebt sich Entartung auf → Stern nicht mehr im Gleichgewicht → Strahlung und gewaltige Druckwelle wird von Hülle absorbiert →Leuchtkraft des Sterns steigt für ~ 100s auf das 10 4 10 6-fache →He-Flash 20 • • für Sterne mit mehr als 1,4 Sonnenmassen: He-Fusion läuft kontinuierlich an, da • H-Brennphase: konvektives Innere • früher hohe Kerntemperaturen → Kernmaterie noch nicht entartet (kein Entartungsdruck durch e-) • Danach wandert Stern durch mehrer Instabile Phasen (Oszi. Im HRD) zum Ast der roten Riesen • Radius solcher Riesensterne bis 250-fachem Sonnenradius • Heliumvorrat im Kern aufgebraucht → He beginnt in der H-Brennschale zu brennen → H-Brennschale wandert nach außen → 2 Schalen expandieren, Kern kontrahiert → Kern stößt größere Teile der Hülle ab → planetarischer Nebel → Überreste des Kerns → weißer Zwerg →schwarzer Zwerg wenn M von Rest < Chandrasekhargrenzmasse M C 1,5M Sonne Gleichgewichtsbedingung nach Subrahamanyan Chandrasekhar (1920-1994) für Sterne mit: Entartungsdruck e- = Gravitationsdruck Für die Radien gilt: RC 10 4 km Mit M C ergibt sich: R M 1 3 5.3 Sterne mit mehr als 3-facher Sonnenmasse • • • • H-Brennen ähnlich wie bei 1,4-3-facher Sonnenmasse Kein He-Flash He-Vorrat im Kern aufgebraucht → Kern kontrahiert → He-Schalenbrennen → T im Kern ↑ → die seltenen α-Reaktionen gewinnen an Bedeutung →neue Reaktionen kommen hinzu →Sternradius wächst nochmals → Überriese C-Brennen ab 5 10 8 K 12 C 12C 24 Mg E 13,93MeV 23Mg n E 2,61MeV 23Na p E 2,24MeV 20 Ne 4He E 4,62MeV 16 O 2 4 He E 0,114MeV • • Brennprozesse nach ca. 100 Jahren im Kern beendet →Verlagerung in die He-Brennschale Ne-Brennen für mehr als 13 Sonnenmassen ab T 1,5 10 9 K T so hoch, dass Photodissoziation der Ne-Kerne einsetzt Photodissoziationsre aktion : 20Ne 16 O 4He O 4He 20 Ne, 16 Fo lg ereaktion : Ne 4He 24 Mg , 20 Mg 4He 28Si . 24 • Brenndauer: ca. 1 Jahr O-Brennen für Sterne mit genügend Masse ab 2 10 9 K 16 O 16O 32 S E 16,54MeV 31S n E 1,46MeV 31P p E 7,68MeV 24 g 2 4 He E 0393MeV 28Si 4He E 9,59MeV Brenndauer: einige Monate • Letzte energieerzeugende Brennstufe: Si-Brennen bei T 4 109 K 28 Si 28Si 56 Ni 56 Ni 56 Co e Co 56 Fe e Brenndauer: etwa einen Tag Durch freigesetzten Photonen Entestehung andere Elemente durch Photodissoziation möglich: 56 • • • 28 Si 27 Al p E 11,58MeV 28 Si 24Mg 4He E 9,98MeV Aufbau des Sterns im Si-Brennstadium nach dem Zwiebelschalenmodell Si-Vorrat aufgebraucht →alle Energiequellen erschöpft →Kollaps im fast freien Fall →Hüllenmaterie prallt mit hoher Geschwindigkeit auf hochverdichteten Kern aus Neutronen. Dabei wird sie in den Raum zurückgeschleudert →Supernova Typ II • • • • Leichtere Sterne erreichen Si-Brennstufe nicht Werden bei einem Carbon*- oder Oxygenflash* zerrissen * laufen analog wie He-Flash sind aber gewaltiger! → Explosion: Supernova Typ II Verbleibende Stern: Neutronenstern** Solange 3,2M Sonne M OV M M C 1,5M Sonne **bestehen aus entartetem Neutronengas mit Dicht von Kernmaterie →Bei 2-4-Facher Sonnenmasse Radius ≈10km ! ANMERKUNG: Alle Entwicklungsverläufe nach der HR basieren auf theoretischen Überlegungen und Modellen die noch auf unvollständig bekannten Faktoren beruhen! → z.B. angegebene Massenzahlen variable! 6 Literatur [1] W. Demtröder: Experimentalphysik 4 Kerne-, Teilchen- und Astrophysik; SpringerVerlag. [2] H.Karttunen et. al: Fundamental Astronomy; Springer Verlag. [3] Reinhardt Lermer: Grundkurs Astronomie; Bayrischer Schulbuch-Verlag. [4] Trinh, Xuan-Thuan: Die Geburt des Universums; Verlag Otto Maier Ravensburg. [5] Simon Goodwin: Mission Hubble, Das neue Bild des Universums; Bechtermünz Verlag. [6] Joachim Herrmann: Welcher Stern ist das?; Franckh-Kosmos-Verlag [7] Internet.