Einführung in die nichtlineare Dynamik

Einführung in die nichtlineare Dynamik
Stefanie Russ
15. April 2009
1
Nichtlineare Dynamik und deterministisches Chaos
Die klassische Mechanik beschreibt (wie übrigens auch die Quantenmechanik) deterministische Physik. Daher nahm man lange Zeit an, dass sich die Bewegung (Dynamik) eines beliebigen klassischen Systems bei
genauer Kenntnis der Anfangsbedingungen für beliebig lange Zeit prinzipiell vorausberechnen lässt. Die
notwenige Technik dafür haben Sie in den Mechanikvorlesungen des Grundstudiums gelernt: mit Hilfe der
dynamischen Grundgleichung oder des Lagrange- oder Hamiltonformalismus sucht man die Bewegungsgleichungen und löst die so gefundenen Differenzialgleichungen unter den gegebenen Anfangsbedingungen. Bei
komplizierten (eventuell gekoppelten) Bewegungsgleichungen mag die Lösung mathematisch anspruchsvoll
sein, eventuell mögen die passenden Rechentechniken fehlen. Im schlimmsten Fall jedoch lassen sich die
Lösungen dann mit Hilfe des Computers durch numerische Integration bestimmen. An dieser Vorstellung
ist zunächst einmal nichts Falsches.
Indirekt nahm man jedoch zusätzlich an, dass Bewegungen, die sich durch so klare mathematische Gesetzmäßigkeiten wie Differenzial- oder Differenzengleichungen beschreiben lassen, ”geordnet” verlaufen und
nicht nur prinzipiell, sondern auch ganz praktisch vorhersagbar sein müssten. Dies ist jedoch normalerweise nicht der Fall, sondern nur dann, wenn das betrachtete System sich nicht chaotisch verhält. Ein erster
Hinweis auf chaotisches Verhalten findet sich bereits im 19. Jahrhundert bei Poincaré für das Dreikörperproblem, der zweite bei Lorenz 1963 für einfache Modellgleichungen aus der Wettervorhersage. Um anzudeuten,
dass sich dieses chaotische Verhalten aus durchaus deterministischen Gleichungen entwickelt und dass jeder
momentane Zustand des Systems sehr wohl deterministisch aus dem vorhergehenden Zustand folgt, wurde
der Begriff ”deterministisches Chaos” geprägt. Inzwischen ist klar, dass chaotisches Verhalten in Physik
und Natur nicht die Ausnahme, sondern die Regel ist. Es tritt nur bei nichtlinearen Bewegungsgleichungen
auf. Ein häufiger Grund für nichtlineare Terme in den Bewegungsgleichungen sind Rückkopplungseffekte.
Die Definition, was genau mit dem Begriff ”chaotisches Verhalten” gemeint ist, wirkt oft etwas verschwommen. Dies mag daran liegen, dass chaotisches Verhalten nach und nach an vielen Beispielen entdeckt
wurde und sich die Gemeinsamkeiten aller Beispiele erst langsam herauskristallisierten. Die erste (sehr
anschauliche) Definition beschreibt die Sensitivität des dynamischen Verhaltens eines Systems zu seinen
Anfangsbedingungen. Dies wird durch folgende (miteinander verwandte) Kriterien beschrieben.
• Die Koordinaten eines chaotischen Systems hängen so stark von den Anfangsbedingungen ab, dass
kleinste Abweichungen sich innerhalb kürzester Zeit zu großen Fehlern aufschaukeln. Sinnvolle Vorausberechnungen der Trajektorien sind daher nicht möglich.
• Trajektorien, die mit leicht unterschiedlichen Anfangsbedingungen starten, entfernen sich in Systemen
mit chaotischer Dynamik exponentiell voneinander (Schmetterlingseffekt), anstatt nur linear, wie es
in regulären Systemen der Fall ist.
• Beobachtet man ein Experiment mit chaotischer Dynamik (Beispiel: Dreikörperstreuung, Doppelpendel), so erhält man den Eindruck, dass der Ausgang des Experimentes zufällig erfolgt.
Dieses Verhalten wird durch den Lyapunov-Exponenten ausgedrückt. Wenn sich eine Koordinate ξ(t) einer
Trajektorie exponentiell von ihrem Anfangswert ξ0 entfernt, so lässt sie sich (für große t) beschreiben durch
|ξ(t)| = |ξ0 | exp[λt]
(1)
mit dem numerisch und experimentell oft recht gut zu bestimmenden Exponenten λ (Lyapunov-Exponent),
1 ξ(t) .
(2)
λ = lim ln t→∞ t
ξ0 1
Verläuft die Trajektorie nicht chaotisch, so erkennt man dies an einem Lyapunov-Exponenten λ ≤ 0.
(Nachteil: Um den Lyapunov-Exponenten zu bestimmen, muss man laut Definition zu unendlich großen
Zeiten, im praktischen Fall aber mindestens zu sehr großen Zeiten gehen, was nicht immer praktikabel ist.)
Diese Beschreibung ist allerdings etwas ungenau und vernachlässigt die Möglichkeit, dass Bahnen sich auch
zufällig wieder einander nähern können (und sogar sollen), so dass mit dem Abstand δ eher die Unschärfe
als ein wirklicher Abstand gemeint ist. Um dies auszudrücken ist die ”Lyapunov-Zeit” TLyap in Gebrauch.
Sie ist die Zeit, in der der mittlere Abstand δ zweier (i.A. zu Beginn benachbarter) Bahnen, von δ0 auf die
Systemgröße L angewachsen ist.
1 δ0 1 L (3)
TLyap ∼ − ln = ln .
λ
L
λ
δ0
Nach Ablauf dieser Zeit wirkt der Wert der Koordinate ξ zufällig, d.h. er befindet sich scheinbar unabhängig
von seinem Startpunkt ”irgendwo” im System, auch wenn der Abstand zwischen den Bahnen dann natürlich
nicht mehr weiter anwächst.
Indirekt haben wir bei dieser Beschreibung von Chaos somit vorausgesetzt, dass sich die verschiedenen
Trajektorien (im Ortsraum, nicht Phasenraum) auch wieder treffen, sich die Bewegung also in einem begrenzten Gebiet abspielt. Wenn sich Trajektorien nur exponentiell voneinander entfernen, so wertet man
dies i.A, noch nicht als chaotisches Verhalten. Als zusätzliche Bedingung müssen sich die Trajektorien
auch wieder treffen und sich ununterscheidbar miteinander vermischen. Erst dies macht die Berechnung
chaotischer Trajektorien so schwierig.
Diese Eigenschaft nennt man die ”Mischeigenschaft” oder auch ”Mixing”. Sie wird formal beschrieben,
indem man den Raum, in dem die betrachtete Bewegung abläuft in verschiedene Gebiete aufteilt, und
feststellt, ob und inwieweit Trajektorien, die in einem Gebiet starten, im Laufe der Bewegung auch andere
Gebiete erreichen. In einfachen Systemen, wie z.B. in Billardsystemen oder im Dreikörperstreuproblem ist
dies mit der Anzahl der Reflexionspunkte einer Trajektorie verknüpft. Je mehr verschiedene Reflexionspunkte, umso stärker vermischen sich die Trajektorien. Daher wird die Mischeigenschaft über die Anzahl
N der verschiedenen Trajektorien mit n Reflexionspunkten gemessen. Von Mischeigenschaft spricht man
(in diesen Systemen), wenn auch hier ein Exponentialgesetz gilt,
N (n) ∼ exp[hn],
(4)
wobei die ”topologische Entropie” h die Zunahme der Trajektorien mit n beschreibt.
Die Eigenschaften (1) und (4) zusammen mit positivem λ und h werden als chaotisches Verhalten bezeichnet. Auch andere Bezeichnungen sind in Gebrauch, wie z.B. der Begriff der Turbulenz oder auch
verschiedene ”Wege ins Chaos”, von denen die Periodenverdopplung der am leichtesten verständliche ist.
”Intermittenz” dagegen beschreibt als weiteren Weg ins Chaos, wie ein in weiten Teilen periodisches Signal
beim Anwachsen eines Kontrollparameters durch Intervalle ungeordneter Bewegung unterbrochen wird.
Wichtig ist, dass diese Eigenschaften und ”Wege ins Chaos” universell sind, d.h. in chaotischen Systemen
vieler völlig verschiedener physikalischer Probleme auftauchen.
2
2.1
Definitionen und Klassifizierungen
Nichtlineare Systeme, Dynamische Systeme und diskrete Abbildungen
Nichtlineare Systeme: Nichtlineare Systeme sind dynamische (physikalische) Systeme, wie z.B. Doppelpendel, Kettenkarussell, etc., die durch nichtlineare Bewegungsgleichungen beschrieben werden. Diese
Bewegungsgleichungen ergeben sich direkt aus der Physik.
Dynamische Systeme: Mit dynamischen Systemen bezeichnet man einfache Modellsysteme (bekanntestes Beispiel: Lorenz-Gleichungen zur Konvektion), die komplexere physikalische Probleme auf einfachere
Art beschreiben sollen. Wann immer man Computersimulationen ausführt, wird man zuerst das gegebene
physikalische Problem auf ein einfacheres System reduzieren müssen, welches allerdings die wesentlichen
Züge des gegebenen Problems noch enthält. Auch für dynamische Systeme (Modellsysteme) wird man i.A.
nichtlineare Differenzialgleichungen wählen (zumeist gekoppelt). Beispiel Lorenz-Gleichungen:
ẋ =
ẏ =
s(y − x)
rx − y − xz
ż
xy − bz,
=
2
(5)
mit den Parametern s, r und b und den Variablen x(t), y(t), z(t). Dynamische Systeme können zeitlich
kontinuierlich oder diskret sein.
Diskrete Abbildungen: Diskrete Abbildungen folgen aus Differenzengleichungen oder aus Iterationsvorschriften
xn+1 = f (xn ).
(6)
Bekanntestes Beispiel: Logistische Gleichung xn+1 = rxn (1 − xn ). Interessanterweise lässt sich schon hier
der Weg ins Chaos anhand der Periodenverdopplung verstehen (”Feigenbaum-Diagramm”).
2.2
Stochastische Prozesse
Stochastische Prozesse werden durch Differenzialgleichungen beschrieben, die Zufallsterme enthalten, d.h.
Terme, bei denen z.B. Übergangswahrscheinlichkeiten vorkommen, oder die auf andere Art Zufallszahlen ri
erfordern. Die Existenz von Zufallsvariablen alleine (”Rauschen”) kann auch ohne nichtlineare Terme einen
Übergang zu chaotischem Verhalten erwirken. Von daher werden stochastische Gleichungen auch eingesetzt,
um nichtlineare Prozesse (einfach) zu beschreiben. Typische Probleme aus dem Bereich der stochastischen
Gleichungen beschreiben z.B. Clusterwachstum oder den Random Walk, etc. Einige stochastische Gleichungen lassen sich analytisch lösen, wenn man die Verteilungsfunktion P (ri ) der verwendeten Zufallszahlen
kennt. Man sucht in diesen Fällen meist nach der Wahrscheinlichkeitsverteilung P (x, t) einer bestimmten
Koordinate, z.B. nach der Wahrscheinlichkeit, dass sich ein Random Walker zur Zeit t am Ort x aufhält.
Die speziellen Trajektorien x(t) dagegen können von Zufallsexperiment zu Zufallsexperiment sehr unterschiedlich sein und schnell auseinanderlaufen und so schon zu chaotischem Verhalten führen. Diese Effekte
werden noch stärker, wenn bereits die Übergangswahrscheinlichkeiten in nichtlinearer Weise von den berechneten Grössen abhängen (wenn beispielsweise beim Clusterwachstum oder bei Geburt-/Sterbeprozessen
von Populationen die Wahrscheinlichkeit dieser Prozesse von der Populationsgrösse abhängt).
2.3
Der Phasenraum
Wenn wir bisher von den Koordinaten eines Systems gesprochen haben, so haben wir damit die (generalisierten) Ortskoordinaten gemeint. Die (kontinuierliche) Änderung der Ortskoordinaten beschreibt die
Bahnkurve oder Trajektorie im realen Raum. Häufiger wird allerdings eine Bewegung durch ihre Trajektorie
im Phasenraum beschrieben, bei dem zu jeder Ortskoordinate qi noch eine Impulskoordinate pi = ∂L/∂ q̇i
hinzukommt. Anders als im realen Raum, können sich chaotische Trajektorien im Phasenraum nicht treffen. Bei einem Schnittpunkt würden sowohl die Orts- als auch die Impulskoordinaten übereinstimmen, so
dass sich die Bewegung von da an exakt wiederholen würde (periodischer Orbit). Es ist wichtig zu wissen,
dass alle Systeme mit Energieerhaltung (konservative Systeme) – auch wenn sie chaotisch sind – immer
auch periodische Bahnen besitzen. Diese spielen eine tragende Rolle beim Vergleich von klassischen mit
quantenmechanischen Systemen (Quantenchaos).
2.4
Konservative und dissipative Systeme
Konservative und dissipative Systeme unterscheiden sich hinsichtlich des zeitlichen Verhaltens ihrer Dichte im Phasenraum, bzw. ihrer Volumenelemente. Dazu müssen wir uns viele verschiedene Trajektorien
im Phasenraum vorstellen. Außerdem definieren wir (willkürlich) kleine Volumenelemente ∆~q∆~
p im Phasenraum, die eine bestimmte Anzahl von Punkten enthalten. Die Phasenraumdichte ist definiert durch
die Anzahl der Punkte im Phasenraumelement. Wenn sich das System zeitlich entwickelt, so können die
Punkte auseinander- oder zusammenlaufen und damit die Größe der Volumenelemente verändern. Ist dies
der Fall, so spricht man von einem dissipativen System. Ein bekannter Grund dafür ist Energieverlust.
Bleiben dagegen die Phasenraumvolumina gleich (und verändern nur ihre Form), so haben wir ein konservatives System vorliegen. Im Phasenraum (q, p) (nur den haben wir hier eingeführt), nennt man diese auch
”Hamilton-Systeme”.
2.4.1
Konservative Systeme in der Quantenmechanik
Bei den konservativen Systemen unterscheidet man klassische und quantenmechanische Systeme und vergleicht i.A. Systeme gleicher Geometrie (Keplerproblem und Bohr’sches Atommodell, klassisches Billard
und quantenmechanischer Potenzialtopf). Hierbei gibt es zwei verschiedene Fragestellungen.
3
• Hilft uns die Lösung des klassischen Problems (Kenntnis der Trajektorie) bei der Lösung des zugehörigen quantenmechanischen Problems?
• Welche Spuren hinterlässt die klassische Dynamik im quantenmechanischen Verhalten eines Systems?
Man stellt fest, dass quantenmechanische Systeme, je nachdem, ob ihre klassische Dynamik regulär
oder chaotisch ist, zwei unterschiedliche Universalitätsklassen bilden. Dies schlägt sich z.B. nieder in
der Statistik ihrer Eigenwerte, aber auch im Aussehen ihrer Wellenfunktionen, deren Knotenlinien
und Maxima (die bei einigen Funktionen als ”Narben” um die klassischen Bahnen herum liegen).
2.5
Attraktoren
Attraktoren sind Punktmengen im Phasenraum, denen sich alle Trajektorien im Einzugsgebiet annähern.
Daraus ergibt sich, dass die Dichte der Punkte in der Nähe der Attraktoren steigt, die Volumenelemente
also kleiner werden. Folglich besitzen nur dissipative Systeme Attraktoren. Als Attraktoren sind bekannt:
Fixpunkte (gedämpftes Pendel), Grenzzyklen und ”seltsame” Attraktoren (strange attractors). Seltsame
Attraktoren kommen in Gebieten mit chaotischen Trajektorien vor. Da sich chaotische Trajektorien im
Phasenraum nicht schneiden, müssen ihre Attraktoren immer neue Strukturen auf immer kleinerem Raum
beherbergen. Diese Attraktoren sind selbstähnlich (fraktal). Es gibt Bahnen, die jedem Punkt eines seltsamen Attraktors beliebig nahe kommen, so dass sich der Attraktor nicht aufteilen lässt. Dies hängt mit der
Mischeigenschaft zusammen. Obwohl Attraktoren im Phasenraum definiert sind, werden sie (aus naheliegenden Gründen) oft im Ortsraum gezeigt. Eine andere Darstellung ist die des Poincaréschnitts
2.6
Poincaréschnitte
Ein Phasenraum hat meistens zu viele Dimensionen, um ihn sich bequem vorstellen zu können. Um die
Bewegung auf ein Objekt kleinerer Dimension abzubilden, bestimmt man gerne die Schnittpunkte der Trajektorie (im Phasenraum) mit einer vorgegebenen (Hyper-)fläche. Damit lassen sich oft sowohl Bewegungen
als auch Attraktoren recht gut bestimmen. Insbesondere die fraktalen Eigenschaften seltsamer Attraktoren
lassen sich sehr schön in Poincaréschnitten sehen.
3
Quantenmechanik und klassische Bahnen: ”Quantenchaos”
Im Folgenden reden wir ausschließlich von Systemen mit Energieerhaltung (konservative Systeme). Aus den
Hamilton’schen Bewegungsgleichungen wissen wir, dass diese Systeme nicht explizit von der Zeit abhängig
sind. Die Beispiele aus der Mechanik sind zahlreich, als besonders bekannt heben wir hier das Keplerproblem
hervor. Die Ähnlichkeit des Keplerpotenzials mit dem Coulomb-Potenzial gab vermutlich die Idee zum
Bohr’schen Atommodell, d.h. zur Idee, die erlaubten Energiewerte En des Wasserstoffatoms zu finden,
indem man nur diejenigen Bahnen zulässt, bei denen der Bahnumfang ein ganzzahliges Vielfaches der
De-Broglie-Wellenlänge ist.
Dies wirft sofort die Frage auf, ob hier eine allgemeine Regel abgeleitet werden kann, ob also die Quantisierungsregeln des Wasserstoffatoms auch für andere Atome oder sogar Moleküle gelten. Diese Frage war
zu Beginn des 20. Jahrhunderts hochaktuell, besonders in den Jahren vor Aufstellung der SchrödingerGleichung (als man also noch keine andere Möglichkeit hatte, die erlaubten Energiewerte zu finden). Die
richtige Idee kam von Einstein, allerdings glaubte er damals, dass diese Art von Lösungen nur für integrable Systeme (siehe unten) möglich seien. Nachdem dann allerdings die Schrödingergleichung eine einfachere
Möglichkeit zur Berechnung der Energiewerte für Teilchen in beliebigen Potenzialen lieferte, geriet Einsteins Arbeit völlig in Vergessenheit. Erst als in den 70er Jahren mit der Gutzwiller’schen Spurformel eine
Möglichkeit gefunden wurde, auch die Energiewerte (genauer gesagt: die Zustandsdichte) ”chaotischer Systeme” (d.h. von Systemen, deren klassische Dynamik sich chaotisch verhält) zu finden, wurde dieses Gebiet
der Physik populär und Einsteins Arbeit wiederentdeckt.
3.1
Integrable Systeme
Systeme, welche so viele Erhaltungsgrößen wie Freiheitsgrade besitzen – eine davon die Energie – (und
außerdem gewisse Stetigkeitsbedingungen erfüllen) nennt man ”integrable Systeme”. Sie kennen aus der
4
klassischen Mechanik die Hamilton-Bewegungsgleichungen:
q̇i =
∂H
,
∂pi
ṗi = −
∂H
,
∂qi
∂H
∂L
=−
,
∂t
∂t
(7)
die für jede unabhängige Koordinate qi gelten. Integrable n-dimensionale Systeme besitzen also n Sätze
von Hamilton-Gleichungen. Meistens separieren die Gleichungen allerdings nicht, sondern jedes pi kann von
allen Koordinaten qi , i ∈ {1, n} und ihren Ableitungen abhängen. Bekanntestes Beispiel ist die Drehimpulskomponente Lz (in Zylinderkoordinaten) Lz = mr2 ϕ̇. Die Bewegungsgleichungen werden viel einfacher,
wenn zyklische Koordinaten auftreten.
Zyklische Koordinate: Dies sind Koordinaten q, von denen die Hamilton- (oder Lagrange-)Funktion
nicht abhängt: H(q, p) = H(p), ∂H/∂q = 0. Dies zeigt eine (eventuell versteckten) Symmetrie des Systems.
Theorem von Noether: Zu jeder Symmetrie gehört ein Erhaltungssatz. Beispiele:
• Wenn das Potenzial V symmetrisch zur z-Achse ist, so hängt V und damit auch H nicht vom Winkel
ϕ ab (Zylindersymmetrie). Daraus folgt die Erhaltung der Drehimpulskomponente Lz .
• Ist das Potenzial sogar punktsymmetrisch zum Ursprung (Keplerproblem), so folgt die Erhaltung
~
aller Drehimpulskomponenten, also die Erhaltung des Gesamtdrehimpulses L.
• Die Beispiele lassen sich beliebig fortsetzen, allerdings sind die verwendeten Koordinaten nicht immer
so anschaulich. Ganze Zweige der analytischen Mechanik befassen sich damit, zyklische Koordinaten
für ein gegebenes Problem zu finden und sogar Transformationen zu finden, die alle Koordinaten
zyklisch werden lassen (Hamilton-Jacobi-Theorie). (Dies kann natürlich nur dann gelingen, wenn das
Problem genügend Erhaltungsgrössen besitzt.)
Betrachten wir nun ganz allgemein einen H-Operator eines konservativen Systems, der mindestens eine
zyklische Variable besitzt. In Anlehnung an obige (anschauliche) Beispiele, nennt man die zyklischen Variablen gerne ”Winkelvariablen” ϕ, ∂H/∂ϕ = 0. Den zugehörigen generalisierten Impuls bezeichnen wir als
J. Im eindimensionalen Fall hängt H dann nur noch von J ab, H ≡ H(J) mit J ≡ ∂L/∂ ϕ̇. Aus (7) folgt:
∂H
J˙ = −
= 0,
∂ϕ
und damit J = konst.
Ebenfalls aus (7) und mit der Zusatzbedingung J = konst folgt
ϕ̇(t) =
∂H
= konst ≡ ω.
∂J
Diese Gleichungen lassen sich integrieren, d.h. wir erhalten die Lösung ϕ(t) der Bewegung auf einfache Art.
J = konst.,
ϕ(t) = ωt + ϕ0 .
Wenn ϕ ein echter Winkel ist, so verläuft die Bewegung im Phasenraum auf einer Ellipse (bei passender
Wahl der Einheiten auf einem Kreis, d.h. einem 1-dimensionalen Torus).
Besitzt das System n Freiheitsgrade (und n Erhaltungsgrößen), so muss man n zyklische Koordinaten
finden, so dass H nur noch von den zugehörigen (konstanten) Impulsen abhängt, H ≡ H(J1 , J2 , . . . , Jn ).
In diesem Fall erhält man für jeden Freiheitsgrad ein integrables Gleichungssystem mit den unabhängigen
Lösungen ϕi (t) = ωi t + ϕi,0 mit verschiedenen aber konstanten Werten ωi . Daher der Name ”Integrable
Systeme”.
Bei zusätzlichen Stetigkeitsbedingungen für die Erhaltungsgrößen verläuft in diesem Fall die Bewegung im
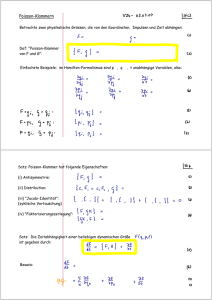
Phasenraum auf einem n-dimensionalen Torus. Dies lässt sich aus der analytischen Mechanik (PoissonKlammern) in Verbindung mit topologischen Überlegungen folgern.
Ein n-dimensionaler Torus besitzt n Möglichkeiten zu Familien periodischer Bahnen (verschiedener Länge),
die man für n = 2 noch gut visualisieren kann. Die allgemeine Bewegung besteht aus einer Überlagerung
aller möglichen Bahnen, wobei die verschiedenen Frequenzen ωi zählen, wie oft jede Klasse periodischer
Bahnen durchlaufen wird. Die allgemeine Bewegung muss nicht periodisch verlaufen (dies hängt davon ab,
ob die verschiedenen ωi in rationalem oder irrationalem Zahlenverhältnis zueinander stehen.)
5
Abbildung 1: Zweidimensionaler Torus
Entlang dieser periodischen Bahnen am Torus lassen sich integrable Systeme quantisieren, d.h. man kann
die erlaubten Energiewerte ähnlich wie im Bohr’schen Atommodell finden. Zu der bekannten Bedingung,
dass die Bahnlänge ein ganzzahliges Vielfaches der De-Broglie-Wellenlänge λ = h/p = 2π/k sein muss,
I
h
2rπ = nλ = n ,
oder
p dx = nh = 2πnh̄
(8)
p
kommt allerdings im allgemeinen Fall noch der ”Maslov-Index” ν hinzu:
I
ν
p dx = nh + h
4
(9)
Dies läßt sich verstehen mit Hilfe der WKB-Methode. Allerdings sind integrable Systeme sehr selten. Ein
einfaches Beispiel, dessen Energiewerte sich auch mit Hilfe der periodischen Bahnen im Phasenraum finden
lassen, ist der harmonische Oszillator.
3.1.1
KAM-Theorem
Werden integrable Systeme (durch zusätzliche Potenziale) gestört, so werden sie durch Verlust von Erhaltungsgrössen normalerweise chaotisch. Wenn allerdings die Störungen nur klein sind, dann werden nicht
alle regulären Bahnen der Tori sofort aufgelöst, sondern einige Bahnen sind schneller, andere langsamer
von den Störungen betroffen. Durch eine Störungsentwicklung konnten Kramer, Arnold und Moser im recht
berühmten ”KAM-Theorem” zeigen, dass Bahnen mit ”möglichst irrationalem” Verhältnis der Torusfrequenzen am längsten stabil gegenüber der Störung bleiben. (Bei sehr starker Störung werden natürlich
irgendwann alle Bahnen instabil.)
Ein sehr populäres Beispiel betrifft die Lücken im Asteroidengürtel (zwischen Mars und Jupiter). Dort gibt
es für bestimmte Umlauffrequenzen ωA keine Asteroiden. Diese würden mit der Umlauffrequenz ωJ des
Jupiter in einem rationalen Verhältnis stehen (Kirkwood 1866):
r
ωA
= .
ωJ
s
Dies lässt sich tatsächlich mit Hilfe des KAM-Theorems erklären: Bei einem System Sonne - Jupiter Asteroid handelt es sich um ein (chaotisches) Vielkörperproblem, das sich aber näherungsweise (unter Vernachlässigung z.B. aller anderen Planeten sowie der Wechselwirkung zwischen den Asteroiden) als Störung
eines integrablen Systems H0 auffassen läßt:
Ungestörter H-Operator: H0 =
p2J
p2
γMS MJ
γMS MA
+ A −
−
2mJ
2mA
rJ
rA
(10)
(Effektives Zweikörperproblem mit ruhender Sonne im Zentrum, Gravitationskonstante γ). Die Wechselwirkung zwischen Asteroid und Jupiter entspricht dann einem zusätzlichen Störterm VJA . (Beachten Sie,
dass Dreikörperprobleme bereits chaotisch sind.)
Wenn wir mit den konstanten Frequenzen ωJ und ωA die periodischen Lösungen von H0 beschreiben, so
finden wir gerade bei den Bahnen, welche rationalen Verhältnissen ωJ /ωA = 1/2, 1/3, 2/5 . . . entsprächen
deutliche Lücken im Asteroidengürtel (Kirkwood Gaps). Daher ist es naheliegend anzunehmen, dass Asteroiden, die sich ursprünglich gerade auf diesen Bahnen befunden haben, durch das Jupiterpotenzial VJA
am stärksten gestört und somit am schnellsten instabil geworden sind.
6
3.2
Quantenbillards
Bei Rechteckbillards (integrable Systeme) lässt sich der 2-dimensionale Torus sogar geometrisch konstruieren und die verschiedenen Orbit(-familien), d.h. deren Länge und Winkel aus vergleichsweise einfachen
grafischen Überlegungen berechnen.
Chaotische Systeme dagegen besitzen weniger Erhaltungsgrößen als Freiheitsgrade. (Bei konservativen
quantenmechanischen Systemen führen die Erhaltungsgrößen – da deren Operatoren mit dem HamiltonOperator vertauschen und nicht explizit von der Zeit abhängen – zu Quantenzahlen.) Die Bewegung von
chaotischen Systemen verläuft daher auf keinem Torus und auf keiner n-dimensionalen Fläche im Phasenraum. Im Extremfall ist bei einem konservativen System mit n Freiheitsgraden nur die Energie erhalten (und E bzw. En somit die einzige Quantenzahl). In diesem Fall verlaufen die Trajektorien in einen
(2n − 1)-dimensionalen Unterraum. Dies kann schon in zweidimensionalen Billiardsystemen der Fall sein:
Der Phasenraum ist zunächst 4-dimensional (2 Orts- und 2 Impulskoordinaten) und wird durch jede Erhaltungsgröße um 1 erniedrigt. In chaotischen Billards ist der Phasenraum somit 3-dimensional, im integrablen
Fall 2-dimensional. Auch chaotische Systeme besitzen periodische Orbits, die sich im Fall der Billardsysteme
recht leicht finden und vorstellen lassen.
....................................
.......
.....
.....
....
...
...
.
.
.
...
...
...
..
.
...
..
....
..
..
...
...
...
..
.
.
...
.
.
...
...
...
..
....
...
......
......
.......
.................................
@
I
@
r
(a)
.............
........
......
...
...
.
...
..
...
....
...
...
...
...
...
....
......
........
............
r
...............
.......
.....
....
...
...
...
..
..
...
.
...
..
.
.
.
.
...
...
.....
.......
................
@
@
R
@
(b)
....................................
..............
.........
.......
.........
......
.......
......
......
.
.
.
.
.....
...
.
.
.
.....
.
...
....
.
.
.
...
...
.
.
...
..
.
...
.
...
...
.
....
...
...
...
...
...
...
.
....
..
.
.
...
....
.....
....
......
.....
......
......
.......
......
.
.
.
........
.
.
.
............
.....
............................................
r
(c)
Abbildung 2: Beispiele von nichtintegrablen Quantenbillards: (a) das Sinai-Billard, (b) das Stadionbillard, (c) das
Zitronenbillard.
P
Die Zustandsdichte ρ(E) = i δ(E − Ei ) und damit auch die Energieniveaus von beiden Systemen (integrable und chaotische) lassen sich über die Spurformel von Gutzwiller finden. Hierzu zerlegt man die
Zustandsdichte in einen glatten und einen oszillierenden Teil,
ρ(E) = ρ0 (E) + ρosc (E).
Während der glatte Teil sehr leicht zu finden ist (er hängt nur von den geometrischen Grössen des Systems
ab), erhält man den oszillierenden Teil aus den periodischen Orbits (r zählt die verschiedenen periodischen
Orbits einschließlich der Wiederholungen)
1 X
νr π
(Tp )r
1
ρosc (E) =
.
(11)
S
(E)
−
cos
r
πh̄ r ||Mr − 1||1/2
h̄
2
H
mit S(E) = pdq, Tp gibt die Umlaufzeit der Orbits an (proportional zur Länge), M̂r ist die sogenannte
”Stabilitätsmatrix” und νr der entsprechende Maslov-Index. Die Herleitung der Spurformel erfolgt durch
das Pfadintegral.
Traditionell wird die Spurformel zwar oft nur im Zusammenhang mit chaotischen Systemen erwähnt, praktisch jedoch lässt sich eine analoge Formel auch in integrablen Systemen (sowie verschiedenen Zwischenfällen
zwischen integrabel und chaotisch) finden.
3.3
Energieniveaus und Niveaustatistik
Schon bevor man die Spurformel kannte, war es aufgefallen, dass viele Serien von Zahlen Ei ganz bestimmte
Verteilungen bezüglich ihrer Abstände
Ei+1 − Ei
si =
∆E
7
besitzen (∆E bezeichnet den mittleren Abstand), z.B. Serien von
• Kernspektren
• Verteilung der Primzahlen
• Nullstellen der Riemannschen ζ-Funktion
• Energieniveaus von Quantenbillards
• Energieniveaus schwingender Quarzblöcke
• Energieniveaus schwingender Aluminiumplatten und Mikrowellenbillards
• Mesoskopische Strukturen (Quantendot-Billards)
• Eigenwerte zufälliger Matritzen
• Zufallszahlen
Die Verteilung P (s) der (normierten) Abstände zwischen 2 aufeinanderfolgenden Niveaus beträgt entweder:
PP (s) = exp[−s] (reguläre Systeme)
oder
PW (s) =
πs2
π
s exp[−
] (chaotische Systeme)
2
4
Dies führte 1984 zur Vermutung von Bohigas, Giannoni und Schmidt” zur Universalität aller Systeme mit
Zeitumkehrinvarianz:
• Die qm Abstandsverteilungen aller Systeme, die sich klassisch chaotisch verhalten, ist Wignerverteilt.
• Die qm Abstandsverteilungen aller Systeme, die sich klassisch regulär verhalten, ist Poisson-verteilt.
• Universalität: Dies hängt nicht von der Größe der Systeme ab, oder von der Anzahl ihrer Freiheitsgrade, sondern nur davon, ob ihre klassische Geometrie chaotisch oder regulär ist.
Diese Vermutung ist inzwischen gut erhärtet, wobei man allerdings auch intermediäre Systeme gefunden
hat. Auch bei reinen Zahlenfolgen kann man die Universalität ganz gut verstehen. So ist z.B. die PoissonVerteilung die Verteilung unkorrelierter Zufallszahlen. Auch die Primzahlen sind näherungsweise Poissonverteilt.
En
En
1
P(s)
140
140
0.8
0.6
120
120
0.4
0.2
0
100
100
0
1
2
s
3
Abbildung 3: (a) Beispiel für Wigner-verteilte Eigenwerte. (b) Beispiel für Poisson-verteilte Eigenwerte. (c) P (s)
gegen s für die Poisson (gestrichelte Linie) und die Wigner-Verteilung (durchgezogene Linie).
8