Übergang: klassische Mechanik → Quantenmechanik

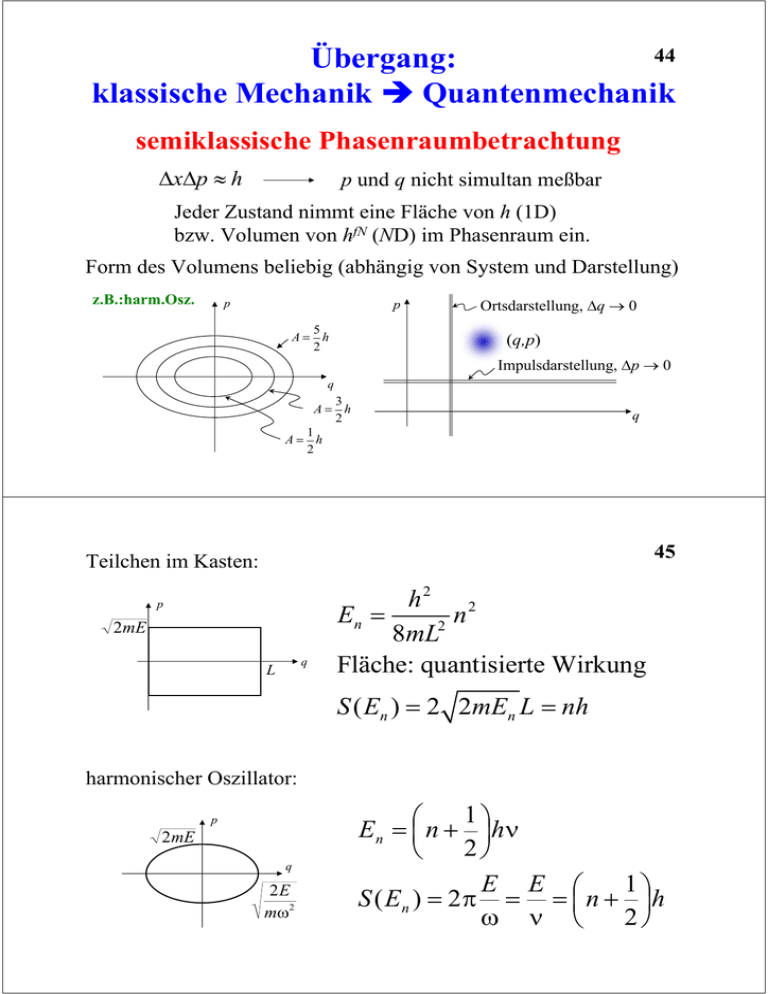
44
Übergang:
klassische Mechanik Î Quantenmechanik
semiklassische Phasenraumbetrachtung
∆x∆p ≈ h
p und q nicht simultan meßbar
Jeder Zustand nimmt eine Fläche von h (1D)
bzw. Volumen von hfN (ND) im Phasenraum ein.
Form des Volumens beliebig (abhängig von System und Darstellung)
z.B.:harm.Osz.
p
p
5
A= h
2
Ortsdarstellung, ∆q → 0
(q,p)
Impulsdarstellung, ∆p → 0
q
3
A= h
2
q
1
A= h
2
45
Teilchen im Kasten:
p
2mE
q
L
h2 2
En =
n
2
8mL
Fläche: quantisierte Wirkung
S ( En ) = 2 2mEn L = nh
harmonischer Oszillator:
p
2mE
q
2E
mω2
1
En = ⎛⎜ n + ⎟⎞hν
2⎠
⎝
E E ⎛
1⎞
S ( En ) = 2π = = ⎜ n + ⎟ h
ω ν ⎝
2⎠
46
Übergang von der Fläche im Phasenraum auf
die Anzahl möglicher Quantenzustände:
1 Teilchen, 1 Dimension:
A Fläche im Phasenraum
=
= Anzahl der mögl. Zustände
h Fläche eines Zustands
Verallgemeinerung auf
N Teilchen, f Dimensionen:
Ω
N !h fN
→ Anzahl der möglichen Zustände
Ω ... Volumen im Phasenraum
hfN ... Volumen der „Einheitszelle“
N! ... Korrektur für Ununterscheidbarkeit
Korrespondenz
klassische Mechanik
Quantenmechanik
aqG , pG f im Phasenraum
i
ψ i im Hilbertraum
i
Observable A ist eine reelle
G G
Funktion von qi , pi
G G
Phasenraumdichte ρ qi , pi
a
f
a
47
f
Ensemble-Erwartungswerte:
z
A = Aρ d 3 N qd 3 N p
Observable A beschrieben durch
selbstadjungierten Operator A = A*
Dichtematrix (-operator) ρ
a f
A = Sp ρA
Γ
Zeitentwicklung, Liouville-Gl.:
d
A = − H, A
dt
d
ρ = + H, ρ
dt
k p
k p
Liouville-von Neumann-Gleichung:
d
i= A = − H , A
dt
d
i= ρ = + H , ρ
dt
→ Berechnung eines Ensemblemittels (statistisches Mittel)
48
O = ∑ ψ (i ) O ψ (i ) pi
i
= ∑∑ On ' n cn(i ) cn( i')* pi = ∑ On ' n ρ nn '
i
Dichtematrix:
n,n '
n,n '
ρ nn ' = ∑ i cn(i ) cn(i' )* pi
→ Ensemblemittel über Bilinearform
Ensemblemittelwert:
O = Sp(Oρ )
Zusammenfassung (siehe QT II):
Eigenschaften der Dichtematrix
a) Hermitizität:
49
ρ n ,n ' = ρ n*',n
b) Nichtdiagonalelemente gehorchen
der Cauchy-Schwartz-Ungleichung:
2
ρ n ,n ' ≤ ρ n ,n ⋅ ρ n ',n '
c) ρ kann diagonalisiert werden
ρ k ,k = ∑k k Pk k ;
d) Normierung:
k = ∑ n an n
Sp ( ρ ) = Sp ( ρ 1) = 1 = 1
e) das Eigenwertspektrum ist positiv definit:
0 ≤ Pk ≤ 1
f) Interpretation der Eigenwerte Pk von ρ:
Wahrscheinlichkeit, System in Eigenzustand k zu finden.
(Eigenzustand von ρ, nicht von H!)
g)
50
Sp ( ρ 2 ) ≤ Sp ( ρ ) = 1 (folgt aus e)
h) statistischer Erwartungswert für beliebigen Zustand
Pn = Sp ( ρ n n ) ;
n n ... Projektionsoperator
i) Zeitentwicklung von ρ ist gegeben durch
Liouville-von Neumann-Gleichung:
i=∂ t ρ (t ) = [ H , ρ ]
j) Dichtematrix eines stationären Zustandes:
[H , ρ ] = 0
⇒ ρ = ρ (H )
k) im stationären Zustand ist die Dichtematrix diagonal in der
Energiedarstellung
51
Quanten-Ergodenhypothese
Zeitmittelwert:
ρ nm = cn (t )cm* (t )
T
= δ nm cn2
T
= ρ nn = P0
Ensemblemittelwert:
M
ρ nm = ∑ c c
i =1
( i ) ( i )*
n m
M
pi = δ nm ∑ cn( i ) pi
i =1
2
52
Brücke zwischen ρ und ρ̂ :
qm
cl
Quanten-Phasenraumverteilung ρW (r, p) (Wignerfunktion):
spezielle Darstellung der Dichtematrix
Forderungen (in Analogie zur klassischen Mechanik):
• Erwartungswert:
G G
G G
G G
A(r , p ) = ∫∫ d 3 rd 3 p ρW (r , p ) A(r , p )
• ρW ist reellwertig
• reduzierte Dichten:
G
G
G
G
G G
ρ (r ) = φ (r ) = ∫ d 3 p ρW (r , p )
2
G G
ρ ( p) = φ ( p ) = ∫ d 3r ρW (r , p)
2
53
Bestimmung von ρW:
Fouriertransformierte der Dichtematrix
a) für reinen Zustand Ψ:
G G
ρW (r0 , p0 ) =
G G
1
G G
G
ip0 r / =
3
* G
d
r
e
ψ
r
−
r
ψ
r
+
r
(
/
2)
(
/ 2)
0
0
3 ∫
(2π =)
G G
G G
r0 − r / 2 ψ ψ r0 + r / 2
b) Verallgemeinerung für gemischten Zustand:
G G
ρW (r0 , p0 ) =
G G
1
G
G G
ip0 r / = G
3
ˆ
d
r
e
r
−
r
ρ
r
/
2
0
0 +r /2
3 ∫
(2π =)
Nebendiagonalelement in Ortsdarstellung
54
Eigenschaften von ρW:
• ρW ist reellwertig
G
G
• liefert korrekte reduzierte Dichten ρ ( r ), ρ ( p )
• Wignerfunktionen sind orthogonal, wenn die
zugrundeliegenden Zustände orthogonal sind
G 3 G ψ1 G G ψ 2 G G
d
r
∫ 0 ∫ d p0 ρW (r0 , p0 ) ρW (r0 , p0 ) =
3
1
ψ1 ψ 2
3
(2π=)
1
→
h Nf
2
G 3G ψ G G 2 1
⇒ ∫ d r0 ∫ d p0 ρW (r0 , p0 ) = 3
h
G G
1
⇒ ρWψ (r0 , p0 ) ≤ 3 ⇒ maximale Phasenraumdichte:
h
1 Zustand pro Quantenelementarzelle
3
55
G G
1
ρW (r0 , p0 ) < Nf
h
G G
ψ
ρWψ (r0 , p0 ) =
p
1
h Nf
p
q
q
konzeptionelle Schwierigkeit der Wignerfunktion:
56
ρW ist nicht positiv definit
daher Interpretation von ρW als Phasenraumdichte des
G G
Zustandes ψ am Punkt ( r0 , p0 ) problematisch
Konstruktion einer positiv definiten Dichte durch
Mittelung über ein Gauss‘sches Wellenpaket minimaler
Unschärfe („grobkörnige Mittelung“)
⇒ Husimifunktion
G G
ρ H (r0 , p0 ) =
G G 2
⎡
G
G
− p0 ) σ 2 G G 2 ⎤
(
p
1
3
3
(r − r0 ) ⎥
−
d r ∫ d p ρW (r , p ) exp ⎢−
2
σ
(π= ) 3 ∫
=
=
⎣
⎦